基于众包的外卖配送订单选择研究

戴 韬，沈 静

(东华大学 旭日工商管理学院，上海 200051)

外卖配送是外卖O2O中重要的服务环节，外卖平台为了提升竞争力，保证较高的服务质量和用户体验，纷纷建立基于众包的配送平台，如蜂鸟众包、美团众包等。众包模式的引入，既解决了平台自建物流配送模式中固定的配送员运力与波动的订单量不匹配的问题，也为临时配送员兼职服务提供可能。

外卖配送主要有3种订单分配方式：派单、抢单和抢派结合。对于参与众包的兼职配送员来说，工作时间更灵活，抢单的自主选择性更强。在抢单模式下，外卖平台以取餐点与配送员位置等指标向附近配送员推荐一批订单，配送员抢单成功则必须完成该订单。而众包配送员在选择订单时往往凭经验与下意识的反应，若接受不适合的订单容易导致送餐延误产生赔付、客户投诉等情况，既影响众包配送员的收益，降低其参与众包的积极性，又影响外卖平台的服务声誉。

因此，本文从配送员的角度出发，对众包模式下的外卖配送订单选择问题进行研究，提出基于路径规划的双层算法，通过比较接受不同订单所带来收益进行订单选择，使得在满足各项约束下配送员的实际所得收益最优。本文的研究结果能提高众包配送员的工作效率及收益，也能提高外卖平台的订单推荐效率。

1 相关文献综述

订单选择是从大量任务中选择最适合的若干个任务进行执行，也被称为任务推荐，不少学者为众包模式下的任务推荐提供了多种解决思路。Azi等[1]对空间众包下实现工人收益最大的在线配送路径进行研究，在此基础上为动态任务推荐提供参考，文中采用自适应大型邻域搜索启发式算法求解。Sun等[2]同样关注了该问题，不同的是采用基于预测的路径推荐算法进行任务推荐。Deng等[3]提出基于动态编程和分支定界策略的精确算法，用于求解时空众包模式下，单个工人完成任务数最多的任务推荐问题。邓娜等[4]采用基于聚类分析和TSP路径规划的外卖配送订单集指派模式，以配送距离最短为原则将配送员和订单匹配。宋天舒等[5]将众包任务地点也作为考虑因素，提出自适应随机阈值算法进行任务内容、众包人员和任务地点的三维匹配，使得总效用最大。

外卖配送及众包物流的路径规划成为近几年的研究热点之一。李桃迎等[6]对动态外卖订单调度及配送路径问题进行研究，提出基于商家和顾客聚类的路径规划。蒋丽等[7]在对众包外卖配送路径规划的研究中，提出加入未来潜在客户数量影响因子的蚁群算法，使得配送成本最小。吴腾宇等[8]针对O2O外卖配送中需求不确定及取送货的特点，建立相应的路径规划模型，设计了TAIB算法和IGNORE算法，实现外卖配送车辆的实时调度。慕静等[9]基于众包物流参与人员积极性不高等问题，以最大化收益为目标，构建众包物流运力调度问题模型。陈萍等[10]提出基于时间满意度的外卖配送路径优化模型，并使用改进的遗传算法求解。Liu等[11]构建一个纳入出租车众包配送的外卖配送网络，采用包括构造算法和大邻域搜索算法的两阶段方法解决配送问题，使得所需出租车数量最少。Veenstra等[12]研究包含取送货按后进先出处理成本的取送货旅行商问题，基于此特点建立模型，并采用大邻域搜索算法求解。

外卖配送路径规划与取送货旅行商问题(pickup and delivery travelling salesman problem, PDTSP)比较接近。由于VRP问题为NP难问题，因此通常使用启发式算法求解，主流的有遗传算法、蚁群算法、禁忌搜索算法和粒子群算法等。Zhao等[13]提出一种混合遗传算法，用于解决取送货一体的旅行商问题。潘立军等[14]在传统遗传算法的基础上，采用时差插入法改进交叉算子、变异算子与变异算子的设置，并使用非代际搜索策略求解带时间窗取送货问题。Ai等[15]提出一种基于随机密钥解决方案的粒子群算法，用于实现取送货车辆路径问题，基于客户优先级列表和车辆优先级矩阵构建车辆路线。

综上，任务匹配与取送货一体化TSP问题的先期研究为本文奠定了很好的理论基础，但是本文研究的配送订单选择问题是一个“开放性”的决策问题，配送员可以根据自身情况选择一个或多个备选订单；在执行一系列订单过程中，与TSP问题不同，具有“路径开放(不用回到起点)”、“参与时间有限”、“最终目的地确定”等特点。这些特点让问题变得更加复杂，因此本文提出将订单选择与执行路径统一考虑的双层算法。

2 决策模型与算法

2.1 问题描述

外卖配送订单选择的实际场景为众包配送员在尚有未完成的待配送订单情况下，如何从系统推荐订单列表中选择多个订单，使得配送收益最大化的问题。可以抽象描述为配送员在 T时刻前到达某个指定点，在此之前可参与兼职配送，现有 m个订单尚未配送(可能部分已取)。此时外卖平台的配送订单推荐列表中有 n个订单可供配送员进行抢单，配送员如何从列表中选择合适的订单，使得完成所有订单后按时到达终点，同时配送收益最大化。

2.2 双层算法逻辑与说明

由于外卖配送的所得收益不仅是订单配送费用的简单相加，还需扣除因延迟配送导致的惩罚，因此在选择订单时需考虑是否能在规定时间内送达、是否会产生惩罚等情况。配送路径规划本身是NP难问题，订单选择是基于配送路径规划的更高层次的决策问题，而且由于现实问题的特点，模型的求解速度要求较高，更加大了决策难度。

本文提出双层算法基本逻辑是上层逻辑为贪心算法，即通过某个评分机制，对待选择订单进行评分。由于平台实时推荐的订单数量较多，为了提高求解速度，将根据评分结果筛选出分数较高的 n个订单进入考虑选择的范围，由大到小逐个加入这n个订单进行配送路径规划，并得到相应的配送收益，若加入新订单后的配送收益大于配送原有订单所带来的收益，则接受该订单，否则，不接受，直到再加入新订单无法得到可行解；下层逻辑为以配送收益最大为目标的考虑时间窗、延迟配送惩罚、配送携带订单数量约束等现实因素的配送路径规划模型，对应的求解算法是改进的遗传算法。

双层算法流程如图1所示。

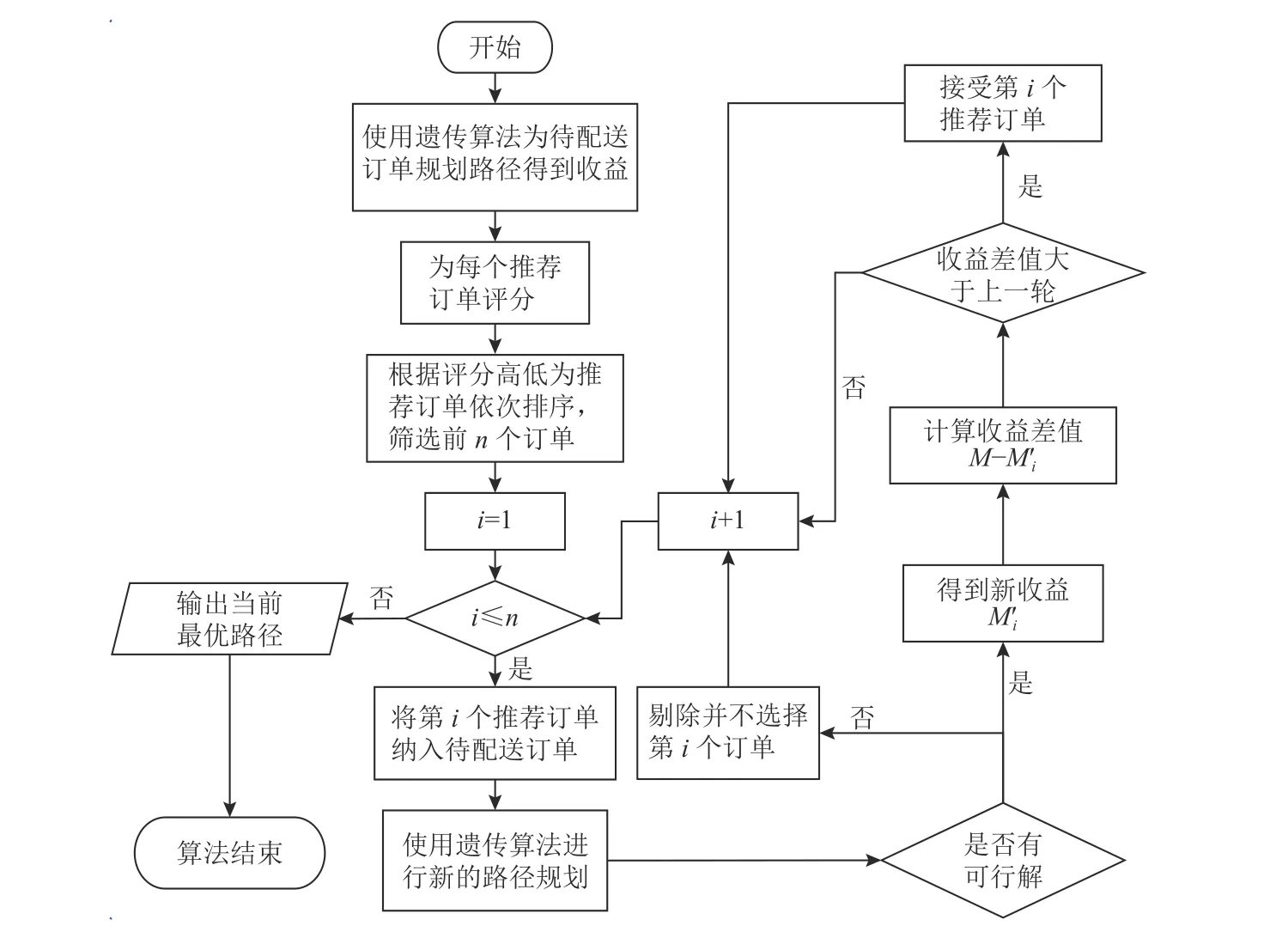
图1 双层嵌套算法逻辑图Figure 1 The logic diagram of two-layer algorithm

2.3 订单评分模型

在上层算法中，依次加入推荐订单的顺序将直接影响最终订单选择的结果，而 n个订单所有可能的顺序组合有种。为了减小求解规模，同时增加较优的订单被选择的可能性，本文建立订单评分模型，根据分数高低确定订单加入的顺序与规模。

本文考虑影响配送订单选择的主要因素包括订单配送费、订单服务点(取餐点或送餐点)与待访问点(待配送订单的取餐点或送餐点)间的距离、送餐点与配送员计划终点的距离、取送餐方向。针对上述4个主要因素构建评分模型为

其中， s(FR)i为基础配送收益，本文将用订单i的配送费占推荐列表中所有订单配送费总和的占比表示； s(PDN)i、 s(DDN)i为订单i的取餐点、送餐点与原计划下一访问点间的距离得分，距离越近分数越高； s(DDR)i为 订单i送餐点与计划终点间距离得分，计算方法与 s(PDN)i以 及 s(DDN)i相同； s(DR)i是取送餐方向得分，订单i的取餐点或送餐点若在配送员当前位置至计划终点的方向相反的区域，则该项得分为0，反之为1。 FW、 N W、 D DW、 D W分别表示各因素所占权重。

2.4 众包外卖配送路径规划模型

外卖配送有以下几个特征：1) 每个订单需先取餐再送餐；2) 取餐及送餐均有时间窗；3) 因为保温箱容量有限，有携带订单数量限制。除此之外，众包(兼职)配送员可以在任意空闲时间开始或停止接单，因此，众包配送员的配送路线一般不是闭环：从当前位置开始配送，完成所有任务后在某个最晚时间前回到一个预期的终点，如图2所示。配送电动车受电瓶电量限制有行驶里程约束，全职配送员一般会配备多个电瓶克服里程限制。而众包配送员多为兼职参与，因此需考虑电动车电量所能支持的行驶里程。综上，在前3个基本特征之外，众包配送新增的特征为：4) 开放式取送货旅行商问题；5) 有最晚到达终点时间约束；6) 有行驶里程约束。

2.4.1 问题描述及模型假设

考虑 n个 配送任务时，配送网络包含1个配送员当前位置、1个配送员计划终点和 2n个服务点(取送餐)，配送员须在时间 T前完成所接受的配送任务并回到计划终点。定义网络中节点集合V={0,2n+1}∪R∪C， 其中，节点 0表 示当前位置；节点 2n+1表示终点；集合 R={1,2,···,n}表示所有订单的取餐点；集合 C ={n+1,n+2,···,2n}表示所有订单的送餐点；i和 n +i分 别对应订单i的取餐点和送餐点。配送员将决策收益最大的配送路径，要满足的约束有：须在每个节点的时间窗内访问该节点；若超出最晚送餐时间则产生延时惩罚；同时每个订单必须“先取再送”；配送过程中携带的订单数有限；时间 T前到达计划终点。

本文假设如下。1) 配送员在取餐和送餐过程中的服务时间忽略；2) 车辆在行驶过程中行驶速度确定；3) 行驶成本与行驶路径成正比；4) 对于超时送餐的订单，将取消配送费，并惩罚一倍配送费的金额。

2.4.2 参数说明及数学模型

1) 符号定义。

O：所有订单集合。

2) 模型参数。

①车辆相关参数。

v为车辆行驶速度； Q为车辆携带订单容量；L为最大里程限制； α为行驶成本系数。

②网络图相关参数

dij为 节点i到 节点 j 的距离； ai为 车辆 到达节点i的时间； si为 车辆离开节点i的 时间； wi为车辆在节点i的等待时间；qi为 车辆离开节点i时所载订单数量。

③订单参数。

3) 决策变量。

根据上述定义，得到配送路径模型为

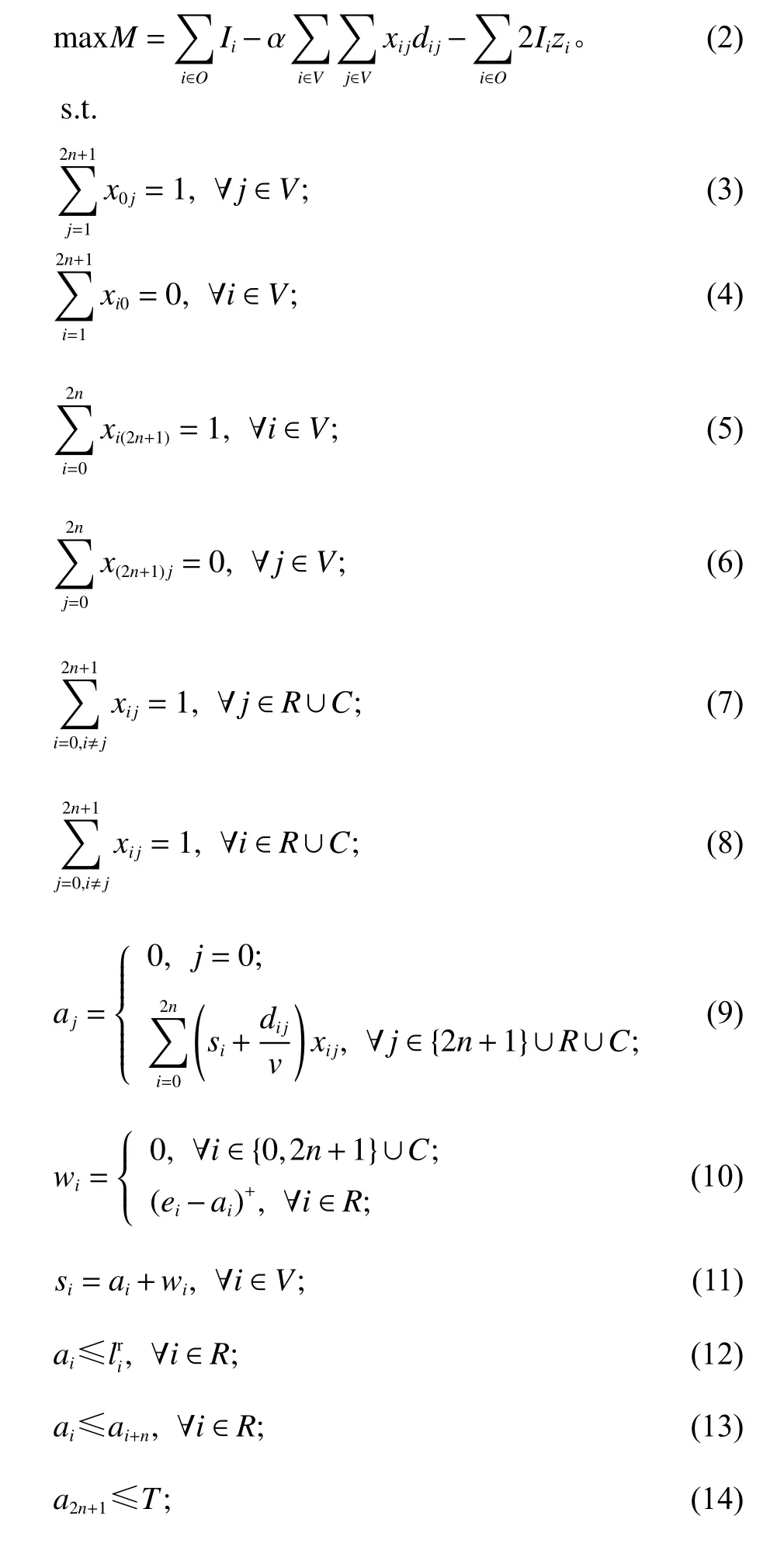
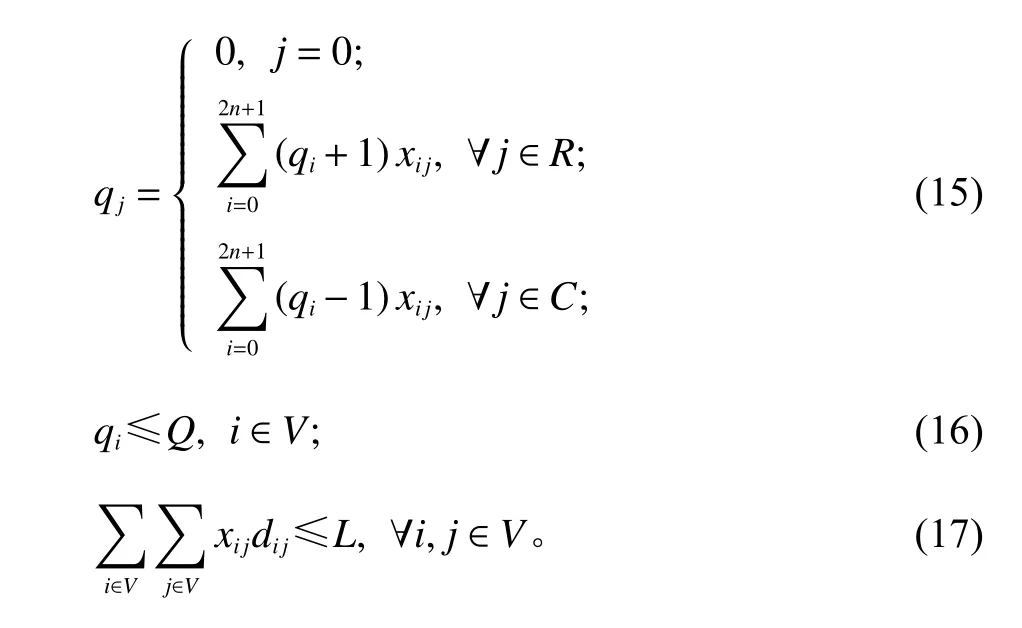
其中，式(2)为目标函数，表示配送收益最大化；式(3)、(4)表示配送员从当前位置节点0出发；式(5)、(6)表示配送员最后回到计划终点；式(7)、(8)表示每一个订单的取餐点和送餐点都必须被访问一次；式(9)计算车辆到达节点 j的时间；式(10)、(11)为配送员在节点i的等待时间以及离开该点的时间；式(12)保证最晚取餐时间被满足；式(13)确保先取餐点后送餐点；式(14)表示配送员在预期时间内完成待配送任务并到达终点；式(15)、(16)为车辆携带订单数量约束；式(17)保证配送行驶路程不超过当前电动车剩余电量所能满足的里程。

2.5 改进遗传算法设计

1) 编码方式。

为了便于体现取餐点和送餐点的区别，本文采用自然数编码的方式对取餐点和送餐点进行编码，0,1,2, ···,2n+1表示2n+2个访问点，其中，0为起点，1,2,…,n为取餐点，分别对应第1,2, ···,n号订单，送餐点对应为n+1, n+2, ···, 2n，终点为2n+1，即订单 i的取餐点编码为i，送餐点为 i +n。例如，假设当前有5个待配送订单，取餐点和送餐点编码如表1所示，起点为0，终点编码为11。以上编码组随机排序组合成一条染色体，代表一条配送路线，如0-2-1-6-4-7-3-8-5-10-9-11，其中，每个编码代表染色体上的一个基因。

表1 5个待配送订单的取餐点及送餐点编码Table 1 Serial ID of 5 orders pickup and delivery nodes

2) 初始化种群及改进的个体构造方法。

由于带有取送餐顺序约束以及携带订单数量约束，随机生成的初始种群符合约束的概率较小，遗传难以进行下去。为了提高初始种群的质量以及算法运算速度，本文提出2个构造方法在随机生成初始种群的基础上，对不符合约束的染色体重新构造。

① 取送餐顺序约束构造。

若随机生成的染色体中存在某个送餐点在对应订单的取餐点之前访问，则将该订单的取餐点移到送餐点前一位，送餐点与原取餐点位置中间的访问点依次后移一位。例如，当前有5个待配送订单，假设随机生成的某一染色体为0-2-3-4-6-7-8-1-9-5-10-11，其中，1号订单的取餐点1出现在对应的送餐点6之后，不符合取送餐顺序约束，因此将基因1移至基因6前一位，原染色体中基因6与1之间的基因依次后移一位，其余基因位置保持不变，形成新的染色体，其操作如图3所示。

图3 取送餐顺序约束调整操作图Figure 3 Examplefor sequence constraint adjustment

② 携带订单数量约束构造。

配送员在访问取餐点后车辆携带订单数量加1，访问送餐点后数量减1。若在访问某点后，车辆携带订单数量超过容量，那么该点一定为取餐点，同时，该取餐点前一定有其他尚未送餐的订单的取餐点。因此，为了避免破坏取送顺序约束，本文以该取餐点所在的基因位为界限，从该取餐点之后的基因中选取已经取餐但尚未送餐订单的送餐点，将该送餐点前移。以图4为例，假设车辆携带订单容量为2，车辆访问取餐点4后订单数量为3，超过容量限制，因此从取餐点4往后寻找已经在该点之前取过餐的订单对应的送餐点，先找到送餐点7，将7移至4前一位，原染色体中4与7之间的基因均依次后移一位，其余基因位置保持不变，形成新的染色体。

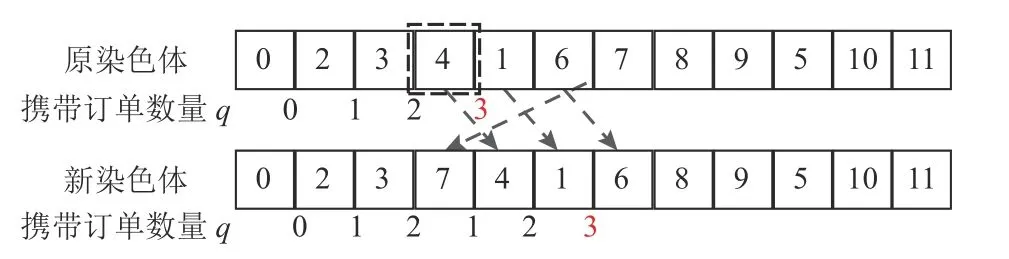
图4 携带订单数量约束调整操作图Figure 4 Example for order amount constraint adjustment

经过一次调整可以得到新染色体，但该染色体仍有可能违反约束，例如取餐点1。因此，需要按照上述方式进行顺序检查，最后可以得到如图5所示的符合约束的可行解。

图5 经过调整后满足约束的染色体Figure 5 A feasible chromosome after adjustment operations

3) 适应度函数。

模型适应度函数与目标函数一致，适应度函数f =M。若染色体不满足最大里程约束或者最晚到达终点时间约束，则该染色体的适应度直接计为0。

4) 遗传算子设计。

① 采用轮盘赌方法选择算子。

② 使用双交叉点法选择交叉算子，即随机选取2个基因点，获取父代染色体中在基因点之间的基因片段，并将这2个基因片段互换，形成2个新个体。例如，如图6所示，2条父代染色体随机选取的交叉点为4和7，则交叉的基因片段为“4-8-1-6”和“1-6-5-8”，将这2段基因片段在父代染色体中互换，得到新的子代染色体。可见，子代1中取餐点5重复出现，却缺少取餐点4，子代2中取餐点4出现2次，却缺少取餐点5，说明交叉得到的染色体很容易不符合约束。

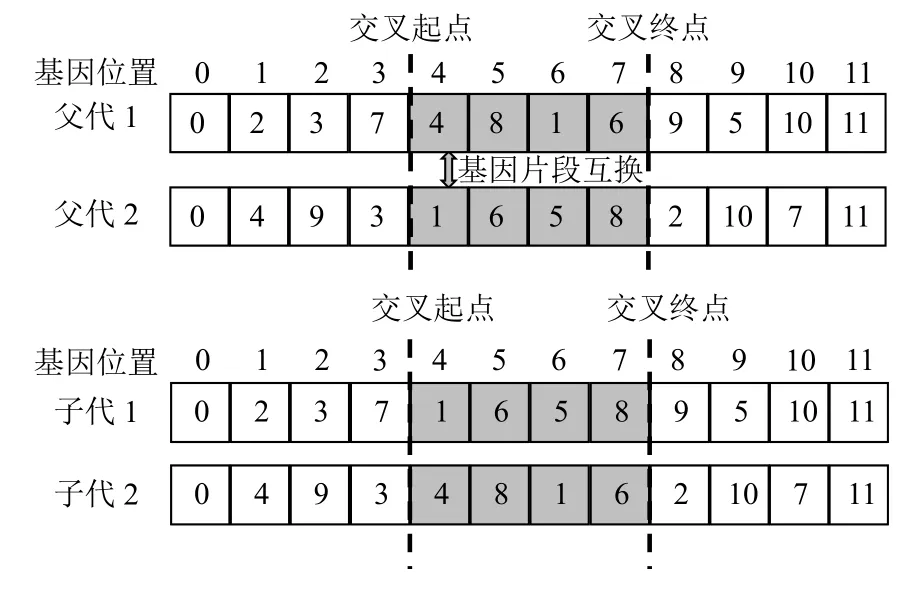
图6 父代染色体交叉Figure 6 Chromosomes crossover

为了解决交叉操作后基因重复问题，本文的处理是先找出交叉片段与染色体中的重复基因，子代1的基因5和子代2的基因4，然后进行重复基因互换，如图7所示。同理，若重复基因有多个，则在子代的交叉片段中的基因互换也需要进行多次。

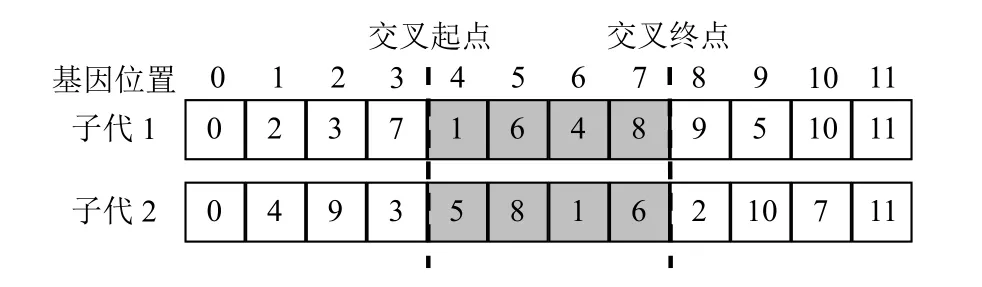
图7 处理重复基因后的子代Figure 7 Offspring after handling duplicate gene

③ 根据变异概率判断父代染色体是否变异，若变异，则随机选择2个基因位置，交换这2个位置的基因，形成新的子代。

④ 本文采用精英选择策略进行种群更新，先进行当前种群的交叉和变异，交叉及变异得到的新的子代若不符合约束，同样使用2)中所述构造方法将其改造，然后根据染色体的适应度从父代和子代群体中筛选出当前适应度最高的染色体，数量满足群体大小，形成新的种群。

5) 遗传终止条件。

为了确保算法尽可能接近最优解，同时减少运算时间，采用以下2个迭代终止条件：① 若连续100次迭代的适应度相同，则终止迭代；② 迭代次数达到最高次数1 000次，则终止迭代。

3 算例实验

3.1 算例基础数据

假设某众包配送员当前位置为(0,0)，计划在1.2 h后到达终点为(2,2)，尚有 3个订单未配送，待配送外卖订单信息如表2所示。此时外卖平台根据就近取餐原则，向该众包配送员推荐了若干个新订单，根据表3所示的权重设置为订单打分，假设从其中分数最高的10个订单中进行选择，纳入考虑选择范围的10个订单信息如表4所示。

表2 待配送外卖订单信息Table 2 Order info.in to-do list

表3 订单评分模型权重设置Table 3 Weight setting in order scoring model

表4 备选外卖配送订单信息Table 4 Alternate delivery order info.

对配送过程及配送车辆的各项参数设置以及订单评分模型权重设置分布如表5所示。

表5 车辆及配送服务实验参数设置Table 5 Experimental parameters of vehicle and delivery service

3.2 算例实验结果

本文使用C++语言在Visual Studio 2017中编写程序并运行，实验运行环境均为Intel Celeron i5-1017U 1.60 GHz CPU，6GB内存和Windows 10专业版64位操作系统。遗传算法的参数设定为种群大小=100，交叉概率=0.7，变异概率=0.1。

当前待配送订单的路径规划结果如表6所示，最优配送路径为“0→2→1→3→4→5→6→7”，当前配送收益为18.22元。

在现有3个订单基础上，利用设计的双层算法从10个备选订单中选择最合适的一些订单。为了验证算法的计算速度，进行15次实验，如图8。除了第2次运算时长超过4 s外，其余14次实验所用时间均在3 ～ 4 s之间，运行平均时间为3.67 s，证明从10个备选订单进行选择花费时间可接受。

表6 当前待配送订单配送路径规划结果Table 6 Delivery route planning for current orders

图8 基础算例15次实验运算时间Figure 8 Calculating time of 15 experiments on basic example

在运行时间验证的基础上，继续进行算法效率验证。图9为15次实验中典型的收敛图，大部分实验均在适应度53左右时收敛。

图9 基础算例典型实验收敛图Figure 9 Typical convergence graphs of basic example

表7和图10更直观地展现了依次加入推荐订单后的配送收益变化。可以看出，并非订单数量越多配送收益越大，若多个订单的送餐时间窗相近，过多的订单将导致送餐时间延迟产生惩罚，进而降低配送收益；此外，初始的订单评分越高只是表示“优先考虑”但并非“最终选择”，如订单7的评分为4.26，订单3的评分为4.15，模型先考虑了订单7，但最后仅选择了订单3，产生这种情况的原因是加入订单7后的配送收益小于订单3。表8展示了配送收益最优的订单选择，加入推荐的9、10、6、4、5、3号订单后收益可达53.06，增加了34.84，配送路径从自然编码翻译成最终结果为起点→取10→送10→取3'→取1'→送3'→送1'→取9→送9→取5→送5→取3→送3→取6→送6→取4→送4→取2'→送2'→计划终点。

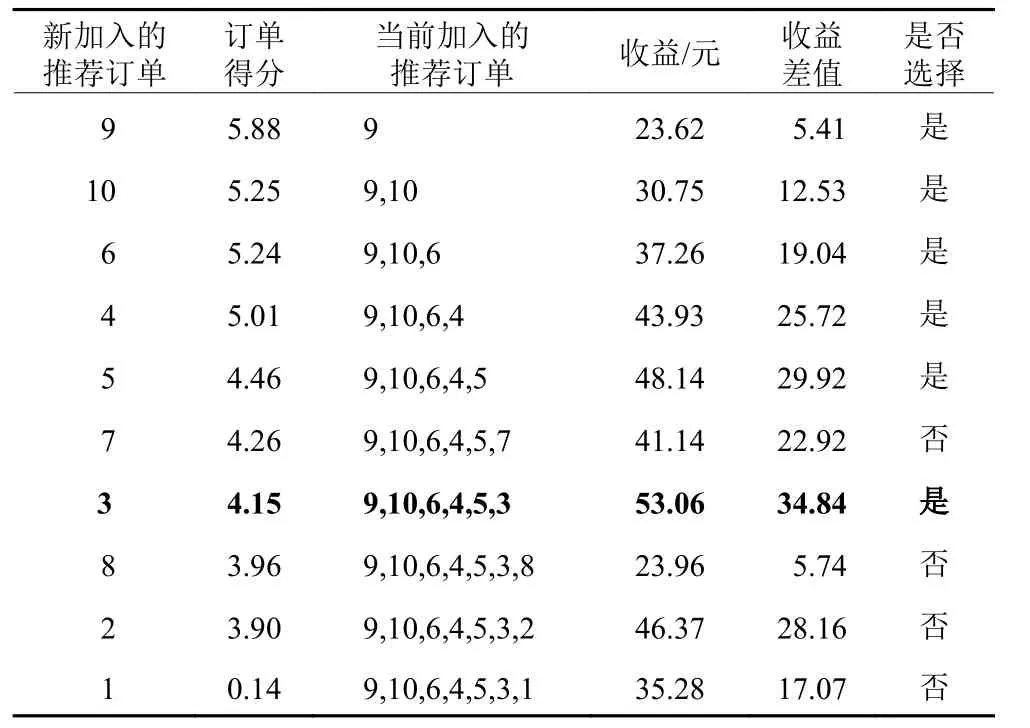
表7 多个推荐配送订单选择计算过程Table 7 Calculation process of multiple recommended delivery order selection

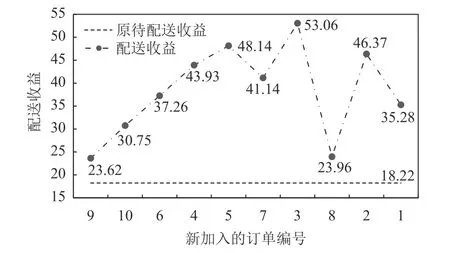
图10 订单选择过程中配送收益变化图Figure 10 Revenue graphwithnewadd-in orders

表8 多个推荐配送订单选择结果Table 8 Result in multiple delivery order selection

此基础上，为了验证算法的稳定性，本文继续设计9组不同推荐规模的算例进行实验，本文认为经过评分排序，现实纳入备选范围的订单数量不会超过20个，因此这9组算例中待配送订单同样为3个，备选订单分别为11～19个，其余参数与表5相同。9组算例在分别经过10次实验后得到平均程序运行时间如图11所示。由此，可以得到以下2个结论。

图11 不同备选订单数量所需平均推荐时间Figure 11 Average calculating time with different numbers of alternate orders

1) 随着选择的推荐订单数量增加，仍然能得到较优推荐结果，程序运算时间随之线性增长。

2) 导致运算时间与推荐订单数量线性相关的原因是，随着订单规模的增大，调用双层算法中下层遗传算法进行迭代的次数增加，因此总运行时间与备选订单数量呈正相关。同时这也说明本文所设计的下层改进遗传算法稳定性较好，单次运算时间不会随着订单数量增加明显改变。

4 结论

本文根据众包配送的特点，提出双层算法为众包配送员在抢单过程中选择订单提供决策参考，其中接受新订单的原则是考虑惩罚后的配送收益最大化。本文将订单选择与路径规划同时考虑，基于订单初始评分决定进入订单选择的次序，再利用整数规划模型决定是否选择该订单并进行下层的路径规划，在路径规划时，允许订单交叉执行。在求解下层的路径规划模型中，本文设计了改进的遗传算法，主要的创新是进行染色体的再构造，实现众包配送必须的取送餐顺序及订单携带数量约束。论文在算例实验中验证了模型与算法在小规模问题下的求解效果与求解速度。在此基础上，发现将本文方法扩展到更大规模的问题时，求解时间是线性增长的。因此对于大规模的现实问题，通过本文提出的打分方法，进行订单的初始筛选和排序是必要的。