考虑网点共享与变更的多级快递网点选址问题

王冰怡，张 锦,2

(西南交通大学 1.交通运输与物流学院；2.综合运输智能化国家地方工程实验室，四川 成都 610031)

根据《2018年中国快递发展指数报告》(下称《报告》)，我国每万人有1.5个快递网点，每百平方公里有2.2个快递网点，各快递企业平均每天服务2.8亿人次，网点密度稠密化发展。快递业务量的增加和企业规模的扩大为城市快递网点的发展带来诸多问题。目前大多数快递企业在城市的网点布局为分拣中心到中转站再到末端网点的三级结构，各快递企业的多级网点较为独立，尚未形成规范管理的城市快递配送节点体系，造成网点重复建设现象，资源利用率较低。除此之外，《报告》显示，目前我国城市已初步形成住宅投递、智能快件箱投递和公共服务站投递等多种模式互为补充的末端投递服务格局，但其模式选取多数未考虑不同区域客户偏好，致使客户对现有快递末端网点所提供的服务模式满意度较低。针对上述现象，快递企业急需充分整合物流资源，优化网点布局，建立更有针对性的多级快递网络。

目前针对多等级或多类型设施选址的研究较少。王海花等[1]在满足客户需求的前提下，基于服务半径对快递柜的选址问题进行研究。陈磊[2]结合宅急送公司网点布局存在的问题，通过快递网点供需状况分析确定应选取的优化模式。韩珣等[3]提出多类型自提点构成的嵌套型多级自提网络结构，建立以顾客效用最大和企业建设成本最小的多级自提点选址模型。周林等[4]建立送货上门与客户自提结合的需求模型，设计包含多容量选址的两阶段模拟退火启发式算法求解。杨朋珏等[5]针对客户的个性化需求，考虑送货上门效率和自提便利性，建立多目标末端网点选址模型。Murali等[6]考虑覆盖函数和需求的不确定性，采用启发式算法对城市多级设施选址问题进行求解。

学者对于物流配送网点的研究主要集中于模式优化、布局规划等方面。韩珣等[7]针对末端自提点通过信号强度函数和概率函数，刻画联合覆盖对顾客选择的影响，建立竞争环境下自提点选址模型。陈绍洵等[8]设计内外层嵌套遗传算法和基于消费者的匹配算法对生鲜自提柜的双层规划模型进行求解。张震等[9]考虑客户需求与商品来源的多元化及商品退货等实际问题，构建考虑退货的多商品多来源闭环选址库存模型。Asl-Najafi等[10]针对动态闭环选址库存问题，以总成本最小和系统时间最短为目标函数，设计基于粒子群优化和快速非支配解排序遗传算法相结合的混合启发式算法进行求解。Hatefi等[11]考虑客户需求的不确定性，提出一种考虑不确定参数和设备故障的双向物流网络综合模型。

综上所述，目前国内外针对单一快递企业网点选址的研究较多，且研究主要集中于物流中心或末端网点选址，对多家快递企业各级网点共享模式下的选址问题研究较少，且网点容量多为定值。本文从网点共享的角度出发，针对快递企业“集散中心−物流中转站−末端网点”的网点布局结构，考虑末端网点服务模式和容量的变更，以系统总成本最小、客户满意度和网点服务效率最优为目标建立多级快递网点选址模型，以期为城市快递网点布局提供参考。

1 问题与模型

1.1 末端网点变更方式

本文涉及到的末端网点变更包括2种类型，分别是末端网点服务模式变更和末端网点容量变更。

1) 服务模式变更。

末端网点主要提供自提柜、代理门店、自有门店3种不同服务模式，每个末端网点仅能提供1种模式。现阶段快递企业在建设末端网点时多数仅从自身角度进行考虑，较少考虑不同区域顾客对于不同服务模式的偏好性。本文将设计算法对现有服务模式进行调整，考虑顾客对不同服务模式的满意度和末端网点服务模式变更为另一种时的建设成本，最终求解得到的多级快递网点选址方案中，末端网点所提供的服务模式可使总成本较低的情况下保证顾客满意度处于较高水平。

2) 网点容量变更。

已确定服务模式的末端网点有其容量限制，在网点共享的情况下，原有末端网点将由单一企业网点变为多家企业共用网点，其原有容量有可能不满足现有需求量。在模型求解时将比较扩大网点容量的扩建成本与新增网点的建设成本的大小，最终确定是否扩建网点、扩建规模。

1.2 问题描述

对本文涉及的多级快递网点选址问题描述如下。如图1所示，某一区域快递配送网络中，有多个不同快递企业的集散中心、中转站、末端网点及众多需求点，末端网点共有自提柜、代理门店、自有门店3种不同服务模式，每个末端网点只能选择1种服务模式，不同的需求点分属于住宅区、商业区、学校区、工业产业区四大不同类型区域。已知各需求点所属区域、位置和需求量，给出若干中转站备选点和不同服务模式的末端备选点，帮助参与企业决策中转站和末端网点的数量、服务模式和位置，提升快递资源利用率。模型拟解决的关键问题如下。

1) 中转站、末端网点选址；

2) 中转站−末端网点、末端网点−客户的服务关系分配；

3) 被选中的末端网点服务模式确定；

4) 被选中的末端网点改、扩建需求及规模确定。

不失一般性，对本问题作如下假设。

1) 末端网点不提供送货上门服务，即所有模式的末端网点均为自提点；

2) 不同类型区域内开设同种服务模式末端网点，其初始容量相同，若所选末端网点不能满足所有客户需求，可对网点服务模式进行更改或对网点进行扩建；

3) 各相同级别网点间不存在调度问题；

4) 各中转站可至少被一家快递企业的集散中心覆盖。

图1 多级快递网点选址问题示意图Figure 1 Problem description Descriptiom of multi-level express outlets layout

1.3 符号说明

I 为中转站集合，i ∈I；

J为末端网点集合， j ∈J；

K为顾客集合，k ∈K ；

M 为集散中心集合，m ∈M；

N为快递企业集合，n ∈N；

R为 末端网点服务模式集合， R ={1,2,3}，分别代表自提柜、代理门店、自有门店3种模式， r ∈R；

dmi、 dijr、 djrk分别为集散中心到中转站、中转站到末端网点、末端网点到客户的距离；

li、 ljr分别为中转站、末端网点服务半径；

hmi、 hijr分别为集散中心到中转站、中转站到末端网点的单位运费；

pi、 pjr分别为中转站、末端网点的容量；

Dk、 Uk分别为客户对末端网点服务满意度的最小、最大临界距离；

Qk为客户能接受的末端网点服务水平的最不满意程度；

Si、 Sjr分别为满足覆盖范围的中转站、末端网点的集合，其中，Si={i|dijr≤li}， Sjr={jr|djrk≤ljr}；

θ1、 θ2分别为中转站和末端网点最终需要的数量；

xi、 xjr分别为0-1变量，若在i/j设立中转站/末端网点，取1，否则取0；

yijr、 yjrk分别为0-1变量，若中转站i为j配送，j为k 提供第r种服务，取1，否则取0。

1.4 顾客满意度函数与效率函数

1) 满意度函数。

末端网点与客户之间的距离会影响客户接受服务的便利性。设 sljrk为客户点k对末端网点 jr所提供服务的评价，其中，s ljrk∈[0,1]，其和末端网点与客户之间的距离共同决定客户对末端网点的满意程度。通过分段函数刻画客户对末端网点的满意度 f(djrk)为

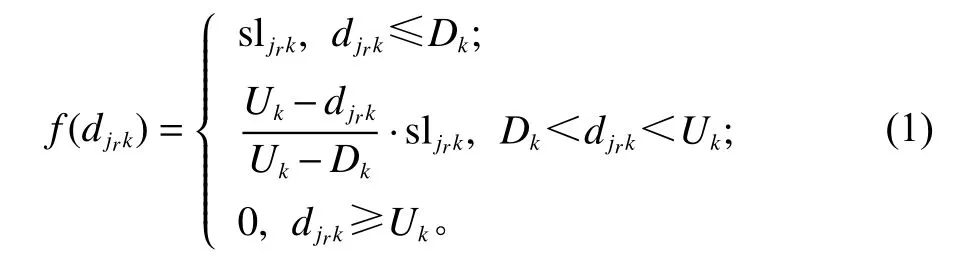
2) 效率函数。

末端网点的布局会影响快递网络运营的效率。因各客户点需求量不同，使末端网点距离需求量大的客户点更近，可以有效提升网点的服务效率。引入客户需求量权重 ωjrk为

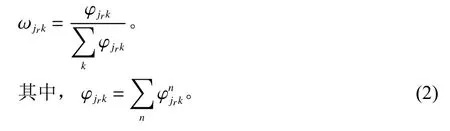
末端网点与客户间的距离和客户需求量共同作用于网点服务效率。结合客户需求量权重，令ωjk=max{ωjrk|∀jr∈Sjr}， 引入效率函数g (djrk)为

1.5 多目标优化模型构建

基于上述分析，构建考虑网点共享的多级快递网点选址模型，考虑不同客户点所属区域、各级网点覆盖范围、各级网点容量对下级的分配、末端网点模式选择等约束条件，以参与企业建设成本、运输成本最小，客户满意度及网点服务效率最高为目标，引入满意度权重系数α1及服务效率权重系数α2，权重取值由决策者偏好决定，其中，α1+α2=1，具体模型及约束条件如下。

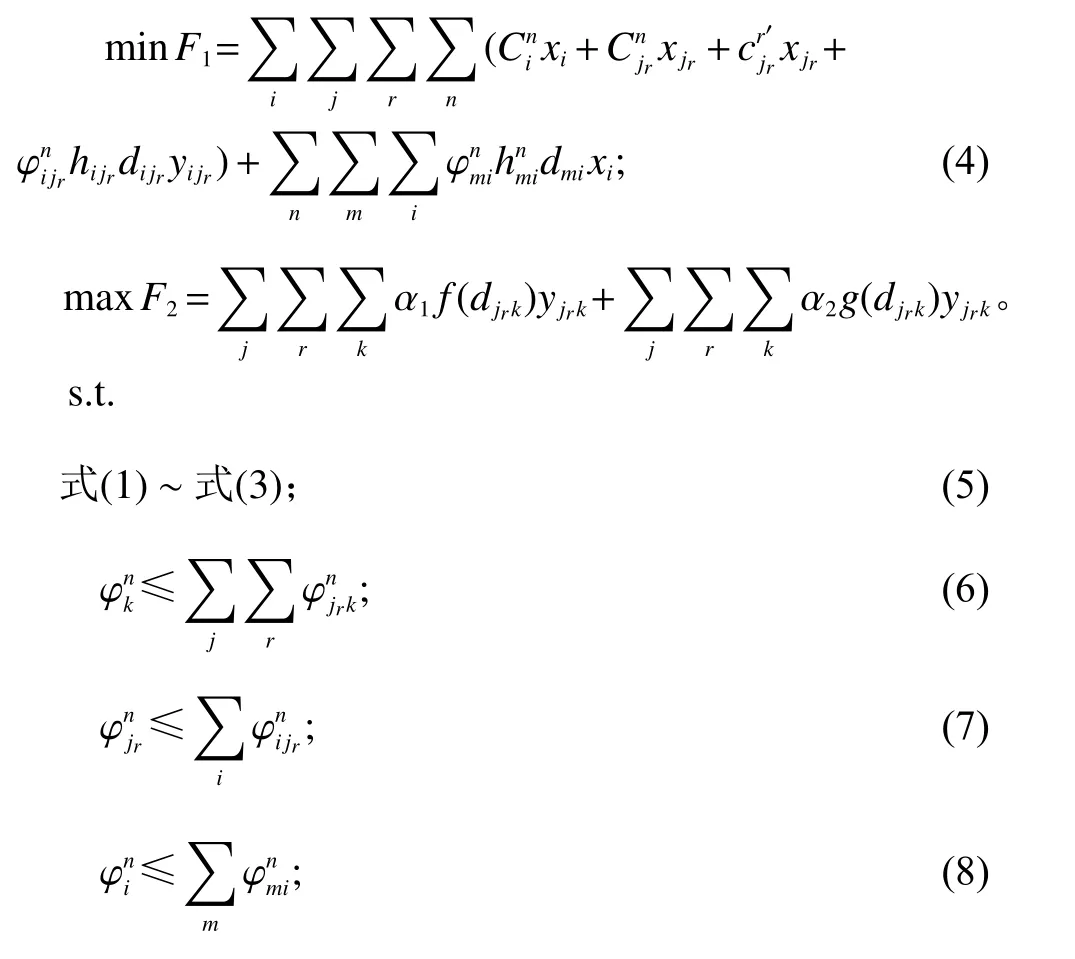
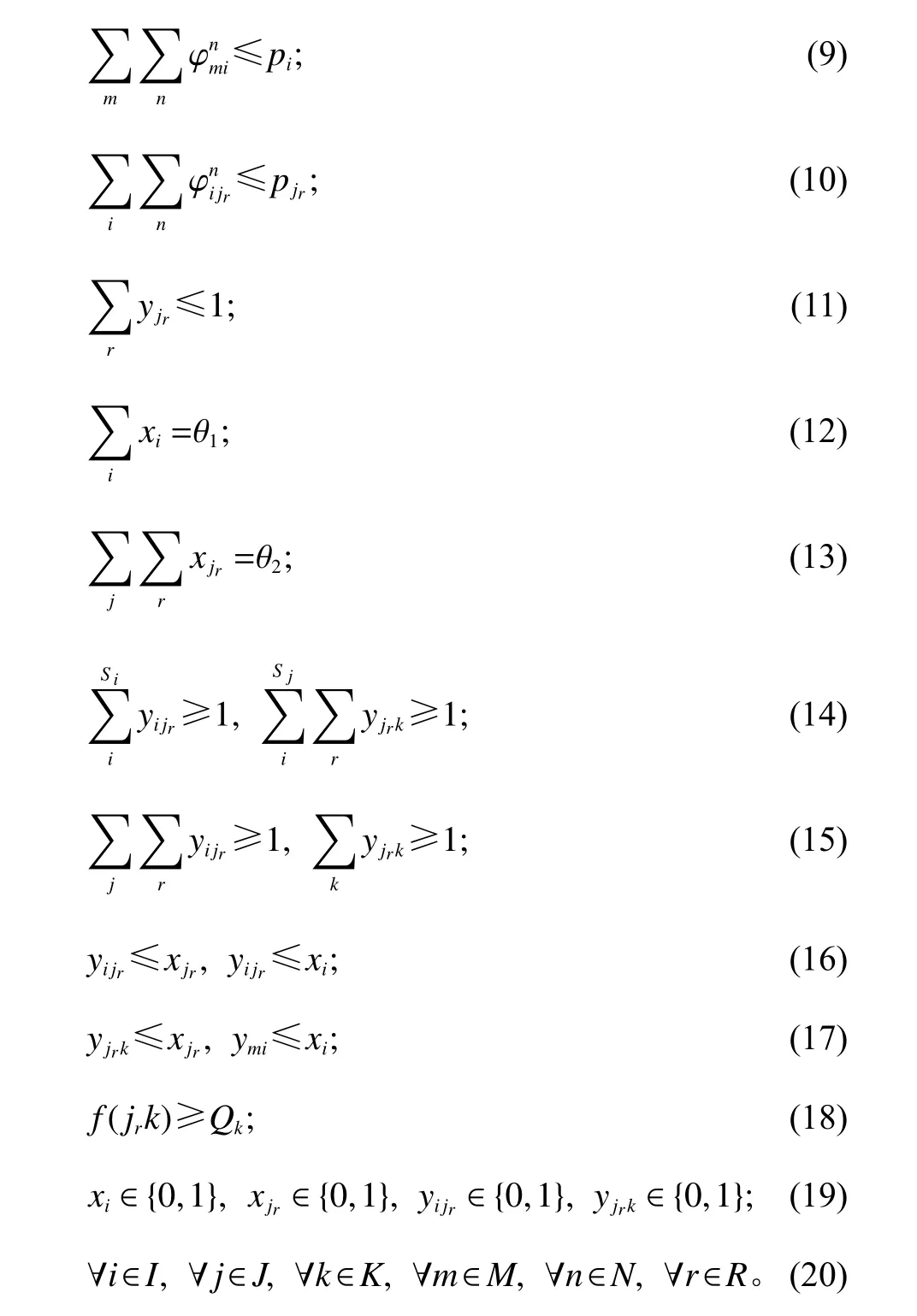
其中，式(4)表示最小化各级网点中各参与企业的建设成本和运输成本；式(5)表示最大化客户对末端网点服务水平的满意度和末端网点服务效率；式(6)～(8)表示各级网点提供给下级网点的快递量应不少于下级网点的需求量；式(9)、式(10)表示各中转站和末端网点接受的量不超过自身容量；式(11)表示每个末端网点或被选为一种服务模式或不被选择；式(12)、式(13)表示被选中的中转站和末端网点应满足数量要求；式(14)表示每个末端网点/客户至少被一个中转站/末端网点服务；式(15)表示每个中转站/末端网点至少向一个末端网点/客户提供服务；式(16)、式(17)表示只有当中转站/末端网点被选中，才可以为下级提供服务，才可以接受上级提供的服务；式(18)表示末端网点提供服务的水平应不低于其服务客户所能接受的最低满意度；式(19)、式(20)为决策变量和参数的取值范围。

本文涉及到多目标优化问题，对于该类问题的求解，一般采用加权法、约束点法、理想点法、目标规划法等。本文采用加权法将多目标函数转化为一个线性目标函数，在统一量纲时，将成本采用离差标准化，满意度和效率函数取平均值，将目标函数(4)与目标函数(5)转化为单目标函数为

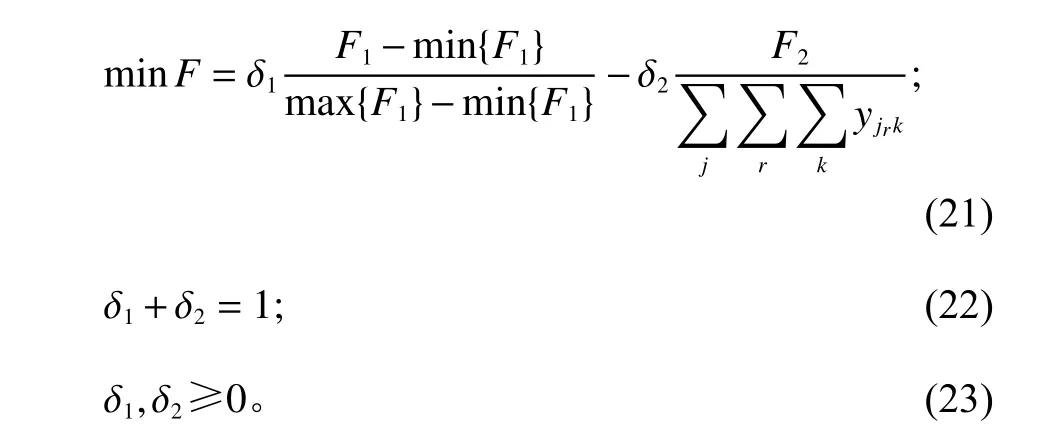
其中，其余约束条件与多目标函数约束条件一致；成本权重系数δ1、顾客满意度与效率函数权重系数δ2，均由决策者偏好决定。

2 算法设计

将多目标优化模型转换为单目标优化模型后，需要解决中转站、末端网点选址定位、末端网点服务模式选择、各级网点服务关系分配等问题，遗传算法针对此类问题已有较为成熟的应用，因此，本文采用遗传算法进行求解。

算法的关键步骤如下。

Step1初始化种群。随机选择若干末端网点和中转站，计算客户点对各末端网点的满意度、距离、对服务模式的偏好及需求量；将客户按照需求量从大到小排序，优先将需求量大的客户分配到服务模式相匹配的最近的末端网点，判断是否超过该点剩余容量，如未超过，该客户分配结束，顺次分配下一个客户，否则，记录该客户点，顺次分配下一个客户；当所有可分配的客户点分配完毕时，将记录的客户点按需求量从大到小排序，将客户顺次分配给服务模式最匹配的末端，计算此方案扩建成本，根据该末端是否服务其他客户点，综合考虑服务模式是否可变更，计算末端模式改建成本，判断扩建、改建的成本大小，选取最终匹配方案；计算各末端网点与中转站的距离、承接的需求量；将各末端网点承接量从大到小排序，优先将量大的末端网点分配到最近的中转站，判断是否超过该中转站剩余容量，如未超过，该末端网点分配结束，顺次分配下一个末端网点，否则，将该末端点分配到次近的中转站，具体分配流程如图2所示。将通过上述步骤生成的末端网点−客户点、中转站−末端网点的对应服务方案作为初始化种群。

Step2计算目标函数适应度。适应度函数是目标函数的直接反映，是利用群体中个体的适应度函数值来指导种群搜索进化的大致方向，本模型中适应度函数为F it(F)=F。

Step3种群进行遗传操作形成子代。首先采用锦标赛选择策略，随后将种群中表示中转站−末端网点的5个方案随机取出2个中转站，将表示末端网点−客户点的20个方案随机取出5个末端网点进行变异，根据图2所示初始化种群步骤再次计算可行解，形成子代。

Step4进行精英保留策略。将父代和经过选择、变异等遗传操作后形成的子代进行合并，产生新一代种群。

Step5判断进化代数。判断算法是否达到最大进化代数，若满足条件则算法终止，不满足则转至Step2，进化代数gen=gen+1。

3 算例分析

3.1 参数设置

按照区域街道用地划分，将居民点聚类成33个需求点，编号1～19的需求点位于住宅区，编号20～25的需求点位于商业区，编号26～29的需求点位于学校区，编号30～33的需求点位于工业产业区。两家参与企业分别简称Y企业和S企业，将在目标区域内布局中转站和末端网点，Y企业共7个备选中转站和20个备选末端网点，S企业共5个备选中转站和18个备选末端网点，需求点、参与企业备选点分布情况如图3所示。

案例数据包括备选中转站坐标、备选末端网点坐标、客户坐标、客户日均需求量、配送单位运输成本、中转站容量及运营成本、不同服务模式末端网点容量及运营成本、允许建设的中转站及末端网点数量、客户感到非常满意时的提货距离和非常不满意时的提货距离、末端网点更换服务模式的改建成本等。参考周林[12]在城市配送选址方面的相关研究，结合调研企业数据，最多允许建立的末端网点数量为25，中转站数量为6，客户群体对末端网点满意度的最小临界距离为400 m，最大临界距离为800 m， δ1、δ2、 α1、α2均取值0.5，其余数据信息如表1～6所示。

图2 考虑末端网点变更的种群初始化流程Figure 2 Population initialization process considering end node change

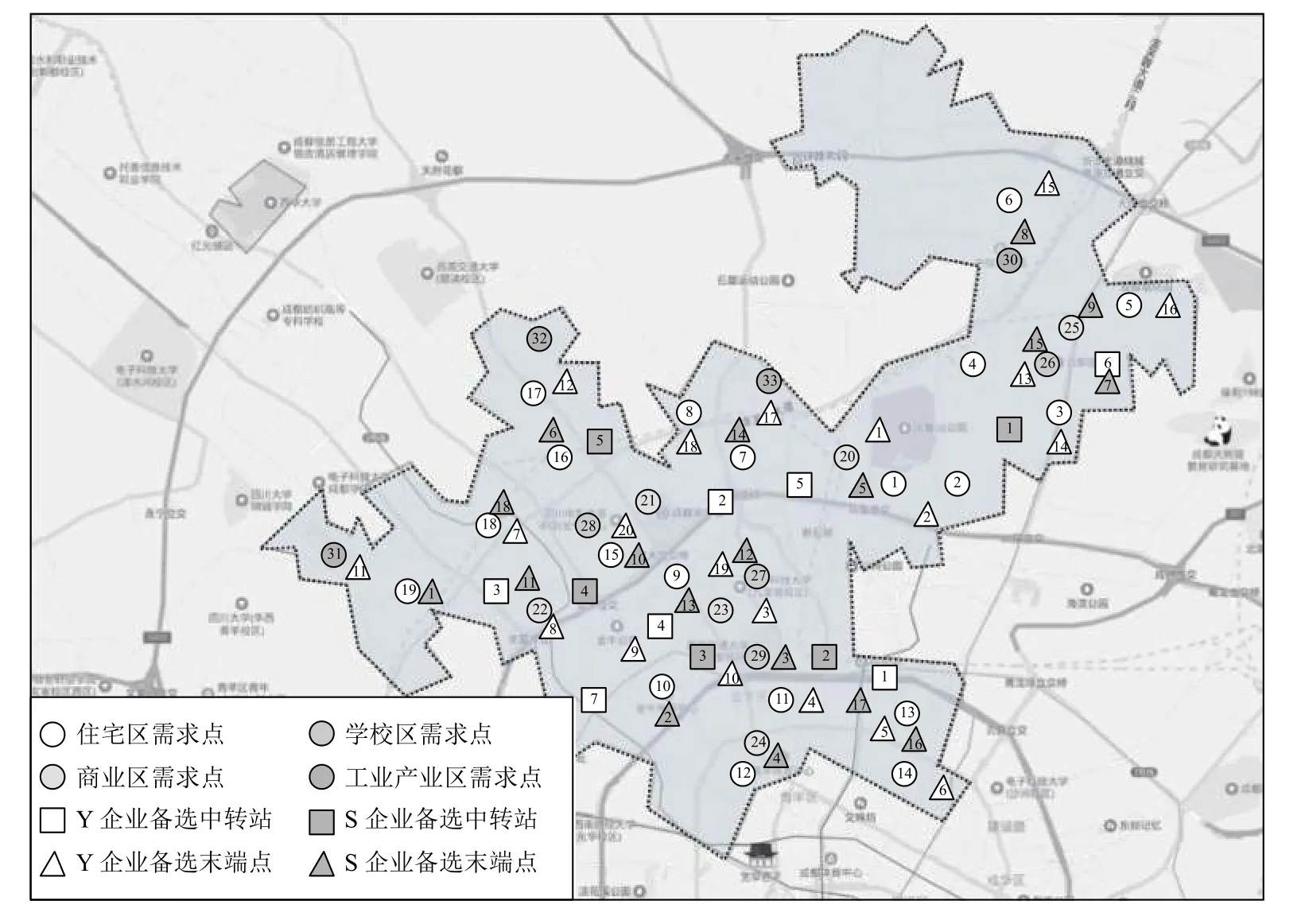
图3 需求点、参与企业备选点分布图Figure 3 Distribution of demand points and alternative points of participating enterprises

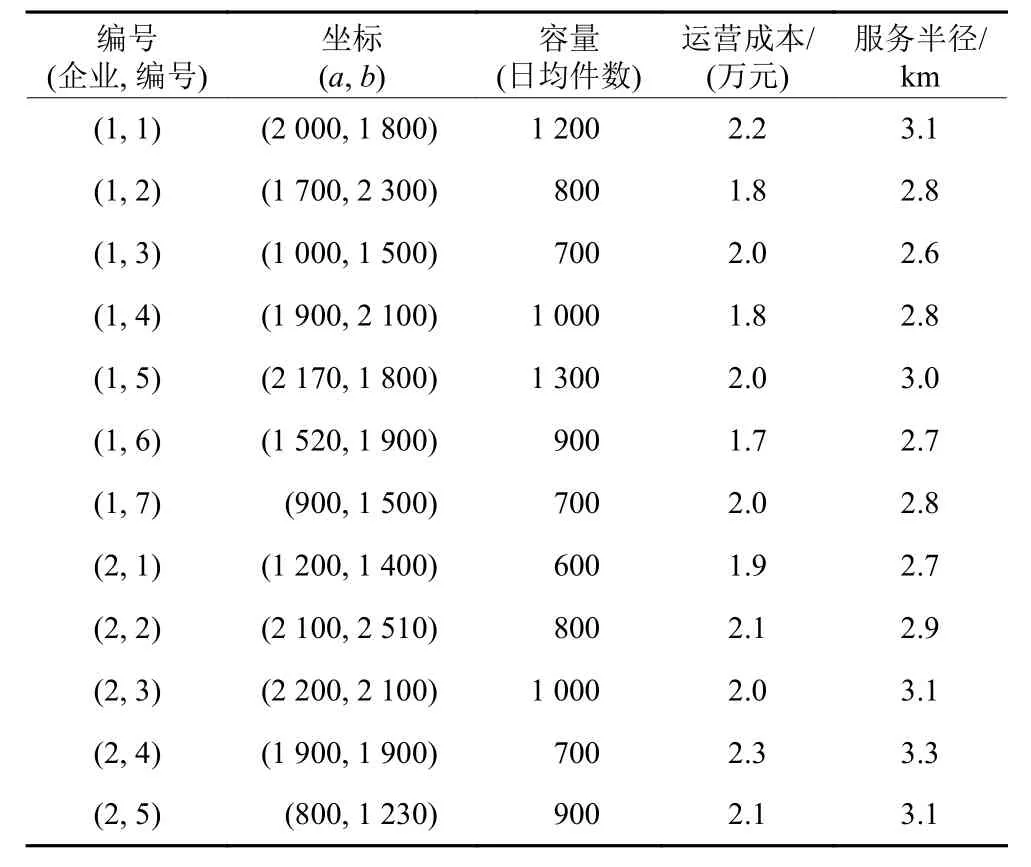
表1 备选中转站坐标、容量及运营成本Table 1 Coordinate, capacity and operation cost of standby selected transfer station

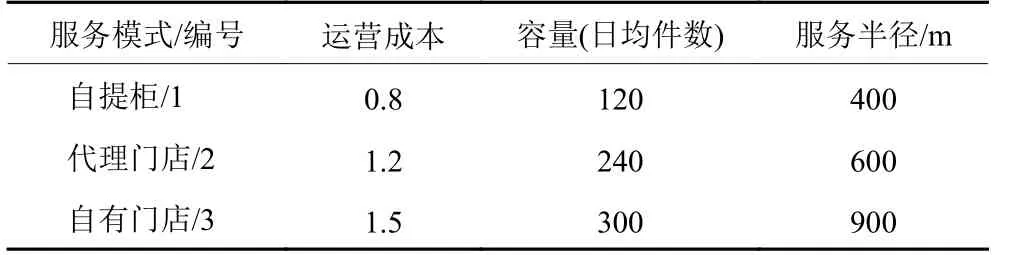
表2 不同服务模式末端网点运营成本、容量及服务半径Table 2 Terminal outlets capacity, service radius and operation cost of different service modes

以表4中第1行数据为例进行说明。若自提柜不变更服务模式，仅进行扩容，扩建成本为每增加20件，成本增加0.1万元；若自提柜变更为代理门店，改建成本为0.2万元；若自提柜变更为自有门店，改建成本为0.4万元；其他模式变更及改建计算成本同理。

3.2 计算结果

本文采用Python进行编程, 对δ1、δ2、α1、α2均取值0.5, 程序结果显示379代以后, 成本、满意度及服务效率综合值保持不变, 可以认为获得最优解。此时系统总成本为411 812.1元, 客户满意度和服务效率的综合值为12.554 82, 系统运输总距离为41 094 m,末端网点的平均服务效率指数为0.08, 平均服务满意度为0.862 5, 对应的最优方案需要建立编号为(1,2)、(1, 5)、(1, 4)、(2, 5)、(1, 6)的5个中转站, 编号为(2, 10)、(1, 15)、(1, 18)、(1, 13)、(1, 6)、(1, 14)、(2, 14)、(2, 5)、(2, 15)、(1, 8)、(2, 9)、(1, 4)、(2, 3)、(2, 2)、(1, 20)、(2, 4)、(2, 13)、(2, 16)、(2, 11)、(1, 19)的20个末端网点, 末端网点发生服务模式变更或扩建的共有6个, 在保证满足所有客户需求的同时达到客户满意度和服务效率最优。中转站−末端网点、末端网点−客户的对应服务关系如表7和表8所示。

表3 备选末端网点坐标、现有服务模式Table 3 Coordinates of alternative end nodes and existing service modes

表4 末端网点变更服务模式及改建成本Table 4 Service mode change and reconstruction cost of terminal outlets 万元

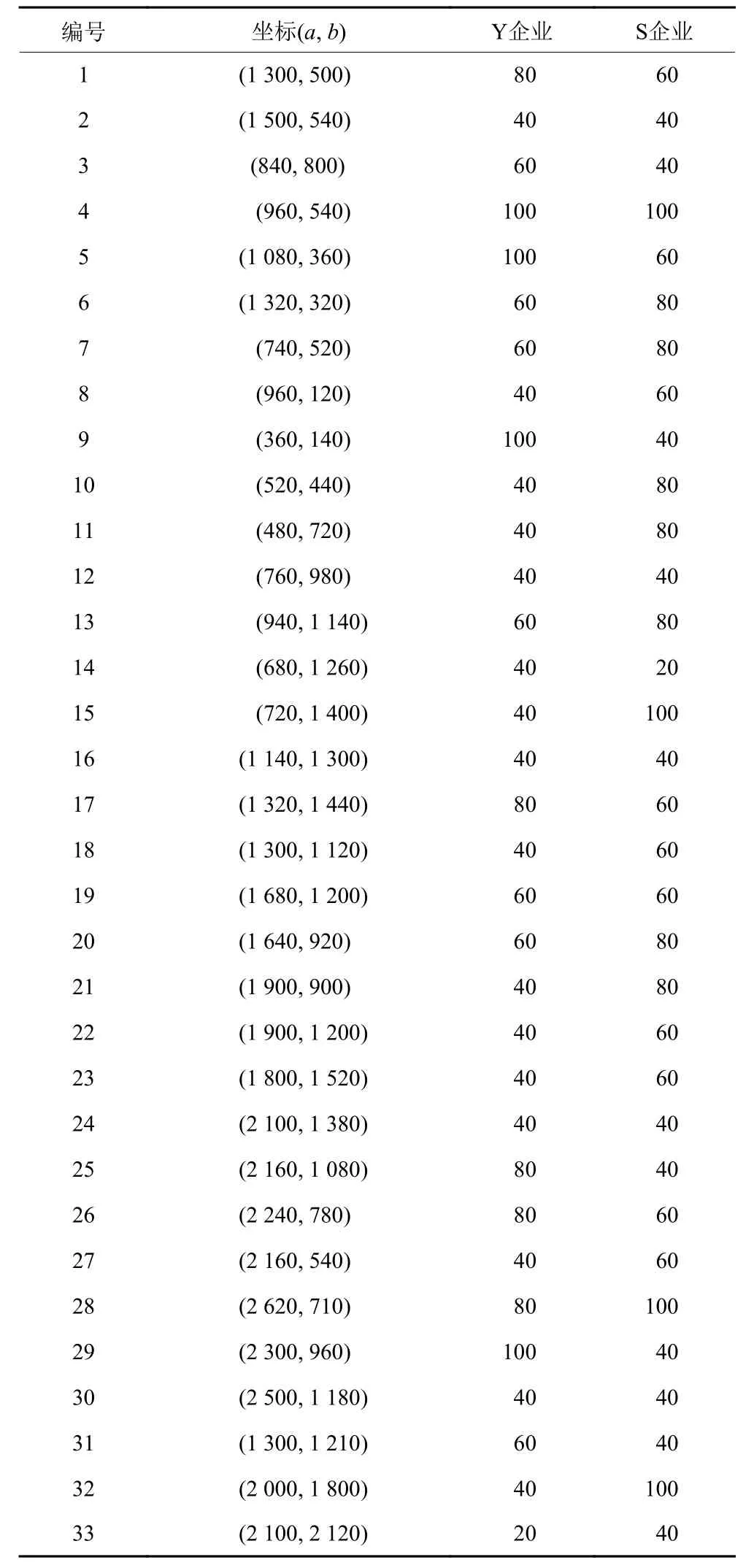
表5 客户点坐标及对参与企业需求量Table 5 Customer point coordinates and demand for participating enterprises 日均件数

表6 客户对末端网点服务模式评价Table 6 Customer's evaluation on the service mode of terminal outlets

不考虑末端网点的改建或扩建，仅考虑网点共享时，求解过程将算法种群初始化步骤简化，随机选取若干末端网点和中转站，依据客户需求量大小顺次分配即可，此时得到系统总成本为423 370.7元，客户满意度和服务效率的综合值为9.924 138，系统运输总距离为47 252 m，对应的最优方案需要建立6个中转站和23个末端网点。如果考虑末端网点的改建和扩建，系统的总成本会降低2.73%，客户满意度和服务效率提高26.51%。2种情况下顾客满意度对比如图4所示。

表7 中转站−末端网点对应服务关系Table 7 Corresponding service relationship between transfer station and terminal outlets

表8 末端网点-客户对应服务关系Table 8 Service relationship of terminal outlets and customers

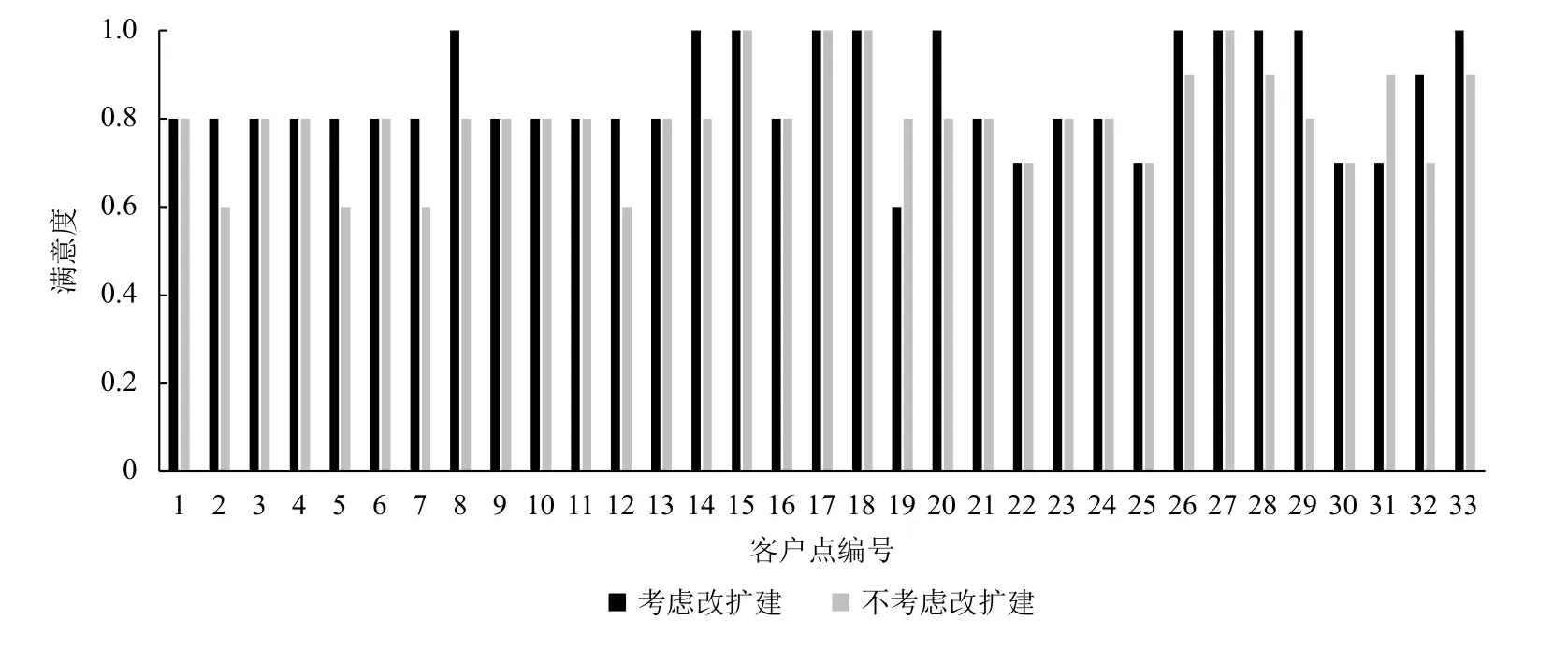
图4 考虑网点共享时2种情况下客户满意度对比Figure 4 Comparison of customer satisfaction in two cases under network sharing

不考虑网点共享，仅考虑末端网点的改扩建时，求解过程与不考虑末端网点改扩建类似，此时得到系统总成本为516 114.1元，客户满意度和服务效率的综合值为11.852 88，系统运输总距离为73 284 m，对应的最优方案需要Y企业和S企业各设置3个中转站，共6个中转站，分别设置14个、12个共26个末端网点。如果考虑网点共享，系统的总成本会降低20.2%，客户满意度和服务效率提高5.92%。

3种方式的结果对比如表9所示。

表9 3种方式计算结果对比Table 9 Comparison of calculation results of three methods

此外，为分析决策者决策偏好对结果的影响，本文在同一实验数据下，选取不同的 δ1、δ2值，比较在不同的决策偏好下，系统总成本与满意度和服务效率综合值的变化情况，结果如图5所示。在同一实验数据下，选取不同的 α1、α2值，比较决策者对客户满意度和网点服务效率在不同的重视程度下，系统总成本的变化情况，结果如图6和图7所示。

从图5中可以看出，决策者对成本和满意度、服务效率的选择偏好对结果有较为明显的影响。增大成本权重时，系统总成本呈下降趋势，但当成本权重超过0.5时，成本可降空间变小。此外，随着成本的降低，客户满意度和服务效率综合值持续下降，且下降趋势没有减缓。从图6和图7中可以看出，决策者对客户满意度和网点服务效率的不同重视程度均会对系统成本造成一定影响。通过对比可以看出，服务效率权重增大比满意度权重增大对系统总成本的影响略小。通过对比图5～7可以看出，仅考虑客户满意度，不考虑服务效率时，系统总成本达到最大；仅考虑服务效率，不考虑客户满意度时，系统总成本达到最小。

图5 随成本权重 δ1的变化曲线Figure 5 Change curve with cost weight δ1

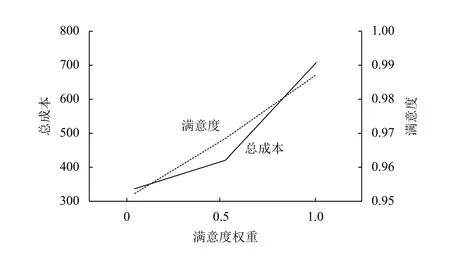
图6 随满意度权重 α1的变化曲线Figure 6 Change curve with satisfaction weight α1

图7 随服务效率权重 α2的变化曲线Figure 7 Change curve with service efficiency weight α2

综上，可以得到如下结论。

1) 仅考虑网点共享，不考虑末端网点的改扩建时，与考虑网点共享及改扩建的选址模型相比，系统总成本略高，客户满意度和服务效率明显偏低。由于顾客满意度受末端网点服务模式影响，若优先考虑满意度，会造成所需末端网点较多；若优先考虑系统成本，即建立尽量少的末端网点，顾客满意度和服务效率会降低。而考虑网点共享及改扩建的选址模型在求解时，针对客户点优先分配服务模式最匹配的末端网点，保证大多数网点的客户满意度及服务效率较优，同时加入改建、扩建求解思路，可以在成本尽量小的情况下将所有客户点分配至满意度较高的网点。

2) 仅考虑末端网点的改扩建，不考虑网点共享时，与考虑网点共享及改扩建的选址模型相比，系统总成本明显偏高，客户满意度和服务效率略低。由于系统成本取决于网点建设、运营成本和运输成本，不考虑网点共享时，为满足所有客户需求，各企业均需建立足够的末端网点和中转站，导致选取的网点不能充分利用其容量，与此同时，运输成本也会随着网点个数的增加而增加。而考虑网点共享及改扩建的选址模型在求解时，首先将各需求点对各企业的需求视为一个整体，在分配时提高网点的利用率，减少所需网点个数，同时也可在一定程度上降低运输成本。

3) 决策者对成本、顾客满意度、服务效率的选择偏好对最终结果有较为明显的影响。相同条件下，增大成本权重可以有效降低系统总成本，但同时也降低了顾客满意度和网点服务效率，当成本权重超过0.5时，顾客满意度和服务效率综合值下降速度将明显高于成本降低速度，当满意度或服务效率的权重超过0.5时，系统总成本的增加速度也会有提升。因此，为了系统整体达到最优，决策者在权衡成本与满意度、服务效率间的关系时，应均衡考虑多项影响因素，不宜将成本权重设定过高，应兼顾考虑客户满意度和网点服务效率等因素。

4 结束语

本文针对集散中心−中转站−末端网点的多级快递配送网络，考虑中转站及末端网点共享、末端网点服务模式及容量变更等实际问题，结合服务模式、距离等因素对顾客满意度和网点服务效率的影响，建立考虑系统总成本最小、顾客满意度和网点服务效率的多目标优化模型，并设计改进遗传算法求解，通过实验验证模型的合理性和算法的有效性。问题的解决有利于指导参与企业在提倡资源共享的大环境下，充分利用已有资源，形成共享的城市快递网络，同时针对不同区域客户对末端网点不同服务模式的偏好，打造客户满意度更高、服务响应更快的行业品牌。

本文对城市多级快递网点选址问题提出合理的模型与有效的算法，在未来研究中可继续深入研究。在模型方面，将各参与企业的成本及利益分配等因素考虑进来，在算法方面，不断改进提升算法效率，更好地求解大规模问题。