基于改进贪婪关联算法的在线零售商优化拆单问题

钟丽文，姜同强,2

(北京工商大学 1.计算机与信息工程学院；2.农产品质量安全追溯技术及应用国家工程实验室，北京 100048)

针对在一个区域拥有多个配送中心的在线零售商，拆单是指一张订单需拆分成多张订单，由同一区域的不同配送中心进行配送。企业实践表明，通过调整各配送中心存储的单品(最小存货单位)，每降低1%的拆单率，原本每年需履约的包裹数量将减少约100万件。因此，若在线零售商具有巨大订单数量，可直接减少企业运输成本，提高顾客服务满意度。拆单率算法本质就是对单品进行分配，所以通过对单品分配方法进行研究以降低拆单率是物流优化的一个重要问题。

目前，学者主要集中于通过研究订单拆分，进行配送路径的规划与优化，库存商品拣选效率的提高以及物流成本的降低等领域。Dullaert等[1]通过订单拆分来满足不同运输方式的选择，提出一种元启发进化算法。秦雨虹等[2]将拆单规则与配送相结合建立联合优化模型。张源凯[3]考虑订单在多个仓库的拆分及匹配问题，设计启发式算法对订单分配模型进行优化，从而降低物流配送成本。韦超豪[4]通过对订单拆分策略研究设计了订单分批算法。王善超[5]依据订单是否可拆分建立相应的订单拣选模型，进而提高仓库商品拣选效率。韩曙光等[6]、章园园[7]以2种拆单方式为原则建立配送路径规划模型，并采用改进的蚁群算法求解最优配送路径。符卓等[8]、夏扬坤等[9]针对需求依据订单拆分的车辆路径问题，设计禁忌搜索算法对建立的车辆路径规划模型进行求解。

较少学者关注通过单品分配方法研究订单拆分以降低拆单率的问题。Xu等[10]提出一种基于订单实时发生的动态优化方法，通过重新分配订单降低拆单率。Catalán等[11]考虑在线零售商一地多仓场景下的单品分配问题，建立最小化订单配送次数模型，设计启发式贪婪算法对模型进行求解，实验表明，启发式贪婪算法可降低约10%的拆单率。李乐乐[12]提出环形算法对单品进行分配，拆单率可降低约8%。李建斌等[13]在多仓单品存储策略一定的基础上，对单仓单品数量不足所引发的拆单进行了研究。

上述研究虽然均降低了拆单率，但环形算法未考虑订单中单品间的关联性；启发式贪婪算法仅使用两个单品在所有订单中共同出现的次数衡量单品间的相关性，衡量标准较为单一，因此上述算法存在改进空间。本文在已有研究的基础上，结合Apriori算法，寻求订单中具有强关联关系的单品，提出一种新的单品分配方法，并对原有算法进行改进，实现了拆单率显著降低的目标。

1 建立模型

1.1 问题描述及基本假设

导致拆单的主要原因包括品类拆单、数量拆单和标记拆单。其中，品类拆单指在一张包含多种单品的订单中，至少有2种单品不在同一配送中心存储；数量拆单指订单包含缺货的单品；标记拆单指订单中包含属性不同的单品，如订单同时包含常温商品和冷藏商品。本文在仅考虑品类拆单的情况下，以拆单率为衡量指标，对现有算法进行改进。模型基本假设如下。

1) 在线零售商的销售环境稳定；

2) 本文仅考虑品类拆单的情况；

3) 同一区域具有多个配送中心(即一地多仓)；

4) 配送中心具有容量限制，一个配送中心无法存储所有单品；

5) 一种单品至少存储于一个配送中心中；

6) 所有的配送中心能满足全部订单。

1.2 建立最大化整单配送模型

本文符号设计及决策变量定义如下。

S为单品的总品类数量，s表示第s种单品；D为配送中心的数量，d表示第d个配送中心；O为订单总数量，o表示第o个订单；Cd为第d个配送中心可容纳单品的最大品类数；Io为第o个订单中包含的单品的集合。

整数规划模型如下。

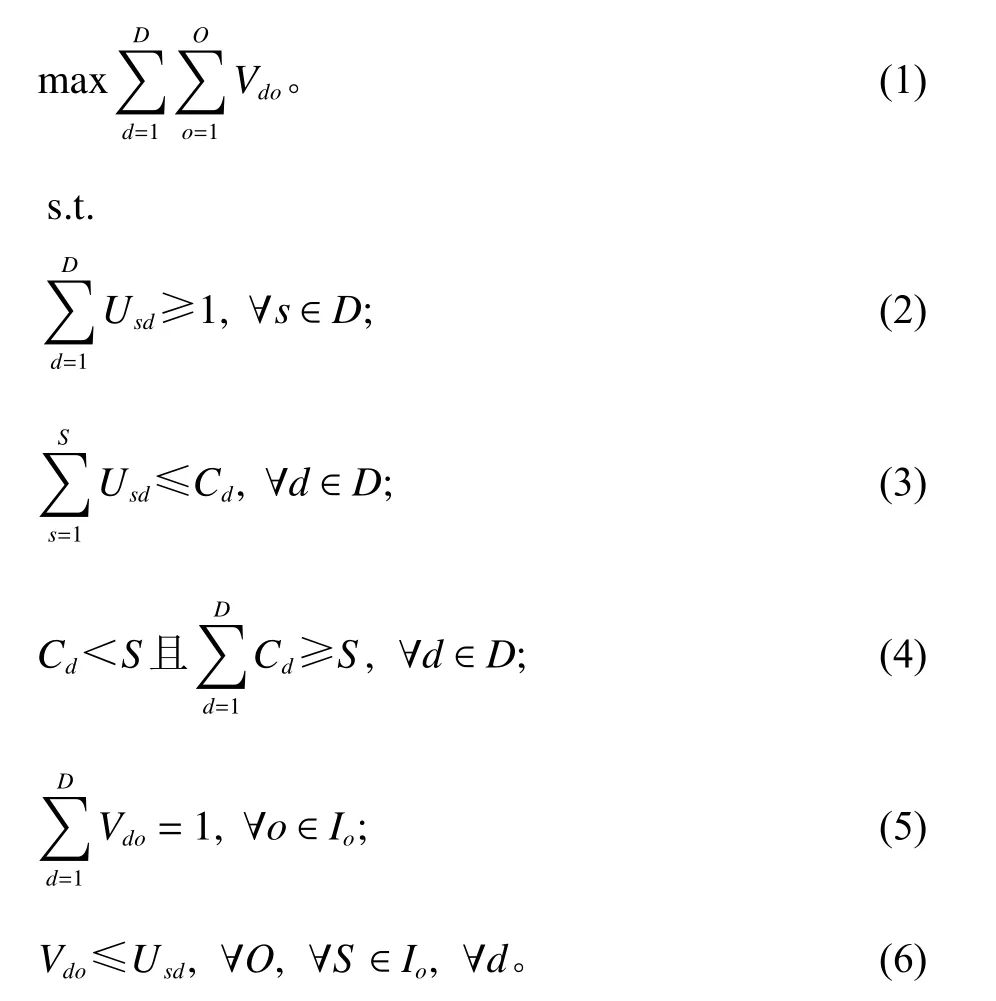
式(1)为目标函数，求解所有配送中心能完成整单配送的最大订单数量；式(2)约束每种单品必须分配给一个配送中心；式(3)约束每个配送中心存储的单品不能超过该配送中心的单品种类容量上限；式(4)约束一个配送中心不能存放所有单品，但全部配送中心可以；式(5)表示订单o由第d个配送中心完成配送；式(6)表示第d个配送中心对订单o进行配送的前提条件是该配送中心存放了订单o所需的单品。

Catalán等[11]学者经过分析，证明在仅考虑品类拆单情况下的订单拆分问题为NP-hard问题，因此难以用精确的算法对该模型进行求解。

2 贪婪关联算法设计

本文旨在研究在线零售商一地多仓场景下的拆单率算法来求解单品分配模型，并通过改进拆单率算法调整单品的分配策略，达到明显降低拆单率的目的。仅考虑品类拆单的情况下，在线零售商一地多仓运作存储如图1、图2所示。

图1 原始单品存储策略Figure 1 Original stock item storage strategy

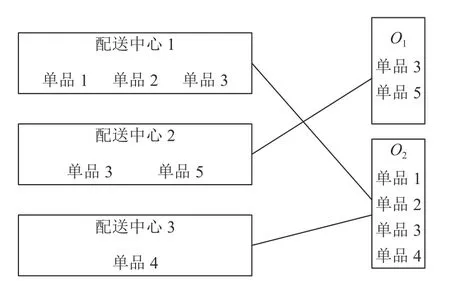
图2 调整后的单品存储策略Figure 2 Adjusted single product storage strategy

由于配送中心容量有限，各配送中心存储的单品和各订单所需单品如图1所示。现订单处理系统需将订单O1、O2分配给相应的配送中心，因单个配送中心不包含O1、O2所需全部单品，故需将O1、O2拆分成多张订单进行4次配送。在其他条件不变的情况下，对各配送中心存储的单品进行调整，调整后的单品存储策略如图2所示，此时经3次配送即可完成2张订单。

综上，仅考虑品类拆单的情况，在多仓运作模式下，配送中心先根据某种分配方法选择存储的单品。当订单下达时，订单管理系统根据各订单对单品的需求，直接或拆分成多张订单分配给配送中心，单个配送中心完成的订单整单配送数量越多，拆单率越低。因此设计较为科学的拆单率算法是降低拆单率的核心。

2.1 现有算法

本文选用贪婪订单算法和贪婪热销算法[11]为对比算法。贪婪算法的核心是求解各子问题的贪婪策略的选择，在贪婪订单算法中，优先选择包含单品数量多的订单进行分配，再根据一轮分配结果选择与已分配单品在订单中共同出现次数最多的未分配单品进行分配。在贪婪热销算法中，优先选择热销单品，使各配送中心均包含热销单品。提高各配送中心对仅包含热销单品的整单履行率，对于未分配的非热销单品，贪婪热销算法同样采用共现矩阵对其进行分配，并保证剩余未分配单品只分配给1个配送中心。其中，销量排名前B类的单品为热销单品，共现矩阵用于描述2个单品在订单中出现的次数，定义热销品类数量B和共现矩阵为

现有算法流程如图3和图4所示。

贪婪订单算法和贪婪热销算法的贪婪策略选择，启发本文对单品分配方法的进一步探讨。不同的单品分配方法对求解算法的质量产生不同的影响。从图3、图4中可以看出，虽然贪婪订单算法和贪婪热销算法在二次分配时均使用共现矩阵来描述已分配单品和未分配单品间的关联性，但其第1次分配时均未考虑订单中单品间的关系，并仅用2个单品在订单中共同出现的次数衡量单品间的相关性，衡量标准较为单一。

2.2 贪婪关联算法

图3 贪婪订单算法Figure 3 The greedy order algorithm

经典的关联算法——Apriori算法，最早应用于分析购物篮中不同商品间存在的关联关系，关联规则挖掘在本文中表述如下。所有项目集合I={单品1,单品2, ···, 单品s}，事务数据集D={O1, O2, ···, OO}，且事务 O ⊆I ，关联规则A→B，其中， A ⊂I ，B ⊂I且A∩B=Ø，A、B为单品的集合，称为项集。支持度Support为D中包含项集A和B的事务数与总事务数的比值；置信度Confident为D中同时包含项集A和B的事务数与只包含项集A的事务数的比值。可分别表示为

图4 贪婪热销算法Figure 4 The greedy sales algorithm

支持度的大小影响最终生成的关联规则的数量和质量。若min_sup水平太低，则产生巨量候选项集，不但降低算法的挖掘效率，并产生很多无意义的关联规则。若min_sup水平太高，则容易遗漏潜在的不易发现的关联规则。置信度的大小影响最终生成的关联规则的相关强度。最小置信度min_conf控制关联规则的可预测能力；合理的min_conf可在期望预测范围内生成关联规则[14]。基于上述分析，本文通过Apriori算法求解订单中单品间的强关联关系，为改进现有拆单率算法提供新的思路，改进的贪婪关联算法的具体步骤如下。

Stage1：

Step1 设置min_sup，min_conf。

Step2 1_项候选项集R1←扫描D。

Step3 1_项频繁项集L1←Support(R1)≥min_sup。

Step4 2_项候选项集R2←L1join L1。

Step5 2_项频繁项集L2←Support(R2)≥min_sup。

......

Step6 k_项 频 繁 项 集Lk←Support(Rk−1)≥min_sup。

Step7 (k+1)_项候选项集Rk+1=Ø←Lkjoin Lk, 进入Step8。

Step8 强关联规则←{[Support_count(Lk)]/ Support_count(s)}≥min_conf，其中，s为Lk的所有非空子集，Support_count(X)=||{ J ∈D | X ⊆J||。

Step9 强关联单品表←遍历所有强关联规则。

Stage2：

Step1 设置配送中心的数量d，配送中心d的容量限制Cd。

Step2 index list ←赋予配送中心唯一索引index。

Step3 单品表←遍历所有订单O中包含的单品。

Step4 Q ←强关联单品表中单品的数量。

Step5 强关联单品表←按Confident大小对强关联规则降序排序。

Step6 对每个配送中心d，如果∃Cd＜Q：

Step6.1 分配强关联单品表中包含的前Cd个单品给Cd＜Q的配送中心d;

Step6.2 将配送中心d从index list中删去。

Step7 如果Cd＞Q：

Step7.1 分配Q个单品给所有配送中心;

Step7.2 计算共现矩阵W=RTR;

Step7.3 对每个未分配的单品:

Step7.3.1.1 计算未分配单品与已分配单品间的平均共现次数;

Step7.3.2 找到平均值最高的配送中心d，将单品分配给该配送中心d;

Step7.4.1 找到最小index的配送中心d;

Step7.4.2 根据共现矩阵W，找到与已分配单品共现次数最多的未分配单品;

Step7.4.3 将单品分配给配送中心d。

3 算法实验

3.1 原始数据预处理

算法测试采用一家在线零售商订单交易数据。其中，OrderNO为订单编码，SKUNO为单品编码，Quantity为每张订单中单品的销售数量，Total为每个单品的销售额。由于原始数据中存在缺失值和异常值的数据记录仅约占所有数据记录的0.08%，因此在实验过程中直接将其删除。为便于算法的实现，对数据进行预处理，预处理结果显示，共有2 750张订单，2 546个单品，一张订单包含的单品种类数量在2～94种之间。

3.2 参数设置

适当的min_sup和min_conf可挖掘出潜在的有趣关联规则并使关联规则具有更好的预测能力[14]。因此为确定适当的min_sup和min_conf，实验在min_sup分别为0.1%、0.25%、0.5%、0.75%、1%，min_conf分别为70%、80%、90%的水平下，观察候选项集、频繁项集和强关联规则的数量变化及算法运行效率。选择候选项集、频繁项集和强关联规则的适中数量及运行效率的min_sup和min_conf为贪婪关联算法的实验参数。因为每张订单包含的单品数量在(2,94)之间，范围过广，所以Apriori算法的测试结果以生成3项频繁项集为例进行分析。实验结果如图5～7所示。

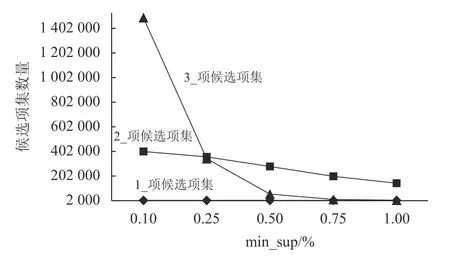
图5 不同min_sup水平下候选项集数量对比Figure 5 Comparison of the number of candidate sets underdifferent min_sup levels

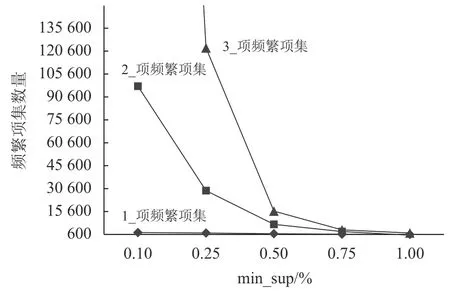
图6 不同min_sup水平下频繁项集数量对比Figure 6 Comparison of the number of frequent item sets under different min_sup levels

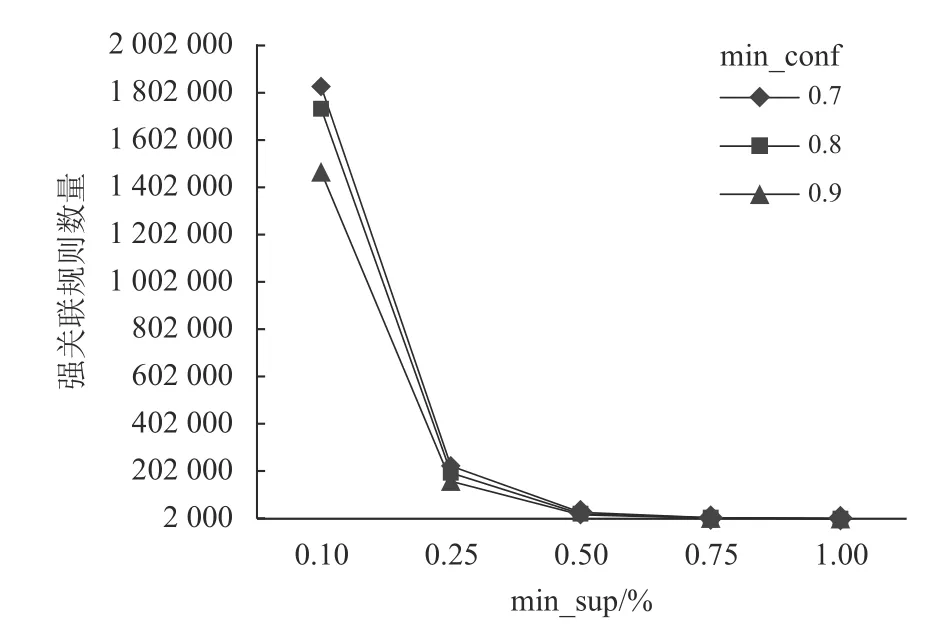
图7 不同min_conf和min_sup水平下强关联规则数量对比Figure 7 Comparison of the number of strong association rules under different min_conf and min_sup levels

从图5～7中可以看出，在不同min_sup水平下，随min_sup的增长，2_项、3_项的候选项集和频繁项集数量不断减少。在同一min_conf水平下，强关联规则数量具有相同变化规律。具体当min_sup为0.1%和0.25%时，算法产生巨量2_项、3_项的候选项集、频繁项集及强关联规则；当min_sup为0.75%和1.0%时，各项集和强关联规则数量骤减；当min_sup为0.5%时，候选项集、频繁项集和强关联规则的数量均处于测试结果的中间水平。在同一min_sup水平下，随min_conf水平的上升，强关联规则数量下降，但min_conf过高则容易遗漏潜在的关联规则。算法在不同min_sup和min_conf下的运行时间如图8所示。

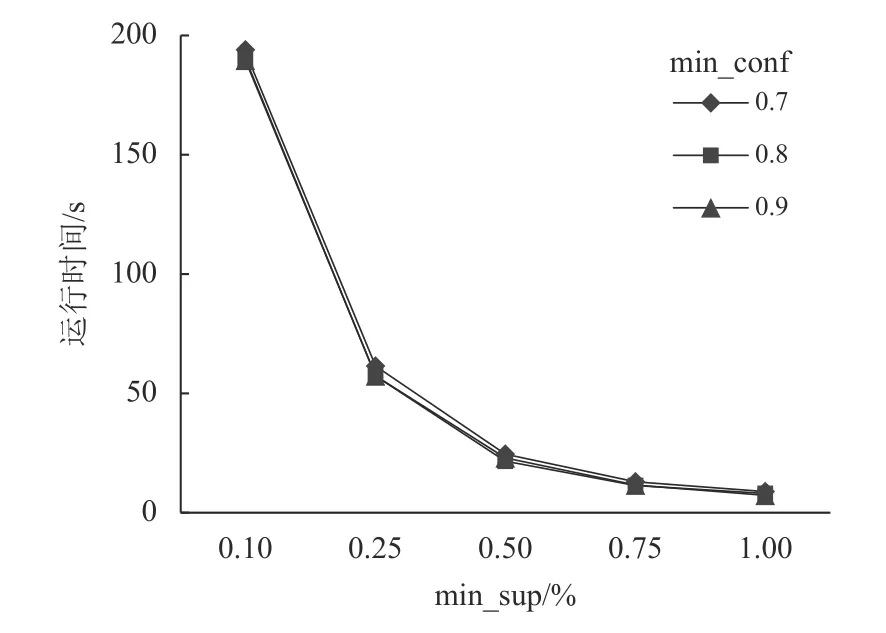
图8 不同min_sup和min_conf水平下算法运行效率对比Figure 8 Comparison of algorithm operation efficiency under different min_sup and min_conf levels

图8 表明，在同一min_conf水平不同min_sup水平下，min_sup水平越高，算法运行所需时间越少，而在同一min_sup水平不同min_conf水平下，算法运行耗费的时间没有较大的变化。

综合Apriori算法各参数的测试结果，在贪婪关联算法的第1阶段，选取min_sup=0.5%，min_conf=70%进行实验。本文假设在一个区域内有3个配送中心，每个配送中心的容量相同，并且单个配送中心的单品种类容量上限Cd=0.7 S，算法采用Python3.0编码实现。

3.3 实验结果分析

定义拆单率为需要拆分的订单在总订单中所占比例，则贪婪关联算法、贪婪热销算法和贪婪订单算法的表现结果如表1所示。

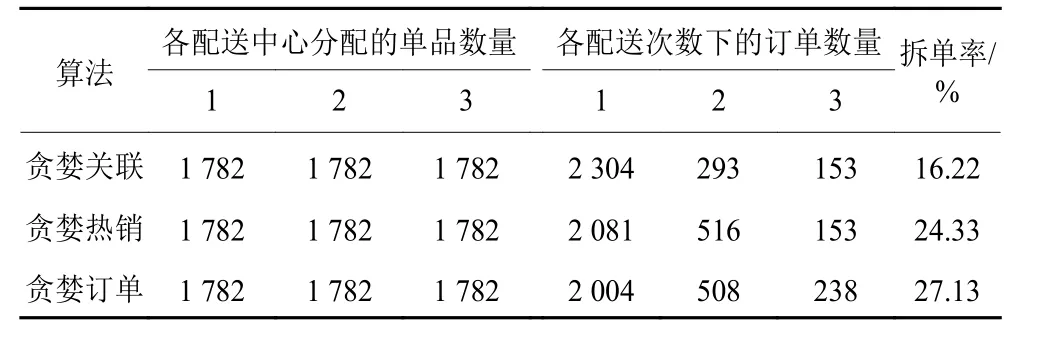
表1 各算法拆单率比较Table 1 Comparison of the split order rate of each algorithm

表1记录不同算法下，分配给各配送中心的单品数量、各配送次数下的订单数量及拆单率情况。实验结果显示，相比贪婪热销算法和贪婪订单算法，贪婪关联算法拆单率分别下降8.11%和10.9%。虽然各算法拆单率数值都比较大，但对订单数据进行观察发现，原始订单数据中包含10种单品以上的订单数量约占总订单数量的70%，而在文献[11]中，平均每个订单包含的单品种类数量为5.17[11]，文献[12]采用的订单生成算法设定每张订单包含的单品种类数量在2～10种之间[12]。因此算法可能因数据集的不同而呈现不同的拆单率表现，单张订单包含单品数量越多，发生拆单的概率越大。但实验结果表明，和其他算法相比，贪婪关联算法是有效的。

4 结语

本文从仓储管理的角度，建立最大化订单整单配送模型。对于在线零售商一地多仓运作的情况，对贪婪订单算法和贪婪热销算法的单品分配方法进行研究。针对上述算法存在的不足，结合Apriori算法，提出一种改进的拆单率算法。通过对各配送中心存储的单品进行调整，从而使拆单率显著降低，进而减少在线零售商的运输成本及其总体运营成本。最终实验结果表明，贪婪关联算法的表现优于贪婪热销算法和贪婪订单算法。

在线零售商实际运营过程中，配送中心的单品存储策略需参考多个因素，因此本文可在以下方面进行拓展研究。例如，除了考虑品类拆单外，未来可以结合数量拆单和标记拆单进行分析；为提高算法效率，未来可以采用深度学习算法对数据进行挖掘。