概率积分法参数反演的SAAFC模型

叶 伟 徐良骥 张 坤1

（1.安徽理工大学空间信息与测绘工程学院，安徽 淮南 232000；2.深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232000）

我国存在大量的建筑物、水体和铁路的“三下”压煤［1-2］，“三下”采煤造成的建筑物裂缝、倾斜甚至坍塌、铁路塌陷、水体流失等现象普遍存在，对人民生命财产安全以及生态环境产生了较大影响。因此对煤炭开采引起的地表移动变形进行精确预计显得尤为重要。煤炭开采地表移动变形预计的常用方法有全曲线拟合法、特征值法、剖面函数法和概率积分法［3］，其中概率积分法仍然是目前开采沉陷预计的主要方法［4-6］。概率积分法因其所用的移动和变形预计公式中含有概率积分而得名，基础理论是随机介质理论，又可称为随机介质理论法［7］。提高概率积分法参数的反演精度是运用概率积分法进行地表移动变形预计的关键。现有的最小二乘法［8］、模矢法［9］等传统算法适合进行非线性程度较低的模型参数反演［3］；神经网络算法、遗传算法、粒子群算法、模拟退火算法等智能优化算法在过去数十年内进行参数反演时取得了较好效果［10-14］，但这些基于生物进化理论的智能优化算法反演的参数存在随机性［3］。为了提高概率积分法参数的反演精度，有必要引入新的反演方法［15］。

目前关于概率积分法参数反演的流行方法是群智能寻优算法，如人工蜂群算法［16］、果蝇算法［17］、蚁群算法［18］等。人工鱼群（Artificial Fish Colony，AFC）算法是中国学者李晓磊等于2002年提出的一种模拟鱼类群体行为方式的新型群智能寻优算法［19］。AFC算法求解最优化问题可理解为生成的初始鱼群内的各条人工鱼分别模拟鱼的4种行为（觅食、聚群、追尾、随机），并比较各行为经过试探后视野内的食物浓度，再用公告牌记录食物浓度最高的点和当前食物浓度值并选择食物浓度最高的一种行为继续执行［20-22］。通过这种寻优方式，可以实现目标问题的最优化求解［19-21］。该算法具有全局寻优、计算迅速、初始值要求低、参数设定容许范围大的特点［20］。但是由于AFC算法的视野和步长都是给定的固定值，往往制约了鱼的活动范围和行动能力，使得算法存在求解精度偏低、收敛速率慢的局限性［20］。针对AFC算法的收敛速率和求解精度不高的问题，诸多学者提出了不同的改进方法，如通过多条人工鱼动态影响某条鱼的步长、利用迭代次数动态影响视野和步长的鱼群算法、采用混合寻优鱼群算法等来提高算法的求解精度和收敛速率［20-22］。本研究以朱集东矿1242（1）工作面为例，采用刘彦君等［23］提出的一种变步长和变视野的改进人工鱼群算法，即自适应人工鱼群（Self-adaptive Artificial Fish Colony，SAAFC）算法，并结合矿区开采沉陷预计理论，对概率积分法参数进行精确反演。

1 工程实例概况

朱集东矿1242（1）工作面位于-906 m水平西一盘区，开采11-2煤层。该工作面于2013年7月开始回采，到2015年4月地表稳定。工作面倾斜长220 m，实际回采走向长1 292 m，平均采深949 m，煤层平均采厚为1.8 m，煤层倾角3°，可近似视为水平煤层。本研究在1242（1）工作面上方地表沿煤层走向和倾向方向上分别设置了一条走向观测线和一条倾向观测线，走向观测线设置了83个监测点，并以“ML”作为点名进行编号，倾向观测线设置了61个监测点，并以“MS”作为点名进行编号，倾向和走向观测线共设置了11个控制点。走向观测线整体近似平行于工作面走向方向，倾向观测线则与煤层走向方向成锐角分布，该角度为77°11'。1242（1）工作面形状及其岩移观测站布设如图1所示。

2 模型建立与参数反演

2.1 SAAFC算法

针对AFC算法的局限性，本研究采用SAAFC算法［23］来反演概率积分法参数。SAAFC算法的步长和视野改进思路为：迭代前，计算出的某条人工鱼与公告牌（记录最优行为）中当前状态最优人工鱼的距离VisualF，将其作为当前人工鱼的视野，再引入视步系数a（0～1区内的随机数），令步长为视野的a倍，最后将步长和视野代入到人工鱼的4种行为中进行计算［21-23］。在SAAFC算法中，将每条人工鱼的步长和视野更改为动态变化并确保随着迭代次数增加，步长和视野逐渐变短［21-22］。假设某一人工鱼用F表示，最优人工鱼用Fbest表示，则自适应算法中人工鱼的视野和步长可分别表示为［22］

式中，VisualF表示人工鱼F的视野；StepF表示人工鱼的步长［22］。

人工鱼的觅食行为、聚群行为、追尾行为、随机行为可分别按照下列方法执行：

（1）觅食行为。设当前人工鱼的状态为Xi，在其感知范围内随机选择一个状态Xj，按照式（3）执行［21，23］。

式中，a为视步系数［22］。

定义f(Xi)为当前状态人工鱼适应度函数，Yi为相应函数值；f(Xj)为异于当前状态人工鱼的适应度函数，Yj为相应函数值。若Yj=f(Xj)>Yi=f(Xi)，则

否则重新选择Xj，判断是否满足前进条件，尝试Try_Num次后，若仍不满足，则按规则随机前进一步：

式中，Xj为异于当前状态的人工鱼；为尝试Try_Num次选择后的当前状态人工鱼；为按规则随机前进一步得到的当前状态人工鱼。

（2）聚群行为。设当前状态人工鱼为Xi，探索当前邻域内的伙伴数目nf及中心位置Xc。若Yc/nf>δYi′，表明伙伴中心有较多食物且不太拥挤，则朝伙伴的中心位置方向前进一步，按照式（6）执行［21，23］。否则，执行按式（3）规则的觅食行为。

（3）追尾行为。设当前状态人工鱼为Xi，探索当前邻域内所有伙伴中Xj的Yj最大，则朝Xj的方向前进一步，按照式（4）执行［21，23］。

（4）随机行为。若人工鱼在觅食试探次数达到最大后适应度仍无明显改善，则执行随机行为，在定义域内随机选择一种状态人工鱼，然后向该方向移动，按照式（5）执行［21，23］。

2.2 参数反演的SAAFC模型

2.2.1 概率积分法预计原理

利用概率积分法进行地表移动变形预计时主要涉及8个参数，分别是下沉系数q，主要影响角正切tanβ，开采影响传播角θ0，水平移动系数b，下山、上山开采边界拐点偏移距S1、S2和走向左、走向右开采边界拐点偏移距S3、S4。其中，拐点偏移距会受到老采空区影响，当工作面靠近老采空区时，拐点偏移距会向老采空区方向偏移，否则，向本工作面内侧平移［24-25］。因此在进行概率积分法预计时必然要考虑拐点偏移距的存在，考虑拐点偏移距的工作面称为计算工作面，计算工作面和实际工作面在几何上存在一定差异，具体关系如图2所示［7］。

工作面计算尺寸和实际尺寸之间的关系可表示为［7］：

式中，α表示煤层倾角，（°）；D1和D3表示工作面实际开采宽度和长度，m；L和l分别表示工作面计算宽度和长度，m。

利用概率积分法进行地表移动变形预计时，地表任意点A(x,y)的下沉和沿任意方向的水平移动预计模型如图3所示［7］。

概率积分法地表变形移动预计公式分别为［7］：

式中，Wmax为充分采动条件下地表最大下沉值，mm；Wmax=mqcosα，其中，m为平均采厚，mm；erf()·为概率积分法中涉及的误差函数；r为主要影响半径，m；，其中，为平均采深，m；x为地面任意点A点的横坐标，m；y为地面任意点A点的纵坐标，m；φ为计算水平移动时任意方向与X轴正向的夹角，（°）；分别是A点位于X轴上任意位置时，有限开采条件下A点下沉和水平移动量，mm；分别是A点位于Y轴上任意位置时，有限开采条件下A点下沉和水平移动量，mm；

将式（11）、式（12）代入式（10）得到：

2.2.2 SAAFC模型构建与参数反演

模型在参数反演中涉及的单条人工鱼是指8个概率积分法参数中在定义域内的某一参数值；最优人工鱼是指使得目标函数最小的当前生成的8个参数空间的某8个概率积分法参数；鱼群规模是指初始状态时由定义的参数解空间生成的8个参数的总数量；视野是在得到当前最优解状态后继续进行寻优过程中，参数总量中存在的概率积分法参数与最优参数之间的差距；步长是在视野基础上乘以视步系数达到变步长的目的，以实现随着迭代次数的增加逐渐逼近最优解。觅食、聚群、追尾、随机4种行为表示所建模型对8个概率积分法参数的4种寻优方式。

模型选取包括下沉系数q、主要影响角正切tanβ、水平移动系数b、开采影响传播角θ0和拐点偏移距S1、S2、S3、S4在内的8个参数作为最优解输出。PIP=[q,tanβ,b,θ0,S1,S2,S3,S4]为目标参数空间；Scale为其解空间。概率积分法参数反演问题因此转换成在给定解空间中搜索能满足目标函数值最小的一组全局最优解向量［26］。目标函数为

式中，ERROR为目标函数；Wi为实测下沉量，mm；Wi′为预计下沉量，mm；UEWj为实测走向水平移动量，mm；UEWj′为预计走向水平移动量，mm；USNk为实测倾向水平移动量，mm；USNk′为预计倾向水平移动量，mm；m、n、o分别为参与模型反演的下沉点和走向、倾向水平移动点数量。

本研究参考朱集东矿与1242（1）工作面邻近的工作面岩移观测站实测数据解算的概率积分法参数，并根据1242（1）工作面的地质采矿条件查阅参考文献［2］，设定解空间为Scale=[0.51.0；1.5 1.9；0.3 0.6；88 90；22 32；66 76；80 90；135 145]。

基于SAAFC算法的概率积分法参数反演步骤为［22］：

（1）给定基本参数，如鱼群规模FN，单条人工鱼尝试的最大迭代次数、视步系数、初始步长、初始感知距离等参数。

（2）初始化包括当前的迭代次数fn为1，在定义域内随机生成FN条人工鱼。

（3）计算鱼群个体间各条人工鱼的适应度值，用公告牌记录当前最优的人工鱼的状态。

（4）计算每条人工鱼与最优人工鱼的距离并作为当前状态下该条人工鱼的视野，并计算步长。

（5）每条人工鱼模拟觅食、聚群、追尾、随机行为，选择行动后适应度值最优的行为执行。

（6）人工鱼模拟一次行为后均要检验自身适应度值及最优的人工鱼的适应度值，并更新公告牌。

（7）终止条件，fn是否达到最大迭代次数；否则，执行fn=fn+1，转步骤（4）。

本研究采用MATLAB语言实现基于SAAFC模型的概率积分法参数反演，流程如图4所示（图中“N+”表示正整数）。

根据1242（1）工作面概况和建立的SAAFC概率积分法参数反演模型，选取了走向和倾向观测线共73个监测点的实测数据参与模型反演，其中走向42个监测点，倾向31个监测点。经过反复测试分析得到最优解状态下的参数设置为初始鱼群人工鱼数量为200，最大迭代次数为1 500，最大试探次数为450。SAAFC模型反演所得的概率积分法参数如表1所示。

3 结果与讨论

3.1 模型精度评定

结合保存完好的点位的高程观测数据并考虑到平面观测数据的完整性，选取部分监测点的实测数据用于检验模型反演精度。SAAFC模型反演精度主要通过决定系数［27］和泛化性能指标［28］进行综合评定。

跟据监测点下沉拟合值和拟合误差值计算决定系数，公式［27］为：

式中，SSR为预计下沉值平方和［27］；SSE为预计误差平方和［27］。将相关数值代入式（15），计算得RW2=0.930 0，拟合度较好。

采用威尔莫特一致性指数（IWA，Willmott's Index of Agreement）来评定模型的泛化性能，一般认为泛化性能大于0.6时，所求参数具有预计价值［20，28］。

式中，wi为实测下沉值，mm；i为预计下沉值，mm；为实测下沉值平均数，mm，。

将相关数据代入式（16）得到模型泛化性能值为0.971 7，说明模型反演所得参数具有较高的沉陷预计可靠性。

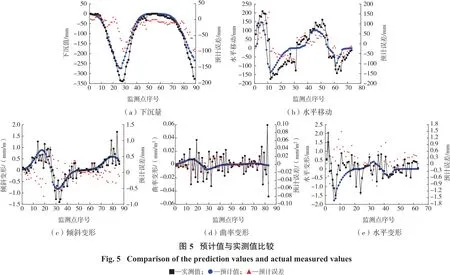
基于SAAFC模型反演的参数（表1）以及概率积分法原理，预计了1242（1）工作面岩移观测站各监测点的下沉量、水平移动、倾斜变形、曲率变形及水平变形，与相应的实测值的误差分布如图5所示。

根据图5（a）可知：下沉预计效果较好，误差分布曲线显示的最大下沉点附近误差值较大，主要是因为能够为解空间提供参考的相邻工作面岩移参数量较少，导致解空间参数范围设置方面存在偏差；其次是所建模型为了降低复杂度和提高收敛速率并未将工作面地质采矿条件引入模型。其他监测点的下沉预计误差为0～20 mm，说明整体预计效果较好。根据图5（b）可知：极少部分监测点水平移动实测值与预计值相差超过100 mm，其他监测点水平移动实测值与预计值误差均保持在50 mm以内，超过100 mm的异常点处于高大树干下方，信号遮挡严重是主要误差来源，总体可看出水平移动预计效果较好。根据图5（c）、5（d）、5（e）可知：倾斜变形、曲率变形及水平变形等3种变形在不考虑极少部分异常点的情况下，整体误差保持在较低水平，预计效果较好。

3.2 模型反演参数精确性和收敛速率评定

岩移观测站设计包括若干条走向观测线和若干条倾向观测线，因此通过实测数据难以绘制出真实下沉曲面，故将倾向观测线和走向观测线各监测点下沉量拟合成空间下沉曲线，构造成空间实测下沉曲面的主轮廓，并与概率积分法预计的下沉曲面进行比较。根据表1得到1242（1）工作面拟合下沉盆地与实测空间下沉曲线如图6所示。根据图6（a）中实测空间下沉曲线形状可看出1242（1）工作面开采倾向并未达到充分采动，走向近似达到充分采动，因此实际下沉曲面应呈现出以走向为长轴的近似椭圆开口的漏斗形状。图6（b）中拟合下沉曲面从开口形状和漏斗形状整体来看较为接近于上述分析所得的实际下沉曲面，说明拟合效果较好。

在工作面地质采矿条件和参数解空间相同的条件下，分别利用最小二乘法（Least Square Method，LSM）、AFC、SAAFC算法反演的概率积分法参数进行下沉预计和水平移动预计，所得下沉预计中误差和水平移动预计中误差如表2所示。3种模型的参数反演收敛速率如图7所示。

由表2可知：3种算法中，SAAFC算法在下沉预计，走向、倾向方向的水平移动预计中精度都是最高的，未改进的AFC算法的参数反演精度略高于LSM算法。

3种模型在设定迭代次数相同、参数解空间相同、反演参数个数和实测数据相同的条件下反演8个概率积分法参数时，SAAFC算法在迭代1 100次左右达到全局最优解，未改进的AFC算法和LSM算法则需要迭代到1 400次左右才能达到最优解状态，因此SAAFC算法的参数反演收敛速率较高，AFC算法收敛速率略高于LSM算法（图7）。

利用3种模型反演所得概率积分法参数进行了1242（1）工作面走向和倾向监测点的下沉和水平移动预计，将预计结果绘制成空间下沉和水平移动曲线，并与实测下沉和水平移动空间拟合曲线进行对比，如图8所示。

由图8可知：SAAFC算法反演所得参数的预计结果更接近实测下沉空间曲线，其中倾向下沉预计效果优于走向下沉（图8（a））；从水平移动空间曲线（图8（b））来看，走向和倾向的拟合度均较好，按拟合度高低依次为SAAFC、AFC、LSM算法。

4 结 论

（1）结合SAAFC算法的技术优势构建了概率积分法参数反演模型，该模型有助于克服概率积分法参数反演容易陷入局部最优解的问题而达到全局最优解；在建模时对概率积分法参数反演问题进行了简化处理，在参数解空间内随机搜索参数值用于下沉和水平移动预计，并与实测数据进行比较，要求所有误差平方和最小，从而将参数反演问题转化为目标优化问题，在构建适应度函数时同时考虑到下沉元素和水平移动元素，使得约束条件更全面、更符合实际需要。

（2）决定系数、泛化性能指标计算结果以及5种变形预计曲线对比分析表明，SAAFC算法的参数反演性能具有较高可靠性，通过SAAFC算法反演的参数预计的下沉曲面较符合实际情况。相对于AFC算法和LSM算法，SAAFC算法反演参数的收敛速率更高，开采沉陷预计精度更高。

（3）在解空间各参数范围控制方面，未能充分利用朱集东矿1242（1）工作面地质采矿条件建立与概率积分法参数之间的精确量化关系，对模型参数反演精度产生了一定的影响。后续工作中将通过精确控制初始解空间各参数的范围，修正概率积分法固有误差来进一步提升概率积分法参数反演精度。