魔芋精粉机人字齿传动系统动力学性能分析

胡清明 候俊鹏 徐长顺 孙丹丹 杨 铭 白 松 郭建华

(1. 齐齐哈尔大学机电工程学院，黑龙江 齐齐哈尔 161006；2. 黑龙江省智能制造装备产业化协同创新中心，黑龙江 齐齐哈尔 161006)

魔芋中含有44%～64%的葡甘露聚糖，魔芋粉是人体吸收甘露聚糖最便捷途径之一，而其加工工艺直接影响魔芋粉质量。目前魔芋粉加工主要分干法和湿法两种，而魔芋精粉机作为干法加工的关键设备，其传动系统优化对魔芋粉生产效率提升具有重要作用[1-3]。

精粉机传动系统分为4级，前3级分别采用V带、同步楔形带、V带传动，第4级采用同步带传动。传统直齿同步带受齿廓特点影响，带齿啮入轮齿时易产生应力集中，导致带齿受挤压严重影响同步带寿命。而新齿廓人字齿同步带具有自导向带轮无需加挡边、传动精度高、噪声低等优点，可用于实现精准传动[4]。

带传动系统中，同步带与带轮隶属刚柔耦合接触多体动力学范畴，传动依靠带与带轮啮合实现[5]，其啮合传动的复杂性源于传动系统中同步带非线性形变(如带齿变形、多边形效应、节距差等)与啮合状态的多样性[6]。Uchida等[7]利用有限元方法研究了同步带带齿齿形与节距差对载荷分布的影响规律。Koyama等[8]基于弹簧、质量、阻尼系统进行了同步带载荷分布研究。李占国等[9]通过刚柔耦合模型系统分析了3M圆弧齿同步带在不同转速和张紧力下的应力变化。Milanovic等[10]分析了同步带在变转矩条件下的带齿载荷应力分布规律。吴贻珍[11]探究了在不同材料下的同步带的相对疲劳寿命。郭建华等[12-13]研究了准静态工况下新齿廓人字齿同步带结构参数对带齿应力分布影响，并基于空间微分几何与齿轮啮合原理，探究了新齿廓人字齿同步带中不同干涉量对啮合干涉形貌的影响以及螺旋角与干涉量之间的关系。文章拟以魔芋精粉机第4级同步带传动系统为对象，研究其在外部负载不变的条件下，齿线形状对传动系统动力学性能影响，并探究螺旋角、齿间错位系数结构参数对传动系统动力学性能及振动影响规律，旨在为魔芋精粉机传动系统的动力学分析与结构优化提供依据。

1 新齿廓人字齿传动特点

新齿廓人字齿同步带的法面齿廓为基准齿廓，带齿与带轮齿形为共轭齿廓。同步带带齿法面齿廓如图1(a)所示，由半径为r1、r2、r3、r4、r5的5段圆弧曲线连接而成，其齿侧圆弧曲线r4的圆心位于节线。主要参数中，齿高3.5 mm(同节距最高齿高)，侧隙0.1 mm，纵横比0.675，轮槽深3.35 mm。齿廓采用圆弧共轭曲线，其啮合性能优秀、承载能力强，啮合时具有良好自锁性与抗爬齿性。新齿廓人字齿同步带齿形顶部有半径为r1的凹槽，啮合传动过程中可排出齿腔中受挤压空气，有效降低噪声。

图1(b)为轮齿法面齿廓示意图，由半径为ρ1、ρ2、ρ3的圆弧曲线组成，其齿侧圆弧曲线ρ2的圆心在节圆上。

2 齿线形状对传动系统动力学性能的影响

2.1 模型建立与边界条件设定

建立同步带传动系统多体动力学模型，带轮齿数22，有效节径d=66.702 mm，同步带齿数52，节线长L=495.3 mm，带宽B=16 mm。人字齿同步带螺旋角β=30°，齿间错位系数k=0.00。同步带模型如图2所示。

同步带由带背层、强力层、尼龙包布层、带齿组成[14]。材料属性参数如表1所示，仿真时定义同步带沿轴向方向位移为零，带轮与柔性体同步带之间接触方式为GEO contact。初始张紧力400 N，从动带轮施加4 500 N·mm转矩负载，主动带轮施加STEP函数使其以1 000 r/min逆时针转动。同步带网格划分采用solid4单元，单元数量67 801，刚柔耦合动力学模型如图3所示。

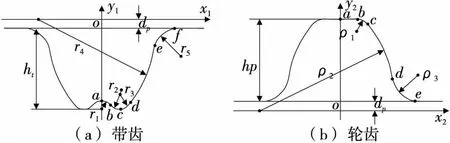
图1 法面齿廓示意图

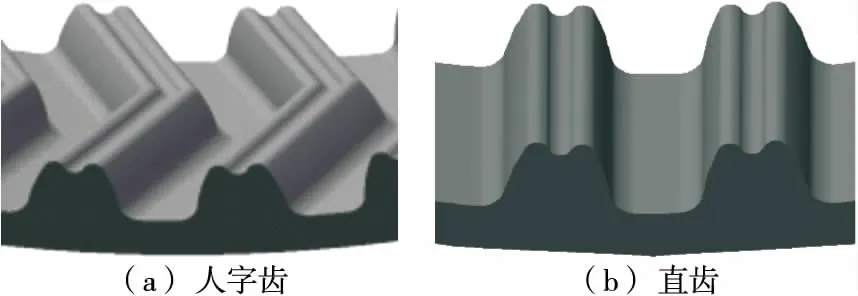
图2 模型示意图

带齿与轮齿啮合传动过程中，带齿啮入带轮齿槽时，由于同步带的柔性体特性，带齿受挤压使得啮合时产生弯曲应力易导致应力集中，应力沿齿向方向非均匀分布，最大应力发生于齿根部位。设定啮合方向如图4所示，选取带齿齿根沿啮合方向前端点N、沿啮合方向后端点M及带齿槽点Q为分析节点。直齿同步带选取同一节点位置，设置仿真时间0.5 s，步数S=500进行动力学仿真。

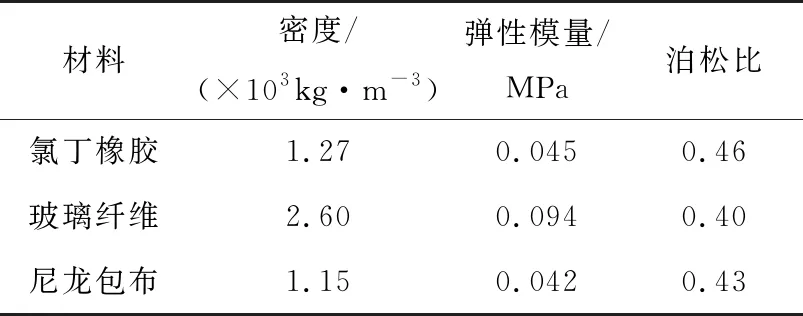
表1 同步带各层材料性能

1. 主动轮转动副 2. 从动轮转动副 3. 从动轮负载 4. 从动轮平动副 5. 刚柔耦合接触副

图4 节点位置

2.2 带齿应力影响

外部负载不变条件下，直齿同步带与人字齿同步带啮合区应力云图如图5所示，带齿根处易产生应力集中，直齿同步带齿根节点最大应力为97.45 N/mm2，人字齿同步带齿根节点最大应力为76.75 N/mm2。

图6为齿根节点M、N在不同齿线形状下应力与时间的波动关系曲线，人字齿同步带啮合区的应力值始终小于直齿同步带的，且直齿同步带在0.00～0.20 s系统加载过程中沿啮合方向前段应力波动较大，波动峰值达86.75 N/mm2。人字齿同步带应力波动更小，传动过程中承载能力更强，工作寿命更长。

2.3 传动系统动力学性能影响

2.3.1 横向振动 同步带传动是摩擦与啮合的复合传动[15]。传动过程中，同步带会产生横向振动。如振幅和振动频率过高，同步带会产生跳齿、爬齿甚至脱齿现象，影响传动精度。在同步带张紧力F=400 N下，通过带齿槽节点Q的XY平面位移幅值进行同步带横向振动分析。图7为新型人字齿同步带传动系统运动轨迹，AB段与CD段为带轮与同步带完全啮合区域，横向振动不明显；BC段与DA段为同步带的松边和紧边，跨距长，横向振动明显。松边的拉应力小于紧边的，振幅更大。

图8为直齿同步带与人字齿同步带松边振幅与时间的波动关系曲线，直齿同步带松边最大振动量为1.925 mm，人字齿同步带松边最大振动量为1.527 mm，因此，人字齿同步带振幅较直齿同步带更小。

图5 应力云图

2.3.2 传动误差 横向振动作用下，同步带产生非线性伸长波动，从动轮角速度在此影响下产生非线性波动导致传动误差。图9为直齿同步带与人字齿同步带从动轮角速度与时间的波动关系曲线，传动系统运转过程中始终保持循环啮合传动状态，故截取一段时间进行分析。由图9可知，运载过程(0.00～0.20 s)中，直齿同步带的导向性低于人字齿同步带的，故其从动轮角速度波动更剧烈、峰值更高，0.20 s后人字齿同步带从动轮角速度波动小于直齿同步带，故传动误差更小。基于文献[16]，人字齿同步带相较于直齿同步带噪声最大降噪11 dB，且横向振动响应更小。综上，人字齿同步带应力分布更均匀，传动误差更小，高速运转更平稳。

图6 应力与时间的变化曲线

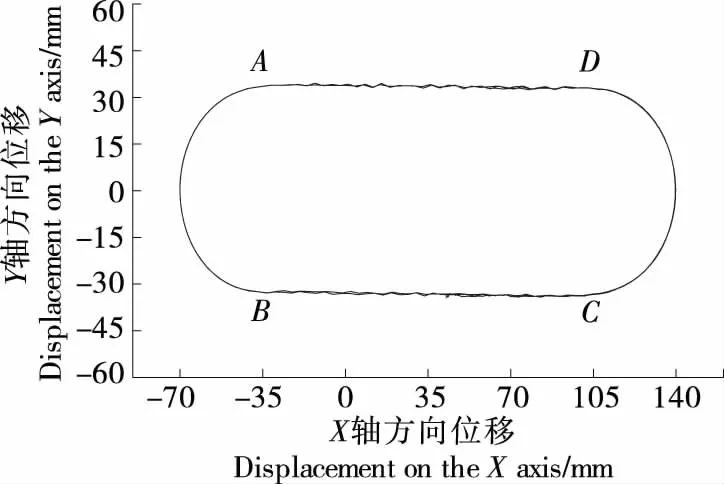
图7 运动轨迹

图8 横向振动

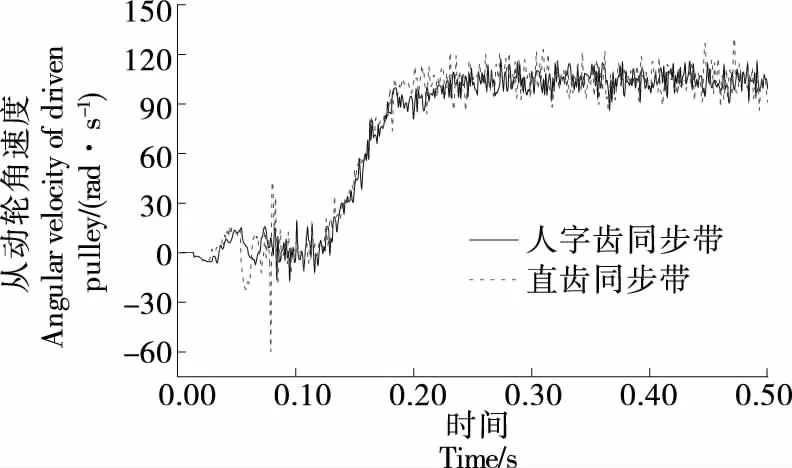
图9 从动轮角速度

3 新齿廓人字齿同步带结构参数优化

3.1 螺旋角对动力学性能的影响

3.1.1 带齿应力 外部负载不变条件下，不同螺旋角同步带同一位置应力云图如图10所示。由图10可知：当螺旋角β=25°时，齿根节点最大应力为93.44 N/mm2；当螺旋角β=30°时，齿根节点最大应力为83.75 N/mm2；当螺旋角β=35°时，齿根节点最大应力为90.72 N/mm2。

图11为同步带齿根节点M、N于不同螺旋角下应力与时间的波动曲线。由图11可知，传动过程中，螺旋角增大，两节点位置应力变化不同。在松、紧边，前端齿根应力随螺旋角的增大而减小；后端齿根应力随螺旋角的增大先减小后增大，且当螺旋角β=30°时，齿根应力达最小值。主、从动轮啮合区，前端齿根应力随螺旋角的增大先增大后减小，幅值小；后端齿根应力随螺旋角的增大而增大，当螺旋角β=30°时，应力值趋于稳定。

由图11还可知，同步带强力层应力始终随螺旋角的增大而增大[17]，螺旋角自β=30°继续增大，强力层应力增大幅值远大于前端齿根(见表2)。故螺旋角β=30°，带齿受力更合理。

3.1.2 横向振动 图12为同步带张紧力F=400 N下，新齿廓人字齿同步带不同螺旋角松、紧边横向振动幅值。由图12可知，螺旋角β=30°时，同步带横向振动幅值最小，紧边最大振动量为0.86 mm，松边最大振动量为1.09 mm。螺旋角越小，同步带导向性越强，因此横向振动越小，但螺旋角越小导致沿啮合方向齿线顶部应力变大，故螺旋角β=30°时新齿廓人字齿同步带传动更为平稳。

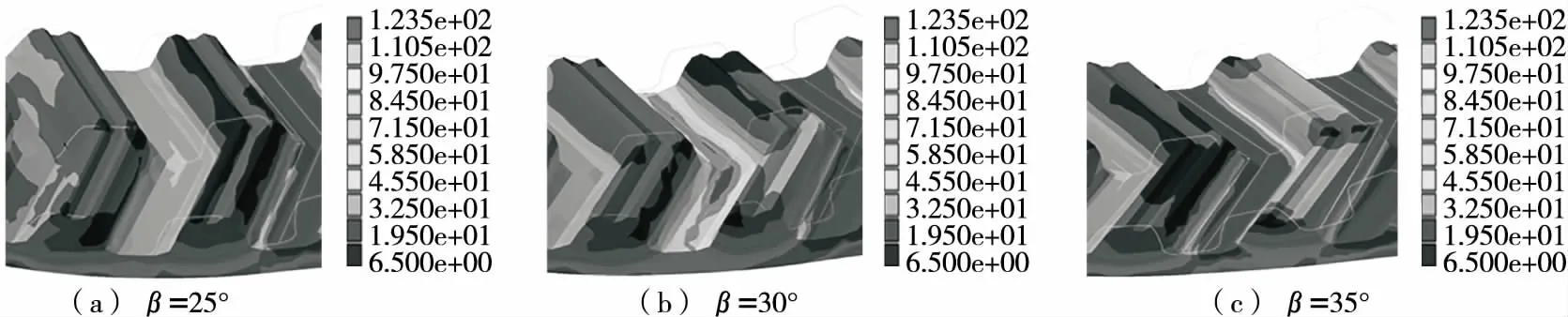
图10 局部应力云图

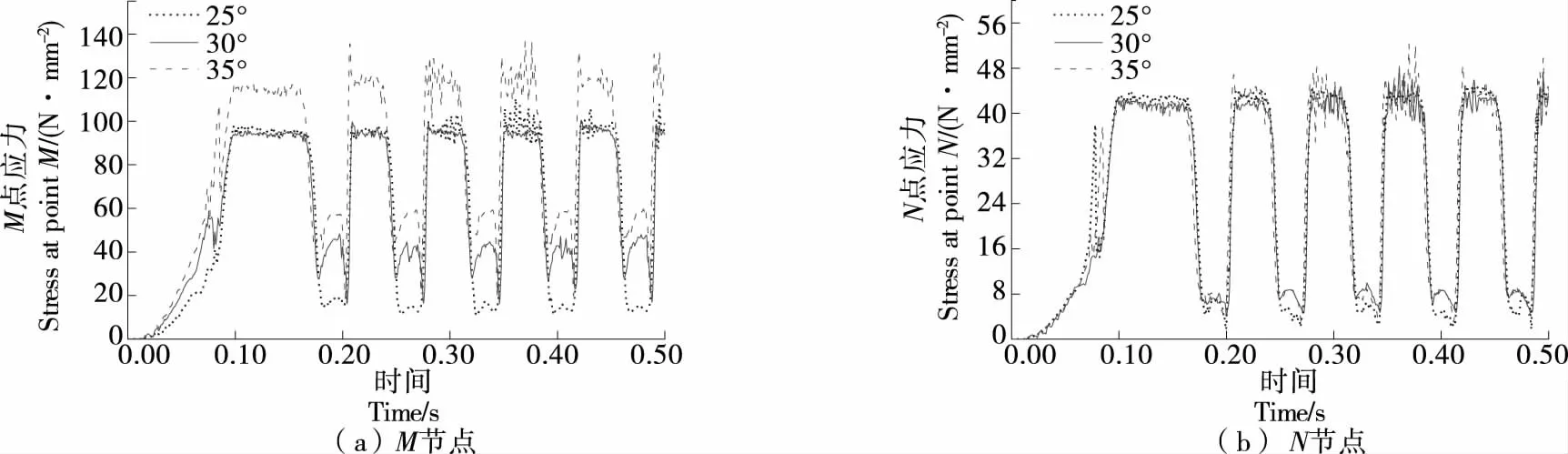
图11 应力与时间的变化曲线

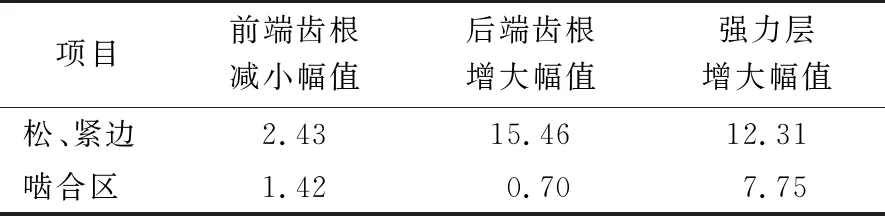
表2 应力变化幅值(螺旋角自30°增大后)

3.1.3 传动误差 带横向振动规律及同步带伸长量波动与从动轮角速度波动呈正相关，即波动幅值越大，传动误差越大。图13为不同螺旋角从动轮角速度波动曲线，系统在0.20 s后进入正常运转状态。由图13可知，螺旋角β=30°时，同步带传动系统角速度波动最小，传动误差最小，即螺旋角越小，同步带啮合传动时的导向性越好，可有效降低带纵向振动及打滑率，提高同步带啮合性能，降低传动误差。

图12 松、紧边位移幅值

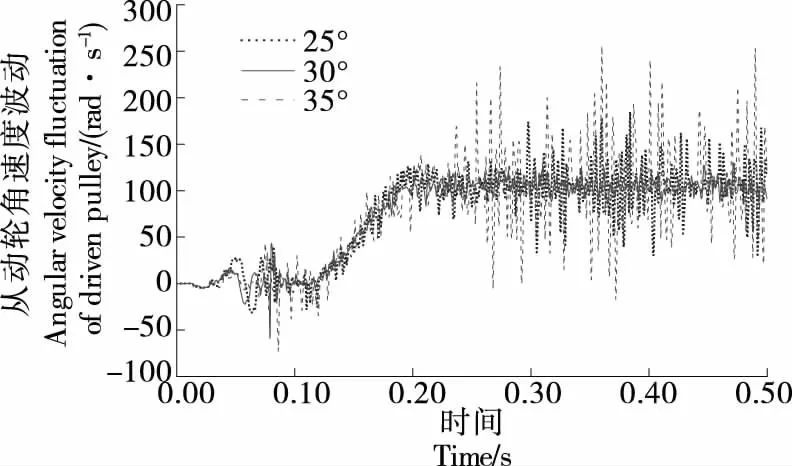
图13 从动轮角速度波动

3.1.4 干涉量波动 动力学仿真过程中，模型接触时会在应力集中区域产生部分边界干涉，干涉深度与应力值呈正相关。若超出干涉深度初始设定值，应力云图中不体现其应力值。由图14可知，0.20 s传动系统进入正常运转状态，螺旋角β=30°时，同步带与带轮干涉深度更小、干涉速度波动量峰值更小且变化更稳定，即应力表现更好，传动更平稳。

3.2 齿间错位系数对动力学性能的影响

3.2.1 带齿应力 外部负载不变条件下，不同齿间错位系数同步带同一位置应力云图如图15所示。由图15可知，当齿间错位系数k=0.00时，齿根节点最大应力为83.75 N/mm2；当齿间错位系数k=0.35时，齿根节点最大应力为84.78 N/mm2；当齿间错位系数k=0.50时，齿根节点最大应力为89.62 N/mm2。

图16为同步带齿根节点M、N于不同齿间错位系数下应力与时间的波动曲线。由图16可知，传动过程中，随着齿间错位系数的增大，带齿齿根应力变化不同。松、紧边，前端齿根应力随错位系数增大而增大且幅值呈递增趋势；后端齿根应力变化与前端齿根相同；主、从动轮啮合区，前端齿根应力随错位系数增大先减小后增大；后端齿根应力随错位系数增大而增大且幅值呈递增趋势。

图14 干涉深度与干涉速度波动

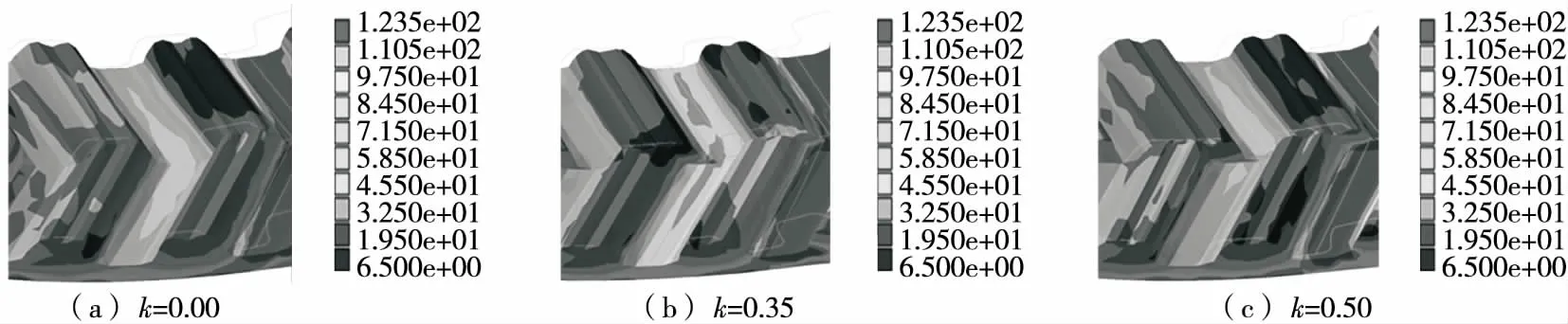
图15 局部应力云图

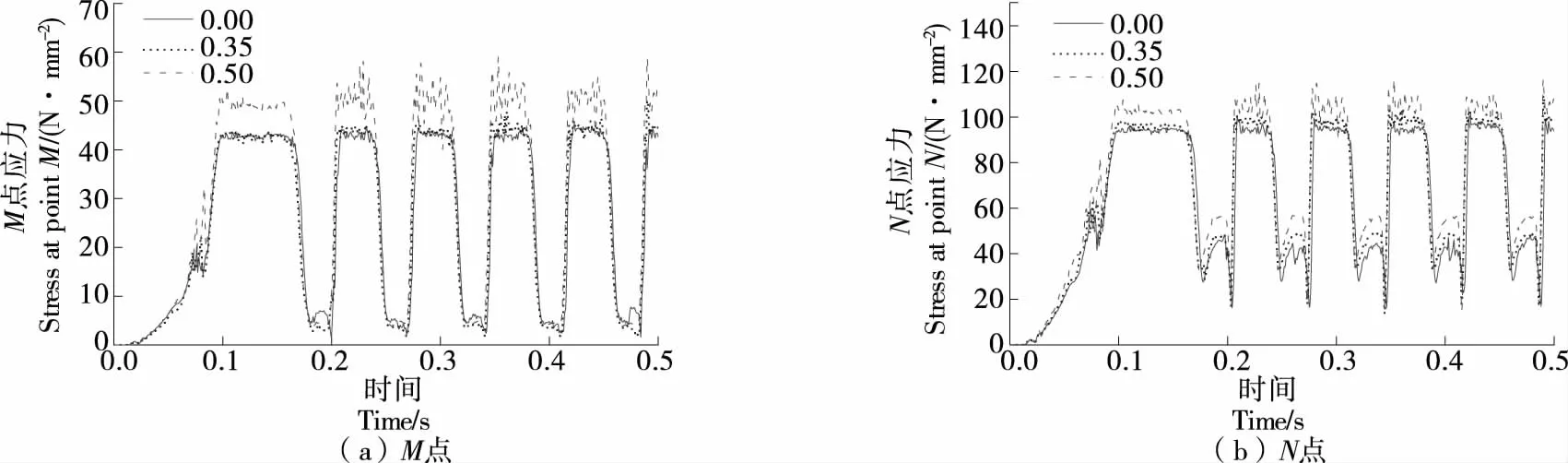
图16 应力同时间变化曲线

由图17可知，错位系数增大，同步带带齿错位处应力增加，且传动过程中磨损程度也增加。当错位系数k=0.35时，主、从动轮啮合区后端齿根应力小幅减小，但带齿错位处应力增大幅值远大于其齿根应力减小幅值(见表3)，且磨损程度增加。故齿间错位系数k=0.00时，同步带应力分布更均匀，所受应力更小，啮合性能更好。

传动过程中，同步带带齿齿根自紧、松边与主、从动轮啮入和啮出时，同步带带齿与轮齿存在干涉，带齿受到带轮轮齿挤压作用产生形变，造成带齿齿根前端应力大于带齿齿根后端，故节点N处应力大于节点M处。

3.2.2 横向振动 图18为同步带张紧力F=400 N下，新型人字齿同步带不同齿间错位系数松、紧边横向振动幅值。由图18可知，齿间错位系数k=0.00时，同步带横向振动幅值最小，紧边振动量为1.00 mm，松边最大振动量为1.15 mm。齿间错位系数越大，带齿与轮齿啮合频率越高，导致横向振动越大。同时错位处带齿应力增大，同步带传动性能降低。

3.2.3 传动误差 由图19可知，错位系数k=0.00时，同步带传动系统角速度波动最小，传动误差最小。此外，角速度波动与横向振动振幅波动呈正相关，0.00～0.20 s为传动系统加载阶段，其中角速度峰值波动较大的原因主要是由于从动轮沿X轴方向张紧同步带导致其产生非线性转角波动。

表3 啮合区应力变化幅值(错位系数0.00～0.35)

3.2.4 干涉量波动 由图20可知，错位系数k=0.00时，同步带与带轮干涉深度及干涉速度波动量更小，即应力表现更好，传动更平稳。错位系数k=0.50时，新齿廓人字齿同步带干涉速度在0.00～0.20 s加载阶段产生较大波动的原因是错位系数变大导致带轮角速度波动变大，边界干涉频率变高。同时错位处带齿应力变大，故边界干涉变大，其干涉速度也增大。

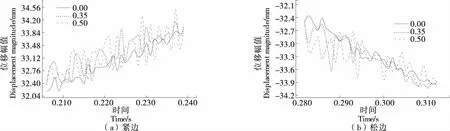
图18 松、紧边位移幅值

综上，新齿廓人字齿同步带传动系统中，外部负载条件不变情况下，同步带螺旋角β=30°，齿间错位系数k=0.00时，应力分布更为均匀，带齿受轮齿挤压作用更小，因此振动特性也更好，传动误差更小、传动更平稳。

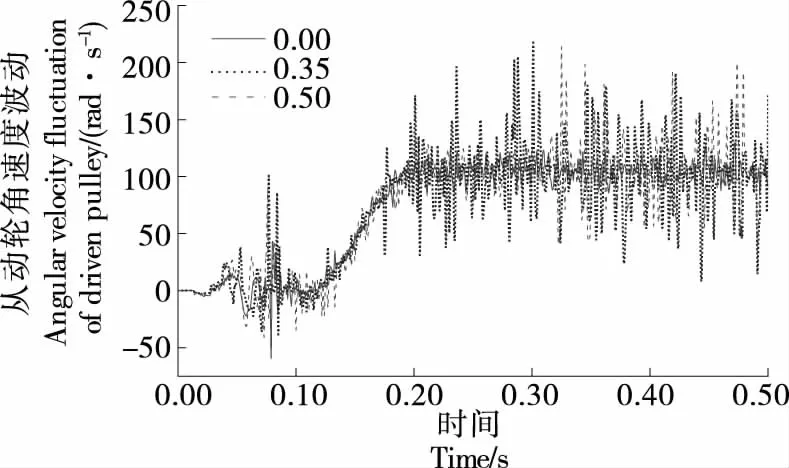
图19 从动轮角速度波动

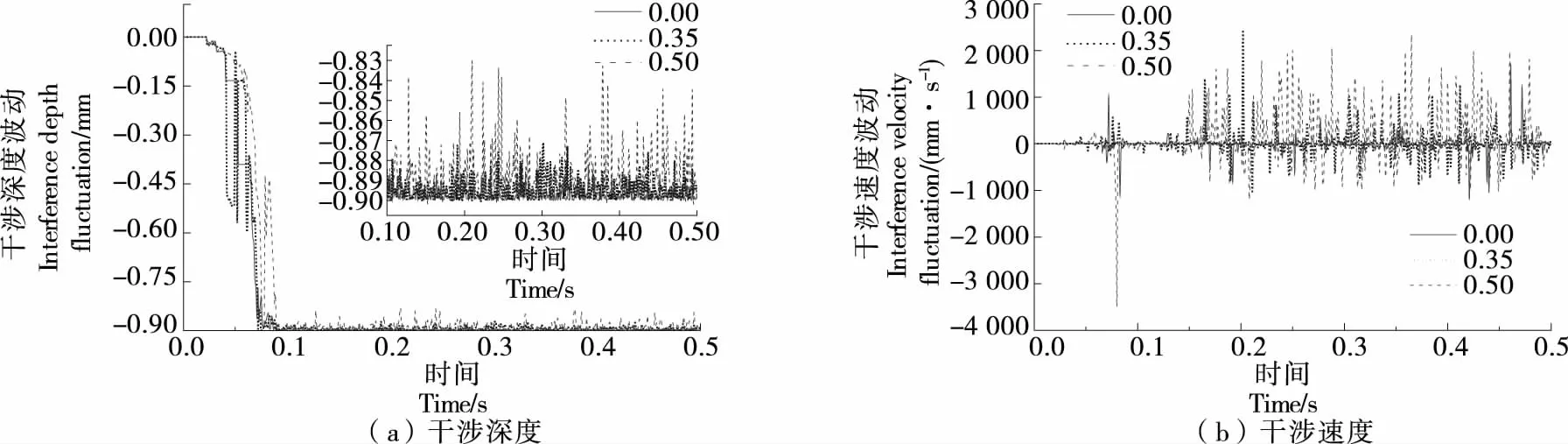
图20 干涉深度与干涉速度波动

4 结论

基于新齿廓人字齿同步带传动，对魔芋精粉机第4级传动系统进行了优化设计，采用新齿廓人字齿同步带代替传统直齿同步带传动，并在此基础上对人字齿同步带的齿形参数进行了优化，再基于刚柔耦合技术对传动系统带齿应力分布及变化与振动特性进行了动力学性能分析。结果表明：① 外部负载条件不变情况下，人字齿同步带相较于直齿同步带带齿应力更小，横向振动、传动误差更小；同步带螺旋角大，带齿齿根应力呈减小趋势；同步带齿间错位系数大，带齿齿根应力呈增大趋势。② 传动过程中，同步带带齿受到带轮轮齿挤压作用产生弹性形变，同步带带齿齿根前端区域应力大于带齿齿根后端区域。③ 当新型人字齿同步带螺旋角β=30°，齿间错位系数k=0.00时，其啮合传动过程中带齿应力更小，应力分布更均匀，横向振动振幅更小，传动更平稳，传动误差更小，干涉量波动更小，啮合特性更好。文中对同步带结构进行了简化，未能准确考虑层间性能对其啮合传动性能影响，后续将进一步对仿真模型进行优化，并结合试验分析齿廓参数及结构参数对同步带优化，以期降低传动噪声，提高传动效率。