抗逆学生问题解决能力表现的实证研究

沈启正 夏 晶

研究基于2019 年浙江省初中教育质量监测数据，探索家庭社会经济地位不同的学生在数学、科学学科中“问题解决”能力的表现。家庭社会经济背景通常指学生家长的社会经济地位和家庭的物质文化条件[1]。 家庭社会经济地位被认为是影响学生学业成就的重要因素。美国社会学家科尔曼在20 世纪60 年代就发现了学生家庭背景与学业成就的正相关性。 就整体而言，家庭社会经济地位越高，学生的学业成绩越好。但与此同时，也发现一部分家庭社会经济地位较低的学生，可以克服由此带来的不利影响，取得优异的学业成绩，这部分学生被称为抗逆学生。

问题解决能力属于高层次认知能力， 是近年来国际教育界比较关注的一种教学方法和教育思想[2]，它始于1980 年的美国，至今被人们广泛接受，成为理科教育的中心课题。 真实情景下的学习和深度学习的项目化探究，均是以问题解决能力为出发点的。

本文集中研究抗逆学生在数学、 科学学科中问题解决能力表现与其他类型学生的差异， 分析抗逆学生在问题解决各个维度中的不同表现， 以期为分析这种教学规律，为提升抗逆学生分析问题与解决问题能力提供参考。

一、研究设计

1. 抗逆界定

参考PISA 报告对“抗逆学生”和“弱势学生”的划分方式[3]，将社会经济地位在全省样本后四分之一，同时语、数、科三门学科的学业量尺分①学业量尺分是指依据学生原始作答模式将其在学科上的得分依据项目反应理论模型转化为平均分为500 分、标准差为100的量尺分，每个学科分维度转化为平均分为300、标准差为50 的量尺分数。与原始分相比，量尺分的优越性在于对不同时间、内容和难度的测试结果，可采用统一的标准进行衡量、比较。均值在本地区前四分之一的学生称为“抗逆学生[4]”；将社会经济地位处于全省后四分之一， 量尺分均分在本地区后四分之一的学生称为“弱势学生”；将社会经济地位处于全省前四分之一， 量尺分均分在本地区后四分之一的学生称为“落后学生”（因校本数过少，本文不做研究）；将社会经济地位在全省前四分之一，且量尺分均分也在全省前四分之一的高社会经济地位和高学业表现学生称为“双高学生”。

2. 研究对象

参加2019 年浙江省初中质量监测的8 年级学生共41590 名，剔除变量缺失值样本，最终有效人数38600 人，分布在城市、县镇、农村学校。 其中抗逆学生2951 名，弱势学生2849 名，双高学生2027 名。

3. 研究工具

2019 年浙江省初中教育质量监测开发了语文、数学、科学三个学科的纸笔测试卷。 语文学科主要考查阅读能力； 数学学科侧重考查 “问题解决”能力，包括信息收集与理解、计划探索与制定、方案实施与改进、结果反思与评判四个维度；科学学科侧重考查探究能力，包括提出科学问题、设计探究方案、获取和解释证据、科学解释现象、评价科学探究五个维度。

科学学科试题的“科学探究”是以问题解决为导向，数学与科学两个学科都呈现出问题新颖、内容综合、指向目标、立足能力、关注策略等特点，本研究按测试框架与命题意图，合并数学、科学两学科的相近能力维度，以数学学科的名称为主干，组成本文所称的“问题解决”能力框架，见表1。

表1 问题解决能力的分析维度

二、研究结果与分析

1. 抗逆学生总体得分情况

图1 反映了三个群体学生在数学、 科学和总的问题解决能力方面的得分率情况。 不同群体得分率存在明显差异： 抗逆学生和双高学生的得分率相接近，均远远高于弱势学生。

表2 表明针对不同类型的学生， 各类得分率均有显著差异性（P＜0.05）。

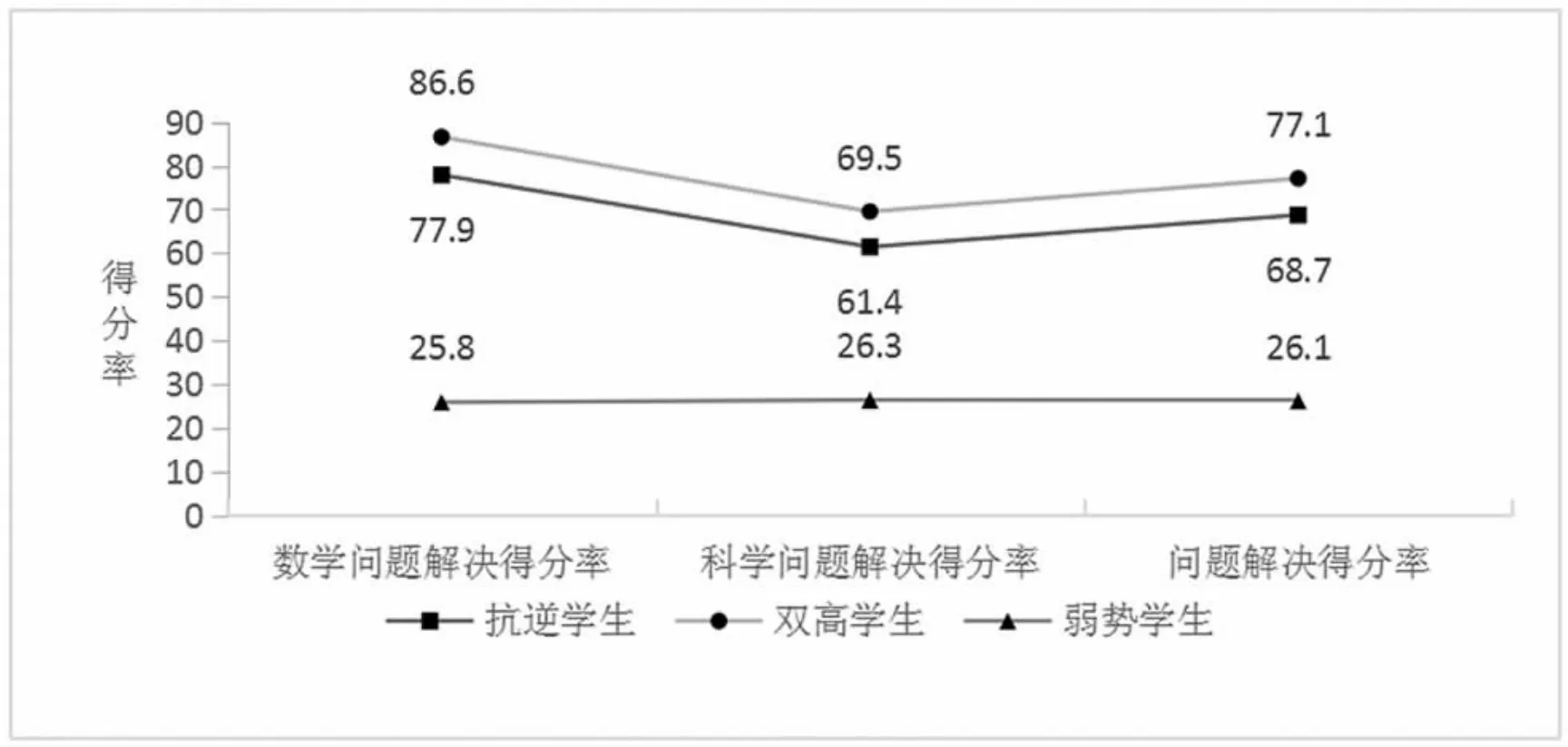
图1 问题解决得分率

表2 不同类型问题解决得分率事后检验表

图2 反映了三个群体学生问题解决能力不同维度的得分率情况。 同群体在不同维度上的得分率较为均衡，但不同群体得分率存在明显差异：抗逆学生与双高学生得分率比较接近；得分率均远远高于弱势学生。

表3 表明，在本文研究的问题解决各维度中，不同类型的学生均有显著差异性（P＜0.05）。

图2 不同类型学生问题解决维度得分率

表3 不同类型学生在问题解决维度中的事后检验表

图3 综合了图1 和图2 的内容， 纵坐标是各维度中双高与抗逆学生的得分率差值、 抗逆与弱势学生的得分率差值情况。结果显示：数学问题解决的得分率，抗逆与弱势学生差值高达52.1%，远超问题解决能力维度差值的42.7%； 而科学问题解决的得分率差值为35.1%， 比总的问题解决能力维度差值42.7%要低7.6%。 另一个值得注意的现象是：在“结果反思与评价”分维度上，抗逆与双高学生的得分率差值最小，为6.2%；“方案实施与改进”分维度差值最大，为9.7%。 说明抗逆学生在“结果反思与评价”维度上与双高学生水平比较接近，在“方案实施与改进”维度上与双高学生之间尚存在差距。

图3 不同类型学生维度得分差值

2. 各学科能力得分率的相对百分比

各科试卷难度不同，得分率相差较大，引入得分率的相对百分比， 容易看出哪个学科的问题解决能力对抗逆的作用更大， 研究纳入语文阅读的认知能力一起进行比较。

由图4 可知，抗逆与弱势学生相比，语文阅读高层次能力得分率的相对百分比为51.3%，明显低于总的问题解决的62.1%。 更显著低于数学问题解决的66.9%和科学问题解决的57.1%。而抗逆与双高学生相比，各学科的相对百分比较为接近，差异不大。 因此可以初步得出结论：抗逆学生之所以能够从弱势学生中脱颖而出，与他们数学和科学的问题解决能力较强、尤其是数学学科的优势明显有关。

本研究进一步分析了科学试题中的物理和化学部分，得到图5。

图4 得分率相对百分比示意图

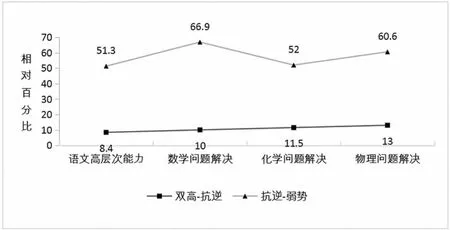
图5 相对百分比示意图

可见， 物理学科中的问题解决能力对抗逆的作用也相当大，仅次于数学学科；化学问题解决维度的得分率相对百分比与语文阅读能力则很接近。因此，数学、 物理学科的问题解决能力强是抗逆学生取得优异成绩的重要因素。

3. 问题解决各维度得分率的相对百分比

图6 是抗逆与弱势学生在问题解决各维度中得分率的相对百分比。从图中发现，问题解决的四维度中，“方案实施与改进” 维度是抗逆学生超过弱势学生最大的亮点，其次是“计划探索与制定”维度，而这两个维度正是问题解决中的核心环节， 是需要综合运用多种思维才能突破的关键难点， 确实需要学生具备创新思维。结合图7 可发现，“结果反思与评价”维度中， 无论是抗逆学生与弱势学生的相对优势还是抗逆与双高学生的相对差距， 与前两个维度相比都有很明显的压缩。 综合研究这三个维度的试题可发现，“结果反思与评价”维度较“计划探索与制定”、“方案实施与改进”维度，思维的深度与广度要求有明显的降低，弱势学生在“结果反思与评价”维度上的得分率有较大的提高。

图7 反映了双高与抗逆学生在问题解决各维度中得分率的相对百分比。可见双高与抗逆学生在“结果反思与评价”维度上比较接近，在“方案实施与改进”维度存在着12.7%的差距。

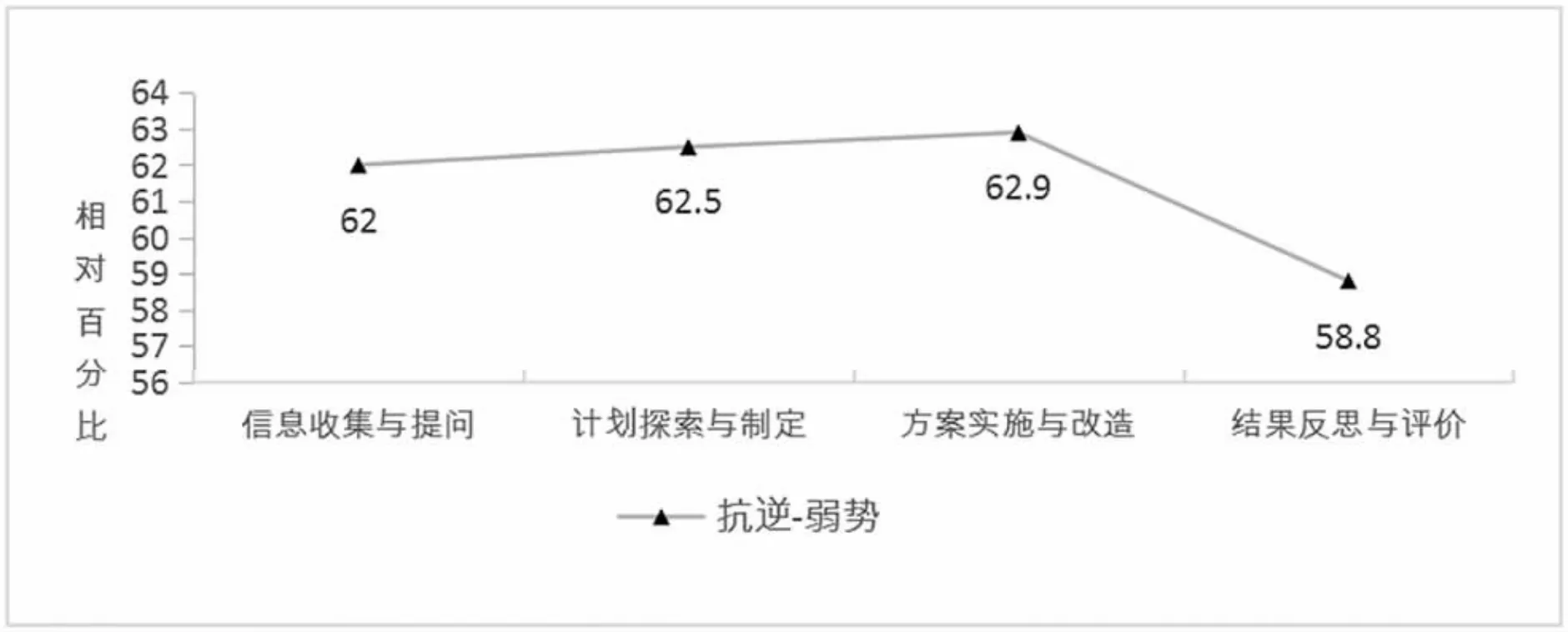
图6 抗逆与弱势学生相对得分示意图

图7 双高与抗逆学生相对得分示意图

4. 综合解决复杂问题能力的得分率差异

本次监测中，科学、数学学科的主观题都具有较新的情境，要求学生拥有足够的思维广度和深度，需要学生具备综合运用所学知识解决复杂问题的能力。 图8 是以科学和数学的主观题得分率作为学生综合解决复杂问题的能力指标。从得分率大小可知，双高与抗逆学生科学、 数学的综合解决复杂问题能力都远远高于弱势学生；从三条图线的斜率可知，抗逆学生与双高学生科学、 数学得分率组成的斜率几乎相同，但弱势与抗逆学生则差距明显，反映抗逆学生在数学综合解决复杂问题能力上相对于弱势学生优势更加明显。

5. 男女抗逆学生的总体情况分析

本次监测中，抗逆学生共2951 名，其中，男生1601 名，占54.3%，女生1350 名，占45.7%。 图9 为男、女生抗逆生问题解决维度的得分率情况。可以发现男、女生问题解决能力总体比较接近，女生在科学问题解决中略为占优，但差别不大。

图10 为不同性别抗逆学生在问题解决各维度中的得分率情况，可见男、女生总体比较接近，女生略占在“计划探索与制定”维度上优势略明显，但女生也仅比男生高1.5%。

图8 复杂问题得分率示意图

图9 不同性别抗逆学生得分率示意图

图10 不同性别学生问题解决维度得分示意图

三、典型试题分析

以下选取典型试题具体考察抗逆学生与其他类型学生在问题解决中的表现情况。

典型题1：如图，有两个全等的直角三角形硬纸片，它们的两条直角边分别为2 和4。用这两个纸片可拼出各种不同的四边形，画出所有符合要求的四边形。（此处四边形不包含凹四边形。）

图

本题的解题过程包含了问题解决的全部维度：着重考查了信息收集与提问、计划探索与制定这两个维度。 按照SOLO 理论评分，学生答题共有18 种情况。 图12 的横坐标是不同的得分值，纵坐标是相应的人数百分比。

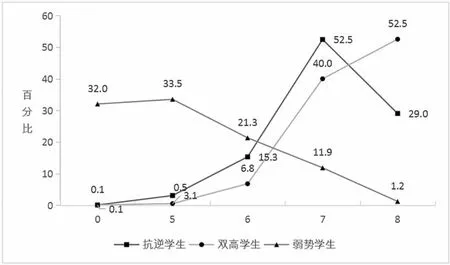
图12 不同得分的人数百分比

图12 揭示，弱势学生得0 分的高达32%，得5分的人数最多，占33.5%；抗逆学生得7 分的人数最多，占52.5%。抗逆学生在平均约6.2 分以上时，各分数的人数百分比均超过弱势学生，7 分时与弱势学生拉开了最大的差距， 人数百分比差值达到了40.6%， 达满分8 分的人数百分比则比弱势学生高近28%。 可见抗逆学生的思维严密性与深刻度要远胜弱势学生。 双高学生得满分8 分的人数最多，占52.5%， 抗逆学生得5-7 分的人数百分比均超过了双高学生；但得满分8 分的人数百分比则比双高学生少23.5%。三类学生的人数峰值分别出现在5 分、7 分和8 分，根据项目反应理论（IRT）得到的能力值（下简称为能力值），得5 分的学生能力值为-1.94，得7 分的能力值为-0.52， 得8 分学生能力值为1.43，能力值区间范围为[-3，3]。 也就是说大多数弱势学生的能力值位于[-3，-1.9]之间，大多数的抗逆学生的能力值位于0 左右，大多数双高学生的能力值位于1.4 附近。可见在难度值要求较高时，抗逆学生会被双高学生拉开一些距离，说明抗逆学生与双高学生相比，思维的严密性和深刻性仍存在着差距。

典型题2：为观测水结冰的过程，某同学进行如图的实验：在小试管中倒入适量的水，在水中插入并固定温度计，再将此小试管放入加有食盐的碎冰中冷却，每隔1 分钟记录温度计的示数及小试管内水的状态，结果如下表。

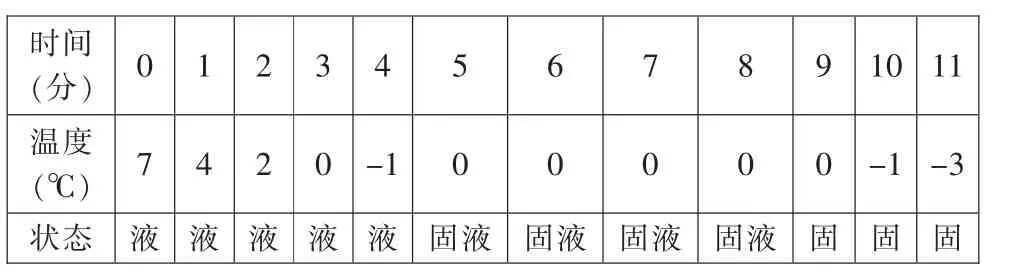
时间（分） 0 1 2 3 4 5 6 7 8 9 10 11温度（℃） 7 4 2 0 -1 0 0 0 0 0 -1 -3状态 液 液 液 液 液 固液 固液 固液 固液 固 固 固

（1）请根据表中数据在下面方格中画出小试管内水的温度随时间变化的关系图像。

（2）根据表中数据，某同学认为冰是晶体，你是否赞同?

（3）针对上小题的回答，说明理由。

本物理题全面考查了问题解决中的 “信息收集与提问、计划探索与制定、方案实施与改进、结果反思与评价”这四个维度。 按照SOLO 理论，第（1）小题采用4 级评分，第（2）小题采用2 级评分，第（3）小题采用4 级评分。

根据项目反应理论（IRT）得到的难度值，第（1）小题得1 分对应难度值-1.34；得2 分对应难度值-1.26；得3 分对应难度值0.48；难度值区间范围为[-3，3]。 由图13 可知， 双高学生得3 分的人数比例为60.5%，抗逆学生为51.4%，均为各自的最多人数，而弱势学生得3 分的仅为8.1%， 弱势学生最多人数比例出现在2 分处，为36.7%，另一个高峰位于0 分处，高达35.4%，即1/3 弱势学生得0 分；可见本小题由于得满分对应的能力值仅为0.63，难度不大，抗逆学生与双高学生差距不明显，但抗逆学生与弱势学生相比，得满分的学生数百分比几乎是弱势学生得0 分和1 分的人数总和。

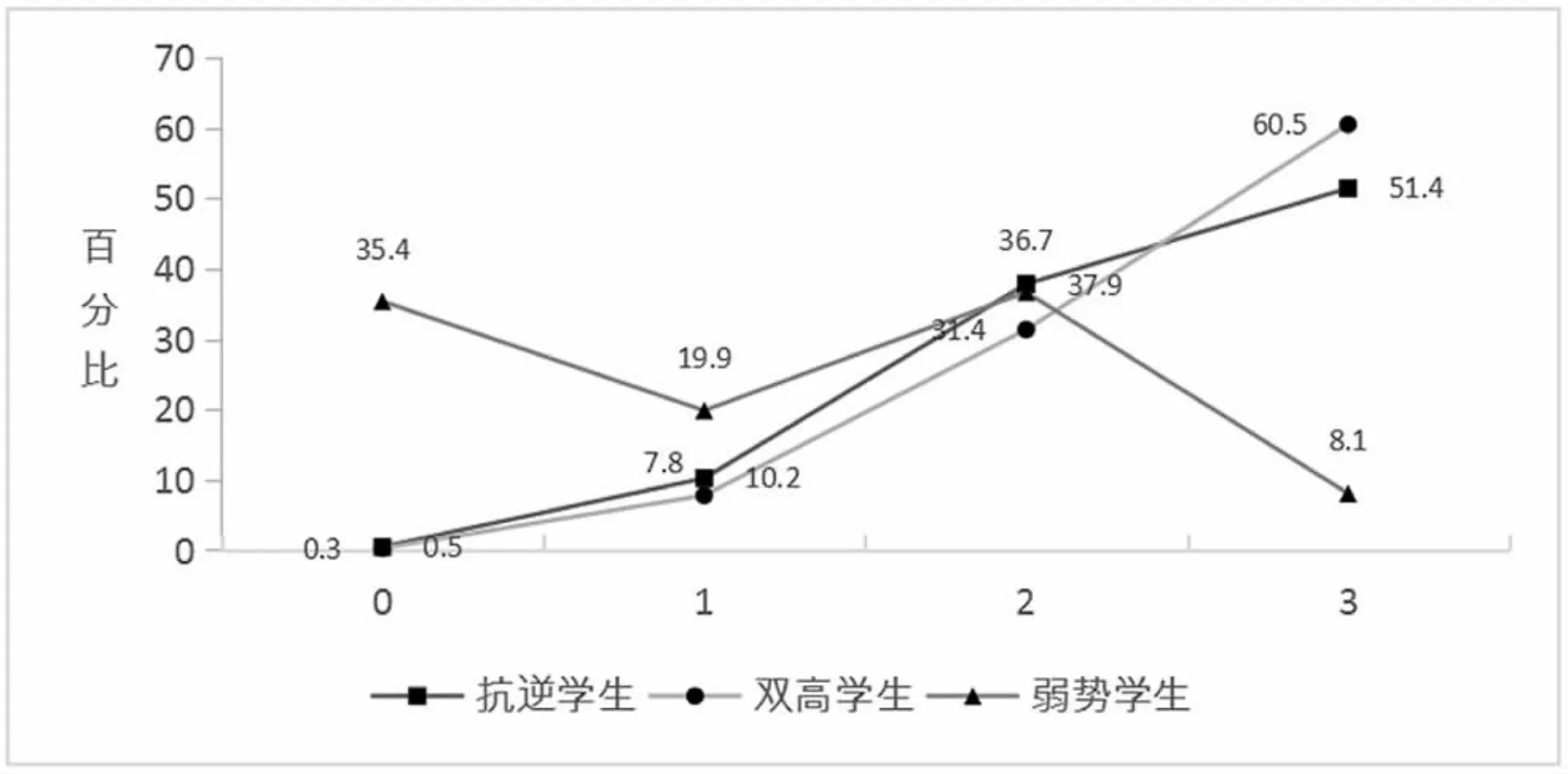
图13 不同得分人数百分比

第（2）小题得2 分对应的难度值为0.38，考查问题解决中的“结果反思与评价”环节，答案唯一。 但学生的得分率不高。 图14 反映出双高学生有59.9%得满分，而抗逆学生有45.7%、弱势学生有37.9%得满分。 这个比例看来差距不是很大，但这是二选一的判断填空题，可能存在着一定的猜测成分。

图14 不同得分人数百分比

第（3）小题得1 分对应难度值2.37；得2 分对应难度值2.89；得3 分对应难度值3.38。 这是难度相当大的问题，三类学生的错误率均极高。 本小题4 级评分。 由于要得满分需要三段论严谨推理，故只有17.5%的双高学生、8.3%的抗逆学生和0.9%的弱势学生得1 分，得2 或3 分的学生就很少了。 不过值得注意的是在难度值达到2.37 的情况下，双高学生的人数百分比超过了抗逆学生近一倍，说明双高学生中的顶尖学生比例大幅超过抗逆学生，如图15。

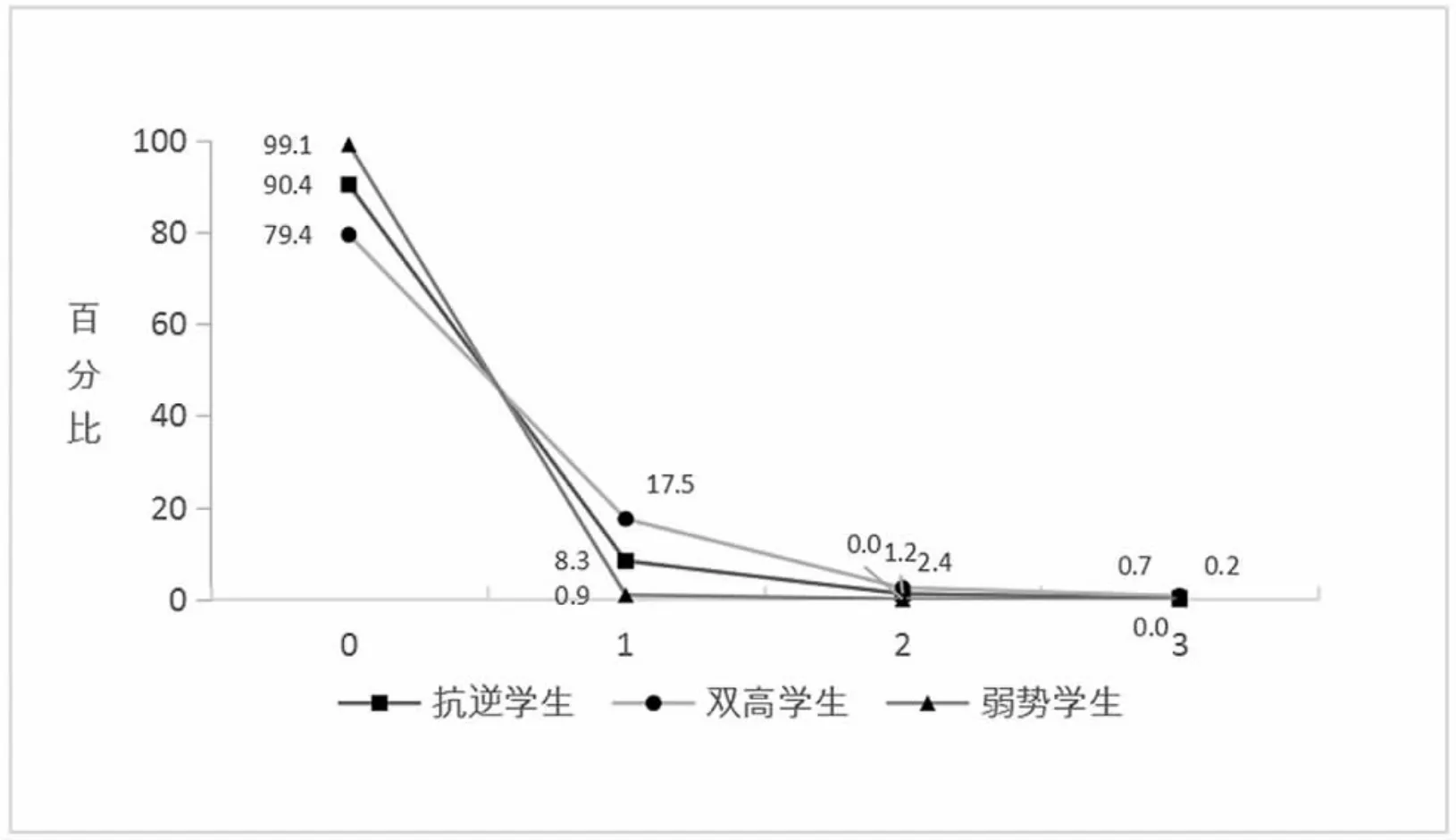
图15 不同得分人数百分比

典型题3：某科学小组为了测量容器中氧气的含量随可燃物燃烧的变化情况，利用如图中甲所示的实验装置，进行了如下操作：用相同规格的集气瓶收集三瓶空气，依次标为A、B、C；分别往燃烧匙里加入足量的红磷，使红磷依次处于图乙所示标注处；密闭容器并点燃红磷，直至熄灭一段时间后；其中红磷位于图17 乙“2”处时，图像显示仪显示的容器内氧气含量随时间变化图像如图17 丙所示。

（1）将红磷分别置于图乙标注的三个位置进行测量，其目的是_____。

（2）由图丙可得出的结论是_____。

（3）请针对燃烧后容器内最终的氧气含量提出一个适合进一步探究的科学问题。

本化学题着重考查问题解决中的“方案实施与改进、结果反思与评价”这两个维度。 按照SOLO 理论，第（1）小题采用4 级评分，第（2）小题采用2 级评分，第（3）小题采用4 级评分。 从基于IRT 模型的难度值来看，难度相当大，各小题的最高难度值均超过3 。

第（1）小题对应的难度值，得1 分为1.19、得2分为2.72、得3 分为4.78。 从图16 可知，90.1%的弱势学生、62.7%的抗逆学生和49.8%的双高学生均得0 分。对比得1 分的人数，抗逆学生占比为33.2%，双高学生占比为44.7%，但弱势学生仅占8.8%，明显弱于抗逆学生。得2 分和3 分的学生更少，全省得3 分的只有27 人，缺乏统计意义。

第（2）小题对应的难度值，得1 分为0.10、得2分为2.11、得3 分为4.63；本题得0、1、2 分的区分度很高， 抗逆学生与双高学生在0、1 得分中区分不明显， 得2 分时双高学生人数百分比约为抗逆学生一倍，但弱势学生得2 分的极少。得3 分的情况因为人数太少，已无统计对比的意义，如图17。

第（3）小题对应的难度值，得1 分为1.64、得2 分为2.12、得3 分为3.07。 从图18 可知，大多数学生得0分，18%的双高学生得1 分，13.6%的抗逆学生得1 分，2.5%的弱势学生得1 分。 而得2 分或3 分时，双高学生的人数百分比（1.5%）约是抗逆学生（0.8%）的一倍。

图16 不同得分人数百分比示意图

图17 不同得分人数百分比示意图

四、启示与反思

1. 数理能力强是抗逆学生展示学业水平的重要因素

本次监测数据表明， 抗逆学生与弱势学生数学问题解决的得分率差值最大， 其次是科学中的物理学科，这两者都远高于语文和化学等学科。学习的客观条件有所制约，但逻辑思维能力强、数理推理能力佳的学生仍有可能摆脱自身社会经济地位弱势的影响，在数学和物理这两门需较强逻辑思维推理、却不需要太多资源支撑学习的学科中展示较好水平。

2. 抗逆学生在方案实施与改进维度的能力更强

从问题解决能力的四个维度的数据分析可知，“方案实施与改进”维度是抗逆学生超过弱势学生最大优势，其次是“计划探索与制定”维度。这两个维度是问题解决的核心能力， 是需要综合运用多种思维能力才能解决问题的关键突破点。数据还显示“结果反思与评价”是抗逆学生与弱势学生相对优势收敛的维度。可见，问题解决的难度制高点在“方案实施与改进”这一维度上，难度次高点则是“计划探索与制定”维度。

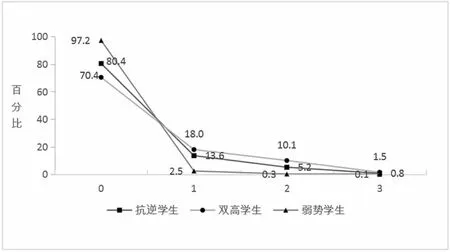
图18 不同类型学生得分百分比

3. 抗逆学生与双高学生总体存在一定差距

无论从数学和科学问题解决的得分率来看，还是从四个维度的分项得分率来研究， 抗逆学生与双高学生的图线都近乎于平行折线， 存在着较稳定的基础背景式“能级差”。 抗逆学生社会经济地位的制约，存在着学习背景、教育资源等差异，因此在初二阶段暂时出现在问题解决能力上的“能级差”也是正常的。随着学习的深入和阅历的增加，相信这样的差距总体上会有所弥补。

4. 双高学生比抗逆学生拥有更多尖子生

从学生解决各学科复杂问题的实例分析可知，在基于IRT 模型的难度值小于零或约等于零时，抗逆学生得分的人数百分比超过了双高学生得分的人数百分比；当基于IRT 模型的难度值位于1 附近时，抗逆学生与双高学生得分率均下降明显， 两者存在着一定差距；当基于IRT 模型的难度值大于2 时，两者的得分率显著大幅减小，并且二者的差距增大。究其原因，当试题难度在中等或以下时，无论是抗逆学生还是双高学生， 学业成绩均处于群体中的前1/4，故差距不大。 但当难度更大时，处于群体中前1/4 的学生也大部分均无法应对， 只能少数顶尖学生才能答对，这时若双高学生中尖子生比例高，就会与抗逆学生拉开距离。

5. 男女抗逆学生总体差异情况不明显

抗逆学生性别比例男生略多于女生， 占比分别为54.3%和45.7%。 无论是在科学还是数学学科，男女抗逆学生在问题解决的得分率上十分接近， 女生略好于男生， 综合解决复杂问题的能力两者也十分接近。在问题解决各维度中女生略有优势，但总体上差异较小，在差异最大的“计划探索与制定”维度，女生也仅比男生得分率高1.5%。 可见性别不是阻碍抗逆的决定因素。

近年来，随着基于核心素养的课程改革的深入，对于问题解决能力的研究， 更多着眼于学校教育和课堂教学。但也应该清醒认识到，学生问题解决能力的培养是个渐进的过程，是终身学习的目标。由于此能力的综合性，学生成长环境对它的影响大。因此研究抗逆学生在解决问题中的能力表现， 有利于我们进一步了解抗逆学生的成功机制， 有助于我们思考学生成长的本质， 有益于我们降低不必要的教育成本，对各类学生的成长都有着重要的意义。