一道数学考研试题的探讨

戴立辉， 黄建吾， 黄 锋

(闽江学院 数学与数据科学学院，福州350108)

1 引 言

2013年全国硕士研究生入学考试数学一、二中均有如下试题.

试题设奇函数f(x)在[-1，1]上具有二阶导数，且f(1)=1，证明：

(i)存在ξ∈(0，1)，使得f′(ξ)=1；

(1)

(ii)存在η∈(-1，1)，使得f″(η)+f′(η)=1.

(2)

此试题的解答可参考文献[1].受文献[2]的启发，本文将从试题结论的推广、相关新的结论等方面对该试题进行探讨.

2 推 广

由上述试题知，f(x)在[-1，1]上为奇函数，故由f(1)=1知f(0)=0，f(-1)=-1.但反之，若f(x)满足：f(0)=0，f(1)=1，f(-1)=-1，则f(x)未必一定是奇函数.以下将在此相对较弱的条件下对试题进行探讨.

首先给出试题的推广.

试题推广设函数f(x)在[-1，1]上具有二阶导数，且f(0)=0，f(1)=1，f(-1)=-1，若n≥0为自然数，λ为任意实数，则

(i) 存在ξ∈(0，1)，使得

f′(ξ)=1-λ+λ(2n+1)ξ2n；

(3)

(ii) 存在η∈(-1，1)，使得

f″(η)+f′(η)=λ(2n+1)η2n-1(η+2n).

(4)

证令φ(x)=f(x)-λx2n+1，-1≤x≤1，则φ(x)在[0，1]上可导，故由Lagrange中值定理知，存在ξ∈(0，1)，使得

φ(1)-φ(0)=φ′(ξ)，

而φ(0)=0，φ(1)=1-λ，φ′(x)=f′(x)-λ(2n+1)x2n，故可得

f′(ξ)=1-λ+λ(2n+1)ξ2n.

(3)

同理，由φ(0)=0，φ(-1)=-(1-λ)及Lagrange中值定理知，存在ξ0∈(-1，0)，使得

φ(0)-φ(-1)=φ′(ξ0)，

即

(5)

由式(3)，(5)知

(6)

再令ψ(x)=[f′(x)-λ(2n+1)x2n]ex，-1≤x≤1，则由式(6)知ψ(ξ)=ψ(ξ0)=0，又ψ(x)在[-1，1]上可导，故由Rolle定理知，存在η∈(-1，1)，使得ψ′(η)=0，而

ψ′(x)=[f″(x)-2λn(2n+1)x2n-1]ex+[f′(x)-λ(2n+1)x2n]ex，

且ex>0，故有

f″(η)+f′(η)=λ(2n+1)η2n-1(η+2n).

(4)

特别地，在式(3)，(4)中取λ=1，n=0即可得到式(1)，(2)，因此式(3)，(4)是式(1)，(2)的推广.

3 若干新的结论

结论1设函数f(x)在[-1，1]上具有二阶导数，且f(0)=0，f(1)=1，f(-1)=-1，若n≥0为自然数，λ为任意实数，则存在μ∈(-1，1)，使得

f″(μ)=2λn(2n+1)μ2n-1.

(7)

证由前面的式(6)知

(6)

其中0<ξ<1，-1<ξ0<0.

由于f(x)在[-1，1]上二阶可导，故对函数h(x)=f′(x)-λ(2n+1)x2n在[ξ0，ξ]上运用Rolle定理知，存在μ∈(ξ0，ξ)⊂(-1，1)，使得h′(μ)=0，即

f″(μ)=2λn(2n+1)μ2n-1.

(7)

注 由于n≥0为自然数，λ为任意实数，因此由式(7)可得出许多关于f(x)的结论.

例如，取λ=0，则由式(7)知，存在μ∈(-1，1)，使得

f″(μ)=0.

(8)

由于μ∈(-1，1)，故|μ|≤1，从而由式(7)知，存在μ∈(-1，1)，使得

|f″(μ)|≤2n(2n+1)|λ|.

(9)

由λ的任意性，令2n(2n+1)|λ|=|λ0|，则由式(9)可知，对任意实数λ0，存在μ∈(-1，1)，使得

|f″(μ)|≤|λ0|.

(10)

当然，由式(10)也可知式(8)成立，或式(10)是式(8)的推广.

结论2设函数f(x)在[-1，1]上具有二阶导数，且f(0)=0，f(1)=1，f(-1)=-1，则在(-1，1)内存在不同的两点μ1，μ2，使得

f′(μ1)=f′(μ2).

(11)

证由Lagrange中值定理知，存在μ1∈(-1，0)，μ2∈(0，1)，使得

1=f(0)-f(-1)=f′(μ1)， 1=f(1)-f(0)=f′(μ2).

故由以上两式知f′(μ1)=f′(μ2)，即式(11)成立.

注 由式(11)及Rolle定理又可得到式(8).

结论3设函数f(x)在[-1，1]上具有二阶导数，且f(0)=0，f(1)=1，f(-1)=-1，则

(i) 在(-1，1)内存在两个不同的点ξ1，ξ2，使得

f(ξ1)+f(ξ2)=-ξ1-ξ2；

(12)

(ii)在(-1，1)内存在四个不同的点η1，η2，η3，η4，使得

f′(η1)f′(η2)=f′(η3)f′(η4).

(13)

证令u(x)=f(x)+x+1，-1≤x≤1，则u(-1)=-1<0，u(0)=1>0，由连续函数的零点存在定理知，存在ξ1∈(-1，0)，使得u(ξ1)=0，即

f(ξ1)=-ξ1-1.

(14)

由Lagrange中值定理知，存在η1∈(-1，ξ1)，η2∈(ξ1，0)，使得

f(ξ1)-f(-1)=(ξ1+1)f′(η1)，f(0)-f(ξ1)=-ξ1f′(η2).

利用式(14)得

故有

f′(η1)f′(η2)=1，

(15)

其中-1<η1<η2<0.

再令v(x)=f(x)+x-1，0≤x≤1，则v(0)=-1<0，v(1)=1>0，从而存在ξ2∈(0，1)，使得v(ξ2)=0，即

f(ξ2)=1-ξ2.

(16)

由式(14)、(16)可得

f(ξ1)+f(ξ2)=-ξ1-ξ2，

(12)

其中-1<ξ1<0<ξ2<1.

再由Lagrange中值定理知，存在η3∈(0，ξ2)，η4∈(ξ2，1)，使得

f(ξ2)-f(0)=ξ2f′(η3)，f(1)-f(ξ2)=(1-ξ2)f′(η4).

利用式(16)得

故有

f′(η3)f′(η4)=1，

(17)

其中0<η3<η4<1.

由式(15)，(17)即得

f′(η1)f′(η2)=f′(η3)f′(η4)，

(13)

其中-1<η1<η2<η3<η4<1.

结论4设函数f(x)在[-1，1]上具有二阶导数，且f(0)=0，f(1)=1，f(-1)=-1.

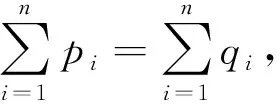
(18)

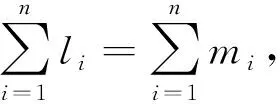
(19)

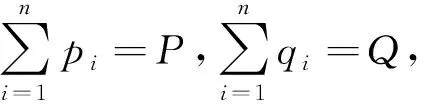
在[xi-1，xi]上对f(x)运用Lagrange中值定理知，存在ξi∈(xi-1，xi)，使得

上式对i从1到n求和，得

即

(20)

其中-1<ξ1<ξ2<…<ξn<0.

同理可得

即

(21)

其中0<η1<η2<…<ηn<1.

-1=y0

取x0=-1，xn=0，在[-1，0]上对连续函数f(x)运用介值定理知，存在x1∈(-1，0)，使得f(x1)=y1.在[x1，0]上对f(x)再运用介值定理知，存在x2∈(x1，0)，使得f(x2)=y2.依次下去，可得x3

在每个小区间[xi-1，xi]上对f(x)运用Lagrange中值定理知，存在λi∈(xi-1，xi)，使得

yi-yi-1=f(xi)-f(xi-1)=f′(λi)(xi-xi-1)，

从而

或

上式对i从1到n求和，得

(22)

其中-1<λ1<λ2<…<λn<0.

作上述类似的处理，可得

(23)

其中0<μ1<μ2<…<μn<1.

4 应 用

文中的结论有很多应用，限于篇幅，仅举一例予以说明.

例1设函数f(x)在[-1，1]上具有二阶导数，且f(0)=0，f(1)=1，f(-1)=-1，λ0为任意实数，证明方程x2f″(x)+4xf′(x)+2f(x)=λ0x3在(-1，1)内至少有一个根.

证令g(x)=x2f(x)，则g(x)在[-1，1]上具有二阶导数，且g(0)=0，g(1)=1，g(-1)=-1.

在结论1的式(7)中用g(x)代替f(x)并取n=2，由于g″(x)=x2f″(x)+4xf′(x)+2f(x)，因此存在μ∈(-1，1)，使得

μ2f″(μ)+4μf′(μ)+2f(μ)=20λμ3.

由λ的任意性，故对实数λ0，有

μ2f″(μ)+4μf′(μ)+2f(μ)=λ0μ3.

所以方程x2f″(x)+4xf′(x)+2f(x)=λ0x3在(-1，1)内至少有一个根.

5 结 论

对已有结论的条件进行弱化处理后，讨论是否仍具有原来的结论并考虑其推广，这将会使得我们的研究更加深入透彻.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.