一类广义B-T方程边值问题解的存在性
2021-05-07刘筱玥
刘筱玥, 江 滟, 邵 悦
(扬州大学 数学科学学院,江苏 扬州225002)
1 引 言
(1)
的mild解的存在性,其中Dα表示α阶Riemann-Liouville分数阶导数,Iγ表示γ阶黎曼-刘维尔型的分数阶积分,f∶[0,1]×→定义为特定函数,它符合相应条件.
阶为分数的微积分是由经典整数阶微积分推广而来,在记忆和遗传材料,流变学和力学系统,高分子材料等物理化学领域都有着广阔的现实价值.在非整数阶的微积分理论不断开拓创新的大背景下,阶为分数的微积分已经成为数学界研究的热点.文献[1]在Banach空间中讨论了非线性分数阶微分方程边值都为零的情况下解是否存在的问题.
本文旨在讨论特定的非线性的分数阶的微分方程在其边值不等于零时解是否存在的问题,设微分方程及其边值为(1)式.综合运用Schauder不动点定理等,尝试讨论f在一些比较弱的条件下,边值问题(1)的适度解是否存在,例如条件为:Caratheodory型条件等.由于当函数的初始值非零时,Riemann-Liouville分数阶导数的奇异性带来困扰,因而初始值非零的情形并非对初始值为零的简单推广.
2 预备知识
定义1[2]设h∈L1([a,b];),α>0,定义算子)→C([a,b];)为

定义2[2]设h∶[a,b]→,α>0,n=[α]+1,定义
则上式叫h在t点的α阶Riemann-Liouville分数阶导数, 式子中的[α]是指实数α的整数部分.
根据Riemann-Liouville分数阶积分的定义,能够推导得到,算子I对指标满足半群性质,也就是说,对于α,β>0,t∈[a,b],有
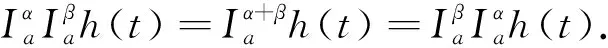
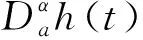
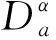
引理1[2]若Dαu∈L1([0,T];),n-1≤α 为讨论边值问题(1)解的定义,先讨论相应的线性方程.设g∈C([0,1];),α∈(1,2),β∈(0,1).考虑分数阶线性微分方程边值问题 方程两边作用积分算子Iα,得 IαDαu(t)=aIαDβu(t)-Iαg(t). (2) 由于1<α<2,由引理1知,存在常数c1,c2,使得 IαDαu(t)=u(t)+c1tα-1+c2tα-2. (3) 由α阶Riemann-Liouville分数阶积分的性质得 IαDβu(t)=Iα-βIβDβu(t). (4) 由于0<β<1,由引理1知,存在常数c3,使得 IβDβu(t)=u(t)+c3tβ-1. (5) 将(5)式代入(4)式得 IαDβu(t)=Iα-βu(t)+c3Iα-βtβ-1. (6) 代入(6)式得 (7) 将(3),(7)式代入(2)式,得 化简后得 上式两边应用积分算子I2-α,得 (8) 即 (9) 令 (10) 则(9)式可化为 (11) 在此基础上,到了边值问题(1)对应的mild解,并给出定义3. 则称u是边值问题(1)的一个mild解,其中P,G1,G2由(10)给出. 记空间C2-α(0,1]={x:(0,1]→|x连续且存在}.定义范数为 于是此作出以下假设 (T1)f(0,1]×→,符合Caratheodory条件,也就是对于几乎处处t∈(0,1],f(t,·):→连续;对于u∈,f(·,u):(0,1]→可测. (T2) ∃h∈Lp((0,1];+),Ω∶(0,+∞)→(0,+∞)非减局部有界,使得∀t∈(0,1],x∈X,有 |f(s,u(s))|≤h(s)Ω(‖u‖), 且 定理1若(T1)、(T2)成立且k1<1,则边值问题(1)有解. 证定义算子T∶C2-α(0,1]→C2-α(0,1],为 那么容易看出T的不动点就会成为满足边值问题(1)的mild解.下面用Schauder不动点定理来辅助证明t2-αTu(t)在题设范围内存在不动点. 显然,通过条件(T1), (T2)以及辅助应用控制收敛定理,可以知道T连续. 下一步,要证明有界闭凸集U⊂B,0∈U的存在,可以使之满足TU⊂U,事实是可以证明,由(T2),有 因此可取r>0,使得 从而有 Ω(r)k2‖h‖p+k3+rk1≤r. (12) 记U={u∈C2-α(0,1]∶‖u‖≤r},则显然U是C2-α的有界闭凸集,对∀u∈U,t∈(0,1], 由(T2)及(8)式,利用赫尔德不等式,可得 ≤k3+rk1+Ω(r)‖h‖pk2≤r. 由上面可以推导出t2-αTU⊂U.而且也容易得到t2-αTU一致有界. 下一步需要证明T映C2-α中有界集为等度连续集.首先需要假设U⊂C2-α为有界集,则存在r>0,使得∀u∈U,有‖u‖≤r,任取t1,t2∈(0,1],设t2>t1,则 =I1+I2+I3+I4+I5. (13) 由于 (14) 由于α∈(1,2),β∈(0,1),利用积分的绝对连续性,由(9)-(14)式可得当t2-t1→0时 因此t2-αT映C2-α中有界集为等度连续集. 至此,证明了t2-αT是连续的,映有界集为等度连续集,从而t2-αT为连续的紧映射,即满足Schauder不动点定理,因此t2-αT不动点的存在性得以证明, 亦即T不动点的存在性也得以证明,故边值问题(1)mild解的存在性已证明完毕.定理得证. 进一步地,定理1中的增长性条件(T2)完全可以由下面的次线性增长替换. (T3) 存在a1,a2∈Lp([0,1]∶+),使得|f(t,u(s))|≤a1(t)+a2(t)‖u‖,∀t∈(0,1],x∈X. 为方便起见,以下记: 定理2若(T1), (T3)成立,且0 证此定理的证明与定理1的证明非常类似,首先需要定义一个算子T:B→B ≤N3+rN1+N2. 由r的取法可知,N3+rN1+N2≤r,故得‖Tu‖≤r.因此,TU∈U.从以上证明中易见TU一致有界.下面证Tu等度连续.由前证知Tu有界,任取t1,t2∈[0,1],t1 其中 由此易知,t2-αT映C2-α中有界集为等度连续集. 到这里,已经完成了证明了t2-αT连续性的证明,以及满足映有界集为等度连续集的条件,从而t2-αT为连续的紧映射,并且使之可以符合应用Schauder不动点定理的条件,从而得知t2-αT在题设区间内不动点的存在性,也就是说T存在不动点,故存在满足边值问题(1)的mild解.至此,定理证明完毕. 本文研究了一类广义的Bagley-Torvik方程的边值问题解的存在性.讨论是边值非零的情形.由于Riemann-Liouville分数阶导数当初始值非零时具有弱奇异性,因此讨论的问题并非齐次边值问题的简单推广.首先讨论相应的线性方程,由此得到此类问题的Green函数,给出mild解的定义.在加权的连续函数空间中,利用Schauder 不动点定理,证明了边值问题(1)的mild解存在的充分条件. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.3 mild解的存在性
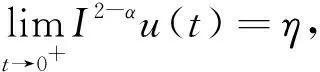
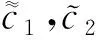

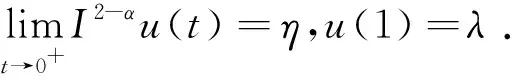





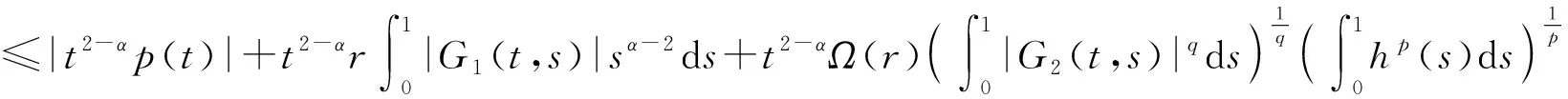
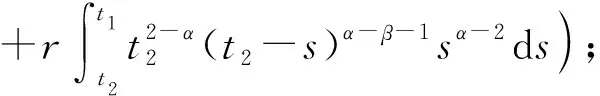

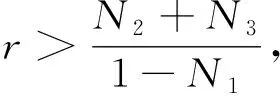



4 结 论
