关于Hardy型不等式的讨论

周烁星， 楼红卫

(复旦大学 数学科学学院，上海200433)

1 引 言

在一些习题集中，有如下有趣的问题：

例1很自然地可以推广到其他幂平均的情形.对于整数n≥1和实数α，来定义非负数列a1，a2，…，an的幂平均.

首先，若α>0，或α<0且a1，a2，…，an>0，则定义

(1)

若α<0，且a1，a2，…，an至少一个为零，则令Mα(a1，a2，…，an)=0.

最后，定义

(2)

易见Mα(a1，a2，…，an)关于α∈(-∞，+∞)以及a1，a2，…，an都是单调增加的.自然地，将例1一般化为如下命题.

证(i) 由幂平均的单调性，不妨设0<α<1.由Hölder不等式，有

从而

(3)

为讨论连续性的问题，对于实数α以及[0，+∞)上非负可积函数f，来定义函数f的幂平均函数Mα(f).设x>0.

若α>0，或α<0且f有正下界，则直接定义

(4)

对于α<0 但f不一定有正下界，用下式定义

(5)

类似地，对于α=0，定义

(6)

类似于Mα，Mα(f)关于α单调增加.当f，g非负可积且f≥g时，Mα(f)≥Mα(g).

例1有以下连续型的推广.

证(i) 由幂平均的单调性，不妨设0<α<1.由Hölder不等式，有

因此

(7)

2 离散型结果的一般化

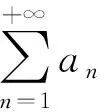
为方便起见，引入如下定义.

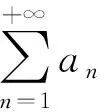
有如下命题.

命题2设g∶[0，+∞]→[-∞，+∞]连续且严格单调.若k≠0，b∈(-∞，+∞)，则f∶=kg+b也是 [0，+∞]映到[-∞，+∞]的严格单调函数.则对任何非负实数列a1，a2，…，an成立

特别地，此时f具有性质PD当且仅当g具有性质PD.

由此即得命题.

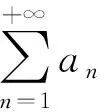
证必要性显然.只需要证明充分性.

不妨设f严格单调递增，否则由命题2，考虑-f即可.

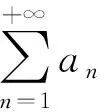
f(b1)+f(b2)+…+f(bN)≤Nf(δ).

命题3表明f是否具有性质PD只与它在0点附近的取值有关.作为其推论，易得如下命题.

命题4设f，g∶[0，+∞]→[-∞，+∞]均连续且严格单调，f具有性质PD.若存在正常数C1，C2，δ使得对于x∈(0，δ)成立f(C1x)≤g(x)≤f(C2x)，则g也具有性质PD.

命题5设f∶[0，+∞]→[-∞，+∞]，g∶[-∞，+∞]→[-∞，+∞]均连续且严格单调，f具有性质PD.进一步，设以下条件之一成立: (i)f单增，g-1凸; (ii)f单减，g-1凹.则g∘f也具有性质PD.

证对于非负数列{an}，有

由此即得g∘f也具有性质PD.

提请读者注意，在g∶[-∞，+∞]→[-∞，+∞]严格单调的前提下，g-1凸当且仅当g凹且单增或g凸且单减.而g-1凹当且仅当g凸且单增或g凹且单减.

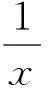
3 连续型的进一步推广

类似于定义1，引入如下定义.

仿命题3，可以建立如下命题.

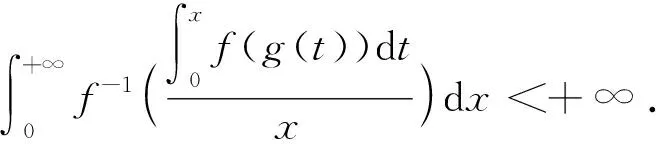
以下命题给出了性质PD与PC之间的等价性.

命题7设f∶[0，+∞]→[-∞，+∞]严格单调.则f具有性质PD当且仅当在f具有性质PC.

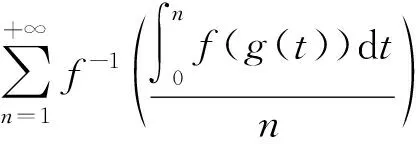
4 结 语

从一个收敛的正项级数出发，引入由级数的一般项的各种平均产生的新的一般项，考察新的级数的收敛性.类似问题曾经由著名数学家 Hardy 加以研究并得到优美的结果.本文将有关结果推广到更广泛的情形，同时对一些特例简化了证明.文章较好地体现了发现问题并逐步深入研究最终得到一些有意义的成果的过程.

致谢本文受益于复旦大学数学科学学院苏步青班的无学分讨论班和“莙政基金”大学生见习研修计划等.感谢相关文献对本文的启发以及审稿专家提出的宝贵意见！