参数化结构静态响应特性的减基分析方法
2021-05-07张正
张 正
1.吉首大学信息科学与工程学院,吉首,4160002.吉首大学农矿装备研发中心,吉首,416000
0 引言
工程实践中参数化结构的特性分析[1-2],比如结构响应的灵敏度特性分析[3-4]是一个重要的研究领域。参数化结构的特性分析是建立在参数域与响应集合映射关系之上的,其响应关于参数的灵敏度分析需要计算求解结构响应的有限元向量解。工程中的结构一般较为复杂,离散之后的系统也较为庞大,故而针对结构响应的单次有限元分析耗时较长,尤其对参数域的灵敏度极值这类需要反复多次计算求解结构响应有限元解的问题来说,分析耗时过长,工程上往往难以接受。
结构响应的灵敏度极值分析首先需要分析响应关于参数点的灵敏度计算式,然后在此基础上将其推广至全参数域范围实施遍历,进而获得相应的灵敏度极值模型。减基法(RBM)[5-7]能在线高效计算诸多问题的向量解,它在结构响应分析方面计算效率较高,同时在合适的减基空间中计算精度较高[8-10],故而将减基法直接用于结构响应的灵敏度分析以及灵敏度极值求解等问题具有工程可行性,而这方面的研究工作尚未见诸文献。
本文研究结构参数域与响应集合之间的减基映射特征,建立结构参数点的灵敏度减基计算式,给出了结构的两个灵敏度减基极值模型,并通过结构算例进行验证。
1 减基灵敏度分析
参数化结构静态响应的有限元平衡方程式为
(1)
式中,μ为结构参数的向量形式;Ω为结构的参数域;m为参数域的维度;K(μ)为结构的参数化刚度矩阵;u(μ)为结构参数化的位移响应向量;F为载荷向量。

KN(μ)αN(μ)=FN
(2)
(3)
j=1,2,…,p
式中,KN(μ)为结构的N阶减基刚度矩阵;FN为与参数无关的N阶减基载荷向量;αN(μ)为需求解的N阶权系数向量;σj(μ)为受参数影响的标量函数;Kj为结构分离参数获得的n阶刚度矩阵,p为其刚度矩阵分离数目;BN,j、FN分别为不受参数影响的N阶矩阵和向量。
综合减基空间中的基矩阵ZN,可以得到结构在减基空间中的减基位移响应:
uN(μ)=ZNαN(μ)
(4)
离线处理阶段将式(3)中的BN,j、FN与ZN予以计算并存储;在线处理阶段则依式(3)、式(2)、式(4)的顺序进行调用并计算。
取减基位移响应向量uN(μ)中的一个节点响应作为研究对象,其位移响应记为uN(μ)。在N维减基空间UN中,结构参数向量μ与减基位移响应uN(μ)形成一个连续映射关系:
μuNμ∈Ω
(5)
考虑到结构位移响应随着结构参数的变化而变化,取参数向量μ的分量,即参数分量μi(i=1,2,…,m),研究其对结构位移响应的影响,可以得到减基位移响应uN(μ)关于参数分量μi的变化率为
(6)
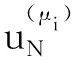
(7)
可以看出,式(7)为减基灵敏度的单步差分形式。由于结构参数向量μ与减基位移响应uN(μ)之间形成的连续映射关系是一个黑箱函数,没有显性的表达式,需要利用减基平衡方程式实施点对点的计算,故而减基灵敏度的单步差分式(7)容易造成结构数值计算的奇异性。为了保证结构数值计算的稳定性,需将单步差分形式转变为两步差分形式,因此参数化结构的减基灵敏度计算式可变为
(8)
2 减基极值模型
对于参数化结构的分析问题,在全参数域范围内求解结构节点响应关于参数分量μi(i=1,2,…,m)的灵敏度极值才具有实际的工程意义。由式(8)推导出在结构参数点μ处,节点响应关于参数分量μi的减基灵敏度计算式,如将其在全参数域范围内遍历搜寻极值,即可快速获得参数分量μi的全域灵敏度极值。这是一个减基的工程优化问题。
全参数域上,节点响应关于参数分量μi的灵敏度极值模型的减基形式可表示如下:
(9)
对于减基的工程优化问题(式(9)),只能快速求解节点响应关于参数分量μi的全域灵敏度极值,而不能同时分析全部参数分量的全域灵敏度极值。在全参数域上,同时分析全部参数分量的灵敏度极值是一个工程上的向量优化问题,即多目标优化问题。
综合式(8)描述的减基灵敏度计算式,节点响应关于全部参数分量的全域灵敏度极值模型的减基形式可表示如下:
(10)
式(10)所示的多目标优化问题没有具体的工程意义上的优化解,只有Pareto最优解[11],即会有一个Pareto前沿以供工程上的参考与决策。式(9)和式(10)所描述的两个工程极值模型由于来源于减基空间下的减基映射关系及其减基列式,因此是两个具有高效计算特征的工程优化问题,并且它们的离线存储与在线调用等处理过程与减基法的计算过程是一致的。
3 结构数值算例
研究图1所示的参数化薄平板结构。l1=0.5 m,l2=0.25 m,厚度为0.02 m,载荷f=380 kN,结构左端为固定端约束。结构的材料参数为弹性模量E(GPa)和泊松比υ,将材料参数记为向量形式μ=(μ1,μ2)T=(E,υ)T∈Ω,其中Ω为结构的参数域(110,220)×(0.15,0.3),它的维度m=2。将结构用有限元离散成为具有n个自由度(n=3048)的系统,取图1中节点O处的竖向位移响应进行观测和研究。在有限元的求解环境下,O点处竖向位移响应关于弹性模量E的灵敏度记为|u(μ1=E)(μ)|,而它关于泊松比υ的灵敏度则记为|u(μ2=υ)(μ)|。该结构算例的数值模拟在MATLAB软件环境下实施,计算机采用i5-7400CPU、8G内存以及64位操作系统。

图1 薄平板结构算例Fig.1 An example of thin plate structure
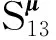
(11)
同样的过程,依据式(9)获得利用减基法分析响应关于泊松比υ的灵敏度极值模型:
(12)
类似的过程,依据式(10)获得同时分析弹性模量E和泊松比υ灵敏度的减基极值模型:
(13)
针对结构算例的灵敏度极值模型(式(11)和式(12)),将数值计算中的有限微元分别选为Δ(μ1)=Δ(E)=1.1×10-3与Δ(μ2)=Δ(υ)=1.5×10-5,并利用遗传算法[13]进行在线计算。设遗传算法的种群数为70,最大寻优代数为60,并使其随机发生器的状态保持一致。
针对式(11)描述的减基极值模型,利用遗传算法搜索响应关于弹性模量E的灵敏度极值为2.748 09×10-5m/GPa,其寻优过程如图2所示。利用遗传算法结合有限元搜索响应关于弹性模量E的灵敏度极值为2.747 49×10-5m/GPa,其寻优过程如图3所示。
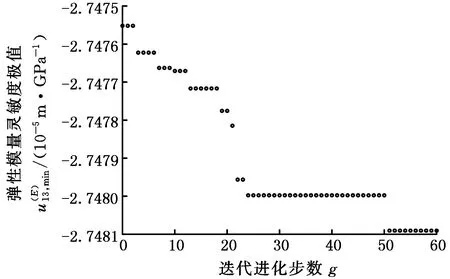
图2 减基法分析响应弹性模量灵敏度极值Fig.2 The sensitivity extremum of elasticity modulusof response by RBM
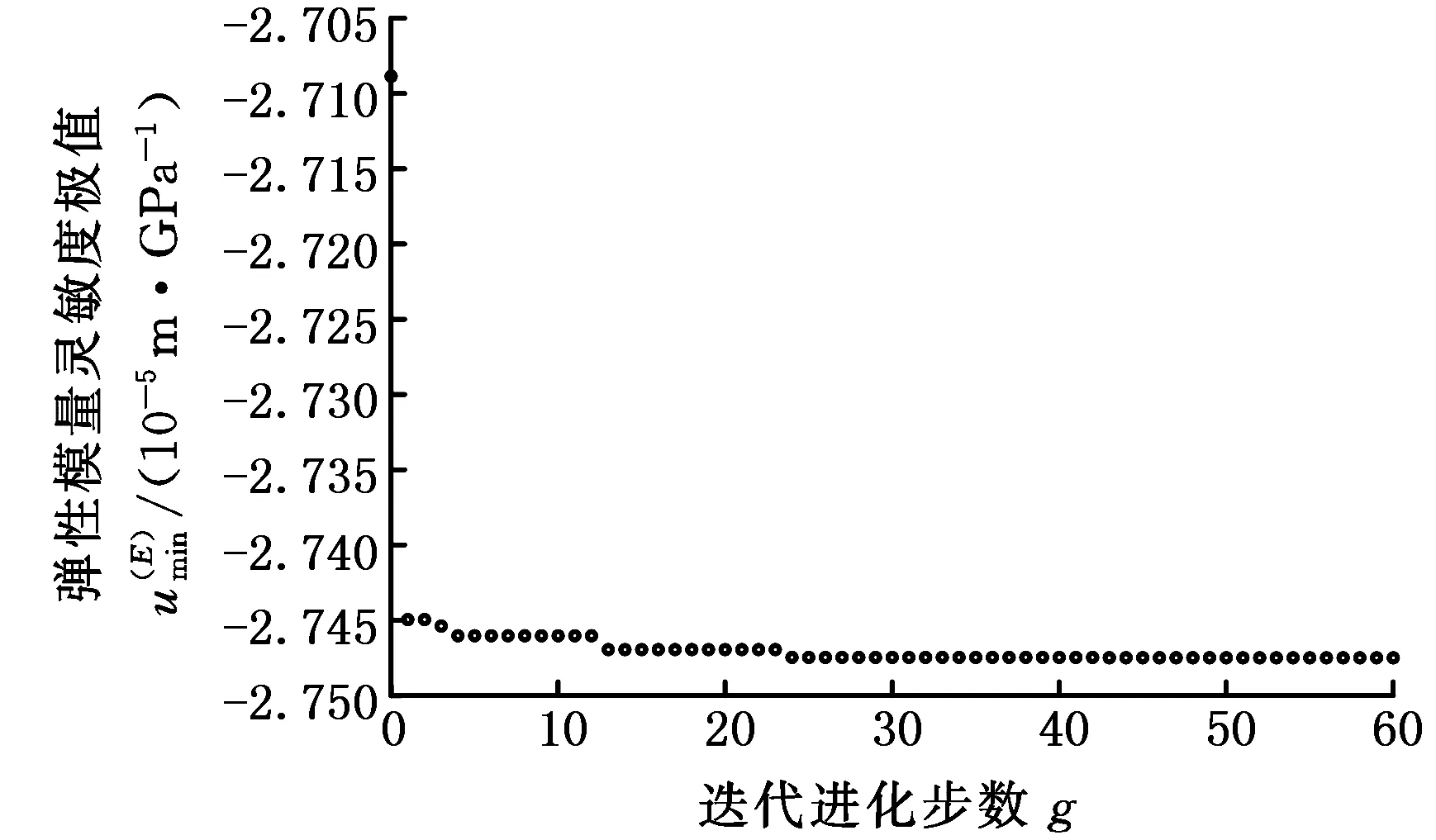
图3 有限元分析响应弹性模量灵敏度极值Fig.3 The sensitivity extremum of elasticity modulusof response by FE
针对式(12)描述的减基极值模型,利用遗传算法搜索响应关于泊松比υ的灵敏度极值为0.311 221 mm,其寻优过程如图4所示。利用遗传算法结合有限元搜索响应关于泊松比υ的灵敏度极值为0.308 565 mm,其寻优过程如图5所示。
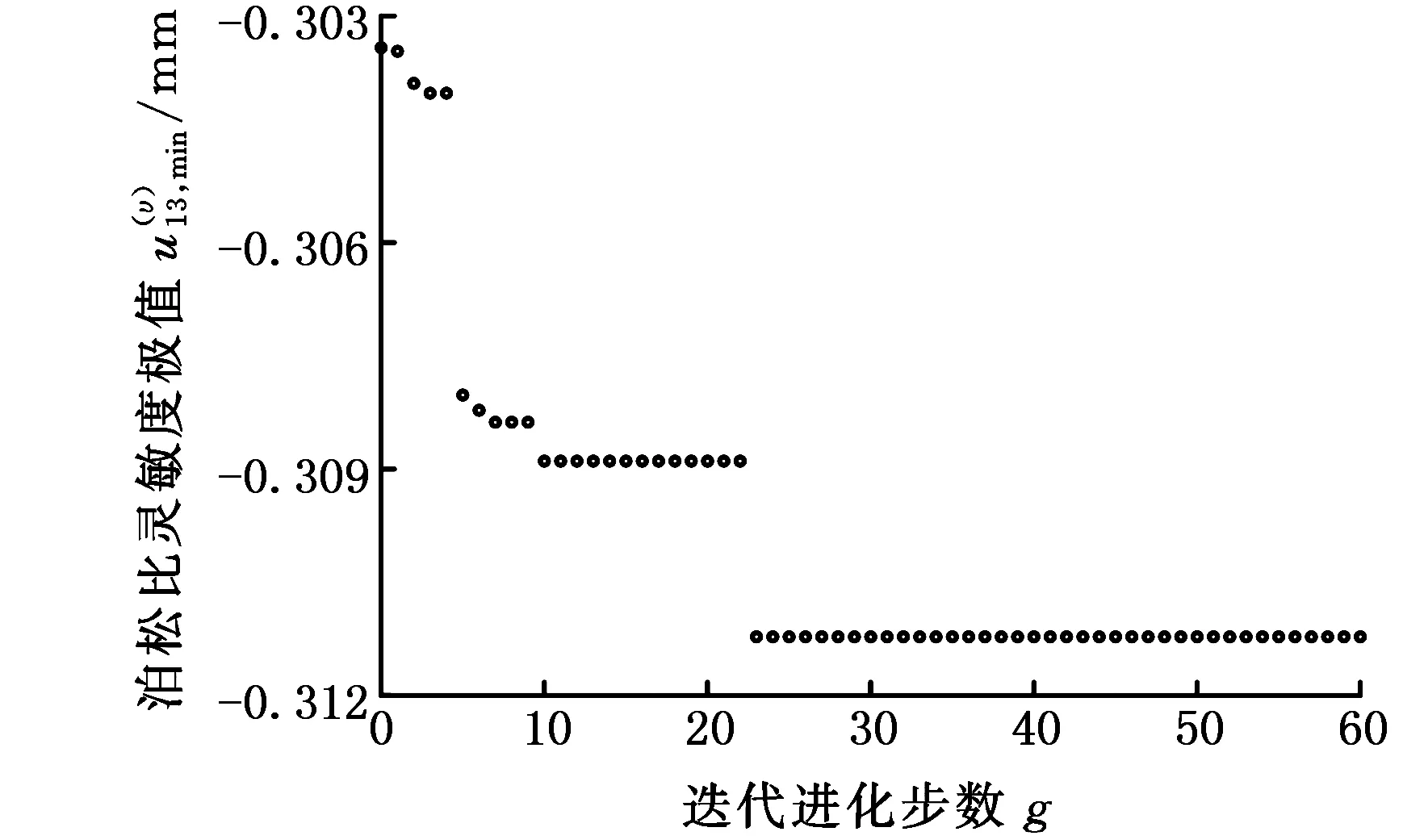
图4 减基法分析响应泊松比灵敏度极值Fig.4 The sensitivity extremum of Poisson’s ratioof response by RBM
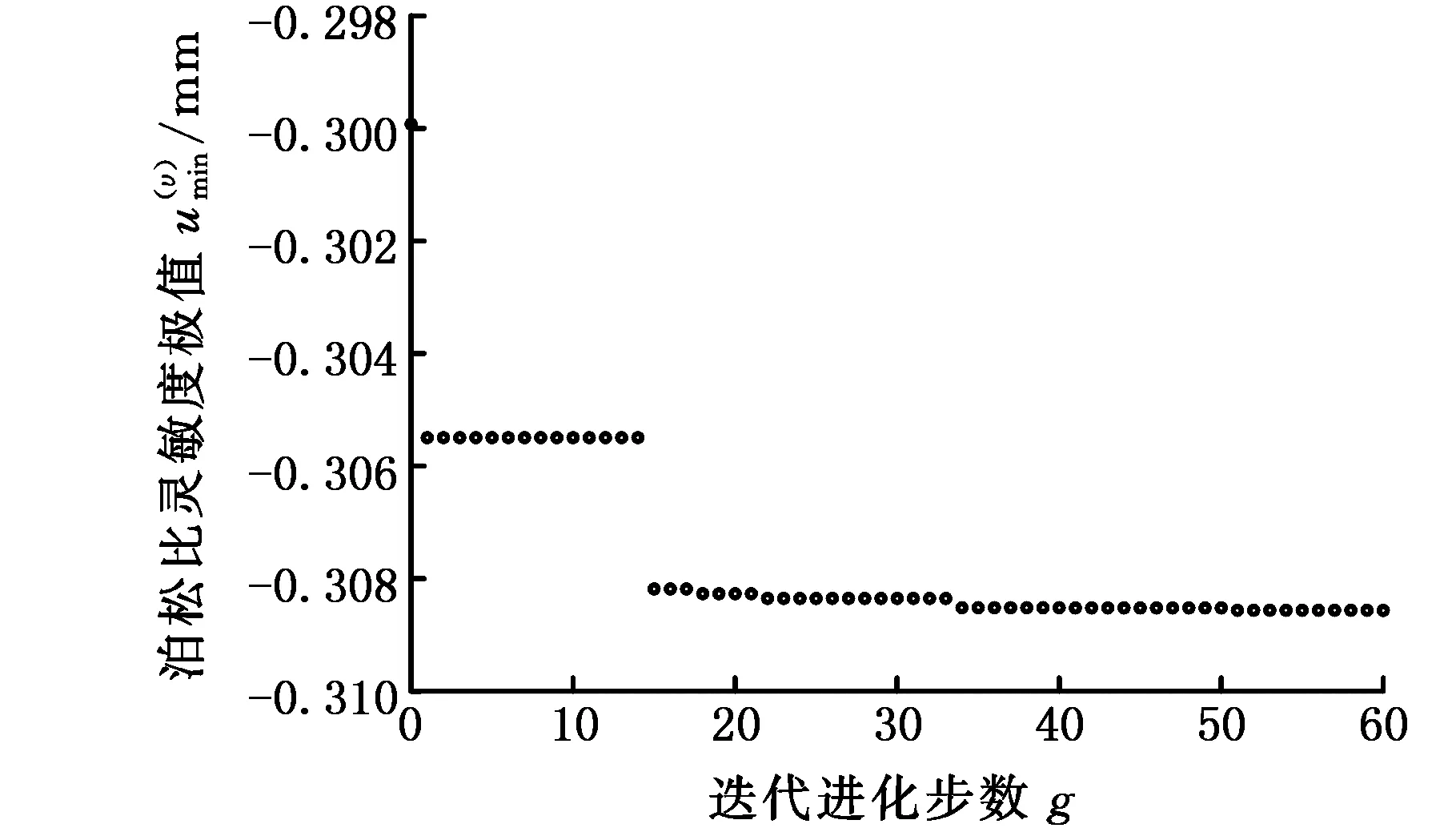
图5 有限元分析响应泊松比灵敏度极值Fig.5 The sensitivity extremum of Poisson’s ratioof response by FE
将有限元解作为标准解,弹性模量E灵敏度极值的减基算法相对误差为2.2×10-4,而泊松比υ灵敏度极值的减基算法相对误差则为8.6×10-3,可以看出,减基法在13维的减基空间中就具有极高的在线计算精确度。另外,同一台计算机上,利用减基法在线求解弹性模量E和泊松比υ灵敏度极值的计算时间皆约为2.5 s,而采用有限元在线求解弹性模量E和泊松比υ灵敏度极值的计算时间皆约为144.5 s,可以看出,减基法具有相对极佳的在线计算时效性。
针对结构算例的全参数灵敏度极值模型(式(13)),利用多目标遗传算法[14]进行在线计算。将遗传算法的种群数量尺寸设置为60,最大寻优代数设置为60,并将其Pareto 前沿的群体比例设置为0.7。针对式(13)描述的减基极值模型,利用遗传算法寻优获得的Pareto 前沿如图6所示。作为比较,利用遗传算法结合有限元极值模型获得的Pareto 前沿如图7所示。由图6与图7所示的搜索结果可以看出,利用减基法所获得的Pareto 前沿与有限元所获得的Pareto 前沿几乎是一致的,其中的细微差别是由减基计算中的数值误差所致。另外,同一台计算机上,遗传算法在线求解减基极值模型所耗费的时间约为3.4 s,而遗传算法在线求解有限元极值模型所花费的时间约为250.5 s,减基法具有相对极佳的计算时效性。
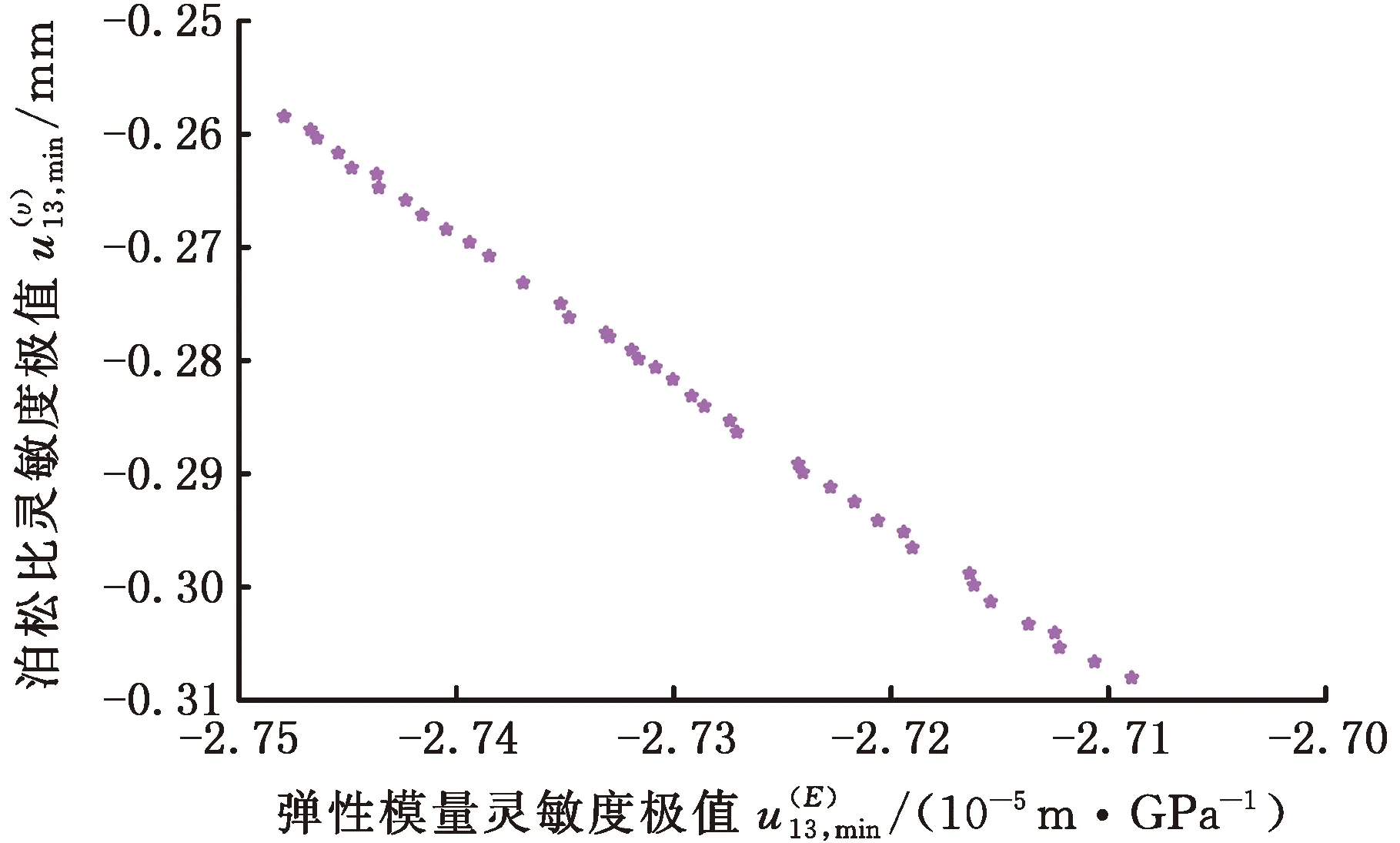
图6 减基法分析结构响应灵敏度极值的Pareto前沿Fig.6 The Pareto front of sensitivity extremum ofstructural response by RBM
4 结语
本文提出了一种快速分析参数化结构静态响应特性的减基方法。对于参数化结构,直接利用减基平衡方程作为映射关系进行响应特性分析,同时通过两步差分法得到了响应关于参数点的灵敏度减基计算式,进而获得了全参数域范围上的灵敏度减基极值模型以及全参数的灵敏度减基极值模型。结构算例的数值计算结果表明,相较于有限元法,该方法能够在确保极高计算精度的条件下获得极佳的计算效率,具有工程上的可行性和有效性。文中所提的方法为一般性的结构灵敏度分析方法,在具体的工程实践中可以推广应用于复杂装备的响应特性分析工作。
