基于混合遗传鲸鱼优化算法的柔性作业车间自动导引车融合调度方法
2021-05-07李西兴杨道明
李西兴 杨道明 李 鑫 吴 锐
1. 湖北工业大学机械工程学院,武汉,430068 2. 湖北工业大学现代制造质量工程湖北省重点试验室,武汉,430068
0 引言
随着我国制造业的改革优化和创新发展,传统的大规模标准化生产模式逐步被大规模个性化定制模式取代。同时,借助于云计算、大数据、数字孪生等“互联网+制造”技术落地生根,大规模也逐渐被小批量替代(尤其是在零部件制造企业)。另外,为了快速应对市场变化,交货期也进一步缩短。多品种、小批量、短周期、个性化的制造特点对企业业务流程(包括加工作业流程、紧急事件处理流程)的优化提出了更高要求,优化制造资源配置策略、提高制造资源利用率成为制造企业亟需解决的问题。传统的制造任务与机器、人员间的优化配置逐步扩展为多类型制造资源间的集成优化,其中作业车间自动导引车(automated guided vehicle,AGV)参与的集成调度逐渐成为生产调度优化领域的重点研究问题之一。
AGV是一种具有高柔性、高效率、高可靠性、智能化的物流运输装备,相关应用和研究主要分布在以下两个领域。
(1)仓储运输领域[1-4]。主要包括:考虑堆场缓冲区大小的自动堆垛机与AGV集成优化调度[5];考虑岸桥、丁升式AGV和自动轨道吊协同调度的混合式自动化码头设备协同调度[6];考虑充电过程的垂岸式集装箱堆场布局和AGV作业集成调度[7]。梁承姬等[8]针对AGV数量偏多导致的自动化码头运输区拥堵问题,采用多学科变量耦合优化设计的方法建立了AGV协调调度与优化配置耦合模型,并利用改进遗传算法(genetic algorithm,GA)进行求解,但未考虑场桥对AGV的影响。
(2)作业车间领域[9-11]。XU等[12]针对智能制造车间的物流动态调度问题,提出了一种基于“需求-调度-反馈”模式的AGV智能物流调度模型和响应方法,同时应用物联网技术以满足动态和实时性的需求。CHEN等[13]提出了一种基于AGV的模块化预制制造系统的设施布局规划方法,以最小化生产时间和最大化工作站利用率为优化目标。魏永来等[14]将整车间物料调度视为一个小型车间物料系统,提出了以AGV路径-运输时间-配送成本为目标的多AGV调度优化模型,将禁忌搜索算法引入蝙蝠算法并求解,通过某实际车间进行了仿真验证。FONTES等[15]将联合生产运输调度问题转化为一种新的混合整数线性规划模型,即集成机器调度问题和AGV调度问题,构建了两组链式决策策略(一组用于机器,另一组用于AGV),通过机器操作和运输任务的完成时间约束相互连接。刘二辉等[16]综合考虑AGV的利用率和工件最大完工时间两个因素建立了面向共融AGV作业车间的多目标优化数学模型,利用改进花授粉算法求解并搭建集成调度平台进行验证。贺长征等[17]为了实现AGV路径规划与机器调度的同步集成,搭建了AGV/机器的双资源调度数学模型,同时针对路径冲突问题制定了速度调节、几何路径调节和混合调节的解决策略,增强了模型的动态优化能力,但忽略了小车充电和故障问题。在实际作业车间中,AGV的物理属性(如规格型号、功率、运载能力、续航时间等)存在差异,不同行走路径带来的时间消耗不同,会对整个工件任务的加工时间、调度规划、完工交货造成影响。为了增强调度方案的可行性和合理性、保障生产任务的顺利执行,作业车间AGV融合调度研究具有重要意义。
AGV参与的集成调度问题有多种求解方法[18]。CHEN等[19]针对制造空间受限且有AGV参与的家具制造车间,提出了基于规则的染色体评估方法对传统GA进行改进,进而提高其求解性能。而DANG等[20]建立了面向AGV调度的整数规划模型,将禁忌搜索算法与GA混合来求解最大完工时间最小化问题。LYU等[21]同时考虑了最佳AGV数量、最短运输时间、路径规划问题和无冲突路由问题,提出了一种基于时间窗的GA与Dijkstra算法相结合的混合求解算法。岳笑含等[22]考虑AGV电量状况,以最小完成时间与调度最少AGV数量作为优化目标,提出了一种改进的混合GA-粒子群优化(particle swarm optimization,PSO)算法对问题进行求解。范佳静等[23]提出了改进分散搜索算法,将其应用于以AGV数量最少为目标的多目标规划模型,即通过GA获得新解,利用模式搜索法改进新解,从而提高算法收敛速度。LI等[24]提出了一种改进的和声搜索算法对以AGV缓冲区等待时间和总行驶距离为目标的优化数学模型进行求解。
综上所述,目前对AGV参与的集成调度问题,尤其是将其与FJSP相结合的研究较少;同时,在探索优化求解算法方面大多还是以GA、PSO等传统元启发法式算法为主,因此,本文针对柔性作业车间AGV融合调度问题,提出使用混合遗传鲸鱼优化算法(hybrid genetic whale optimization algorithm,HGWOA)进行求解。该方法综合考虑AGV与FJSP问题的集成优化,引入遗传算法中的交叉/变异算子来保证WOA可行解的多样性,通过3种邻域结构和精英池策略来提高算法的局部寻优能力。最后通过实例验证了该方法的有效性和可行性。
1 问题描述
柔性作业车间调度问题可描述为:n个工件在m台机器上加工,每个工件均有多道具有顺序约束的工序,每道工序均具有一台或者多台可选加工机器,通过合理安排工序加工顺序和加工机器以使给定指标最优化。
本文在柔性作业车间调度问题基础上加入AGV资源约束,考虑AGV在装载站/卸载站、机器输入输出缓冲区之间运输工件,各段距离及AGV运行速度已知,相邻设备间距不等。工件从装载站开始,依次被运输到安排的设备输入区,工序加工完成后放入输出区,由AGV将其运输至下一台设备,加工完成的工件送至卸载站。设备单次充电后的运输距离一定,每次运输后距离累计,剩余运输距离不足则AGV不分配运输任务,达到阈值后充电,充电时间一定,充电期间AGV不可用。
1.1 变量定义
表1所示为所有索引及集合变量的定义,表2所示为所有参数变量的定义,表3所示为所有决策变量的定义。

表1 索引及集合含义Tab.1 Index and collection meaning
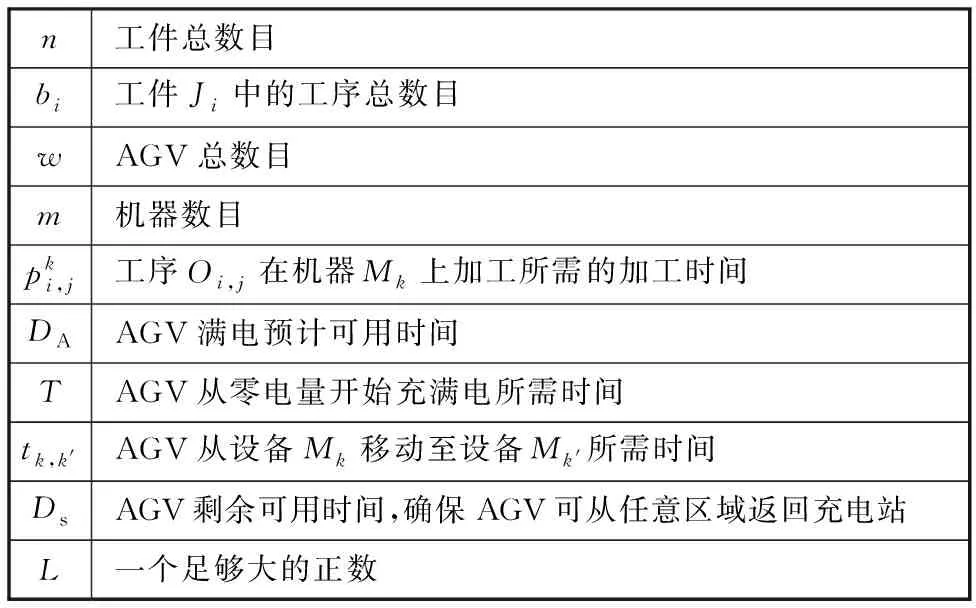
表2 参数及含义Tab.2 Parameters and meaning
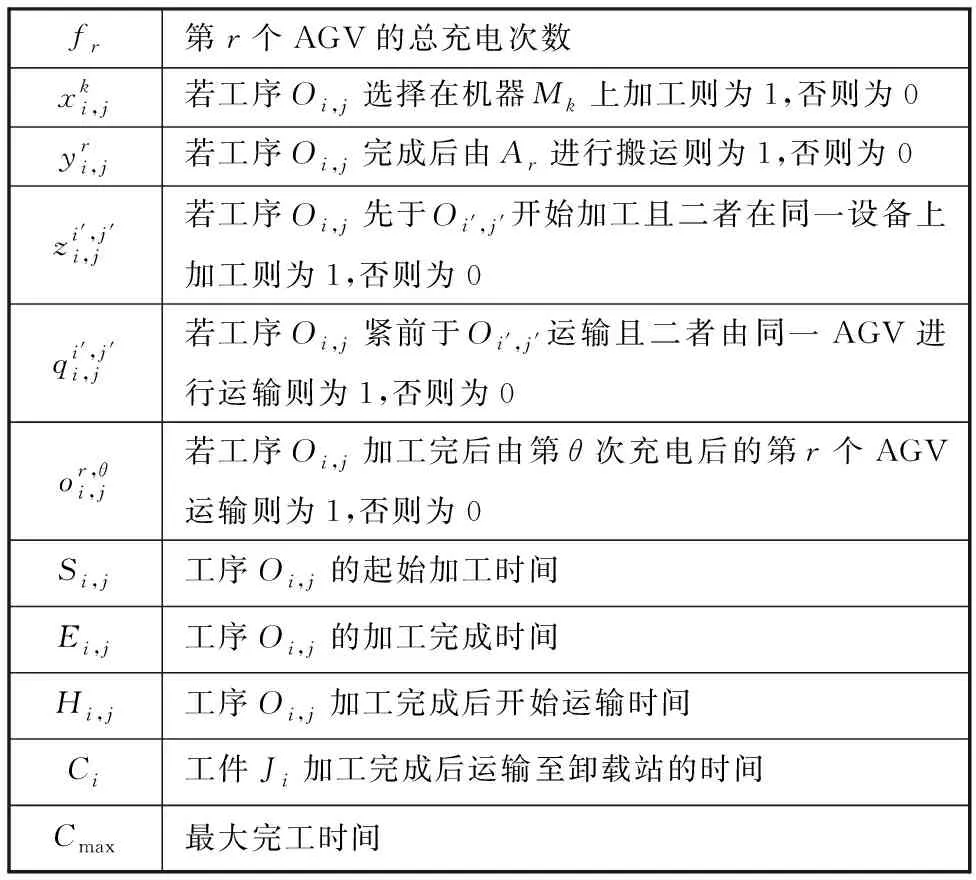
表3 决策变量及含义Tab.3 Decision variables and meaning
1.2 问题假设
(1)不考虑AGV差异性,即运输速度、单次充电运输距离、充电时间等相同。
(2)装载站、卸载站、机器缓冲区容量无限。
(3)不考虑工序开始加工前的准备时间和完成后的释放时间。
(4)工序开始加工和运输后不可中断。
(5)0时刻所有的工件均可被加工,所有机器和AGV均处于可用状态。
1.3 模型建立
优化目标选择车间调度问题中最常使用的是最小化最大完工时间,本文中最大完工时间即所有工件被运输至卸载站所需时间的最大值:
(1)
(2)
i=1,2,…,n
式(2)表示工件运输完成时间等于最后一道工序的开始运输时间加上其运输到卸载站所需时间。
开始运输时间必须晚于其工序加工完成时间,即
Hi,j≥Ei,ji=1,2,…,nj=1,2,…,bi
(3)
工序的加工完成时间等于其起始加工时间加上实际加工所需时间,即
(4)
i=1,2,…,nj=1,2,…,bi
工序约束,即工序的起始加工时间必须晚于其前置工序完成后运输至当前机器的时间,即
(5)
i=1,2,…,nj=1,2,…,bi-1
设备约束如下:
(6)
i,i′=1,2,…,nj=1,2,…,bij′=1,2,…,bi′
式(6)确保一台设备在任一时刻只能加工至多一道工序。
AGV时间约束如下:
(7)
i,i′=1,2,…,nj=1,2,…,bi-1j′=1,2,…,bi′
式(7)表明工序Oi′,j′的起始运输时间必须晚于与其使用同一AGV进行运输的紧前工序完成运输后空载运行至Oi′,j′机器的时间,确保任一台AGV在任一时刻都只执行一个运输任务。
限定一道工序只能选择一台而且必须选择一台可行机器进行加工,即
(8)
限定工序完成加工后必须选择一台且只能选择一台AGV执行运输任务,即
(9)
限定AGV在单次充满电后的运输时间不超出可用的最大运输时间,即
(10)
r=1,2,…,wθ=0,1,2,…,fr
限定AGV在充电之前的最后一道运输任务完成时间加上充满电的时间早于充电后第一道运输任务的起始运输时间,即
(11)
r=1,2,…,wθ=0,1,2,…,fr-1
2 改进鲸鱼优化算法
2.1 鲸鱼优化算法简介
根据座头鲸群体狩猎行为特点——Bubble-net觅食(即泡泡网觅食或气幕觅食),WOA算法抽象出包围猎物、 Bubble-net攻击和随机搜索3个计算阶段。
2.1.1包围猎物
每只鲸鱼代表一个个体,每个个体在搜索空间的位置代表一个解。鲸鱼能够通过回声定位识别猎物位置并包围猎物,鲸鱼位置更新公式如下:
(12)
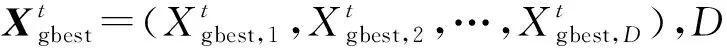
A=2a×rand1-a
(13)
C=2rand2
(14)
其中,rand1、rand2为[0,1]范围内均匀分布产生的随机数;a中元素a为收敛因子,随迭代次数t从2线性减小到0,即
a=2-2t/tmax
(15)
式中,tmax为最大迭代次数。
2.1.2Bubble-net攻击
鲸鱼在觅食过程中是以向上螺旋式运动并不断收缩包围圈来攻击猎物的,为了从数学上描述Bubble-net觅食行为,设计收缩包围机制和螺旋更新位置两种方法。
收缩包围机制通过式(2)随着收敛因子a的减小实现,同时系数向量A的波动范围也随着收敛因子a减小,即当收敛因子a在迭代过程中从2减小到0时,系数向量A的波动范围为[-a,a]。当系数向量A为[-1,1]内的随机值时,鲸鱼t+ 1时刻的位置可以是t时刻的位置与t时刻全局最优位置之间的任意位置,即表示鲸鱼始终在收缩包围圈内游动。
在螺旋更新位置方法中,鲸鱼以螺旋运动向猎物游动,其数学模型为
(16)
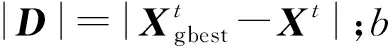
鲸鱼在猎物收缩包围圈内同步沿着螺旋形路径游动,为了模拟这种同步行为,在优化过程中假设选择收缩包围机制和螺旋更新位置概率均为0.5,同步行为的数学模型为
(17)
其中,pr为[0,1]范围内均匀分布产生的随机数。
2.1.3随机搜索
当系数向量|A|> 1时,表示鲸鱼在收缩包围圈外游动,此时鲸鱼个体根据彼此位置进行随机搜索,其数学模型为
(18)

由上述分析可知,WOA算法主要参数为系数向量A和C,其中参数A对协调WOA算法全局探索和局部开发能力至关重要。当|A|> 1时,鲸鱼种群将扩大搜索范围,以找到更好的候选解,即为WOA算法的全局探索能力;当|A|≤ 1时,鲸鱼种群将缩小搜索范围,在局部区域进行精细搜索,即为WOA算法的局部开发能力。而参数A的值在很大程度上依赖于收敛因子a的变化:较大的收敛因子a具有较好的全局搜索能力,避免算法陷入局部最优;较小的收敛因子a具有较强的局部搜索能力,以加快算法的收敛速度。
2.2 编码/解码
根据该问题的特性,采取双层编码方式,即编码后的个体向量由两部分组成:工序排序向量(operation sequence vector,OV)和机器选择向量(machine select vector,MV)。在OV中,各元素表示的是工件的索引号,该索引号第几次出现表明是该工件的第几道工序。MV由各对应工序所选择的机器索引号构成,对应的工序按工件号及工序号由小到大排序。图1中给出了一个3工件5设备问题案例可行解的编码方案。
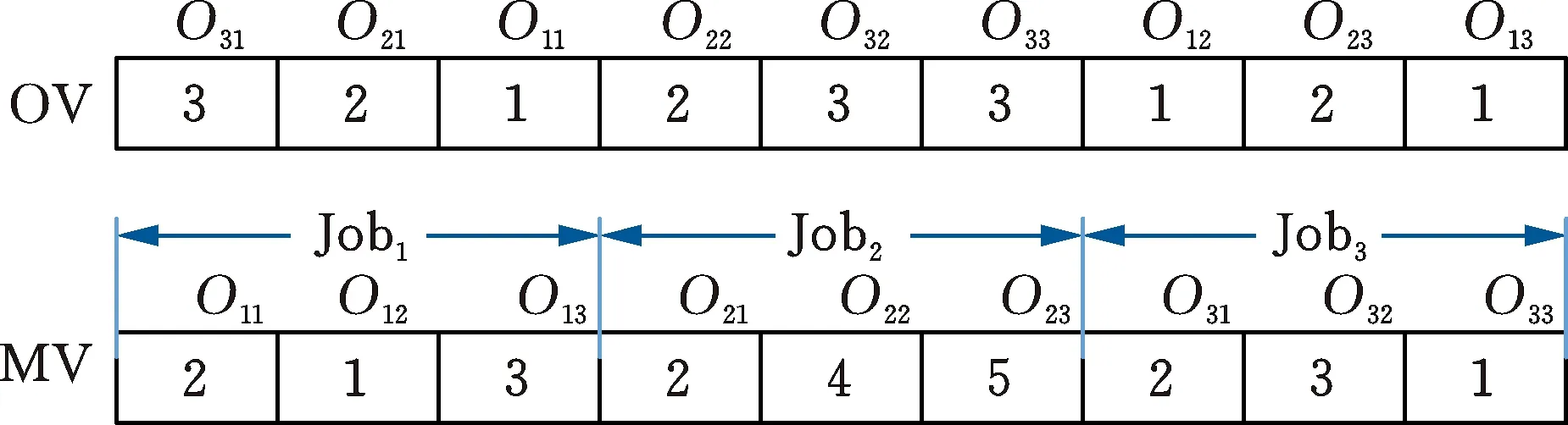
图1 编码方案Fig.1 Coding scheme
上述编码只表述了柔性作业车间调度问题对应的工序排序和设备选择两个子问题,并未包含AGV的选择子问题,因此在解码过程设计中,必须考虑AGV的选择问题。本文基于最先开始服务AGV优先选择的规则设计了以下新的解码算法。
(1)初始化机器可用时间向量αj,工件加工时间向量βi,AGV位置记录向量λr,AGV时间记录向量θr,目标函数值f=0,t=1。
(2)在OV中从左至右取出第t个元素,获得其工件号i和工序号j,并且在MV中取出对应工序的机器序号k,取得对应的加工时间p。
(3)比较βi与αj,将其中的较大值设置为当前工序Oi,j最早开始加工时间Si,j。若j=1,即当前工序为该工件内的第一道工序,则转步骤(4),否则转步骤(5)。
(4)从AGV中选择最早能从当前位置空载运行至装载站的Ar,为Ar添加两个运输任务。一个是从当前位置λr空载至装载站的任务,起始时间为θr,运输时间可通过当前位置至装载站的距离确定,之后计算得到任务终止时间,更新θr为任务终止时间。之后为Ar添加从装载站运输至机器k的运输任务,过程类似。在添加运输任务之后累计Ar的累计运输时长,若剩余时长小于安全值,则为Ar增加充电任务,更新θr为θr、T以及运行至充电站所需时间之和。
(5)获取工序Oi,j的前置工序所在机器k′,然后从AGV中选择最早能从当前位置空载运行至装载站的Ar,若Ar已经在机器k′处,则转步骤(7),否则转步骤(6)。
(6)为Ar添加一个从AGV当前所在设备位置空载至前置工序所在机器k′的任务,起始时间为θr或前置工序的加工完成时间中的较大值,计算得到任务完成时间,更新θr为任务完成时间。
(7)为Ar添加从机器k′运输工件至机器k的运输任务,起始时间为θr,计算得到任务完成时间,更新θr为任务完成时间。同样更新和判断Ar累计运输时长,若剩余时长低于安全值则添加充电任务。
(8)更新工序Oi,j的起始加工时间Si,j,设置其为步骤(3)中Si,j与步骤(4)或步骤(7)中运输任务完成时间中的较大值,工序Oi,j完成时间则为Si,j+P。若Si,j+P大于f,则设置f为Si,j+P。
(9)若t小于编码长度,t←t+1,则转步骤(2),否则终止。
2.3 种群初始化
初始解质量的好坏会直接影响算法的求解性能,完全随机生成虽然使初始种群具有良好的多样性,但是具有一定的盲目性。为了提高算法初始解的质量并保持良好的多样性,本文采用了混合初始化策略来生成初始解,混合初始化策略包含随机初始化方法和策略选择初始化方法。根据文献[35-36],本文种群中30%的个体采用随机初始化方法生成,即工件随机排序,工序对应的机器在合法范围内随机选择;剩余70%的个体采用策略选择的方法生成,将工件随机排序,在选择合法机器时考虑加工时间的因素,选择最可能加工时间小的机器对工件加工。
2.4 改进搜索策略
在改进搜索操作中,引入遗传算法中的交叉/变异算子来保证可行解的多样性;提出3种邻域结构和精英池策略来提高算法的局部寻优能力。
2.4.1交叉变异算子
针对OV、MV向量各自的特点分别设计了高效的交叉和变异操作,以实现搜索操作,即在鲸鱼优化算法的包围猎物、 Bubble-net攻击搜索中使用交叉算子,随机搜索操作中使用变异算子。
(1)OV的交叉操作采用广泛使用的POX交叉方法[37],操作过程如下:①将工件序号随机分配到两个非空且互补的集合Q1和Q2中;②从父代X1选出包含在集合Q1中的工件序号,保持各工件序号的位置不变复制到子代X′中;③从父代X2中选出包含在集合Q2中的工件序号,将其按顺序依次插入子代X′的空缺处;④按照步骤②和③的操作,从父代X1中选出包含在集合Q2中的工件序号,保持位置不变复制到子代X″中,从父代X2中选出包含在集合Q1中的工件序号,按顺序插入子代X″的空缺处;⑤从子代X′和X″中选出较优的个体作为交叉后的子代。
(2)MV的交叉操作采用RPX(radom probability crossover)交叉操作,即遍历MV中的元素,以50%的概率交换两个体MV中元素。
(3)OV的变异操作采用常用的两点交叉操作。
(4)MV的变异采用替换变异,即随机选择MV中的一个元素将其替换为可用机器集合内的另外一台机器。
2.4.2 3种邻域结构和精英池策略
本文提出3种邻域结构:①交换邻域结构,将个体的OV向量任意指定的两个位置进行交换得到新的个体;②插入邻域结构,指定个体的OV向量的某一元素插入到该OV向量的任意指定位置;③变异邻域结构,以一定的概率对MV中的元素进行合法替换变异。基于上述3种邻域结构,引入一种基于精英池的迭代局部搜索进行局部搜索操作。具体操作流程如下:
(1)将全局最优个体作为迭代搜索的初始解π,设置tcn=0。初始化精英池中只有初始解π。
(2)利用交换邻域结构对π进行搜索操作,得到新解π′。若π′优于π,则设置π=π′,tcn=0,将π′插入精英池中,转至步骤(5);否则设置tcn←tcn+1,转至步骤(3)。
(3)利用插入邻域结构对π进行搜索操作,得到新解π′。若π′优于π,则设置π=π′,tcn=0,将π′插入精英池中,转至步骤(5);否则设置tcn←tcn+1,转至步骤(4)。
(4)利用轮盘赌方法从精英池中选择最优个体,并对其使用变异邻域结构进行搜索得到新解π′,若π′优于π,则设置π=π′,tcn=0,将π′插入精英池中,转至步骤(5);否则设置tcn←tcn+1,转至步骤(5)。
(5)若tcn<5,则跳转至步骤(2),否则终止。
2.5 HGWOA算法基本流程
综上所述,HGWOA算法步骤总流程如图2所示,具体描述如下:
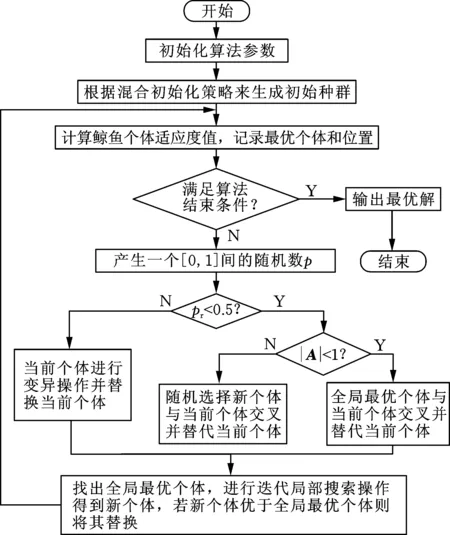
图2 HGWOA算法流程图Fig.2 HGWOA algorithm flow chart
(1)初始化算法参数。
(2)根据初始化策略初始化鲸鱼种群,对种群进行评价,找出全局最优个体。
(3)迭代开始,依次遍历种群中的个体。生成一个[0,1]之间的随机数pr,若pr<0.5,则转步骤(4),否则转步骤(5)。
(4)若|A|<1,则随机选择一个不同于当前个体的新个体,基于当前个体与新个体进行交叉操作,获得一个新个体替换当前个体。若|A|≥1,则选择全局最优个体与当前个体进行交叉操作。
(5)基于当前个体进行变异操作,利用变异后的个体替换当前个体。
(6)对种群进行评价,找出全局最优个体,基于全局最优个体进行迭代局部搜索操作,评价搜索得到的个体,若优于全局最优个体则替换。
(7)重复上述步骤直到算法达到终止条件,输出结果。
3 仿真对比试验
为验证HGWOA求解所提问题的性能,进行如下操作:首先通过扩展FJSP的经典测试算例得到适用于验证此问题的算例;然后采用正交试验法对HGWOA中的参数进行优化配置;最后,将FJSP中常用的经典算法GA[37]、PSO[38]及差分进化算法(differential evolution, DE)[39]作为对比算法来验证HGWOA的求解性能。选取的3种对比算法经过对应文献中的离散化改进后已适用于求解FJSP,但要适用于求解本文所提出的问题仍需作一定调整,在保证对比算法整体流程不变的基础上,所作调整主要包括改为使用本文提出的编码/解码方案以及对搜索操作进行适应性改进。
3.1 测试算例生成

图3 车间机器布局Fig.3 Workshop machine layout
本文将柔性作业车间调度问题中的经典Brandimarte测试算例[40]进行拓展,附加AGV等相关数据,用于测试本文提出的算法。每个测试算例分别考虑AGV数量与机器数量的比例为1∶1、1∶2、1∶3,以MK01为例,AGV数量与机器数量比例为1∶1时,命名为MK01_1,比例为1∶2和1∶3时分别命名为MK01_2和MK01_3,其余的测试算例类似。假定机器布局如图3所示,X、Y为建立坐标系的X轴、Y轴。装卸载站、充电站以及各机器之间的运输时间可通过图中所示各坐标之间的距离计算得到。此外,AGV满电运行时间DA=30,充满电时间T=20,安全剩余可用时间Ds为各设备至充电站运输时间中的最大值。
3.2 参数配置
相比于其他群智能优化算法,WOA算法具有参数少、使用便捷的特点,需要设置的参数仅有种群规模P。本文采用正交试验法对参数进行优化配置,设置P参数水平分别为20、40、60、80、100共5个水平。基于中等规模的算例MK09进行试验,算法运行30次,取均值作为最终结果值。最终算法运行试验结果分别为640.37、632.37、628.6、640.43、634.63,从中可以得出P=60时HGWOA具有最优的性能。其余对比算法的参数设置与文献中一致。
3.3 算法对比分析
算法采用C#语言进行编写,运行环境为 Intel Core I7-5700HQ CPU 2.70 GHz,RAM 8 GB, Windows 10, 64 位操作系统。为公平对比各算法,所有算法运行时的终止条件设置为固定的最大运行时间,其值等于各算例的工件数目。为避免试验结果的随机性,针对每个算例将算法重复运行30次,得到30个结果值,最终结果取其平均值。试验结果如表4 所示,其中均值指30次运行得到的均值,最优值指30次运行中的最优值,tcpu表示程序运行时间。
从表4中各算例结果的最优值和平均值可以看出, HGWOA在大部分算例上都表现得最为优异,GA次之,HGWOA取得最优的比例远远大于其他对比算法,由此表明HGWOA在求解本文提出的问题时具有更优良的性能。
为了验证算法性能是否确实存在统计意义上的差异,利用试验结果中的数据进行Wilcoxon测试(置信水平为0.05),试验结果如表5所示。表5中p值均小于0.05,说明HGWOA在最优值和均值两指标上均显著好于其他对比算法。
图4为各算法在算例MK01_1、MK05_1、MK09_1、MK15_1进行的30次求解中所获得结果的箱型图。从图中可看出,HGMOA在4个算例中均取得了最小的均值,但是其上限值和下限值并非在4个算例上均取得最优,同时在部分算例上的散布大小并非最小,说明所提出的HGWOA虽然在寻求最优上相比其他算法具有一定优势,但是在算法稳定性上优势并不突出。
图5为HGWOA和对比算法在测试算例MK01_1、MK05_1、MK09_1、MK15_1进行的30次求解中取得最优值的一次运行的收敛曲线图。

表4 试验结果Tab.4 Experimental result
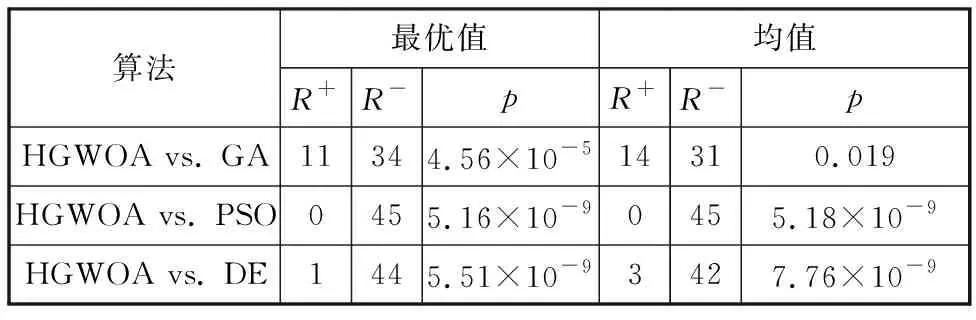
表5 Wilcoxon测试结果Tab.5 Wilcoxon test results
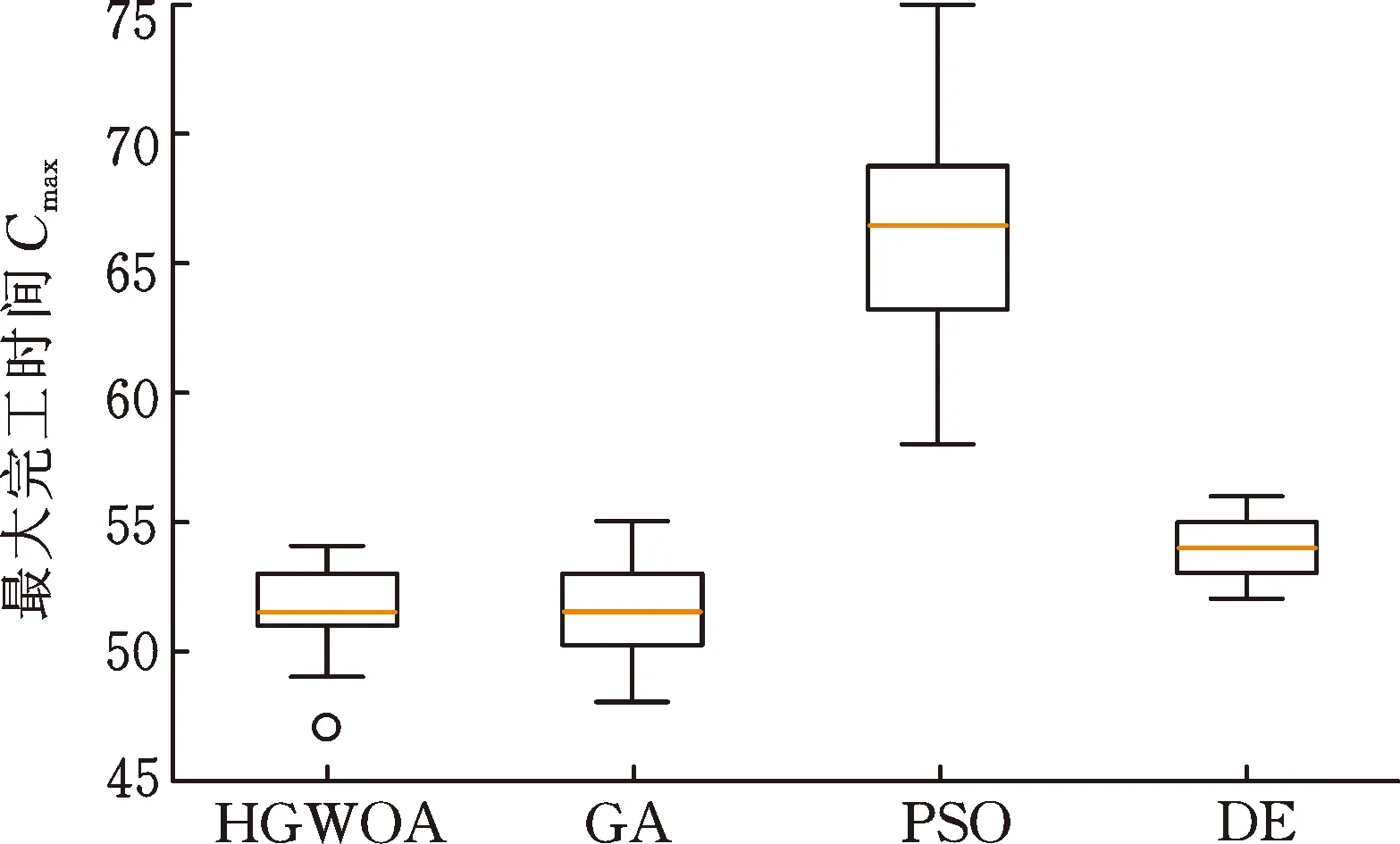
(a) MK01_1
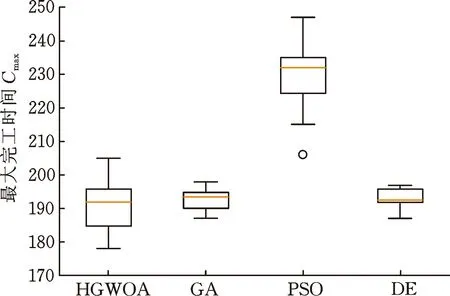
(b) MK05_1
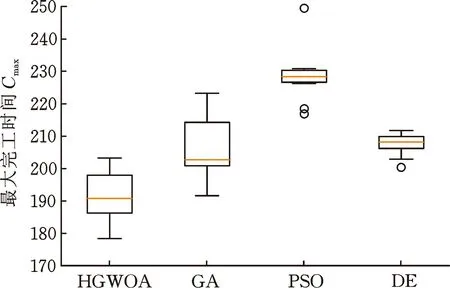
(c) MK09_1
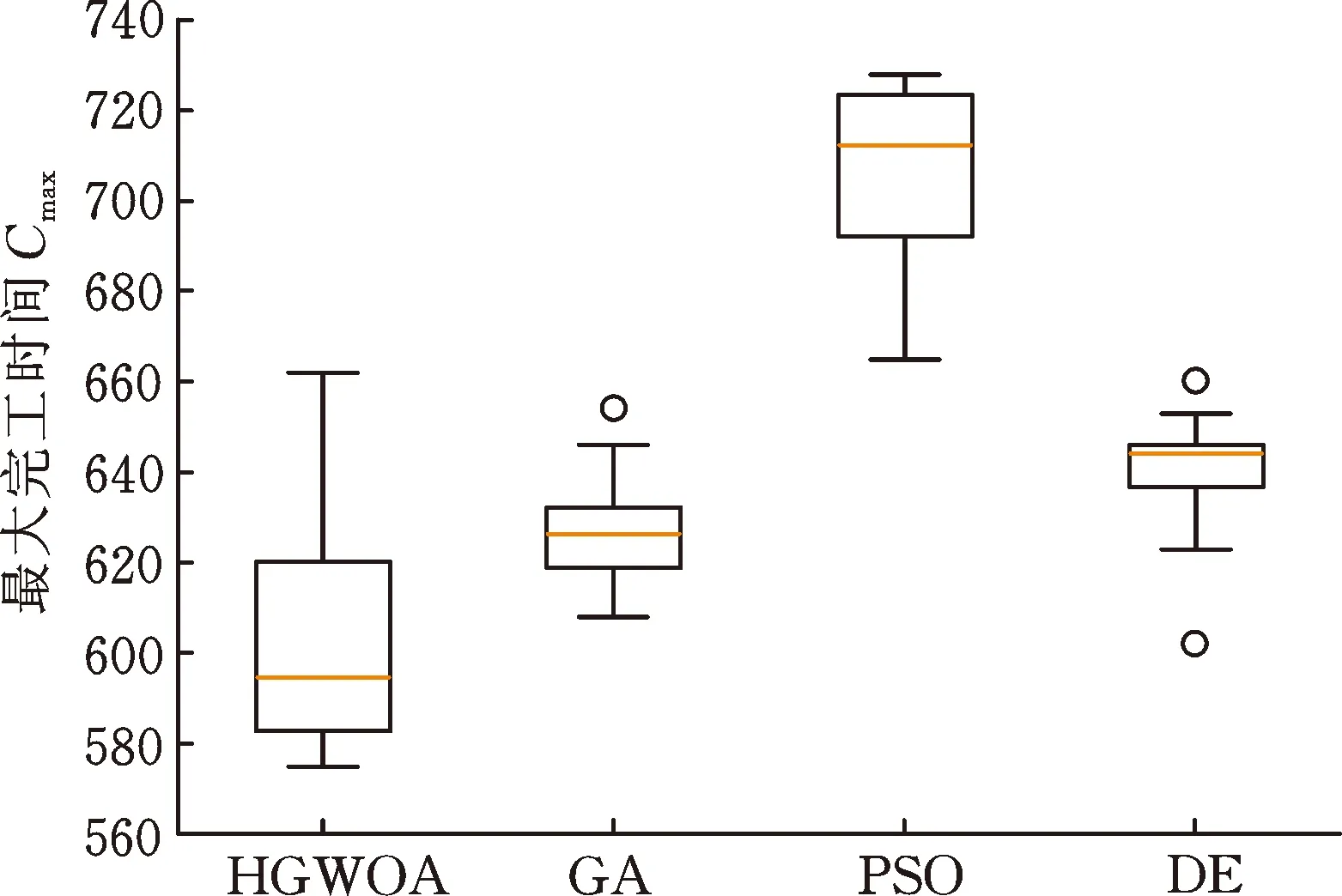
(d) MK15_1图4 30次求解结果箱型图Fig.4 Box plot of 30-time solution results
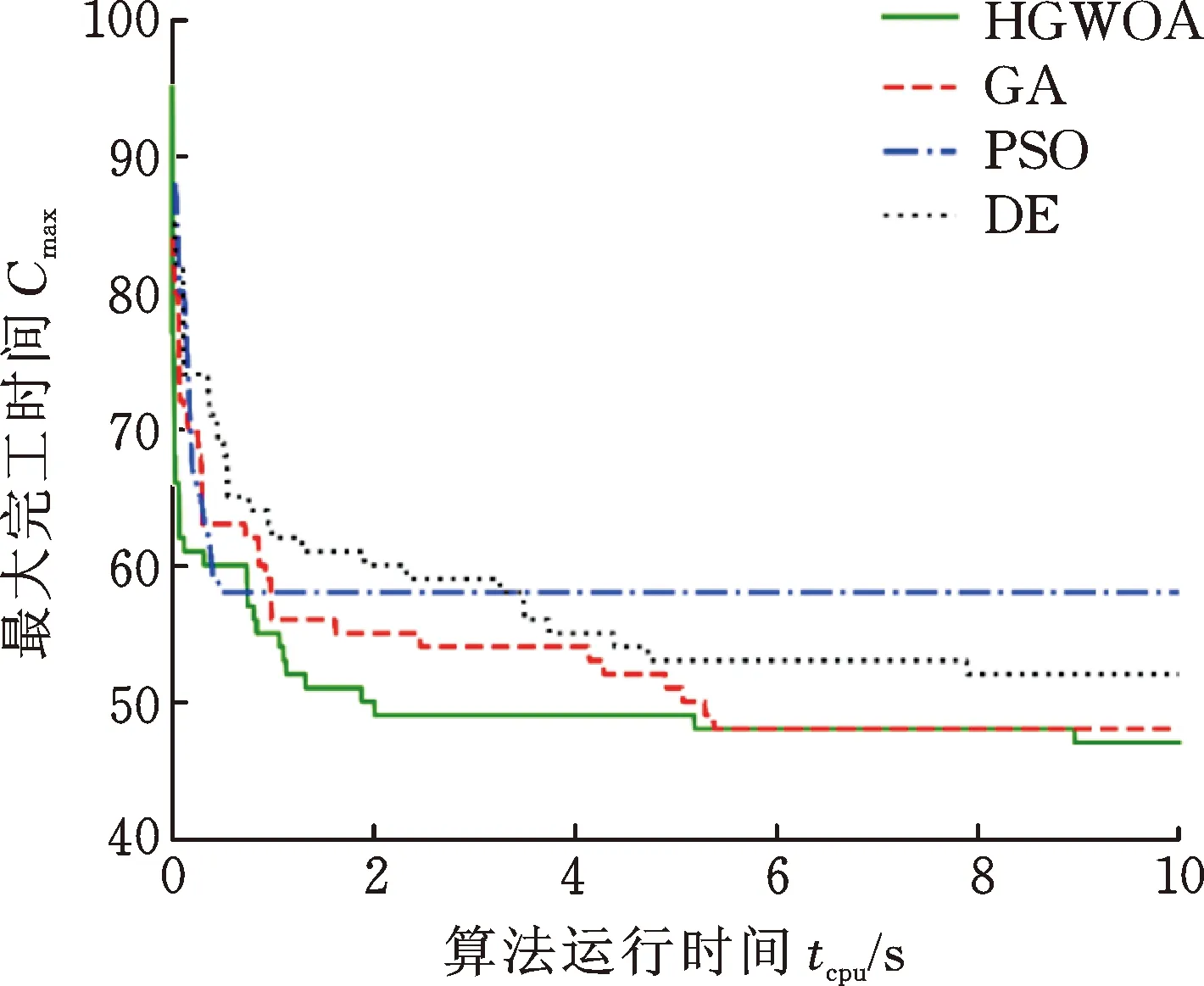
(a) MK01_1
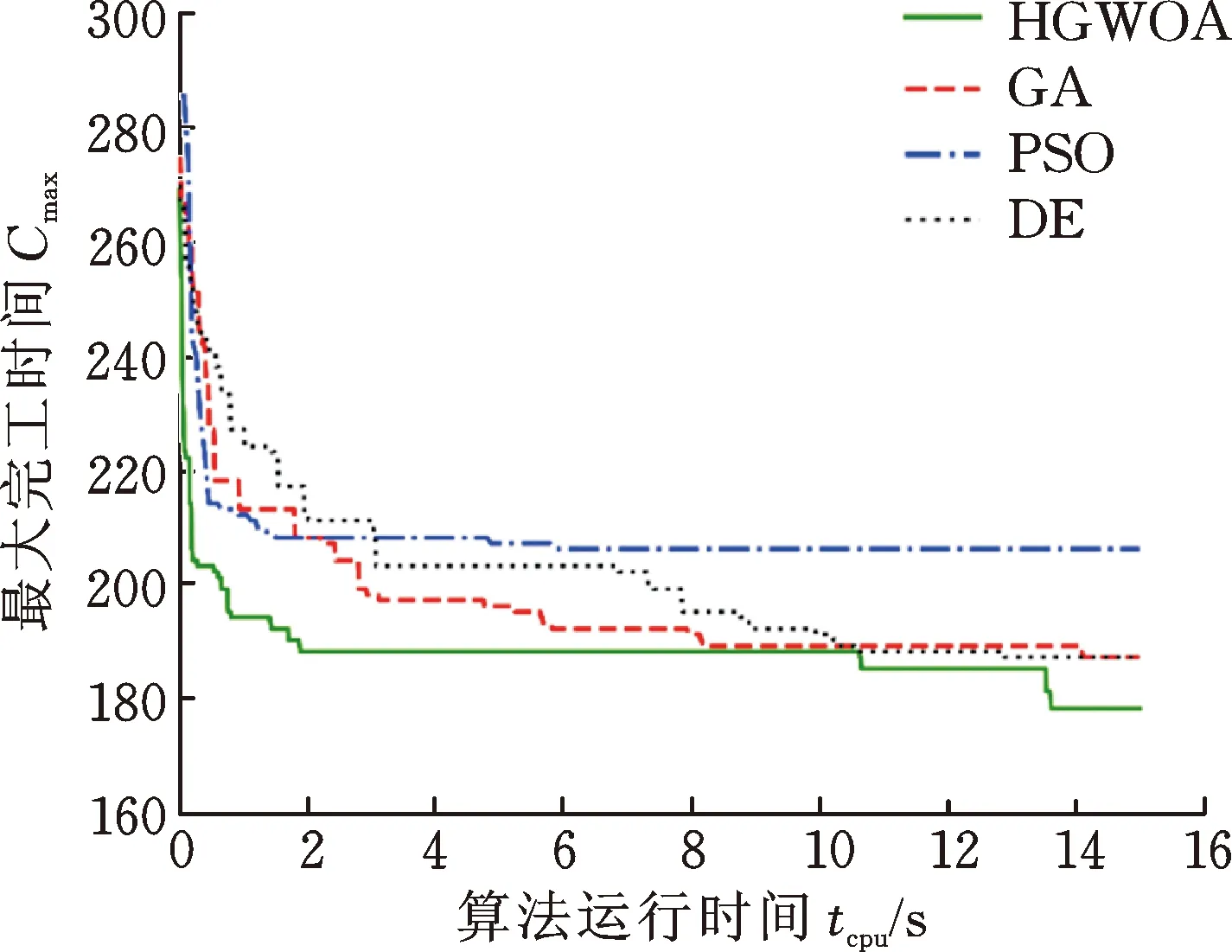
(b) MK05_1
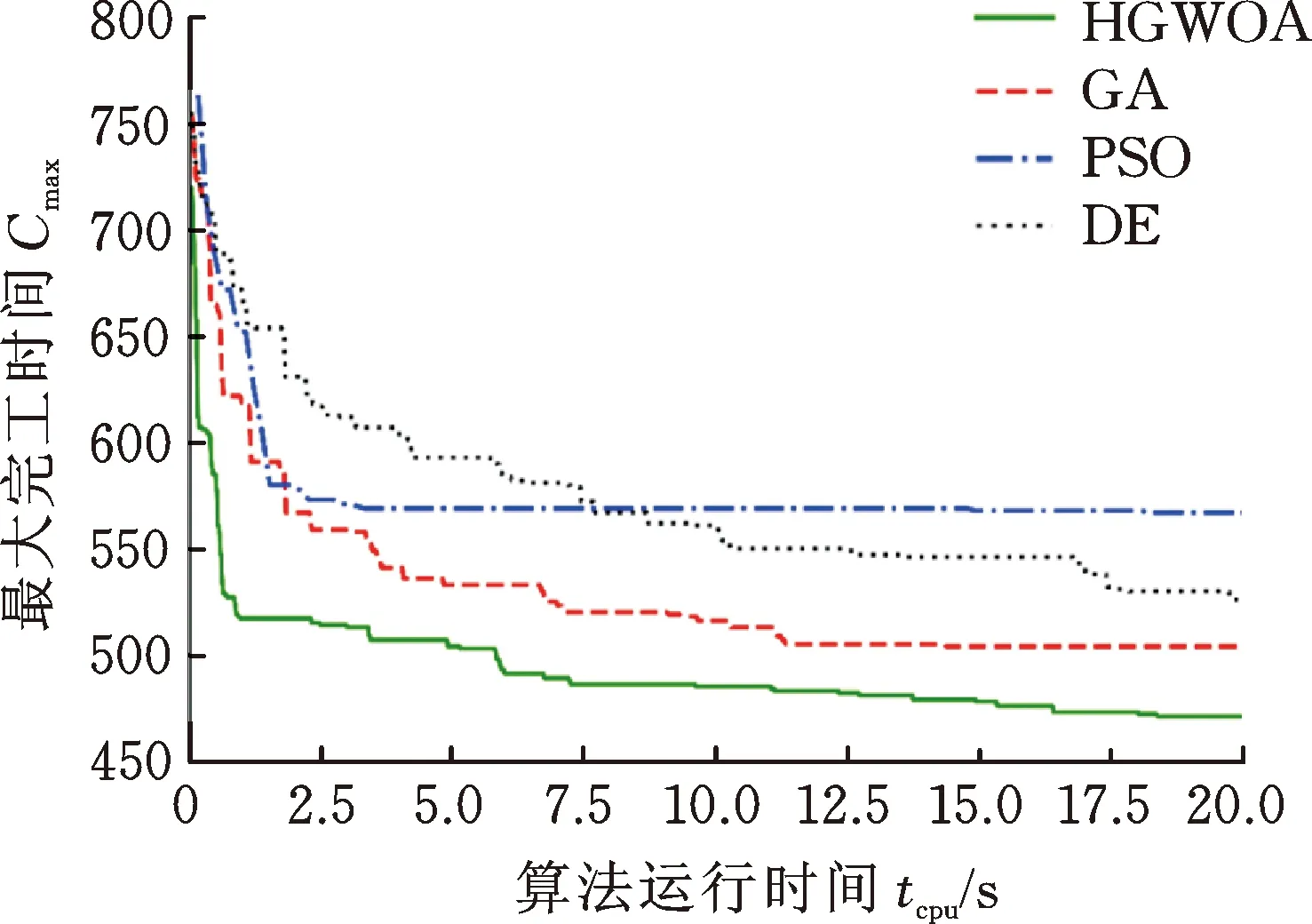
(c) MK09_1
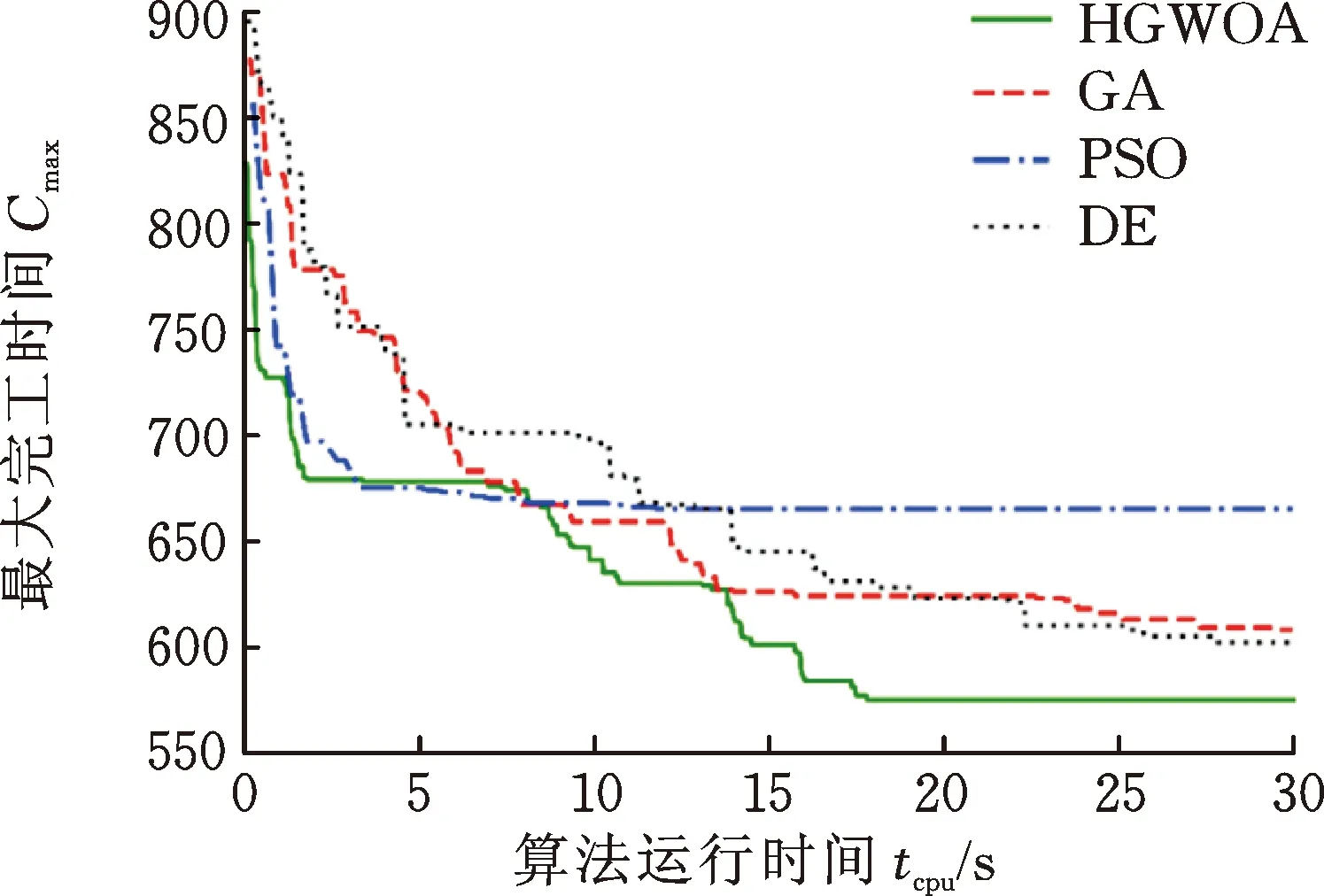
(d) MK15_1图5 收敛曲线示例Fig.5 Convergence curve example
由图5a可知,此次运行HGWOA的初始起点最差,但在算法刚开始运行的一段时间内HGWOA的收敛速度最快,其次是PSO。虽然在一开始PSO的初始条件优于HGWOA,而且收敛速度较快,在算法运行初始阶段一度领先于HGWOA,但 PSO在运行约 0.4 s后就陷入局部最优无法跳出,说明该算法克服陷入局部最优的能力有所欠缺。相比之下,HGWOA不仅在搜索的初期具有较快的收敛速度,而且在后续搜索中具有较好的跳出局部最优的能力。就收敛结果来看,HGWOA获得了最好的结果,GA 次之,PSO最差。
针对上述收敛曲线的融合调度方案甘特图见图6~图8所示(限于篇幅,MK15_1融合调度优化方案甘特图扫OSID二维码可见)。以图6为例具体说明。图6a为HGWOA所获得的 MK01_1 算例最优解Cmax=47时的机器加工任务调度甘特图,图中每一个方块代表一道工序,方块内上方数字表示工件号,下方数字表示工序号,由图可知各工序加工顺序安排以及机器的选择。图6b是图6a对应的AGV运输任务调度甘特图,图中“C”、“Z”、“X”分别代表充电站、装载站和卸载站,每一个方块代表一个AGV运输任务,方块内上方数字代表起点机器序号,下方数字则为终点机器序号。
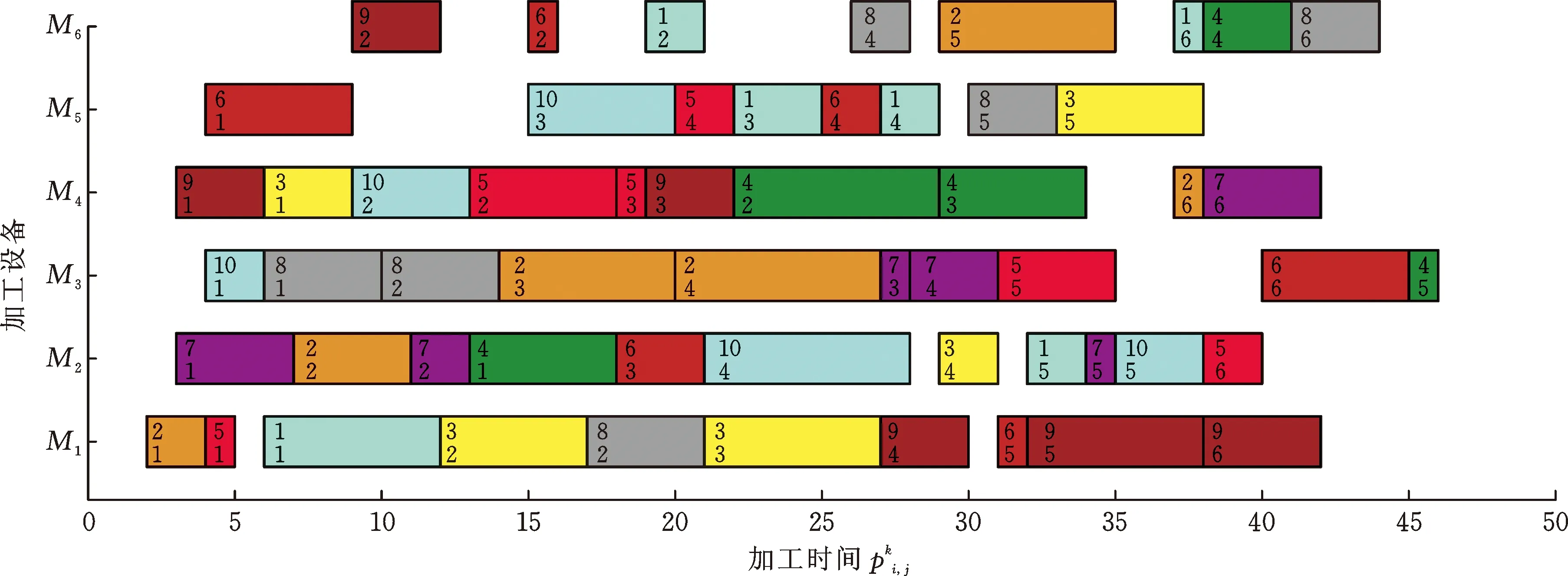
(a) 机器加工任务调度甘特图

(b) AGV运输任务调度甘特图图6 MK01_1融合调度优化方案甘特图Fig.6 MK01_1 fusion scheduling optimization plan Gantt chart
4 结束语
本文研究了考虑AGV运输工件的柔性作业车间AGV融合调度问题,以最小化最大完工时间为优化目标建立了相应的数学模型并提出改进鲸鱼优化算法进行了求解。在所提鲸鱼优化算法中所做的改进包括设计编码和解码方案、引入混合初始化策略、交叉和变异方法、嵌入局部搜索等操作,提升了算法的寻优能力。最后,将传统的15个标准算例扩展成为30个案例,将HGWOA与常用算法进行了对比试验,对比结果验证了改进算法的合理性和有效性。
文中所建立的作业车间AGV融合调度模型未考虑AGV差异性,即运输速度、单次充电运输距离、充电时间等因素,与实际的生产制造系统存在差异,后续的融合调度优化研究将重点考虑这些实际生产因素,并不断改进和完善多目标的求解算法,以进一步丰富现在作业车间AGV融合调度优化方案。
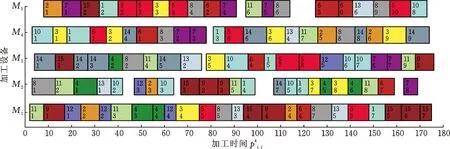
(a) 机器加工任务调度甘特图
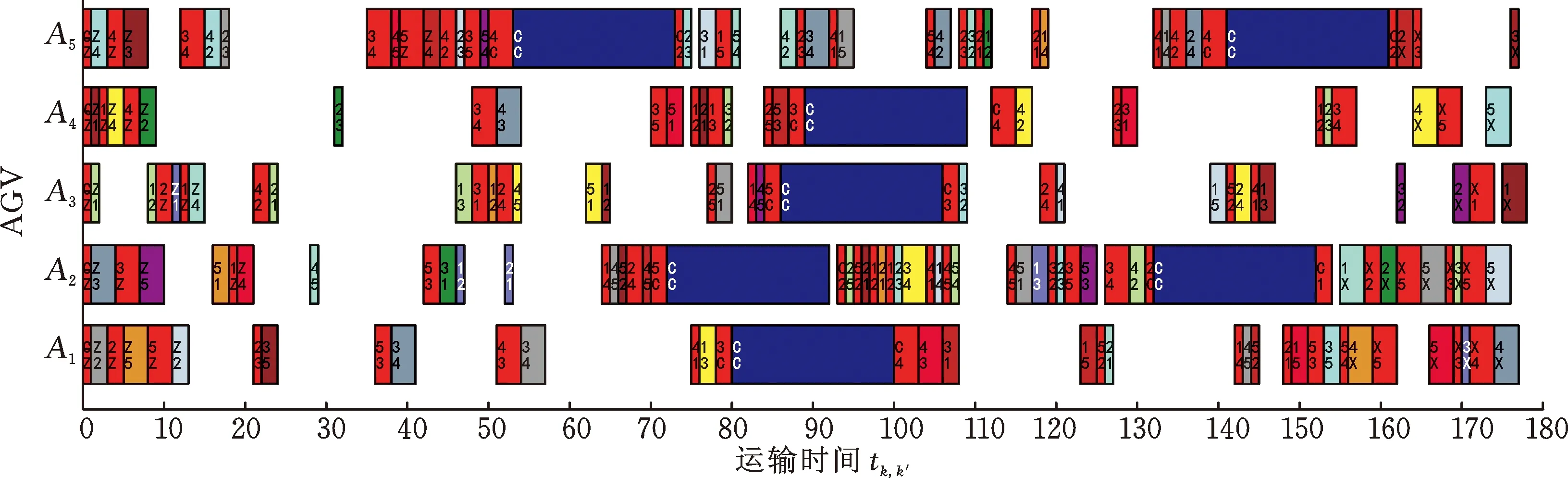
(b) AGV运输任务调度甘特图图7 MK05_1融合调度优化方案甘特图Fig.7 MK05_1 fusion scheduling optimization plan Gantt chart
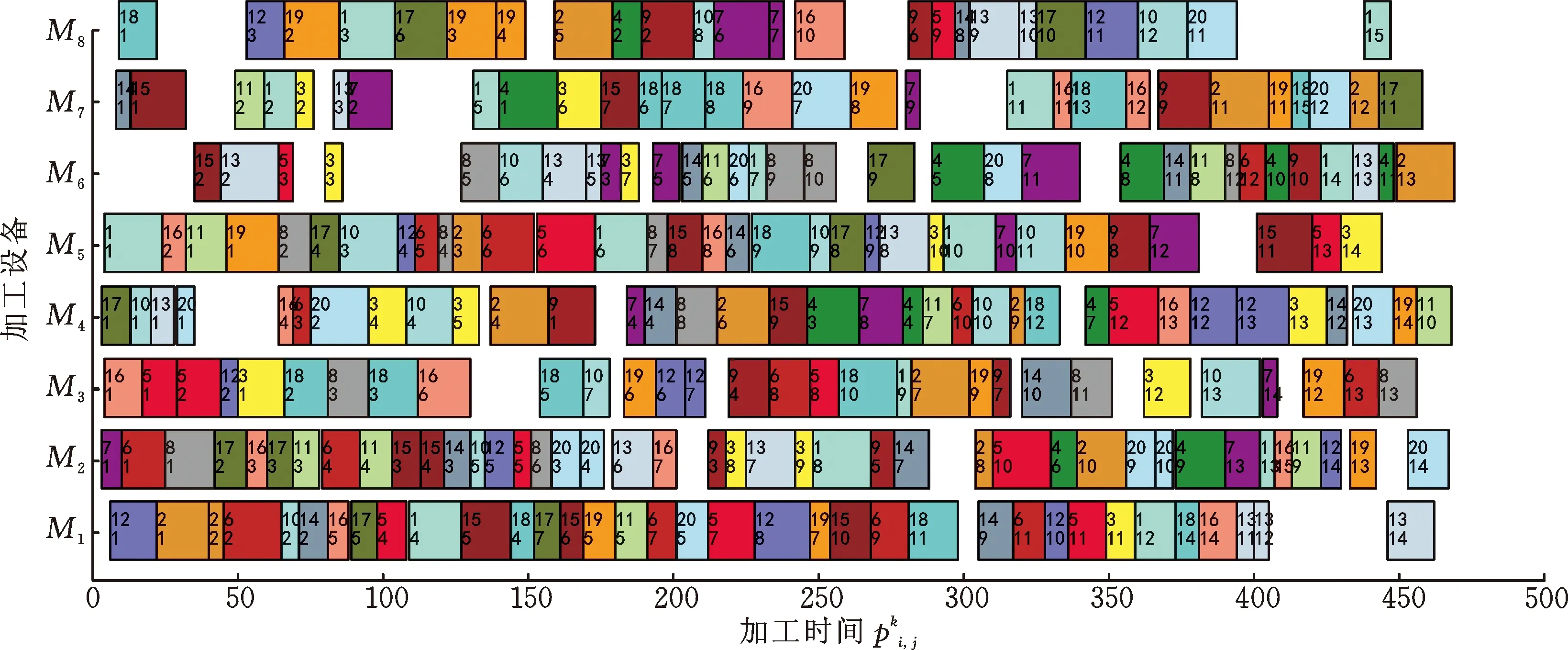
(a) 机器加工任务调度甘特图
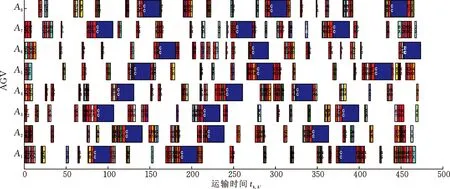
(b) AGV运输任务调度甘特图图8 MK09_1融合调度优化方案甘特图Fig.8 MK09_1 fusion scheduling optimization plan Gantt chart
