磁轴承激励下转子系统动力学特性

李胜远 郑龙席

西北工业大学动力与能源学院，西安，710072

0 引言

高压压缩机转子系统的稳定性主要受到油膜轴承和密封动力学参数的影响[1]。高密度工作介质和高转速使密封的交叉刚度系数显著增大，因此转子系统的稳定性评价在高压压缩机的研制中具有重要意义[2-3]。

在API 617标准[4]中，使用一阶正进动模态的对数衰减率来评价压缩机转子系统的稳定性。使用磁轴承在轴端进行扫频激励进而获得对数衰减率的方法在高压压缩机转子系统的稳定性评估中应用广泛。磁轴承主要由电磁铁、控制器、传感器和功率放大器组成，通过电磁铁线圈中的电流产生可控电磁力。相比于传统的机械轴承，磁轴承具有无接触、低机械磨损、噪声小和寿命长等优点[5]。BAUMANN[6]在额定转速下应用磁轴承对转子系统施加了单向简谐扫频激励力，发现转子系统的反进动和正进动模态均被激发。TAKAHASHI等[7]也采用通过磁轴承施加单向简谐扫频激励力的方法，并应用单向频率响应函数在频域内识别了转子系统一阶正进动模态的对数衰减率。MOORE等[8-9]通过磁轴承对转子系统施加了仅激发正进动模态的激励力，并评估了高压压缩机转子系统的稳定性裕度。BIDAUT等[10]利用磁轴承在两个正交方向上分别施加简谐扫频激励力，并通过控制两个激励力之间的相位差激发了转子系统的反进动或正进动模态。SOROKES等[11]、SOULAS等[12]和PETTINATO等[13]也分别应用磁轴承激励的方法测试了高压压缩机转子系统的稳定性。由上述文献可知，在不同类型磁轴承激励力的作用下，转子系统的反进动和(或)正进动模态被激发。然而，从目前公开发表的文献看，对磁轴承激励下转子系统动力学特性的详细分析较少。

为分析磁轴承激励下转子系统的振动机理，本文应用一维有限元方法建立双盘转子系统动力学特性计算模型，研究在不同类型磁轴承激励下转子系统的动力学行为。

1 转子系统有限元建模

1.1 转子轴段的有限元离散

本文采用一维有限元方法对转子系统动力学建模，采用Timoshenko梁单元以考虑轴段转动惯量和剪切变形的影响。仅考虑转子系统的弯曲振动，转子轴的有限元离散如图1所示。其中OZ轴为转子系统的旋转轴，第i个转子轴段的广义坐标向量为qi=(uivi,θX,i,θY,i,ui+1vi+1,θX,i+1,θY,i+1)T，(ui,vi)和(θX,i,θY,i)分别为第i个节点沿X轴和Y轴的横向位移和转角。转子轴段的局部单元矩阵可由Lagrange方程获得[14-15]：

(1)

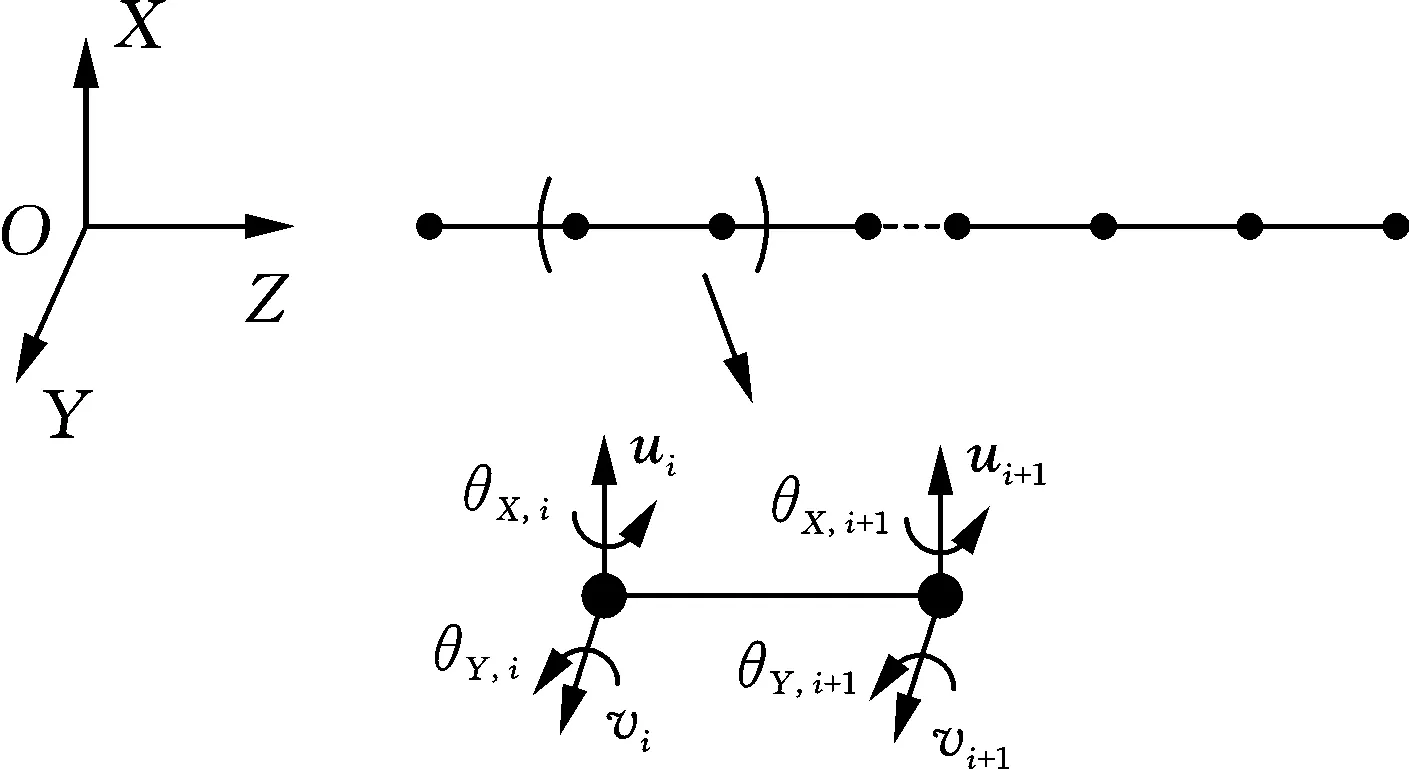
图1 转子轴的有限元离散Fig.1 Finite element discretization of rotor shaft

分别将T和U代入式(1)可得轴段单元的质量矩阵、陀螺矩阵和刚度矩阵。假设圆盘为刚性盘，忽略其应变能，将圆盘的动能代入式(1)可得圆盘的质量矩阵和陀螺矩阵。对于支承轴承，假设其具有线性的载荷变形关系，由于轴承主要承受径向载荷，所以只考虑横向的刚度和阻尼系数。轴承作用在转子系统上的载荷可写为轴承处转子位移和速度的函数[16-17]：

(2)

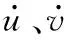
1.2 磁轴承激励下转子系统动力学响应

转子系统的运动微分方程为[18-19]：

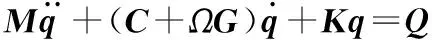
(3)

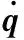
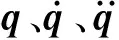
若通过磁轴承在转子系统的l节点处施加不平衡力形式的激励力，则该激励力与转子同向旋转，且在4l-3、4l-2、4l-1、4l自由度处激励力的分量Q1为[20]

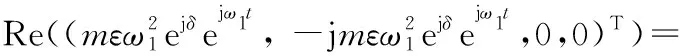
(4)

式中,m为不平衡质量;ε为偏心距;δ为相对于X轴正方向不平衡量的相位;ω1为该激励力的角速度。

若在l节点处施加角速度为ω2的反向旋转激励力，则激励力向量Q2为

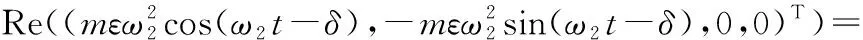
(5)

若通过磁轴承在l节点的X和Y方向上作用角速度为ω3的简谐激励力，则激励力向量Q3为

Q3=(rcos(ω3t),scos(ω3t+α),0,0)T=
Re((rejω3t,sejω3tejα,0,0)T)=Re(ejω3t(r,sejα,0,0)T)

(6)

式中,r、s分别为X和Y方向上激励力的大小；α为X、Y两个方向上激励力的相位差。

根据式(4)～式(6)中激励力的形式，设作用在转子系统上激励力和响应的形式分别为Qi=Re(Q0ejωit)和qi=Re(q0ejωit)，i=1,2,3，Q0为X和Y方向上激励力的大小和初相位，q0为复数。将Qi和qi代入式(3)可得

(7)

设复数q0的表达式为

q0=a+bj=|q0|ejβ

(8)

对于激励力向量Qi，转子系统的响应qi为

qi=Re(|q0|ej(ωit+β))=|q0|cos(ωit+β)

(9)

由式(9)可知，复数q0的模|q0|为磁轴承激励下转子系统各个自由度的响应幅值；相位β为各个自由度的响应相位。

2 转子系统计算模型

本文研究的双盘转子系统及轴段的有限元离散模型如图2所示。转子总长为1.2 m，相邻节点间的间隔为0.2 m，转轴直径为40 mm，转速为3000 r/min。轴承支承在转子两端，两个轴承的直接刚度系数kuu和kvv均为1 MN/m，直接阻尼系数cuu和cvv均为100 N·s/m，交叉刚度系数kuv和kvu以及交叉阻尼系数cuv和cvu均为零。以左端轴承为0位置，圆盘D1和D2分别位于0.4 m和0.8 m处。圆盘的厚度为50 mm，圆盘D1和D2的直径分别为300 mm和200 mm。转轴和圆盘材料的弹性模量E=211 GPa，剪切模量G=81.2 GPa，密度ρ=7810 kg/m3。

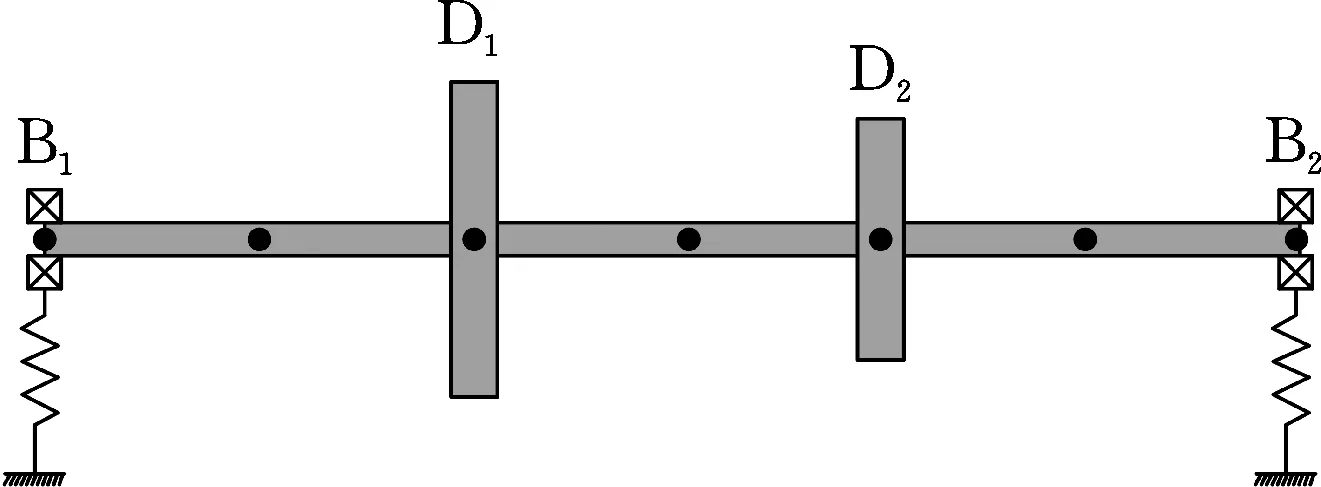
图2 双盘转子系统计算模型Fig.2 Calculation model of a double-disk rotor system

3 计算结果

3.1 转子系统固有频率和模态振型分析

图3为该转子系统的Campbell图。当转子转速为3000 r/min时，转子系统的前两阶反进动固有频率分别为18.51 Hz和58.87 Hz，前两阶正进动固有频率分别为18.84 Hz和65.27 Hz。从图3中可以看出，由于陀螺矩阵的作用，随着转速的增大，正进动固有频率逐渐增大，反进动固有频率逐渐减小，所以同阶反进动/正进动固有频率线随着转速的增大有相互分离的趋势。

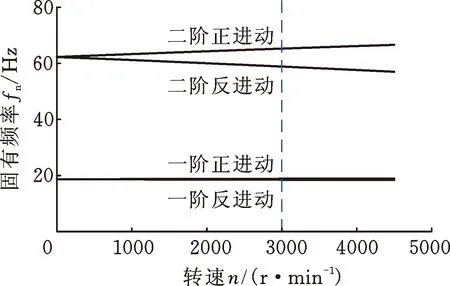
图3 转子系统的Campbell图Fig.3 Campbell diagram of the rotor system

由于同阶反进动/正进动固有频率较为接近，因此同阶反进动/正进动的模态振型相似。图4显示了当转速为3000 r/min时，转子系统的前两阶正进动模态振型。对于一阶反进动/正进动模态振型，转轴进动轨道呈U形，两个圆盘的变形方向相同；而对于二阶反进动/正进动模态振型，转轴进动轨道呈S形，两个圆盘的变形方向始终相反。

(a) 一阶正进动模态振型(fn=18.84 Hz)

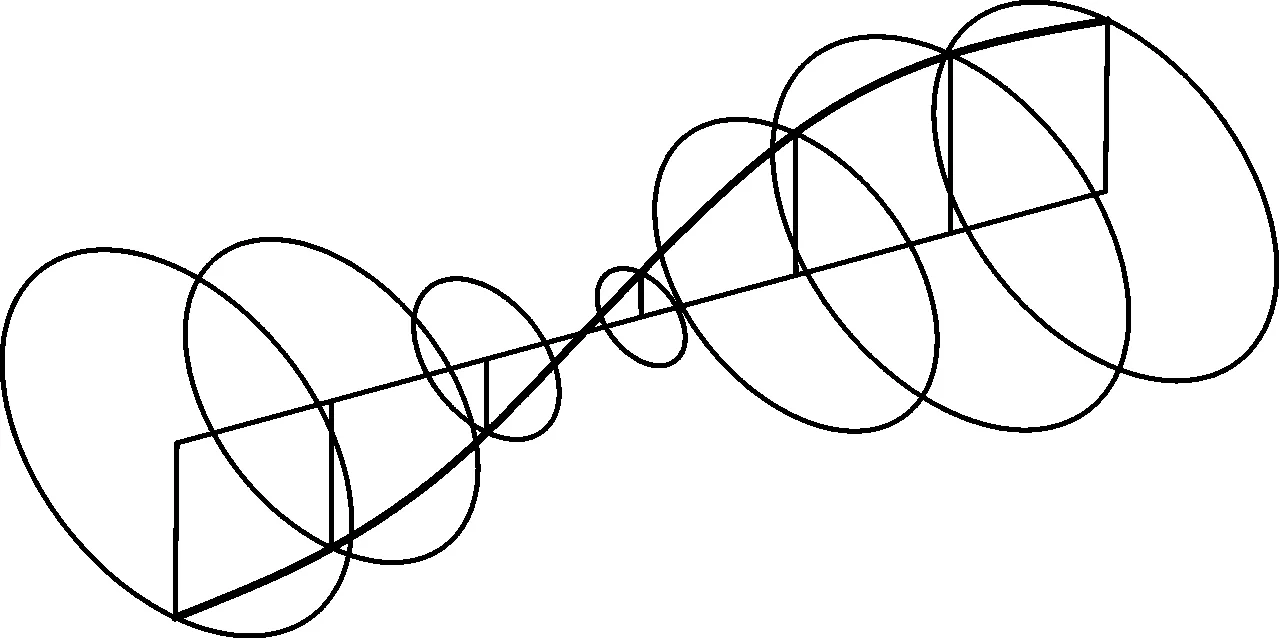
(b) 二阶正进动模态振型(fn=65.27 Hz)图4 转速为3000 r/min时，转子系统的前二阶正进动模态振型Fig.4 First two forward mode shapes of the rotor system when the spin speed is 3000 r/min

3.2 同向/反向旋转激励下转子系统动力学响应

当转子转速为3000 r/min，通过磁轴承在转子跨中位置处施加由100 g·mm、0°相位的不平衡量引起的同向旋转激励力时，圆盘D1和D2的响应幅值如图5所示。从图中可以看出，在所研究的激励频率范围内，圆盘响应中出现了两个响应峰值，与图3比较可知，响应峰值对应的频率等于转速为3000 r/min时转子系统的前两阶正进动固有频率，因此，同向旋转的扫频激励力激发了转子系统的正进动模态。

图6显示了在响应峰值处圆盘的进动状态，其中“×”表示轨迹起点，“◇”表示轨迹终点，逆时针表示正进动，顺时针表示反进动。从图6可以看出，在两个响应峰值处，圆盘均为正进动，且进动轨迹为圆形。在一阶正进动固有频率处两个圆盘的进动相位相同，而在二阶正进动固有频率处两个圆盘的进动相位相反，这与图4是一致的。

当通过磁轴承在转子跨中位置处施加反向旋转的激励力时，在不同的激励频率下，两个圆盘的响应幅值如图7所示。与图3比较可知，圆盘响应峰值对应的频率等于转速为3000 r/min时转子系统的前两阶反进动固有频率。图8显示了在响应峰值处两个圆盘的进动状态，可以看出，两个圆盘均为反进动，且进动轨迹为圆形，因此，反向旋转的扫频激励力激发了转子系统的反进动模态。当转子系统反进动时，由于转轴的纤维在进动过程中处于拉伸和压缩的交变状态，可能会导致转轴的高周疲劳以及由轴材料内阻引起的转子失稳，故工程应用中应避免转子系统出现反进动。

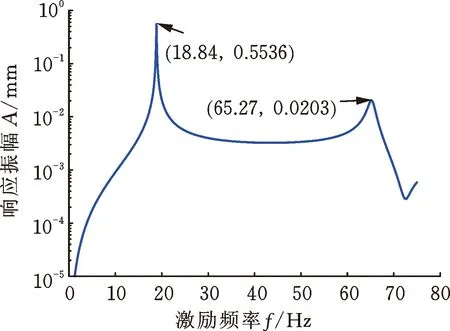
(a) 圆盘D1的响应振幅

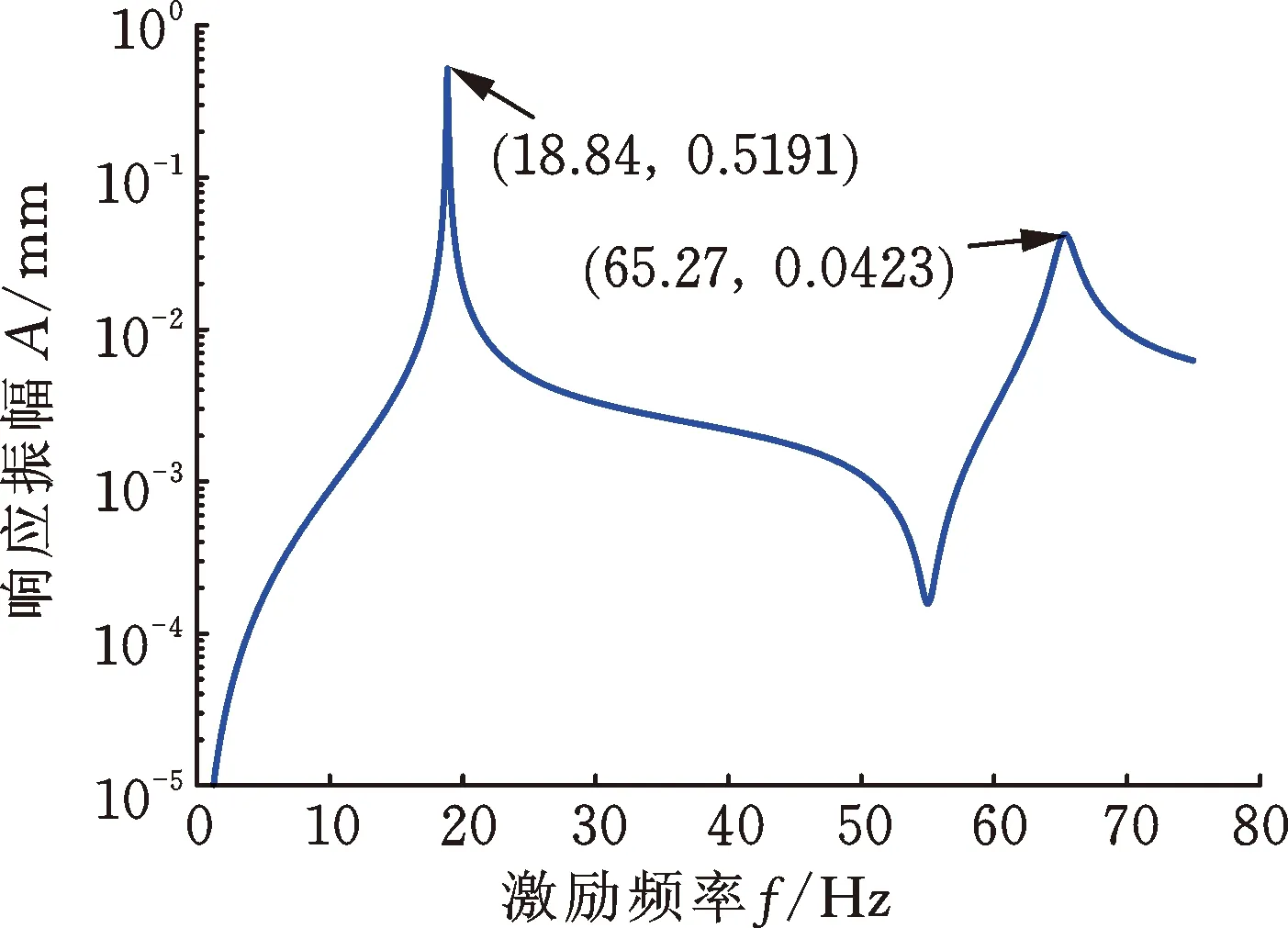
(b) 圆盘D2的响应振幅图5 同向旋转扫频激励力下圆盘的响应Fig.5 Disks response under co-rotating sweep exciting force

(a) 一阶正进动固有频率

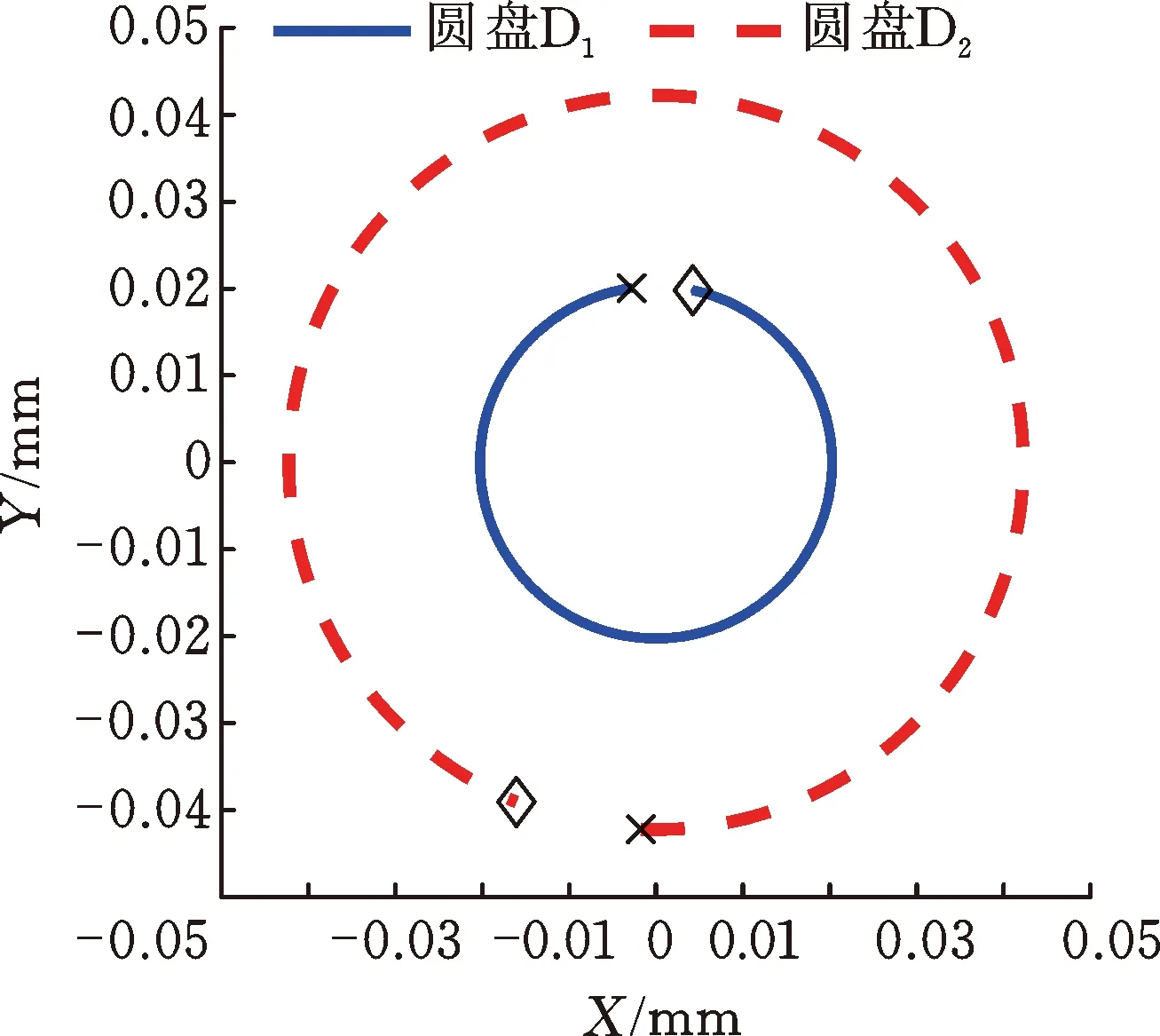
(b) 二阶正进动固有频率

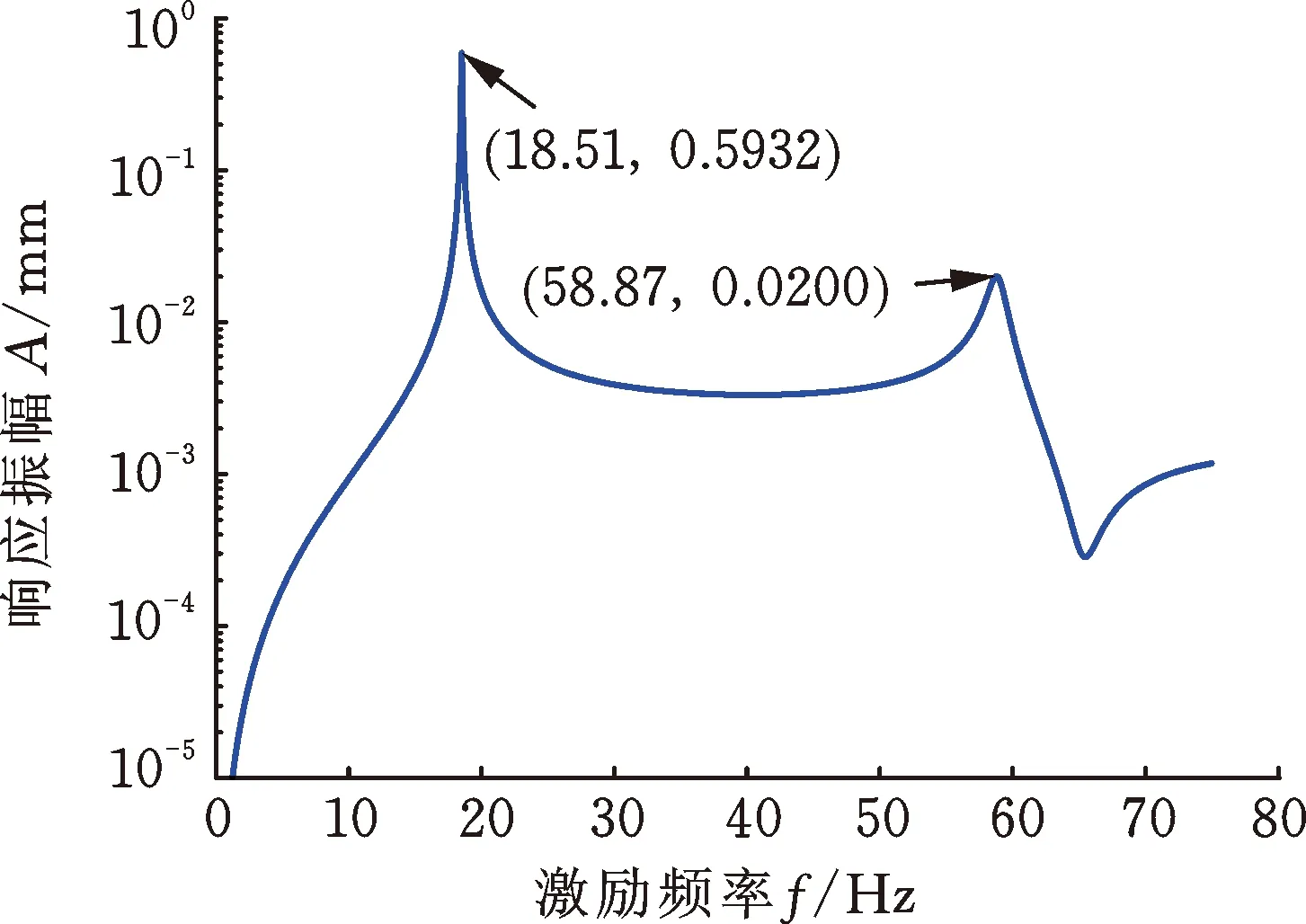
(a) 圆盘D1的响应振幅

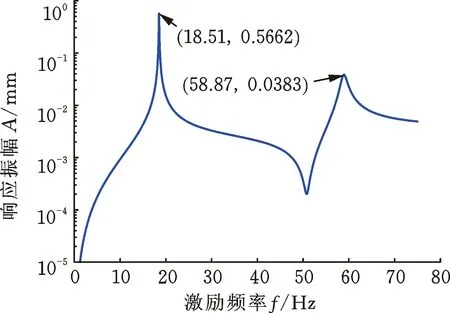
(b) 圆盘D2的响应振幅图7 反向旋转扫频激励力下圆盘的响应Fig.7 Disk response under counter-rotating exciting forces

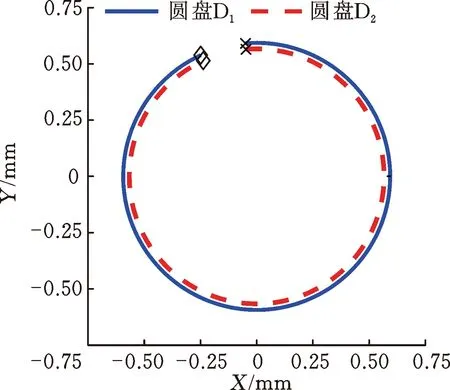
(a) 一阶反进动固有频率

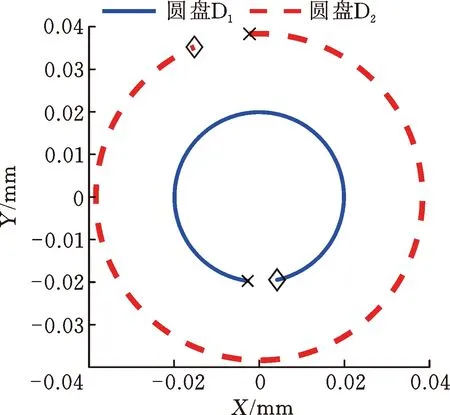
(b) 二阶反进动固有频率

3.3 单向简谐扫频激励下转子系统动力学响应

当转子转速为3000 r/min时，通过磁轴承在转子跨中位置处的X方向施加简谐激励力QX=(cosωt,0,0,0)T，两个圆盘的响应幅值如图9所示。此时，响应峰值对应的频率等于转速为3000 r/min转子系统的反进动/正进动固有频率，转子系统的反进动/正进动模态均被激发，原因如下：由欧拉公式可知cosωt=0.5(ejωt+e-jωt)，因此作用在转子系统上的单向简谐激励力可以等效为同向旋转激励力QX1=0.5(cosωt,sinωt,0,0)T和反向旋转激励力QX2=0.5(cos(-ωt),sin(-ωt),0,0)T之和，二者分别激发了转子系统的正进动/反进动模态;当对转子系统分别施加激励力QX1和QX2时，计算所得的响应之和与图9相同，从而验证了上述分析的准确性。

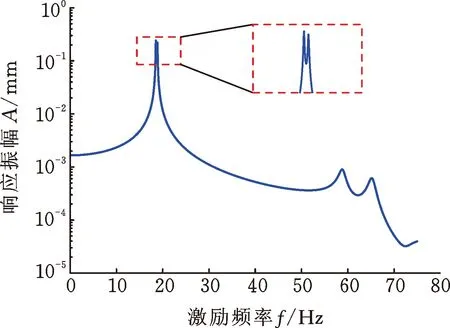
(a) 圆盘D1的响应振幅

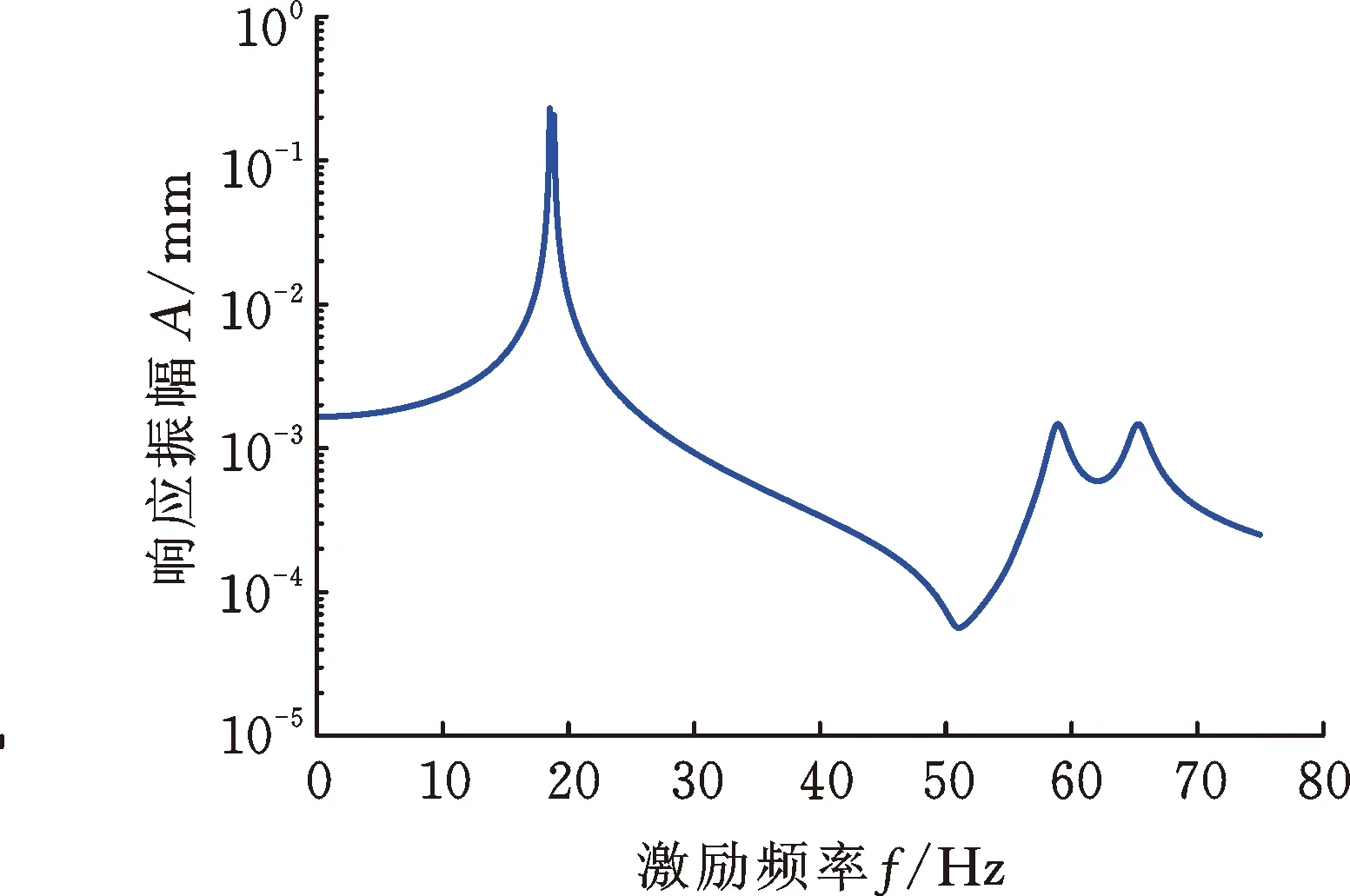
(b) 圆盘D2的响应振幅图9 单向简谐扫频激励下圆盘的响应Fig.9 Disk response under unidirectional harmonicsweep excitation

图10显示了响应峰值处圆盘的进动状态，可以看出，由于陀螺力矩的耦合作用，故X方向的激励使Y方向出现了响应幅值。由于两个方向的响应幅值存在差异，因此转子系统的进动轨迹为椭圆形。

在不同的转速下，通过磁轴承在转子跨中位置施加简谐激励力QX=(cosωt，0，0，0)T，转子系统的瀑布图见图11。由上述分析可知，此时转子系统的反进动/正进动模态均被激发，由于一阶反进动/正进动固有频率在低转速时较为接近，因此在瀑布图中的一阶反进动/正进动固有频率处未出现明显的双共振峰。由于陀螺力矩使二阶反进动/正进动固有频率的差值随着转速的增大而逐渐增大，所以从瀑布图中可以看出二阶反进动/正进动固有频率线随着转速的增大逐渐分离，且在较大转速时的二阶反进动/正进动固有频率处均出现明显的共振峰。本节得到的转子系统在单向简谐扫频激励下的进动状态与文献[5-6]中的实验结果相同，从而验证了本文磁轴承激励下转子系统动力学建模的准确性。

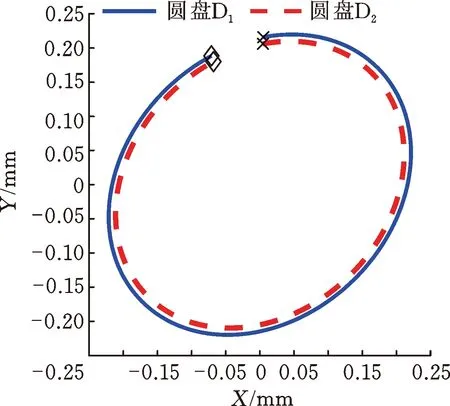
(a) 一阶反进动固有频率

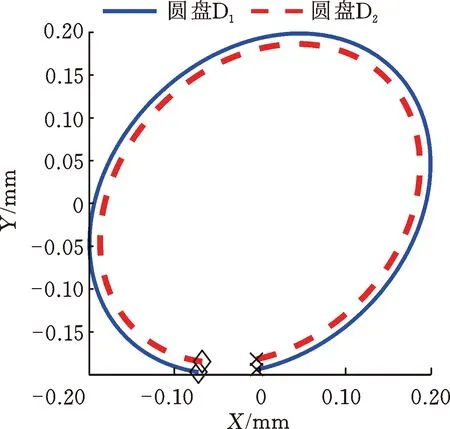
(b) 一阶正进动固有频率

(c) 二阶反进动固有频率

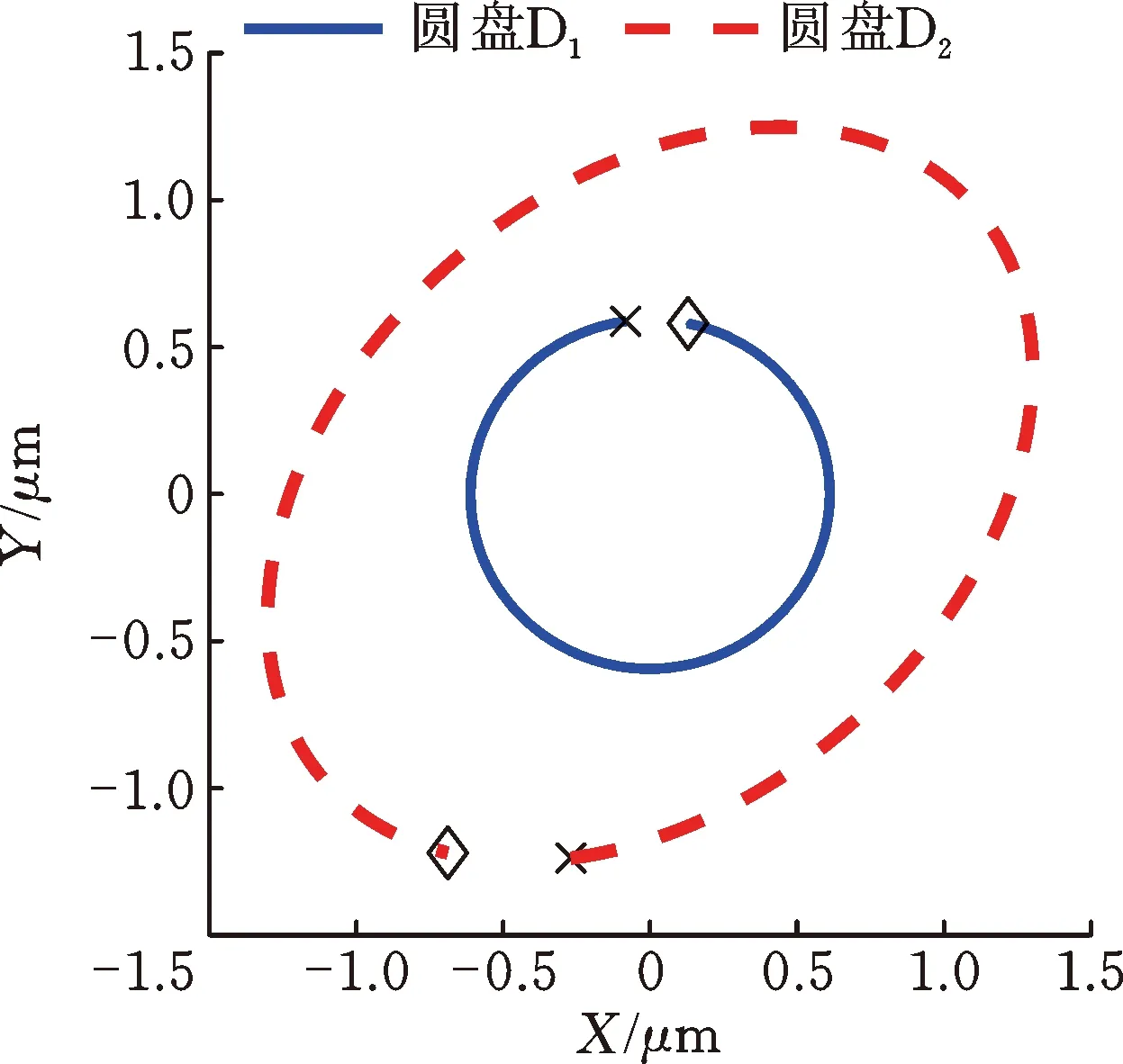
(d) 二阶正进动固有频率

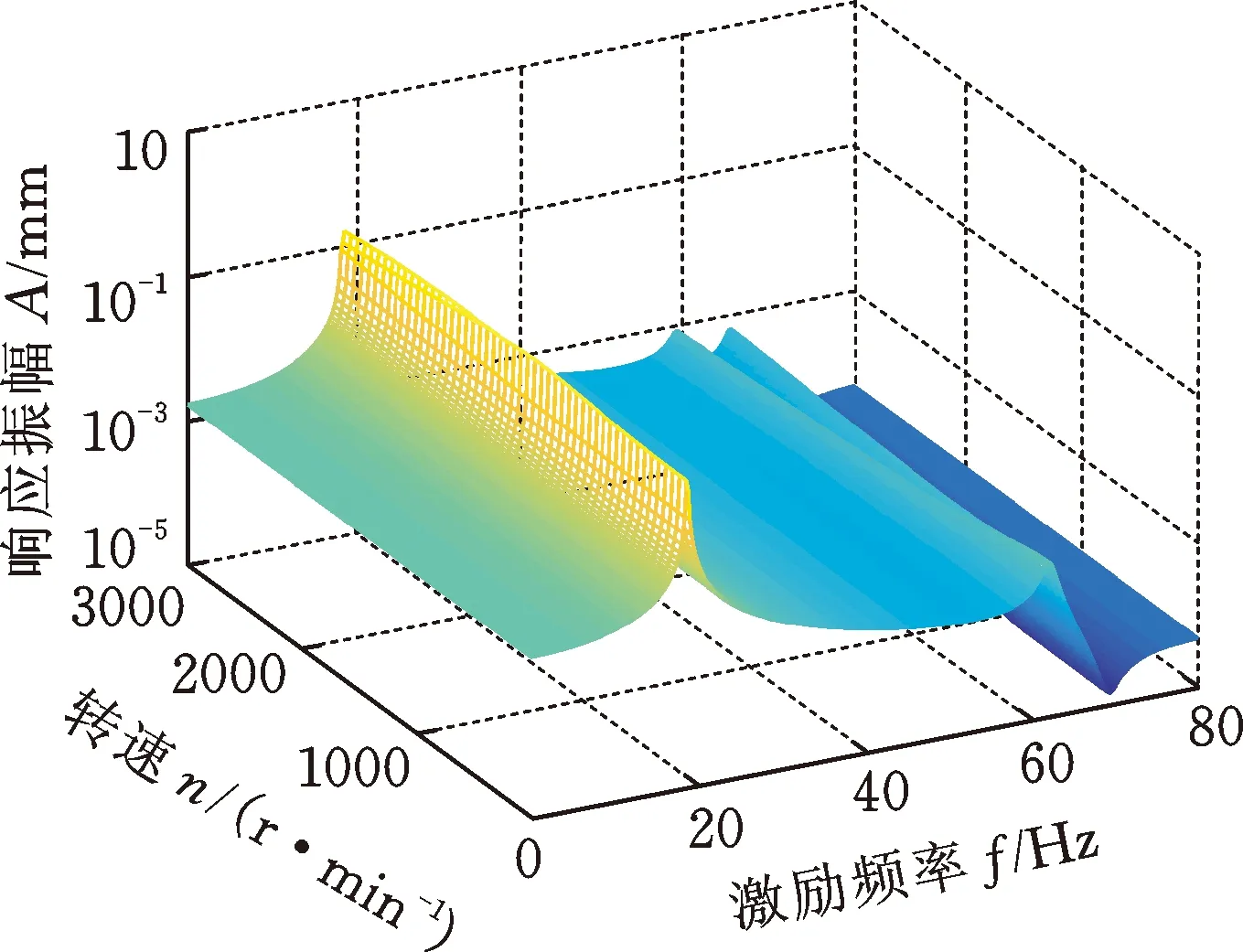
(a) 圆盘D1

(b) 圆盘D2图11 转子系统的瀑布图Fig.11 Waterfall plot of the rotor system

3.4 双向简谐扫频激励下转子系统动力学响应

当转子转速为3000 r/min，通过磁轴承在转子跨中位置的X和Y方向分别施加简谐激励力QX=cosωt和QY=cos(ωt+α)，在不同相位值α下，两个圆盘的进动状态如表1所示。从表中可以看出此时转子系统的进动状态取决于两个方向上激励力的相位差。当相位差为π/2或3π/2时，转子系统的反进动或正进动模态被激发，转子系统以圆轨迹进动；而相位差为其他值时，转子系统的反进动/正进动模态均被激发，转子系统以椭圆轨迹进动。由此可知，在使用磁轴承对转子系统做双向简谐扫频激励时，两个方向上激励力相位差的选取是至关重要的。

表1 激励力相位差对转子系统进动状态的影响Tab.1 Effect of the phase difference of the excitation force on the whirl state of the rotor system

4 结论

(1)同向旋转的扫频激励力激发了转子系统的正进动模态，而反向旋转的扫频激励力激发了转子系统的反进动模态，两种情况下转子系统均以圆轨迹进动。

(2)单向简谐激励力可以分解为同向旋转激励力和反向旋转激励力之和，因此在单向简谐扫频激励力作用下，转子系统的反进动/正进动模态均被激发，转子系统以椭圆轨迹进动。

(3)在双向简谐扫频激励力作用下，转子系统的进动方向和进动轨迹取决于两个激励力的相位差。