第20届亚洲物理奥林匹克竞赛理论试题3介绍与解答

(清华大学物理系,北京 100084)

第20届亚洲物理奥林匹克竞赛于2019年5月5日至13日在澳大利亚阿德莱德举行。由清华大学物理系率领代表中国参赛的8名中学生获得了总共9枚金牌中的6枚[1],取得了相当优秀的成绩。与往年相比,本次竞赛的题目难度较大,整体成绩偏低,按既定规则给出的金牌数与奖牌数都大幅度少于往届(例如2014—2018年每届金牌数平均为32枚)。本次竞赛理论试题共三道,每道10分。其中第三道关于翻转陀螺的问题[2]很有意思。翻转陀螺对于很多人并不陌生,在网上可以买到玩具,网上还有玻尔和泡利兴致勃勃玩翻转陀螺的照片。它在我国的力学教材中也有提到[3],但多是定性或半定量说明,缺少模型简化与详细计算。在本次竞赛中,出题委员会将翻转陀螺进行了模型简化,考查参赛者对于力学中转动与坐标变换等基本知识点的掌握与计算能力,把一个玩具变成一道正统而有趣的物理题目。从竞赛结果看,本题有一定难度,在三道理论题中其平均分数最低,所以值得对它进行详细的介绍与解答。

1 翻转陀螺试题介绍

翻转陀螺指的是一种特殊的陀螺,它被转动后可以自行翻转。我们可以将它模拟为一个半径为R的球体,有一端被切除后,加上一根短杆,总质量为m。它具有对应与穿过短杆的轴的旋转对称性,该轴与竖直方向成一夹角θ。沿着此对称轴,从其质心C到几何中心O的直线距离为αR,如图1(a)所示。翻转陀螺与地面的接触点为A;我们假设地面是平面的,并将其称为地板。在某些特定的几何约束条件下,若在最初时,使它旋转得足够快,则翻转陀螺将会倾斜。导致短杆越来越向下偏,直到以杆为支撑继续旋转,最终停下。

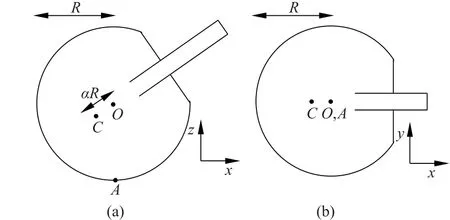
图1 翻转陀螺视图

以xyz代表中间(intermediate)转动参考系,其轴固定且向上,陀螺的对称轴是在xz-平面。图1 所示为翻转陀螺的侧视图与俯视图。如图1(b)所示,当俯视时,陀螺的对称轴沿着x轴。

如图2所示的是陀螺开始转动后,在几个不同阶段的运动情况:

(a) 阶段Ⅰ:初始刚开始转动后瞬间,角度θ～0

(b) 阶段Ⅱ:不久后,角度以倾斜下偏,角度0＜θ＜π

(c) 阶段Ⅲ:当短杆初次触地,角度θ＞

(d) 阶段Ⅳ:翻转后,陀螺以杆为支撑做旋转,角度θ～π

(e) 阶段Ⅴ:在最后阶段,陀螺静止停在杆上,θ=π。

以XYZ代表惯性参考系,支撑陀螺的地面完全在XY平面。参考系xyz的定义如前所述,将XYZ系统绕Z轴转动角度φ后,即与xyz重合。由XYZ系到xyz的转换如图3(a)所示,其中

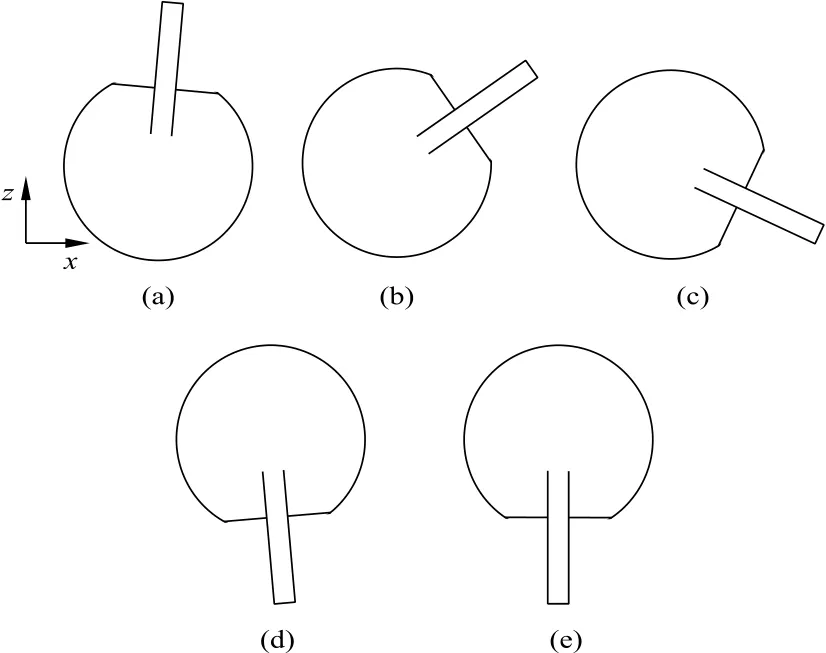
图2 阶段Ⅰ～Ⅴ的陀螺运动,图示为xz 平面

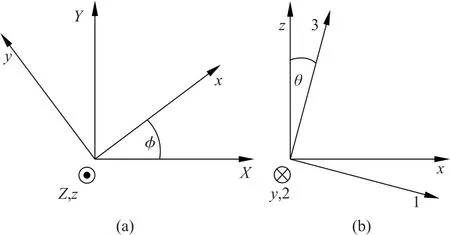
图3 两参考系之间的转换

在三维空间的任何转动可用3 个欧拉角（θ,φ,ψ）来描述。惯性系XYZ,介乎中间的参考系xyz与陀螺参考系(也叫随体参考系)123之间的转换,可利用欧拉角来了解。

在我们对翻转陀螺运动的描述中,角度θ和φ分别是球坐标系中的标准天顶角(zenith angle)和方位角(azimuthal angle)。在XYZ系中,它们的定义如下:θ是竖直轴Z到陀螺对称轴的夹角,它代表短杆偏离竖直方向的角度;而φ则代表陀螺绕Z轴转动的角位置,它的定义是XZ-平面与O,A,C所在平面(即陀螺对称轴的竖直投影)之间的夹角。第三个欧拉角ψ描述的是陀螺绕其自身对称轴的旋转,即“自转”,其对应的角速度为

旋转的陀螺参考系被定义为一个新的转动参考系123,此参考系可由xyz系绕轴转一角度θ而获得;就是使轴往下“倾斜”一个角度θ后,与陀螺的对称轴重合。由xyz系到123系的转换如图3(b)所示,其中

翻转陀螺的运动是很复杂的,它涉及三个欧拉角随时间的变化,以及陀螺的平移速度(或位置)和陀螺对称轴的运动。所有这些参数互相耦合。因此要解这样的问题,需要标准工具,包括使用牛顿定律写出系统的方程,然后计算机编程用数值方法求解。

在此,要求探究翻转陀螺的物理并建立方程组,但不用数值求解。

翻转陀螺和它运动时所接触地面之间的摩擦力是其运动的驱动力。假设翻转陀螺在点A处与地板保持接触,直到短杆接触地板为止。陀螺在点A相对于地板的速度为VA。陀螺与地板之间的滑动摩擦系数为μk,因为摩擦力|Ff|=μkN,此处,N为正压力的大小。假设最初只令陀螺自旋,即没有受到任何平移的冲量。

以m表示陀螺的质量,I3表示绕对称轴的转动惯量,I1=I2表示绕另外两互相垂直轴的转动惯量。设s是质心的位置向量,且a=是由质心到接触点的向量。

除非特别说明,否则请用xyz参考坐标系作答以获得满分。除非另有说明,否则所有力矩和角动量均相对于质心C。答案中可用N表示。除了A.8部分,只需考虑当θ＜π时的陀螺,并且短杆不与地面接触。

A.1(1分)求此翻转陀螺所受的总外力Fext。画出此陀螺在xz和xy平面上的受力图,在xy平面图上指出VA的方向。

A.2(0.8分)求此翻转陀螺相对于质心的总外力矩τext。

A.4(0.8分)求陀螺相对质心C旋转的总角速度ω,以欧拉角的时间导数:,和来表示。使用图3分别给出在xyz参考系以及123参考系中的答案。

A.5(1分)用vx,vy和欧拉角的时间导数,来表示翻转陀螺的旋转总能量。若是用来表示,答案也可得部分分数。

A.6(0.4分)求出相对z轴的角动量的变化率。

A.7(1.4分)什么力抵抗重力做功? 求陀螺的能量的瞬时变化率的表达式,用VA表示。给出造成A.5中的能量变化的力和力矩的分量。

A.8(2分)关于陀螺在图2中所示的五个阶段I至V 的运动,在答案纸中定性地描绘以下能量项作为时间的函数:总能量ET,重力势能UG,平移动能KT,旋转动能KR。你所描述的能量轴不需要按比例绘制。

A.9(0.5分)证明角动量L和角速度ω在垂直于方向的分量成正比,也就是:并求正比系数k。

结合A.1、A.2及接下来的结果可推出正压力N的大小以及方程组,和欧拉角,A点速度的分量vx、vy、对称轴的单位向量,及它们的时间导数有关。此系统是不可积的,但可用数值方法求解。

运动积分是守恒量,能够减少系统的维度(也就是需要求解方程的数目)。在封闭系统,典型的守恒量包括能量、动量、角动量,它们可明显简化问题。

A.10(1.7分)由于耗散力和外力矩的作用,可看出翻转陀螺的能量和角动量都不守恒。然而有一个相关的量,称为Jellett积分λ,是代表角动量的某一个分量是守恒的,也就是若υ 是某一个向量,则λ=L·υ 不随时间变化。根据你对翻转陀螺的了解以及到目前为止的结果,写出向量υ的表达式,并证明λ的时间导数为0。

2 解答与点评

初看题目似乎显得异常复杂,确实转动问题在力学中是属于较难的部分,其中复杂的原因是因为参考系之间的变换。比如一些物理量在某参考系中容易表达,但是力学方程可能在另一个参考系中更易表达。所以这类问题的关键首先是明了各参考系之间基矢量(base vector)的关系,然后向量在各参考系中的表达就可以互相变换了。这也是为什么题目中首先较详细地定义了实验室参考系XYZ;中间参考系xyz和陀螺自身参考系123,以及用欧拉角给出了各参考系基矢量之间的关系。因而此题的首要任务是先列出各参考系基矢量之间的变换关系。

2.1 基矢量之间的关系

利用图3,可得中间参考系xyz于实验室参考系XYZ,以及xyz与陀螺参考系123之间的关系:

2.2 题目中相关向量的关系式

有了上面基矢量之间的关系,我们可以把向量从一种表达系统地转成题目需要的表达,比如从质心到地面接触点A的向量a

上式中第一行是从图1中容易读出的向量a表达,尽管不是用一个参考系的基矢量;但由基矢量之间的关系,可写出a在xyz系和123系下的表达。

还可导出其他有用的关系式

由题目中给出的关系

可以求得单位向量(基矢量)相对惯性XYZ系的随时变化率

三向量乘积由公式

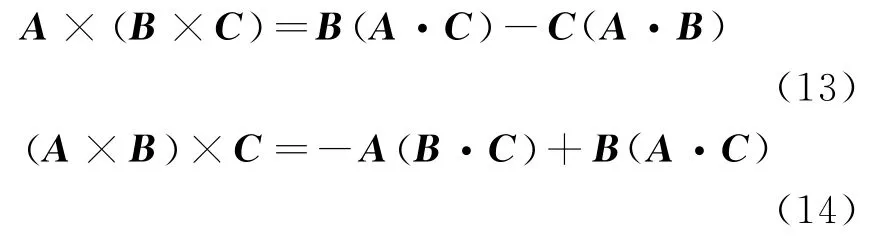
上述关系式将在解题中起到作用,在这里一并列出以方便引用。

2.3 题目解答

A.1问:陀螺所受外力为作用在质心的重力;在接触点A的支持力N和摩擦力Ff(与速度VA反向)。因此有

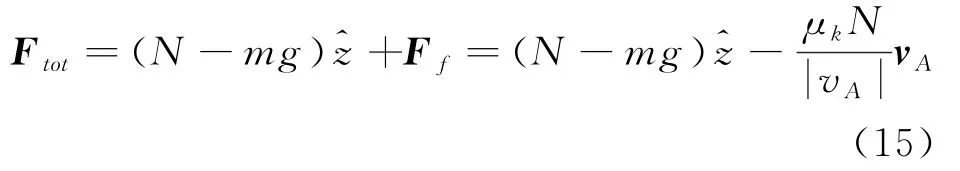
A.2问:陀螺所受外力矩τext(相对质心)为:质心到接触A点的向量a叉乘支持力N和摩擦力Ff

A.3问:由于点A被约束在地面,自然它竖直方向上速度应为0,这是直观的物理图像。在考试前题目研讨中这一点曾被提出,出题者希望参赛者通过给出的约束条件,数学上推导出这一结论:

点A的速度是质心的速度加上A相对质心的速度

接触约束条件

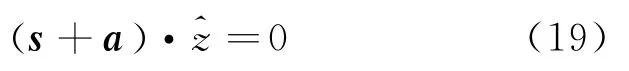
对上式时间求导,a导数用到式(9),并且因此

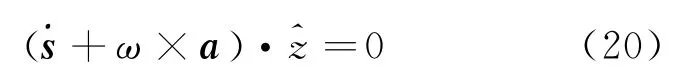
等式的左边正是A点速度的竖直分量。

A.4 问:对于总的角速度向量,最直观地可以先用欧拉角的变化率来表达(参见图3,这也是为何引入中间参考系xyz的原因)

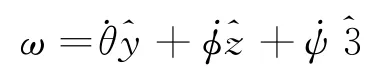
注意这里角速度的分量不是用一个参考系的基矢量表示的,但通过2.1节基矢量的关系,我们现在可以写出ω在xyz系和123系下的表达 (注意

A.5问:陀螺运动的总能量中的动能可以分为质心平动动能Ktrans;绕质心转动的动能Krot;当然别忘了还有重力势能Ug

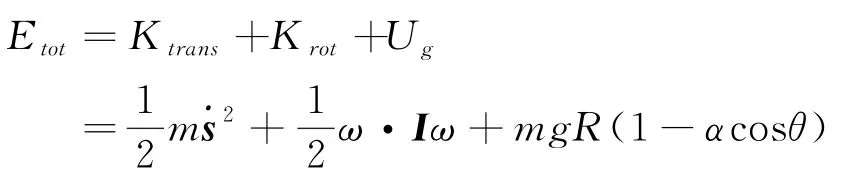
I为转动惯量张量。问题要求用A 点速度分量vx,vy和欧拉角的时间导数来表示。上式中Krot=ω·Iω,代入式(22)即可满足要求;对于,我们可以利用式(18)将其表达为(同时也用到A.3结论,vz=

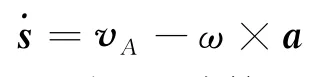
ω×a可由式(18和式3计算

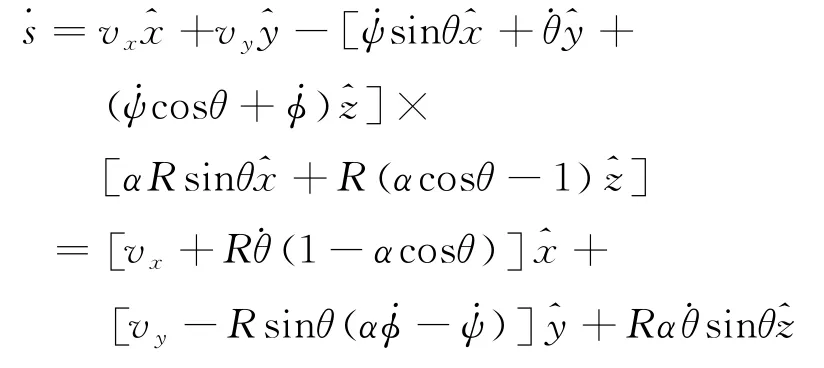
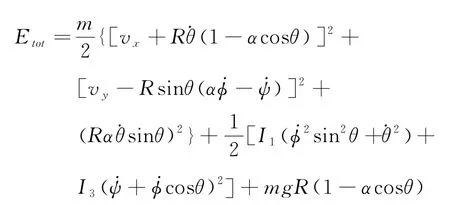
A.6问:利用角动量变化率与力矩的关系,而式(17)给出了外力矩的公式

A.7问:从图2中可看出,过程中陀螺质心略有上升,因而重力势能Ug略有增加。支持力N不做功。只有在A点的摩擦力做功,它使得总能量单调下降。

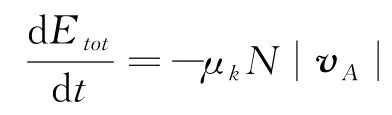
从图2中的Ⅰ到Ⅴ阶段,质心平动动能较小:Ktrans～0;摩擦力主要减小了转动动能Krot,将其部分转化为重力势能,因而是摩擦力抵抗重力做功。开始时角动量主要集中在方向,而使其变化的力从上问式(23)中可看出是摩擦力的y 分量:Ff,y。所以回答本问中在减少转动动能Krot中,Ff,y起主要作用,它的力矩沿方向:a×(从式(17)中可看出,沿x方向的力矩(与Ff,y相关)和沿y方向力矩(与Ff,x相关)造成陀螺的晃动,这也是陀螺可翻转的原因。)

A.8问:这是一道定性问题,考查的是能量变化的物理图像。仅需要草图反映出总能量几个部分在各阶段定性地变化。这里给出能量变化的趋势描述,草图从略。

Etot:单调下降,从阶段Ⅰ某值单调降为阶段Ⅴ某一较低数值(此时只有势能)

Krot:单调下降,从阶段Ⅰ某值单调降为阶段Ⅴ～0

Ktrans:在阶段Ⅰ和阶段Ⅴ时～0;中间阶段略有上升。

Ug:阶段Ⅰ在某较低数值,随着Krot下降而上升,最终在阶段Ⅴ升至与Etot值。

A.9问:角动量在123系中的表达可由式(22)得到

比例系数k即为I1。

A.10问:由于摩擦力减少能量,外力矩减少角动量,很明显总能量与角动量不守恒。题目所问角动量沿某方向分量:L·υ 守恒,很明显要求这一方向(单位向量υ 所表示)上的力矩为0。从式(16)(或更直观地从力矩定义,力矩与力臂垂直),易知质心到接触点A 方向,即向量a方向上力矩必为0;所以

由于刚体|a|大小不变,所以下面可用L·a证明

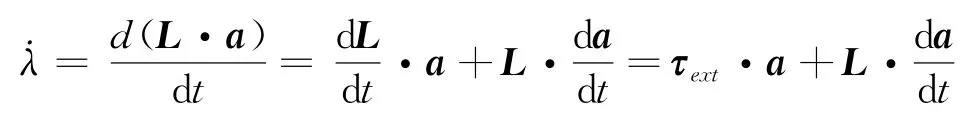
从式(16)可知τext·a=0。

从式(3)的a的表达式,并利用式(10)与式(25)可知

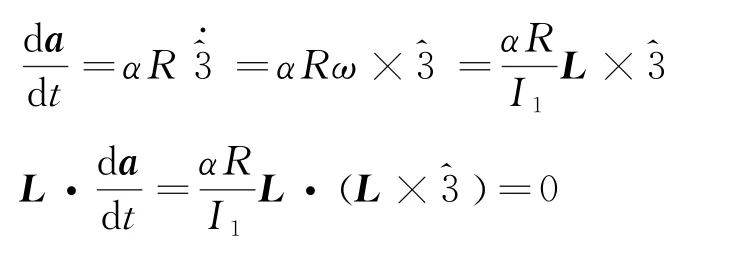
3 结语

刚体转动是力学以及分析力学中的典型问题,一般比较复杂。本题将一个经典的玩具模型简化,考查的正是处理这类转动问题的核心,即各个参考系中向量表达的变换关系。这是因为某些物理量,比如本题中的力臂向量a、角速度ω和角动量L,在某种特定表达下会比较简单;但建立力学运动方程或关系式时,用另一个参考系中的表达会更方便,这就用到了变换。而处理向量表达的变换时,最基本的就是参考系的基矢量之间的变换关系。从本题的解答中已充分体现了这点,选手的丢分大部分也是源于未搞明白变换关系。这部分在教学与竞赛培训中是值得强调与重点讲解的。