直线拟合的技术综合法及稳健性判据

郭旭波 肖志刚 朱美红 常 缨朱鹤年

(清华大学物理系,北京 100084)

误差分析和实验数据处理是物理实验的重要环节。在物理实验教学中,当已知两个物理量成较严格的直线关系时,常常先测量多组散布的实验数据,再通过拟合的方法求出直线斜率和截距的最佳估值。直线拟合有多种方法。常用的最小二乘法使残差平方和极小,计算简便,然而稳健性(抗粗差性)较差。最小一乘法使残差绝对值之和极小,但算法较复杂。本文在分析传统直线拟合方法的特点的基础上,提出了技术综合方法,并通过蒙特卡罗方法定量地比较了不同直线拟合方法的稳健性。

1 传统直线拟合法的特点分析

1.1 最小二乘法(least squares method,LSM)

勒让德与高斯创立的最小二乘法,使残差平方和(residual sum of squares,RSS)极小,LSM是统计学发展中的里程碑[1]。直线拟合常用LSM,对n个数据点(xi,yi)求出回归直线方程=b0+b1xi。LSM 的前提是高斯-马尔科夫假定:因变量yi具有独立、同分布的随机误差[2,3]。我们可用反证法粗略说明:测量多点散布数据作直线拟合,散布数据拟合主要目的是为减小因变量yi中随着自变量xi不同而具随机性的未定系统误差的影响[4],LSM 令极小而使稳健性(抗粗差性)变差,其中vi=yi-为残差。直线两端的数据点yi的误差ei对拟合斜率b1影响大,因为|∂b1/∂yi|∝|xi-，其中为xi的平均值。

1.2 最小一乘法(least absolute residuals method,LARM)

稳健性好,它以残差绝对值之和(sum of absolute residuals,SAR)极小为依据,SAR=由于LARM 算法较复杂,它的出现虽然比LSM 约早40年,但直到60年前进入计算机时代才开始被逐步推广[1]。

1.3 简化拟合法(simplified fitting method,SFM)

当n′为偶数且n′≤n时,用式由n个数据点(xi,yi)求斜率,是前计算机时代国外早已使用的简化拟合法[5]。当高度异常值点出现在直线线段端点附近时,由|∂b1/∂yi|≈const∝|xi-|0,可看出当异常点在直线两端时该法稳健性可能略优于LSM。

1.4 先剔除高度异常值后拟合的方法

先剔除高度异常值再回归是理想的稳健方法,但回归时的统计离群值判别是尚未系统解决的问题[6,7]。部分文献中,先用全部n组数据求出回归直线方程,用最大残差与其标准差之比G=作为离群值判断用的统计量。用G＞Gcr,0.99判据、剔除“粗差”后,常出现被剔除值的残差处于剩余(n-1)组数回归直线残差的“包含总体不少于99.9%、概率为99%的统计允许区间”内(依ISO 及GB 标准[8,9]),即sy,n-1,其中sy,n-1为剩余(n-1)组数回归的标准差,为包含总体不少于99.9%、概率为99%的统计允许区间因子。这说明此类判据往往有逻辑性瑕疵[4]。

1.5 经验调和法(empirical reconciliation method,EMM)

LSM 求斜率时有|∂b1/∂yi|∝|xi-|,SFM求斜率时有|∂b1/∂yi|=const,LARM 求斜率时可粗略地看作各个yi的贡献相近。我们曾提出经验调和法,力图调和上述方法的特点,对各yi乘以权重因子wi=|xi-+ε|-0.5,式中ε是小量。先以为新因变量,以和xi为自变量作“截距”为零的LSM 二元拟合求出b0和b1。再对拟合结果中大于的可能异常的值,降低一些权重，作第2轮加权拟合。

2 稳健拟合的技术综合法(technically hybrid method,THM)

对于理想模型为截距非零的、自由度不小于5的直线拟合问题,我们提出技术综合方法,力图部分综合上述几种方法的特点。THM 不作粗差剔除,仅在求斜率时适度降低ki=|yi-大于临界系数的个别数据yi的权重,以达如下效果:(1)稳健性显著优于LSM 及SFM,也优于LARM;(2)残差绝对值和、标准偏差近似与LARM相同;(3)计算过程比LARM 简单,适用范围广。

技术综合法的思路与步骤如下:

第1步,综合LSM 与SFM 的特点,用基于LSM 的加权拟合求斜率,使|∂b1/∂yi|近似正比于|xi-|0.5。

第3步,固定b1,在范围内用最小一乘判据求出截距b0来。

3 用蒙特卡罗法判断稳健性

用蒙特卡罗法定量地比较、判断不同方法的稳健性的步骤为:exp（1）+xiπ的点（xi,yit）。这里设xi等间隔,

(1)先构造n对误差为零、位于理想直线yit=xi=(2+n)i,i=1,2,…,n。xi在一定区间内呈均匀分布时也能得出与下文类似的结论。

(2) 蒙特卡罗法的参量选择。建立m组n-1个均值为0、总体标准差σ=0.01的正态分布(或均匀分布)的随机数组eij(j=1,2,…,m,m=2000),作为n个因变量中n-1 个yi的误差,yi=yit+eij。剩余一个因变量设置一个人为的“粗差”emax=±lσ,l=3,4,…,16。针对总体正态分布或均匀分布,n取7～16等不同点数,“粗差”点的位置原则上可分别取在直线上的不同位置。分别用LSM、LARM、THM、EMM 及SFM求出直线方程,计算下列特征参量:

回归预报值的最大误差的绝对值|eM|=这是拟合稳健性判断用的参量。

(3) 在l、n与“粗差”点位置相同时,用m组不同的误差分布数据分别计算标准偏差sy、残差绝对值均值与预报值最大误差绝对值|eM|,再作稳健性的统计分析。

4 用超限率二阶矩构建拟合稳健性的统计量

4.1 以均匀分布与高斯分布的卷积表征拟合预报值的误差极值分布

蒙特卡罗法拟合后的每组反预报值的最大误差为emi,其分布规律不再是正态分布,近似地假设其分布为相同标准差的均匀分布与高斯分布的卷积。设其概率密度为PR&G(em),且有可得99.0%,因此以±2.443σ作为反预报值emi的允许误差限±LPE,其绝对值LPE≈2.443σ作为|emi|的允许误差限。

当因变量个数n与l=|emax/σ|取某组值时,由蒙特卡罗法计算出回归预报值的最大误差绝对值eM。由于emax可能位于n个不同点位,一组条件下共有2000n个eM。

4.2 超限概率与超限率二阶矩

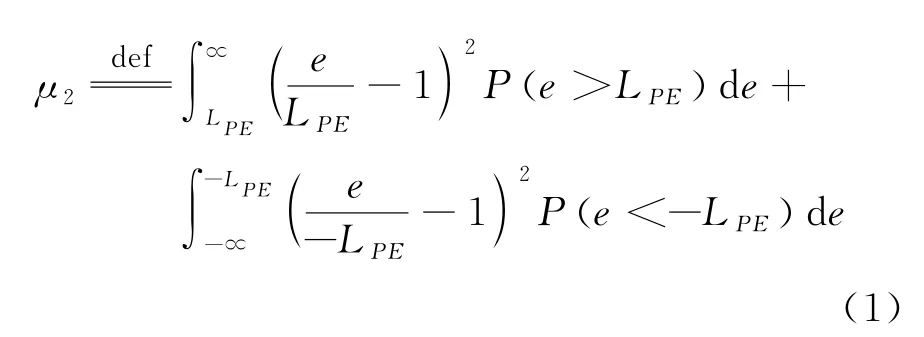
钱钟泰研究组提出了超限率二阶矩(over limited second moment)μ2的概念,其定义式为[4,9]超限率二阶矩μ2比超限概率pol能更全面地反映变量e超过误差限的程度[9],也具有可加性。随分布类型不同的超限率二阶矩μ2有较普遍的可靠性含义。对于分布函数双侧实际上被截尾的情形,μ2反映较多的可靠性信息。误差呈中心化正态分布时,文献[9]中给出显著性水平α=0.01对应的μ2,0.01=2.80×10-4。当emi的分布为相同标准差的均匀分布与高斯分布的卷积时,μ2,0.01≈2.17×10-4,记作。采用±作判断界限要比±μ2,0.01更苛刻些。

4.3 对α=0.01时emi 分布的误差限U0.99的讨论

对2000n个eM递减排序后,以第20n个数作为U0.99,p,以超限率二阶矩μ2≈2.17×10-4所对应的eM作为,然后取它们的方均根值分析10×14 组U0.99(n,l)的统计趋势,可以发现:

(2)U0.99能作为判断稳健性的参量之一,但不同n、l的U0.99(n,l)不具有可加性。如机械地对140组U0.99作平均,结果见表1。从表中可看出,THM 的最小。这与下文及的变化趋势稍有不同。

表1 5种直线拟合法的U0.99比较

续表

4.4 用超限率二阶矩构建稳健性新判据

对2000n个eM递减排序后,就能依次计算出与eM所对应的超限率二阶矩μ2。定出对应误差限LPE≈2.443σ的μ2,同时定出对应LPE的超限概率pol,它等于eM＞LPE的个数K与2000n之比。μ2等于超出允许误差限LPE的所有eM的超限率的平方和除以2000n,μ2的含义可以这样理解:如超限概率为1%,超限这部分eM的超限率约为

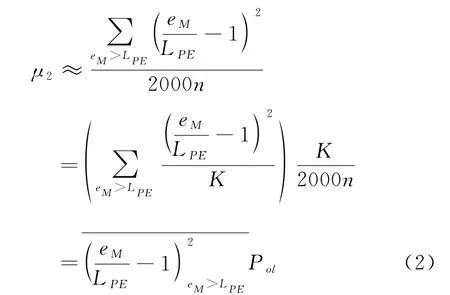
比较判断稳健性程度的统计量要便于对照比较,宜使量纲为1,并在不同参量下具有可加性。我们不用同一置信概率下以某种方法定义的误差分布的界限值U0.99,而用同一误差限时的分布特征量μ2。

n、l一定的条件下,当pol＜1%并且μ2＜2.17×10-4时,显然可认为eM的分布未见异常。对不同n、l的140 组数据汇总后作比较,计算pol＞1%或μ2＞时的总概率以及总超限率二阶矩,可以只用作为统计量,以判断不同拟合方法的稳健性程度。

4.5 用新判据比较5种拟合方法的稳健性

分别计算出5种拟合方法、140组n或l不同的pol和μ2之后,统计计算结果的及见表2。

不同方法统计量的比较以LARM 为对照,因LARM 是经典的稳健性方法。140组数据汇总结果表明:THM 的稳健性优于LARM,它们都显著优于LSM。SFM 的稳健性最差。表中EMM 的稳健性虽然看起来略优于THM,但是这是以高度统计离群值的大部分剔除为代价的。详细的计算表明:当离群值位于直线两端时THM 的稳健型优于EMM,THM 保留了LARM 的特征并优于后者。

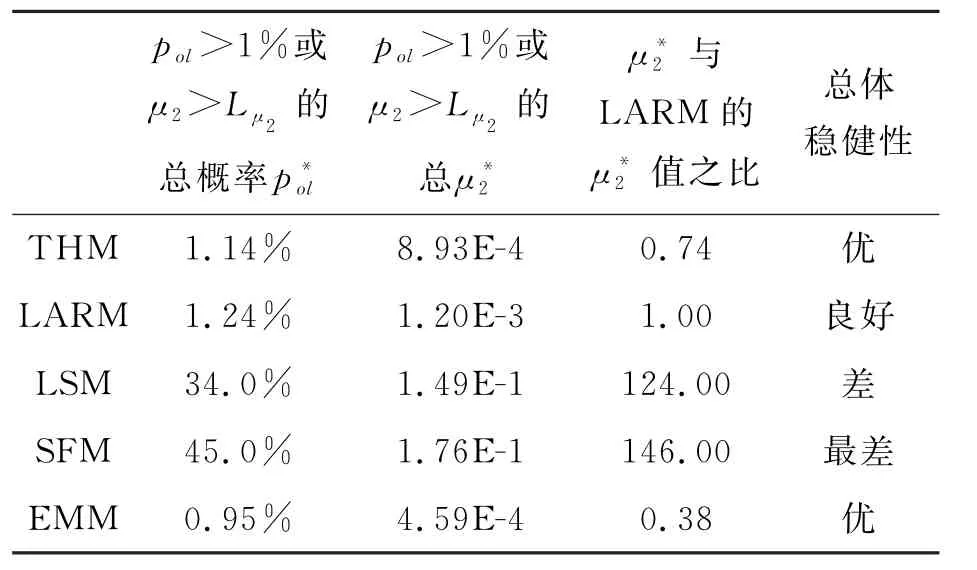
表2 5种拟合法、140组拟合的反预报值绝对值的统计量与稳健性比较

对5种方法、140组数的超限概率pol与超限率二阶矩μ2值作分析可知:当μ2＞2.17×10-4且pol＞1%时,EMM 只有n=7、l=3 这一组数的μ2明显大于LSM 的μ2;THM 也只有当n=7、l=3或4这两组数的μ2明显大于LSM 的μ2,说明当l＜5时LSM 也有一定的稳健性。EMM所有组的μ2均小于LARM 的μ2;THM 只有当n=9或10、l=5这两组数的μ2大于LARM 的μ2的（1+1/6）倍,说明EMM 与THM 的稳健性优于LARM。

EMM 与THM 的稳健性优于LARM,因为前两种方法不同程度地降低了粗差l=|emax/σ|较大的单个数据的权重,l很大时使用EMM 拟合相当于剔除了高度离群值,THM 在求斜率时也相当于剔除了高度离群值,只在求截距时用到该值。当已知两变量呈严格直线关系时,宜用EMM作稳健回归;而当变量直线关系的严格性未知时,宜用THM 稳健回归。

固定l时,总超限率二阶矩随n的增加大致呈递减关系。固定n时随l变化的趋势见表3。图1是随l的增加而变化的曲线。图中LSM 与LARM 的曲线单调递增。EMM、THM 与LARM 的曲线大部分在临界值水平线lg(2.17E4)上方,自下而上依次排列。

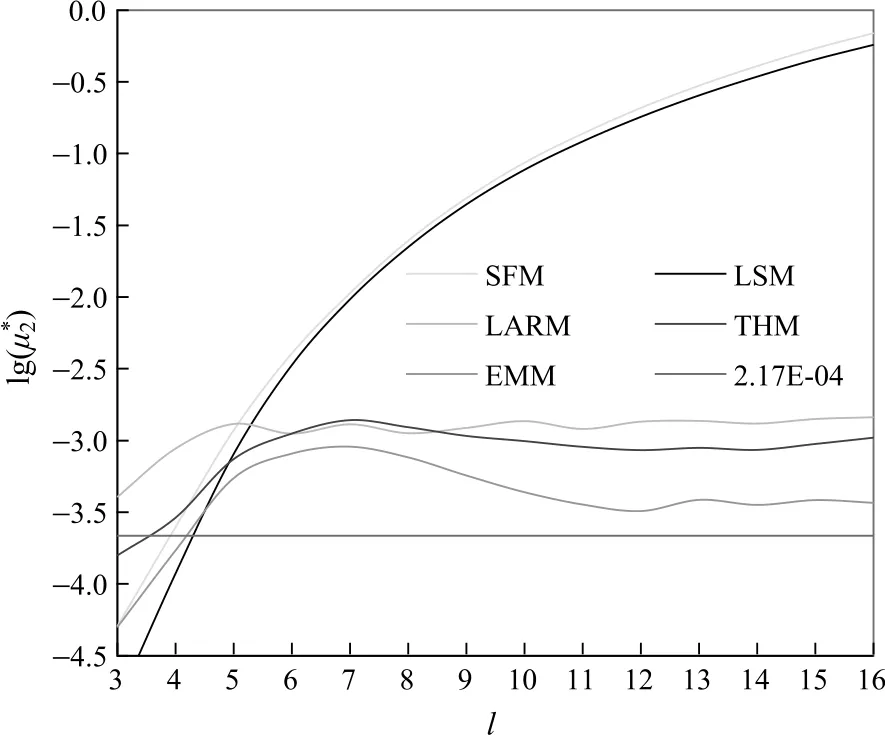
图1 随l增加而变化

求5种方法的准偏差sy、平均绝对残差分别与LARM 的相应量之比,比值的平均值见表4。

表3 固定n 时的 随l变化数表

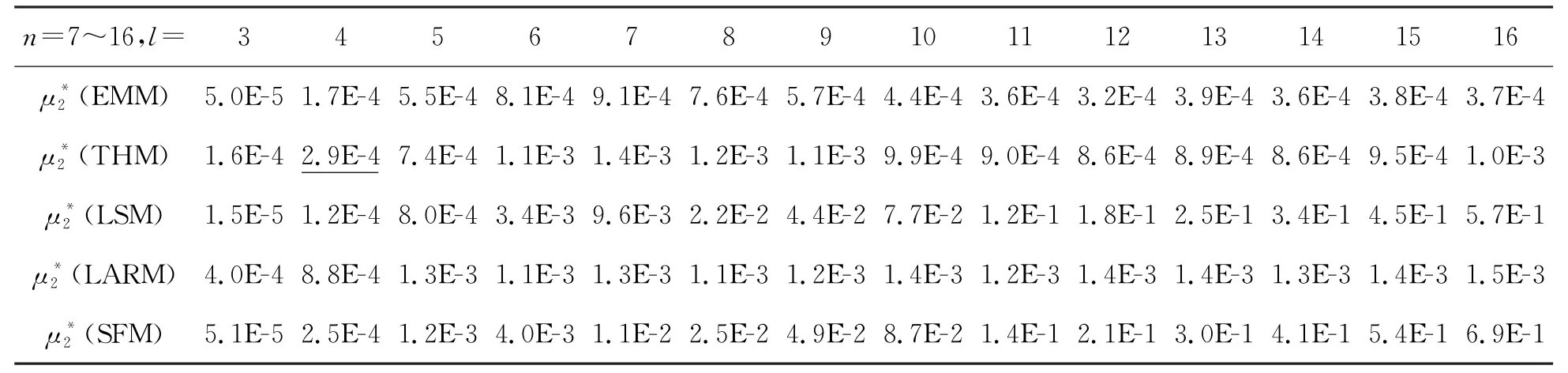
表3 固定n 时的 随l变化数表

表4 5种方法的准偏差sy、平均绝对残差分别与LARM 的相应量之比

表4 5种方法的准偏差sy、平均绝对残差分别与LARM 的相应量之比

标准差sy是LSM 极小,THM 与LARM 两种方法sy的均值之差约0.22%;平均绝对残差是LARM 极小。LARM 与THM 两种方法的均值之差约1.8%。可见THM 的这两个评价参量与LARM 相差甚小。THM 保留了LARM 的经典统计的主要特征及优点。EMM 的sy及的均值分别位于LSM 与LARM 的相应量值之间。

5 技术综合法在实验教学中的应用案例

表5 色散曲线7波长直线拟合时不同方法的稳健性比较

从表5的最后一行可以看出,即使某一角度错读了30′,用稳健性好的技术综合法拟合,在测量范围内仍然可得出高置信概率的合理色散曲线,使预报值ni的误差不大于U0.99。从表5也可看出:虽然THM 的残差特征值比LARM 大4%或2.4%,但误差特征值反映的抗“粗差”性较显著地优于LARM,更是大大优于LSM。

6 结语

本文对直线拟合的技术综合法的思路和步骤进行了介绍。技术综合法不作粗差剔除,仅在求斜率时适度降低大于临界系数的个别数据的权重,且计算过程比最小一乘法简单,适用范围广。用蒙特卡罗法对不同直线拟合方法的稳健性定量比较的结果表明,技术综合法的稳健性显著优于最小二乘法,也优于最小一乘法;残差绝对值和、标准偏差近似与最小一乘法相同。实验教学应用案例表明,在测三等角棱镜材料的色散曲线数据时,即使某一角度有较大粗差,用稳健性好的技术综合法拟合仍然可得出高置信概率的合理色散曲线。