二维曲面理论引入数学物理方法的探讨

陈起辉 黄飞杰 傅永平 祝凤荣

(1 西南交通大学物理科学与技术学院,四川 成都 610031;2昆明学院物理系,云南 昆明 650214;3滇西科技师范学院物理系,云南 临沧 677000)

纵观物理学的发展史,我们会发现物理学的发展常常以相应的数学的发展为先导,而在这之中几何学无疑对物理理论的建立起到至关重要的作用。例如牛顿力学是建立在欧几里得(Euclid)几何所描述的平直时空之中,而广义相对论的数学基础是描述弯曲时空的黎曼(Riemann)几何。然而在实际的教学中,物理本科生在从狭义相对论过渡到广义相对的学习过程通常会遇到非常大的障碍,其主要原因是对黎曼几何知识的缺乏。尽管在有些广义相对论教材中会补充相应的黎曼几何的初步数学知识[1],但是对于没有任何内蕴几何知识背景的学生而言,一开始就学习高维空间(至少四维时空)中的几何知识,未免过于抽象,学生往往并不能对这些抽象的代数运算有任何直觉上的把握。幸运的是,从黎曼几何发展的历史看[2],它是将高斯的二维曲面理论向高维空间的拓展。因为二维曲面可以嵌入到我们熟悉的三维空间中,对其我们有非常直观的印象,并且本科生在高等数学和大学物理中,已经接触了部分曲线、曲面积分、平面曲线曲率,矢量积分的知识,所以基于这些知识,我们可以建立相当直观的二维曲面上的内蕴几何知识[3]。这无疑将为学生学习更高阶的微分几何知识提供必要的基础。当今前沿物理学中对规范场,拓扑场论,陈拓扑绝缘体,拓扑超导体等的广泛研究,急需理论物理的学生具有扎实的微分几何知识。

数学物理方法作为为本科生的后续理论物理课程提供相应数学方法的一门课,可以在课程设置中包括相应的微分几何知识。这对于物理专业的本科生是非常必要。然而从目前所存在数学物理方法的教材来看,几乎都没有涉及曲面上微分几何的知识。其主要原因在于:①微分几何知识体系极其庞大且抽象,不可能在数学物理方法的有限章节中涉及这些知识的方方面面;②几何知识相对于传统数学物理方法内容相对独立,难以与原有知识体系有机的融合;③就目前数学物理方法所包含的内容要在规定的学时内讲完已经存在一些困难,更不用说再增加新的内容。针对上面的3个问题,所以我们在本文中探讨如何将二维曲面理论引入到数学物理方法的教学中,并在此基础上做相应的延伸。

对于上面的第一个问题,我们旨在为本科生进一步学习抽象的微分几何知识提供直观的基础,所以只介绍曲面理论中第一,二基本形式以及线元、面元、曲率、平行移动等概念。借助将二维曲面嵌入到三维空间的参数方程,学生比较容易建立起这些概念,并可把这些概念推广到高维的黎曼几何。对于第二个问题,我们基于曲面理论,讨论曲面上的梯度、散度及旋度的形式,这部分内容可以运用于数理方程的建立及正交曲线坐标系中的拉普拉斯方程求解,从而与数理方程部分的内容有机融合。对于第三个问题的解决,视具体情况,对于某些专业,数学物理方法有足够的课时,所以包括这部分内容不存在问题。而对于要求相对较低的专业,这部分内容可以作为带星号的内容,为选讲或者留作学生自学拓展内容。另一方面,目前的线上线下混合教学模式,因为线上录播视频可以节约大量教学时间,并且便于学生反复观看。可以将这部分内容考虑作为线上课程,提供给学生自学。

下面我们在技术层面讨论如何在数学物理方法中引入曲面理论,以及给出其在皂膜上的流体力学上的应用。最后,也对如何推广到高维黎曼几何并应用于广义相对论做一个简要的介绍。

1 三维空间中的曲面方程

图1 二维平面区域映射到三维曲面

2 曲面上的度规——第一基本形式

利用dr可以得到曲面上线元的长度表达式,因为dr=rudu+rvdv,所以有

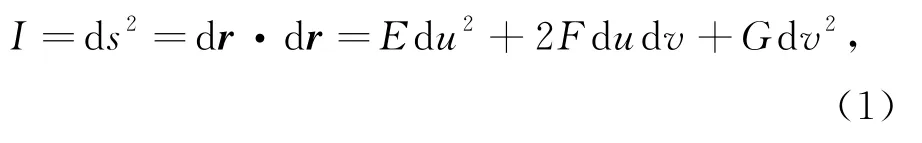
其中E=ru·ru,F=ru·rv,G=rv·rv,这便是高斯引入的曲面第一基本形式。通常也记为ds2=gijdxidxj,i,j=1,2,该式运用了爱因斯坦求和约定,重复指标意味求和,并且我们定义了x1=u,x2=v,在后面的讨论中我们将在不同的情形中混合使用这两种表示方法。定义称为度规张量矩阵,因为长度的平方必须大于零,所以度规张量矩阵必须是正定的。然后曲面上的面元与两条曲线的夹角(定义为曲线交点处切线的夹角,如图2所示)的余弦,用度规张量分别表示成为,

如图2所示,这两条曲线的参数方程是以线元为参数,记为:(u(s),v(s)),(u′(s′),v′(s′))

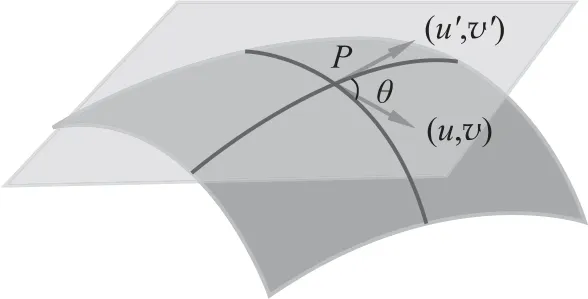
图2 曲面上相交曲线间夹角

可以证明以上的线元、面积元、曲线的夹角在坐标变换下,形式是不变的。有了这些量,我们便可以像在平面几何上一样,在曲面上利用度规张量通过积分研究长度、面积以及角度之间的关系。对曲面的描述还需另外一个重要参数——曲率,下面我们就来介绍它。

3 曲面的曲率——第二基本形式

同样,利用位置矢量r可以引进曲面的曲率以及测地线概念。如图3所示,设曲面在r(u0,v0)点的切平面为Σ。我们考虑在(u,v)偏离(u0,v0)时,r(u,v)偏离切平面的情况。因此我们计算

上式右端第一项是线性项,位于切平面内;在法线方向的偏离是在第二项中的二阶量,所以定义r在法线方向的偏离为

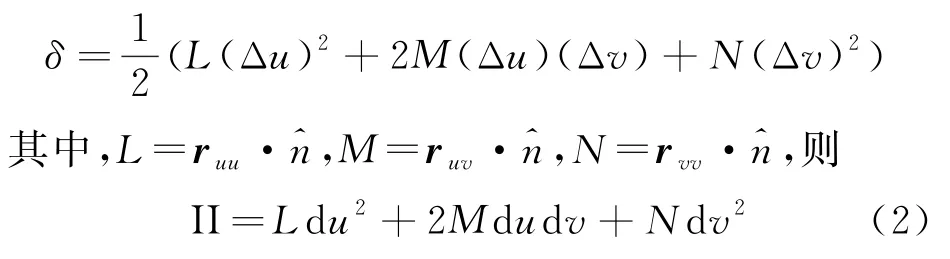
称为曲面第二基本形式。可以证明该表达式在坐标变换下也是不变的,其中系数的矩阵形式为。位置矢量的二阶导数rij在切平面中的分量,定义了另一个重要的量,克里斯托弗符号,它表示的是rij在切平面中的分量在rk方向上分量的展开系数。值得指出的是,如果我们引入曲面第一基本形式系数矩阵gij的逆矩阵为gij,即,则克里斯托弗符号完全由曲面第一基本形式给出为

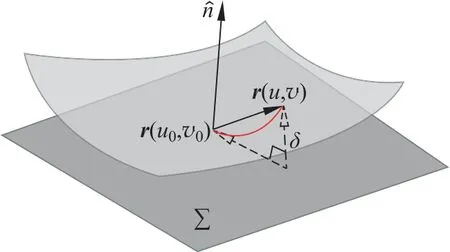
图3 曲面对切平面的法向偏离量δ

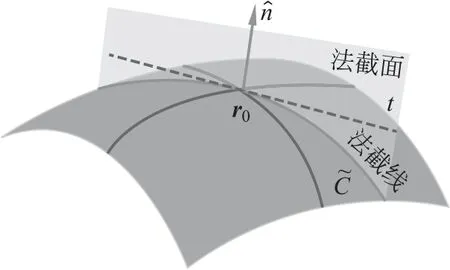
图4 法截面与法截线

若用弧长s为参量的参数方程为r(u(s),v(s)),则根据定义曲线在切点处的曲率为

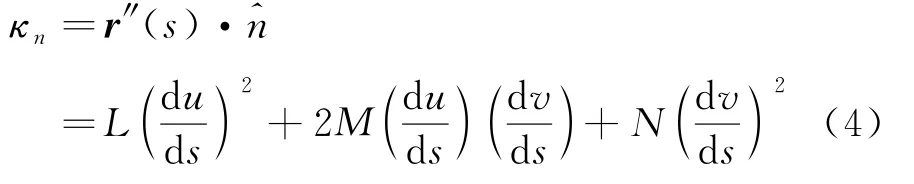
以上表达式只需要运用微分链式规则求导运算即可得到,所以该曲率完全决定于第二基本形式。现在来计算κn对主截面方位的依赖关系。如图5所示,不失一般性,可以假设在切点处ru⊥rv,因此F=0。设切点处曲线～C的切线t与ru的夹角为θ,即dr与ru的夹角。利用dr=rudu+rvdv,可以推出

为a1,a2。设dr与a1夹角为φ,则可以得到κn（φ）=κ1cos2φ+κ2sin2φ,利用κ1,κ2可以定义两个新的量

图5 at、a1和a2分别表示法截线、主曲率(κ1,κ2)在切平面中所对应的方向

从法曲率κn(φ)表达式可以看出曲线在切点处的曲率完全由κ1,κ2及曲线切线与a1的夹角φ所决定。如果忽略人为选择φ的影响,我们可以说曲面在切点处的弯曲性质由κ1,κ2完全决定。

人们运用高斯曲率来刻画曲面的弯曲特征,①当κ1,κ2同号则K大于零,则沿任意方向的法曲率κn(φ)与κ1,κ2同号,这时法截线朝着一个方向弯曲,对应的切点叫做杯点或者椭圆点,如图6(a)所示。②如果κ1,κ2中有一个为零,则对应的切点叫做抛物点,如图6(b)所示。③当κ1,κ2异号则K小于零,对应的切点叫做鞍点或者双曲点,如图6(c)所示。

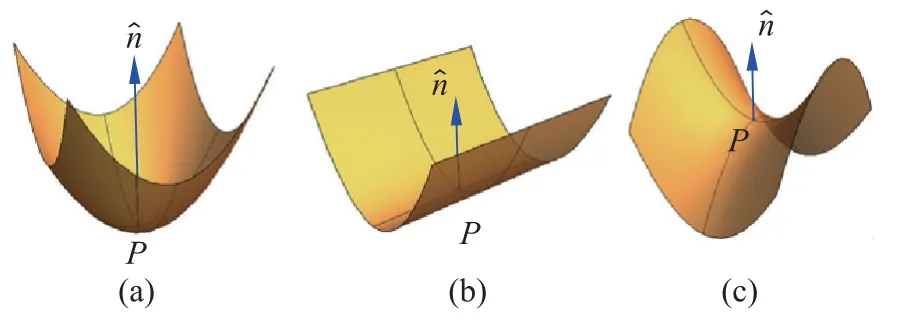
图6 三维空间中的弯曲程度

历史上,高斯作出了一个重要观察:曲面的高斯曲率完全由曲面上的度规给出(即第一基本形式)。这初看起来似乎难以想象,因为高斯曲率反映的是曲面在三维空间中的弯曲程度。事实上如果我们仔细考查就会发现并不完全是这样,高斯曲率刻画的只是曲面的内蕴性质。从式(6)我们知道高斯曲率是由两个本征曲率κ1,κ2的乘积给出,所以高斯曲率为零,并不能得出曲面在三维空间是没有弯曲的,例如圆柱面的高斯曲率为零,但是在三维空间它在一个方向上有弯曲(参考图6(b))。同样可以证明,对于圆柱面的平均曲率不为零,平均曲率不是曲面的内蕴性质。具体说来,如果在曲面上选择的是正交坐标网F=0,则高斯曲率可以由第一基本形式表示成下式,

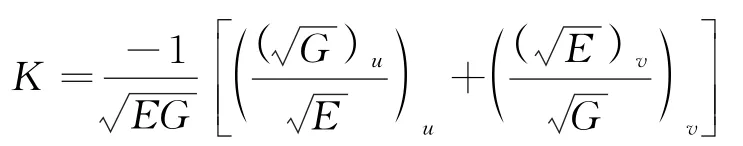
高斯得意的称这个定理为绝妙的定理(Theorema Egregium)。

4 测地线

考虑在曲面上的一条曲线,其以弧长为参数的方程为γ(s)=r(u(s),v(s)),求二次导得到

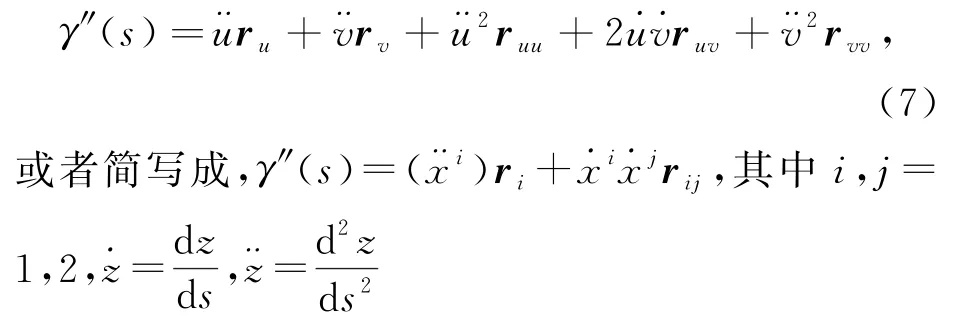
利用式(3)定义的第二基本形式以及克里斯托弗符号,式(7)可以进一步写成

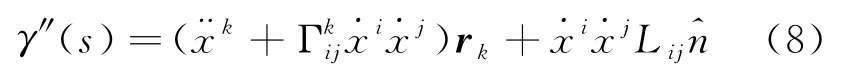
很容易看出,第一项表示曲线方程二阶导数的切向分量,记为:,其数值大小给出测地曲率κg,它刻画了曲线在曲面上自身的弯曲程度。第二项是法向分量,记为,等于γ″·,它刻画的是曲线由于曲面的弯曲而产生的弯曲。这两个曲率的不同,可以通过图7清楚地看出。

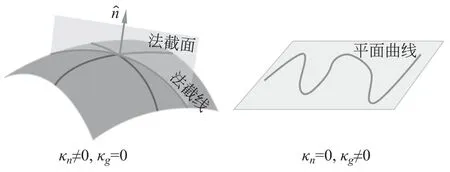
图7 左图(右图)法曲率不为零(为零),测地线曲率为零(不为零)

我们进一步来讨论测地线曲率。因为曲线是以弧长为参数,所以γ′·γ′=1,对其两边同时微分可得γ″·γ′=0,即·γ′=0,又因为·γ′=0,所以·γ′=0。这说明同时与和相互垂直(如图8 所示),因此有如果对于一条曲线,它每一点处的测地曲率都为零κg=0,这样的曲线叫做测地线。根据式(8),可以得到测地线所满足的微分方程为

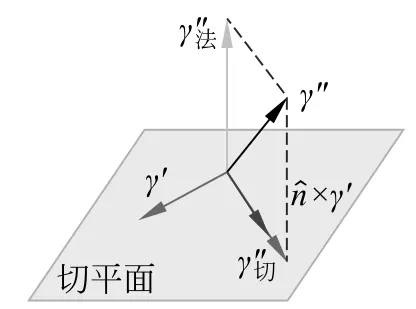
图8 曲线γ(s)的一阶、二阶导数在切平面与法线上的投影

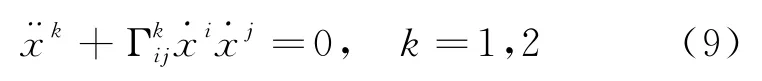
这是两个二阶的微分方程,通过求解方程,即可求出曲面上任意两点间的测地线。例如在平面上的直角坐标系中,因为=0,所以很容易求出其测地线为直线。

测地线的另一个等价定义是曲面上两点间的短程线,即在适当小的范围内联结任意两点间的曲线中,测地线是最短的。可以利用曲面的第一基本形式中的线元公式通过变分来证明,所以测地线可以理解为在曲面上的直线[4]。

5 曲面上矢量的平行移动

在高维的弯曲空间中矢量的平移是一个非常重要同时又非常抽象的概念。然而这个概念在二维曲面上,我们可以得到一些直观上的把握。首先,曲面上的矢量指的是定义在切平面中的矢量。其次,从一点到另外一点的平行移动不是通常三维平直空间中的平移,因为这样平移后的矢量通常不在曲面的切平面内,因此需要重新建立平行移动的概念。

如图9所示,考虑曲面上的沿着曲线C上的矢量场,它由参数方程a(t)=a1(t)r1(t)+a2(t)r2(t)给出。假设我们知道它在P点的矢量为a,在它邻近一点P′处的矢量为a′=a+da,若将其按照通常意义下的空间平移移动到P点,则a′一般不在P点的切平面内。如图9所示,将其分解为沿着切平面的部分和垂直于切平面的部分。垂直切平面的部分可以表示成,因为a是在切平面内,所以·a=0,所以沿着法线的分量为。从a+da中减去垂直切平面的分量,得到其在切平面的分量,记为(a+da)t,即(a+da)t=a+da-。然后我们把在P点(a+da)t与a的差叫做矢量场a(t)从P点沿曲线C移动到点P′的绝对微分(也叫协变微分),用Da来表示

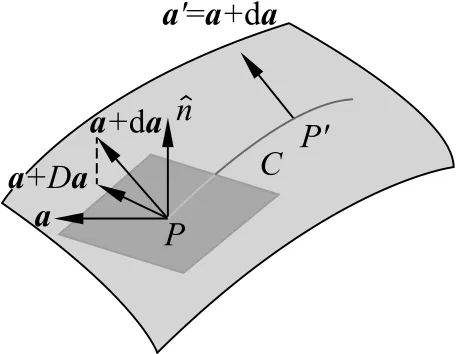
图9 曲面上矢量沿一曲线的平行移动示意图

可以看出Da仍然是P点处切平面中的矢量。

当Da=0时,表示矢量a从点P沿C的方向移动到点P′时,微分da沿法线的方向,或者说,把矢量a+da投影到点P的切平面时,我们得到矢量a,这时称矢量a+da是矢量a从点P沿C方向经过平行移动到P′点。这样定义的平行移动,也叫做列维-奇维塔(Levi-Civita)平行移动,它依赖于连接P,P′的曲线。如果所考虑的曲面是平面,列维-奇维塔平行移动将回到我们所熟悉的平行移动。

利用定义式(10)也很容易推导出绝对微分的解析式,根据a(t)的表达式有

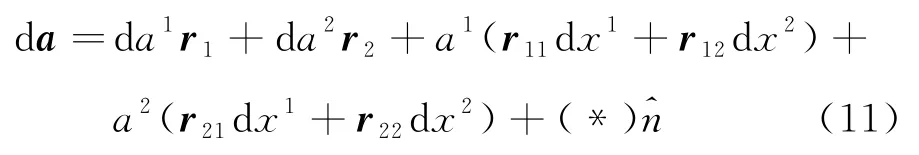
如果考虑a沿着某一已知曲线xi=xi(t)作有限的平移,可以得到a分量所满足的微分方程为。这是一个关于ai的线性方程组,由微分方程的理论知道,方程的解是存在且唯一的,因此矢量沿已知曲面上一条曲线做平行移动总是可以唯一的实现。

6 二维曲面理论的应用

梯度、散度、旋度是刻画矢量场性质的三个重要物理量。人们也很容易从它们的定义看出物理意义,在大多的教材中给出了在三维直角坐标系中如何通过定义来得到它们的微分表达式[5]。然而如何根据定义推导在曲线坐标系乃至弯曲空间中的表达式,据我们所知,还没有看到这样的推导。在下面我们将推导这些算符在曲面上的表达式,这些表达式能够很自然的推广到高维。最后再将讨论如何将这些理论运用到肥皂膜上的流体力学。

7 二维曲面上梯度、散度、旋度公式

梯度:在三维正交坐标系中,我们知道标量函数f(x,y,z)沿着以弧长为参数的曲线C:{x(s),y(s),z(s)}的方向导数可以表示成

考虑到对于标量函数的协变微分与偏微分是等价的[4],上式也可以表达成

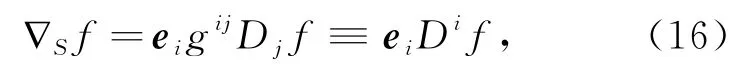
其中Di≡gijDj。(16)式是梯度算符适用所有维度的一般表达式。

散度:回忆电磁学及流体力学中的知识,三维空间中散度的定义为[6],即它等于在矢量场f(x,y,z)中穿出某一无限小体积元表面的通量与该体积元的比值。如果该比值不等于零,则说明该体积元所在点存在“源”(对于电场,源就是产生电场的电荷;对于流体,源就是流体产生或消失的地方)。

对于二维曲面,考虑定义在曲面上的某一足够光滑的矢量场,A(u,v)=Aueu+Avev。类似于三维空间,曲面上的散度定义为

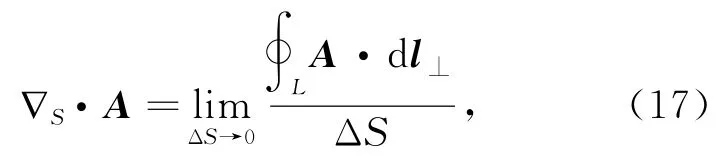
即它等于在矢量场A(u,v)中穿过某一无限小曲面边界的“通量”与该面积元的比值。注意dl⊥表示垂直边界且指向面积外部的矢量线元。从该定义同样可以清楚的看出二维曲面上散度的物理意义。

现在来推导∇S·A的具体表达式。为此,如图10所示在曲面上作一个由坐标线围成的面积元(可看作四边形),所以穿过四边形微元边界的通量可以分别在四个边上给出为

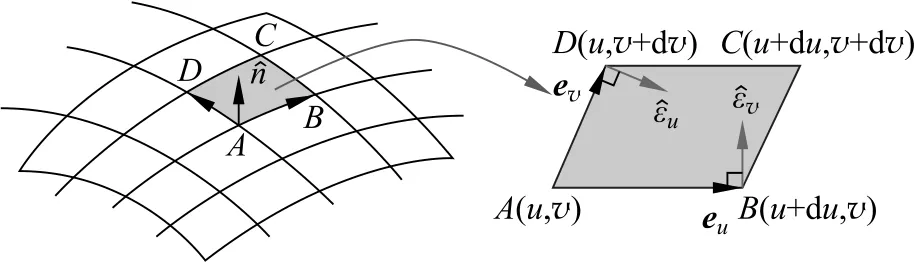
图10 由坐标线所围成的无穷小面元ABCD(阴影区域)

根据前面我们对各量的定义,结合AB与CD上的通量得到

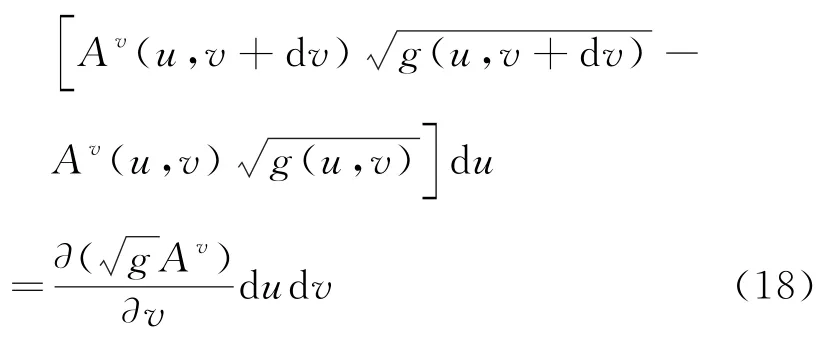
结合BC与AD上的通量得到

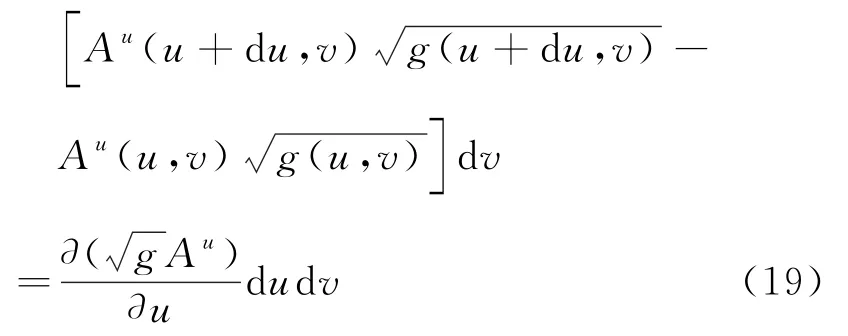
结合式(18)与式(19)并利用面元的定义得到穿个整个边界的通量为

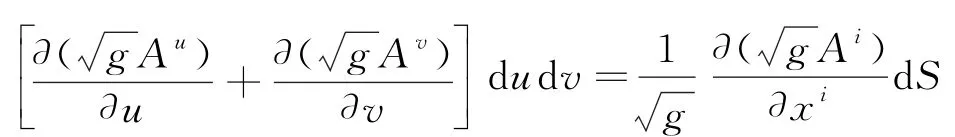
对比散度的定义式(17),得到在二维曲面上矢量场的散度为

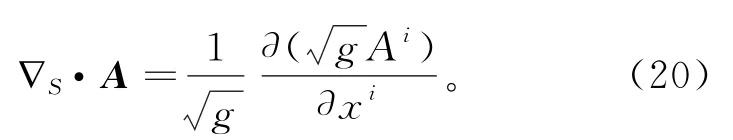
结合我们的讨论并运用和三维情况类似的论证方法[5],可以得到在曲面上的高斯公式为

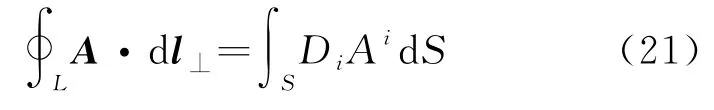
同样这个式子对于高维情况也是成立的,并且可以证明该表达式用协变导数表达出来为∇S·A=DiAi,可以参考文献[4]。值得注意的是此表达式和三维平直空间的情况完全类似,只需把协变导数变成偏导数即可。

旋度:与三维情况类比,曲面上的旋度定义为,,dl‖是沿着边界L切线方向的矢量线元。矢量场A(u,v)在某一点沿着垂直该点切平面方向的旋度为,沿着围绕该点的无穷小边界矢量场的环量与该边界所包围的面积的比值。旋度在有些教材上也被形象地叫做涡度,因为从上面的定义式容易看出,如果流体中存在旋涡,则围绕旋涡中心的旋量不为零,即在旋涡中心处旋度不为零。所以旋度是刻画流体中存在旋涡的强弱的物理量。

与散度的推导类似,如图10所示同样选择一个由坐标线围成的无穷小面积元,分别计算在四边形每个一个边上对环量的贡献

CD上的旋量:-A(u,v+dv)·eu(u,v+dv)du

AB上的旋量:A(u,v)·eudu

BC上的旋量:A(u+du,v)·ev(u+du,v)dv

AD上的旋量:-A(u,v)·ev(u,v)dv

后一个等式利用了联络在作差后会消失的性质,所以可用协变导数代替偏导数。同样,对应的也有曲面上的斯托克斯公式为

拉普拉斯方程:在三维直角坐标系中,拉普拉斯方程定义为∇·(∇φ)=0。方程左边表示对标量函数φ取梯度得到矢量函数后再取其散度,对于二维曲面也是同样的定义,代入在前面得到的梯度和散度表达式可以得到此时的拉普拉斯方程形式为

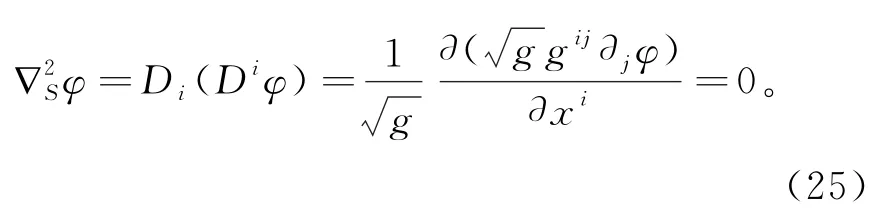
最后需要指明的是,利用上面得到的梯度、旋度、散度公式可以推出在正交曲线坐标下的梯度、散度及旋度的表达式。以球坐标为例,其度规张量为grr=1,gθθ=r2,gφφ=r2(sinφ)2,其他矩阵元为零。在代入公式时需要注意的有两点:首先,把前面得到的公式推广到三维,即求和指标换作i=1,2,3。其次,在通常的球坐标系中矢量场展开的基通常是单位矢量,应该将其变换到自然标架的基上,即,所以,代入公式的各分量分别是Ar,

8 二维曲面理论的应用——肥皂膜上的流体力学

相信几乎每个人的童年都玩过肥皂泡,然而小小的肥皂泡却包含了丰富的物理。人们对肥皂膜的研究可以追溯到牛顿时代。在阳光下,仔细观察一个肥皂泡的表面,可以看到许多彩色条纹。这些彩色条纹是由于薄膜干涉产生的,属于等厚干涉现象。如果多观察一段时间,可以看到这些条纹在不停地变化着。这说明肥皂膜的厚度时刻在发生变化,或者说肥皂膜中的液体时时处于流动的状态。导致皂膜上液体流动的外部驱动力,一部分来自于重力,一部分来自于空气流动所造成的力。这些外部力与皂膜内部的表面张力以及粘滞力一起决定了皂膜上的液体流动。又因为皂膜非常的薄,所以皂膜上的流体也可以看作二维曲面上的流体。对二维流体的研究已经存在着非常多的文献[7,8,9,10]。本文主要介绍如何将曲面理论与流体力学相结合,运用到固定曲面上的二维流体(即,曲面不随时间发生变化),得到控制流体演化的方程。

采用文献[7]中谢锡麟等人的观点,在皂膜上一点处的液体面密度表示成为ρ=hρV,其中ρV表示液体的体密度(假设为常数),h表示皂膜的厚度。因此,如果知道皂膜的面密度ρ(u,v,t),便能从理论上预言其上的条纹分布。假设在皂膜上的速度分布为V(u,v,t),根据质量守恒可以得到连续性方程为

其中S为皂膜上任意选择的一个面积,L是S的边界。因此上式的物理意义是,S中单位时间内面密度的增量,等于单位时间内流入到S中的质量。利用前面得到的在曲面上的高斯定理可以得到连续性方程的微分表达式为

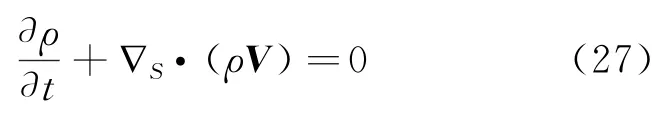
然后,将牛顿第二定律运用到皂膜上的某一个面积微元上,采用和前面曲面上梯度定义类似的讨论,可得到微元的动量改变为

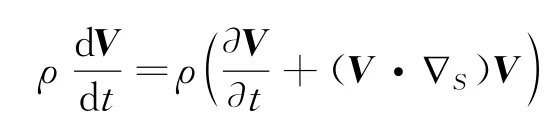
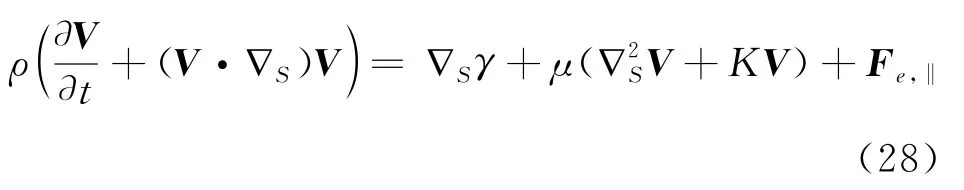
在上面的矢量方程中只取了与曲面相切的分量,因为其垂直分量只提供保持曲面不变的平衡力,不改变切速度的大小。另一点值得注意的是,在曲面上,高斯曲率结合曲面上的流速场一起产生等效的力,参与动量的平衡。

从上面的讨论可以看到描述固定曲面上流体状态需要四个量,速度V的两个分量,以及表面张力γ和流体面密度ρ两个热力学量。因此,完整的流体力学方程组应该包括四个方程。方程(27-28)式提供了三个方程,分别是连续性方程与纳维-斯托克斯方程。第四个方程是曲面保持不变的平衡方程[10]。

9 黎曼几何及广义相对论简介

黎曼几何:受高斯的影响,黎曼进一步思考对于物理空间究竟什么是最本质的。黎曼认为我们只能局部地了解周围的空间。这一点不像前面讨论二维曲面时的情形,在那里我们可以把它嵌入到三维空间中观察它形状的变化。我们却很难想象在四维空间中嵌入三维曲面,来研究三维空间的弯曲,我们能够确定的是在三维空间中两个相邻点间的距离。因此黎曼在题为《几何学基础所依据的假设》中将高斯的曲面理论推广到n维流形[13,14]。

假如流形上每个点的坐标记为（x1,x2,…xn）,线元为,ds2=gij(x)dxidxj,正如前面所讨论的,流形上的几何量(如线元,面元,夹角,高斯曲率)都可以由gij给出。在黎曼看来,我们不需要第二基本形式,因为它不是空间的内蕴性质。

黎曼的另一个重要贡献是将二维高斯曲率推广到n维情况,他引入了黎曼曲率张量

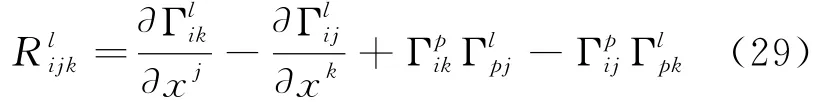
我们很难从黎曼曲率张量的定义式(29)直接看出其几何意义。粗略的来说,黎曼曲率张量刻画的是将一矢量沿着曲面上某一无穷小闭合路径平行移动,回到原来位置时它与原矢量的差别程度[15]。如果是在平坦的空间上,这个差别为零。二维曲面中的高斯曲率也可以用黎曼曲率张量和度规张量表示成,或者从这个式子也可看出高斯曲率完全由度规张量给出,是曲面的内蕴性质。黎曼几何可以看作是二维曲面理论的直接推广,在二维曲面论中成立的公式,在n维流形的情况也同样成立,只需把原来求和指标由i=1,2变为i=1,2…n即可。

广义相对:不同于牛顿的绝对时空观,在狭义相对论中,时间与空间统一为四维时空,不同惯性系的时空坐标满足洛伦兹变换。而洛伦兹变换的要求等价于闵可夫斯基(Minkowski)四维时空间隔ds2=(cdt)2-(dx)2-(dy)2-(dz)2=ημνdxηdxν在洛伦兹变换下是不变的。其中c为光速,μ,ν=0,1,2,3,(x0,x1,x2,x3)=(ct,x,y,z),ημ,ν=diag(1,-1,-1,-1)是4×4的对角矩阵,叫做闵可夫斯基度规。

与曲面理论作对比,可以发现对狭义相对论的研究事实上归结为对四维闵可夫斯基空间几何的研究。需要注意的是,和普通的四维欧几里得空间不同,时空间隔可以小于零,所以度规张量矩阵不是正定的,因此四维闵可夫斯基空间也叫伪欧几里得空间,它具有最大的对称性。当考虑引力时,由爱因斯坦等效原理知,引力场要对时空属性产生影响,四维时空将会产生弯曲,此时描述时空性质的几何将是黎曼几何。

在广义相对论中,时空间隔一般可以成为ds2=gμνdxμdxν,其中度规张量gμν是时空坐标的函数。时空的几何特性都蕴涵在度规张量中,它是由时空中的物质能量分布所决定。爱因斯坦场方程便是告诉我们如何通过空间的物质能量分布来确定时空的度规张量。

与曲面理论中完全类似,通过度规张量gμν可以构造联络,利用联络又可以得到黎曼曲率张量。它们具有与曲面理论中相同的形式,只是各指标取值变成从0到3。爱因斯坦场方程由下式给出

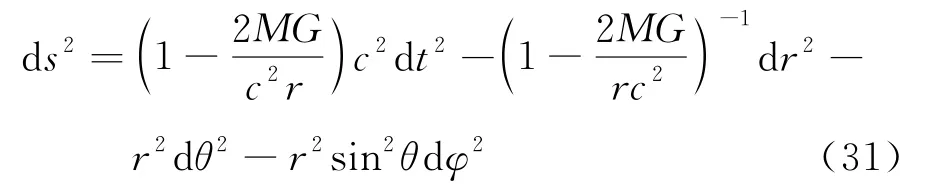
10 结语

我们介绍了二维曲面理论中的第一、二基本形式,曲率,测地线,平行移动的概念,利用这些概念推导了曲面上的梯度、散度、旋度公式。这些公式很容易推广到高维情况,可以应用到数理方程的建立与求解中。我们也讨论了如何将曲面理论应用到曲面上二维流体,得到控制流体运动的连续性方程和维纳-斯托克斯公式。然后我们介绍了将曲面理论推广到高维中的黎曼内蕴几何,以及其在广义相对论中的应用。通过这些内容的介绍,我们旨在探讨如何在数学物理方法中引入曲面理论的知识,为本科生打下学习更高阶微分几何知识的基础。当然正如我们前面叙述的,微分几何的知识体系非常的庞杂,作为数学物理方法的一部分内容,不可能涉及所有方面。我们尽量选择作为微分几何入门中常遇到的困难概念来展开讨论,建立它们在曲面上的直观图像,从而为理解更加抽象的概念提供基础。