再谈拉格朗日函数非唯一性的物理意义:广义规范变换和正则变换的等价性证明

韦联福

(1 东华大学理学院,上海 200269;2西南交通大学信息科学与技术学院,四川 成都 610031)

经典分析力学中的一个熟知结论是,力学系统的拉格朗日函数是非唯一确定的:即相差任意一个广义坐标和时间全微分项的两个拉格朗日函数是等价的,他们导致一个共同的拉格朗日运动方程。所以,一般认为这个全微分项对动力学问题的研究是没有什么物理意义的,在大多数教材都只是简单地提及这一特性,而对其蕴含的物理意义也就不多加以阐述,从而在实际教学中留下不少误解和争议。实际上,正如文献[1,2]所指出的那样,拉氏函数的不确定性实际上是动力学方程规范不变性的一种表现,这种规范变换可看作哈密顿力学中的一种正则变换[3,4]。这样,拉格朗日函数非唯一确定性有什么物理意义的问题,可以算是说清楚了[13]。不过,文献[3,4]是以人们熟知的电磁规范问题为例来进行的来证明的。更普通的情形,即哈密顿正则运动方程也是拉格朗日函数非唯一性相关的规范变换下不变,则由Goldstein 在其所著的著名经典力学教材[5]中作为一道未给出解答的习题留下。由此,引发了相关文献和网络媒体上的许多争论[6-10]。本文从阐明拉格朗日函数非唯一性等价于动力学系统广义规范(以下仍简称规范)选择的任意性出发,通过分析各种争议的物理本质,证明无论拉格朗日方程还是哈密顿正则运动方程都具有这广义规范变换不变性,并澄清相关争论。

1 拉格朗日运动方程的广义规范协变性

首先从大家所熟知的电磁规范说起[3,4]。我们知道,电磁场可直接测量的物理量是电场强度E和磁感应强度B,所以带电粒子在电磁场中的牛顿运动方程为

其中,m为带电粒子的质量,Q为粒子所带电量。在分析力学中,这个运动方程也可由如下的拉格朗日函数

所满足的拉格朗日方程

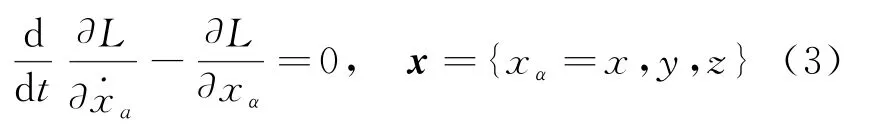
导出。这里,A和φ分别是通过如下关系

所定义的电磁矢势和标势。众所周知的是,与确定的电磁场强度(E,B)对应的电磁势(A,φ)并不是唯一确定的。也就是说,在电磁势规范变换

下,电磁场强度(E,B)是不变的,所以带电粒子的牛顿运动方程(1)是电磁规范变换式(4)下是不变的。这里χ,（xt）是电磁规范函数,可对时间变量t求全微商。可见,电磁势具有非唯一性,选定A和φ就称为选定一种电磁规范。

将式(4)代入方程(2)得到规范函数χ,（xt）相关的新拉氏函数

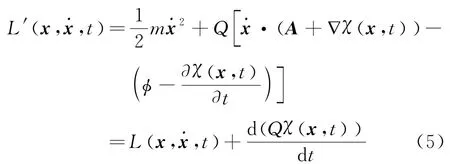
式中最后一项就是规范函数χ,（xt）的时间全微分项

容易证明,由这个新的拉格朗日函数所满足的拉格朗日方程

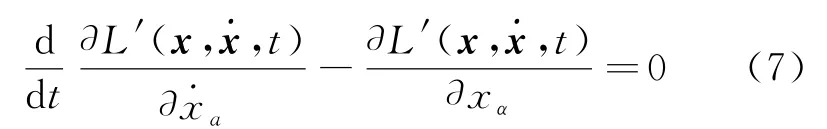
也可导出牛顿运动方程(1)。因此,我们说,牛顿运动方程(1)是电磁规范变换式(4)不变的,而拉格朗日方程(7)则是电磁规范变换式(4)下原拉格朗日方程(3)的协变形式。所以,对带电粒子在电磁场中运动的动力学问题而言,拉格朗日方程是电磁规范协变的。

推而广之,下面我们讨论广义力学系统中的拉格朗日函数的非唯一确定性问题[5,11,13]。也就是说,相差任意一个广义坐标和时间函数的时间全微分项的两个拉格朗日函数对应于同一个拉格朗日运动方程。为简便起见,我们只讨论单自由度系统。这种非确定性具体表现在,变换

下,拉格朗日方程

不变,即L和L′对 应于同一个拉格朗日方程。式(8)中,F(q,t)为广义坐标和时间任意函数的时间全微分,具有如下性质

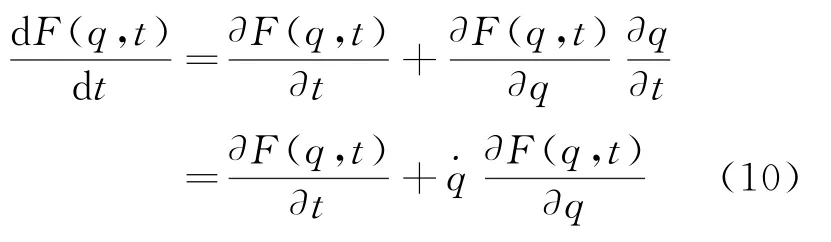
将式(8)与式(5),式(10)与式(6)类比,我们可以把式(8)定义为一种比电磁规范更广义的规范变换,即广义规范变换(以下仍简称规范),F(q,t)称为广义规范函数。对应的规范势是:AF（q,t）=∂F(q,t)/∂q和φF（q,t）=-∂F(q,t)/∂t。对三维力学系统,在笛卡尔坐标系中可定义与规范变换式(8)相关的规范矢势和规范标势

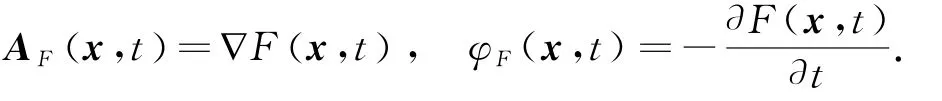
可见,拉格朗日函数的不确定性,实际上也意味着规范选择的任意性。

关于规范变换下拉格朗日方程(9)的不变性,大多数教材(如[5,11])都是从最小作用量原理出发利用定积分的变分为零边界条件来进行证明的。实际上,可以直接通过检验规范函数F(q,t)是否满足方程

即拉格朗日运动方程是规范协变的。

2 正则变换和规范变换的等价性

力学系统的动力学演化,不但可以用广义坐标和广义速度为自变量的拉格朗日态函数所满足的拉格朗日方程描述,也可以用正则坐标和正则动量为自变量的哈密顿量态函数所满足的正则运动方程刻画。两个态函数之间通过勒让德变换相联系,因此拉格朗日函数的不确定必然导致哈密顿量的不确定性。相比于上节相对简单明了的拉格朗日方程规范协变性证明,哈密顿正则运动方程广义协变性的证明则显得不那么显然[13]。大多数教材都没有给出论述[5,11],从而导致各种争议[6-10]。

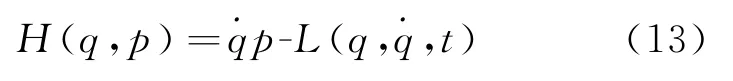
这里,p=∂L为 正 则 动 量。因 此,对应于规范变换式(8),哈密顿函数的规范变换形式为

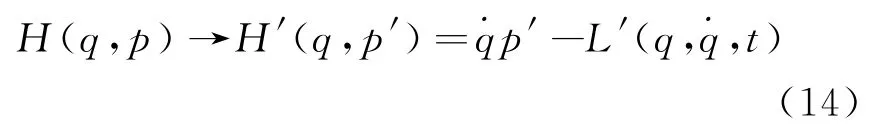
对应的正则动量是:p′=∂L′。正则运动方程的规范不变性意味着,哈密顿函数H(q,p)所对应的正则运动方程

在规范变换式(8)下应该协变为哈密顿函数H′(q,p′)所对应的正则运动方程

并且与原正则运动方程(15)应当等价,即

此外,(q,p)和(q,p′)的泊松括号关系也应该相等,即

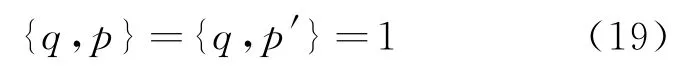
利用式(10)不难证明,p,p′满足关系:

这说明,拉格朗日函数的不确定性导致广义动量和哈密顿量也是不确定的。

正则运动方程的规范协变性,在大多数教材和实际教学中被认为是理所当然而无需具体证明。比如,在著名的经典力学教材[5]中这个问题只是作为一道习题列出,但并未给出解答,从而引起了很多争论。在著名物理教学期刊Eur.J.Phys.上曾经发表过一篇题为“Gauge transformations are canonical transformations”论文[6],宣称证明了这种规范变换就是正则变换。但遗憾的是,该文中所证明的规范不变“正则运动方程”

实际上并不是要证明的规范变换下正则运动方程的等价性关系式(17)～式(18)。注意,这里哈密顿函数是对广义坐标和广义动量的时间导数求偏导,而不是标准正则运动方程中的对广义坐标和广义动量本身求偏导,所以此文中的证明是错误的。针对文献[6]中的这一错误,文献[7]宣称:“In this short paper we address the question whether the transformation that leaves the Euler-Lagrange equation of motion invariant is also a canonical transformation and show that it is not.”,从而得出规范变换不是正则变换的结论:“Gauge transformations are not cannoical transformations”,与著名教材[5]中的命题相悖。由此在网络上引起了很多争论[7-10],有待澄清。

等价性方程(17)的证明是非常简单的。因为规范函数F(q,t)不是p,p′的显函数,所以利用方程(20)～方程(21)容易得到

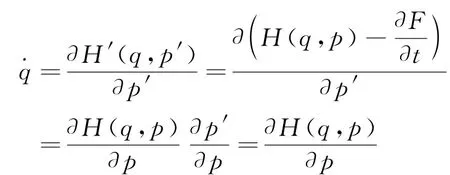
这就证明了等价性关系式(17)。

但是,等价性关系(18)的证明就不那么直接了,是文献和网络上争论的焦点所在。在排除文献[6]错误证明的基础上,文献[7]简单地利用方程式(21)推导得到

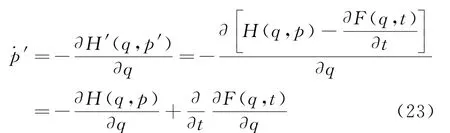
它与直接由方程(20)所得到的结果

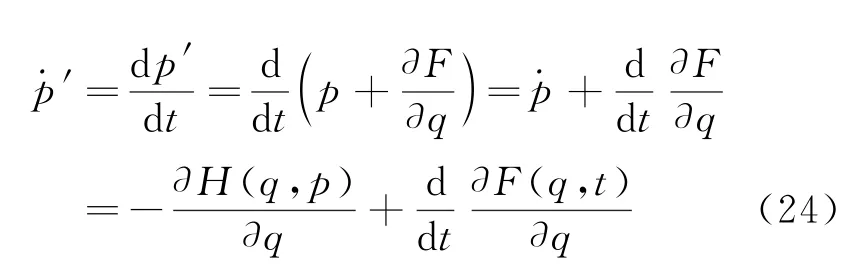
显然是不相容的。文献[7]因此得出了“规范变换不是正则变换”的结论,与文献[5]的命题相悖。证明文献[5]命题的一个简单方法[8]是,假定p′不是q的显函数,从而利用勒让德变换及规范变换式(8)可得

代入上式便可得到方程(18),从而证明了文献[5]中的命题。值得指出的是,这一证明方法所假定的p′不是q显函数,从而满足∂p′/∂q=0的条件,当且仅当规范函数F(q,t) 是q的线性函数时才成立[13]。一般地,由式(20)可得

考虑这一性质,文献[9,10,13]虽然给出了等价性关系式(18)的证明,但稍显繁琐不够清晰。下面我们给出其简洁证明。首先,利用偏微分运算的链式法则和规范变换关系式(21),我们有

其次,利用上面已经证明过的等价性关系式(17)及p′与q的关系式(20),容易得到

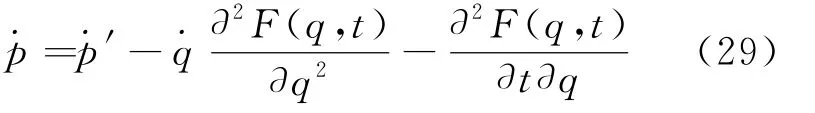
最后利用全微分公式

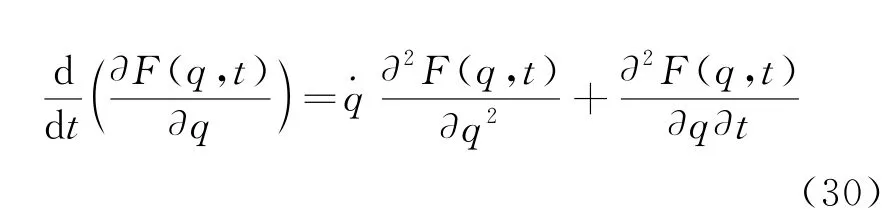
就可以得到期望证明的方程(24)以及等价性关系式(18)。至此,我们完成了规范变换下的哈密顿正则方程的协变性证明。回过头去看文献[7]的错误所在,是由于方程(23)中忽视了新规范下(这时p′与q是一对共轭变量)p通过式(20)已经变成是q的函数了,所以由方程(10)、方程(20)应将方程(23)修改为

这正是方程(24)。

当然,这一规范协变性意味着规范变换下泊松括号也是不变性。确实,按照任意正则变量函数f(q,p),g(q,p)的泊松括号定义

这就证明了泊松括号运算的规范协变性,它是以上所证明等价性的一种必然推论[12,13]。注意,这里并不要求=0 (即规范函数F(q,t) 并不需要仅是q的线性函数)[13]。这说明,如果q,p是一对对应哈密顿函数H(q,p) 的共轭正则变量,那么q,p′则是一对对应于哈密顿函数是H′(q,p′)的共轭正则变量。

综上所述,拉格朗日函数非唯一性确实可以看作是一种规范不确定性,在这种规范变换下,拉格朗日运动方程、哈密顿正则运动方程和泊松括号等都是协变的。因此,与拉格朗日函数非唯一确定性相关的规范变换就是一种正则变换。

3 结语

本文系统讨论了经典力学体系中力学系统普遍存在的拉格朗日函数不确定性问题的物理意义。结果表明,这种不确定性实际上可归结于系统动力学描述的规范不确定性,它可看作是通常电磁规范的一种自然推广。与这种不确定性对应的运动方程(无论是拉格朗日方程还是哈密顿正则运动方程)不变性可以归结其形式在相应规范变换下的协变性。因此,与拉格朗日函数唯一性所对应的规范协变性确实可以看作是一种正则变换,由此澄清了文献和网络上这一问题的一些争议。

当然,需要说明的是,物理系统的运动规律不仅仅取决于其运动方程,还与其所蕴含的对称性和热力学特性等因素有关。所以,对一个力学系统的拉格朗日函数只是做一些数学形式上的变换并不一定能完全揭示系统的动力学性质。比如,如果我们在一个拉格朗日函数中添加一个拓扑项,就会破坏系统对性。尽管这个拓扑项并不改变运动方程,但是它的存在意味着理论上它描述了不同于物理系统。这些问题超出了本文议题,在此不再深入讨论。