运动电荷的电/磁场高斯定理的直接验证

周国全 祁 宁

(武汉大学物理科学与技术学院,湖北 武汉 430072)

电荷之间的库仑力,是自然界中已知的两种典型的平方反比有心力系统之一,这类有心力系统,除了满足一般有心力系统所具有的普遍性质,还满足平方反比有心力系统所独具的Runge-lenz(隆格-楞次)守恒矢量和高斯定理[1-5]。关于平方反比的有心力系统的Runge-lenz守恒矢量性质及其应用,文献[6-8]作了详尽介绍。静电场的高斯定理,证明简单,应用广泛,深入人心[1-5]。通过引入在洛伦兹规范下的四维矢势Aμ,μ=1,2,3,4和电磁场二阶张量Fμν,(μ,ν=1,2,3,4),电磁场的相对论协变性理论得以完备建立,麦克斯韦方程组也得以改写为相对论协变的张量形式,这已然保证高斯定理对任何惯性参考系均能成立[2]。也就是说高斯定理的微分与积分形式,无论对于静止电荷还是运动电荷,都已自然成立,原本无须额外的专门证明。然而在大学物理教学中,广大师生对此定理与惯性参考系的无关性仍然缺乏直接的验证和直观的体会。这个问题现有教材鲜有提及,更少强调[1-4]。为使学习和讲授大学物理课程的广大师生对此知识点有完整而清晰的思路和掌握,本文分享一点作者的教学心得,针对匀速运动点电荷的电/磁场的高斯定理的相对论协变性进行直接验算。

1 电磁场的高斯定理的相对论协变形式

在洛伦兹规范下引入四维电磁矢势Aμ=(A1,A2,A3,A4)=(A,iφ/c)=(Ax,Ay,Az,iφ/c),其中(Ax,Ay,Az)为电磁矢势A;φ为电磁标势;而电场强度E、磁感强度B与矢势A、标势φ之间关系为:

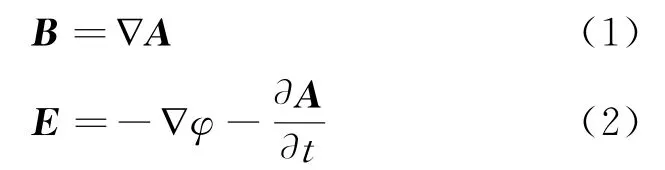
它可以改写为四维协变形式。定义电磁场二阶张量

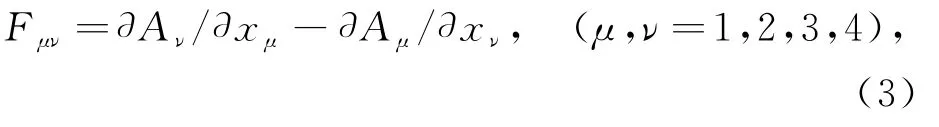
其中xμ=(x,y,z,ict)=(x1,x2,x3,x4)为四维空间坐标,电场强度E、磁感强度B的分量正是反对称二阶电磁场张量Fμν的六个独立分量。麦氏方程组的四个方程可以改写为协变形式

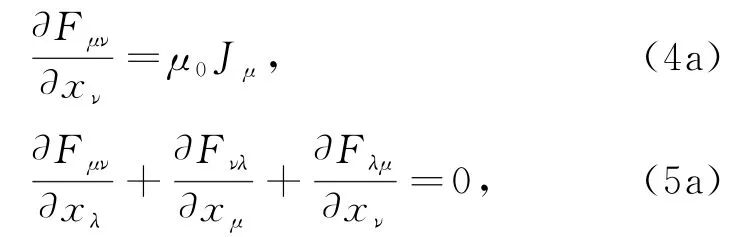
其中Jμ=(jx,jy,jz,icρ)是四维电流密度矢量。而电场高斯定理的微分形式

正是(4a)的第四个分量等式(μ=4分量);而磁场的高斯定理的微分形式

正是协变方程(5a)式当μ,ν,λ分别取1、2、3时的分量等式(还有另外5个分量等式亦然)。

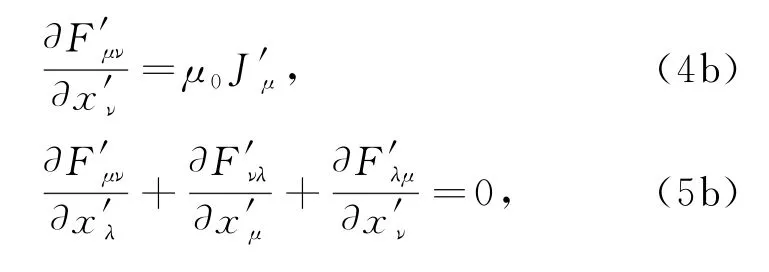
我们知道,在Minkowski四维空间中,只要把电磁学物理量写为相应的四维张量形式,电磁学规律方程就自然地表达为四维协变形式的方程。根据四维张量方程的协便理论,当它从一个惯性系S变换到另一惯性系S′后,它将自然地保持数学形式不变。因此式(4a)、(5a)在惯性系S′依然成立:于是在惯性系S′依然成立:张量方程(4b)的第四个分量等式(μ=4分量)就是S′系电场的高斯定理的微分形式∇′E′=ρ′/ε0;张量方程(5b)当μ,ν,λ分别取1、2、3时的分量等式就是磁场的高斯定理的微分形式∇′B′=0。这就是电磁学规律的相对性协变规律。从而电磁场的高斯定理在任何惯性系都成立。再用散度定理可以证明式(6)、(7)对应的积分形式的高斯定理在S′系也形式不变。然而这并非高斯定理的直接验算,读者未能得到直观的感受。

2 匀速运动电荷的电/磁场

我们首先借助于电磁场二阶张量的相对论变换,从静止点电荷的纯电场出发,求出匀速运动点电荷的电、磁场[2-3]。

一个电量为q的点电荷在惯性系S中以速率v沿X轴作匀速直线运动。与带电粒子相对静止的本体参考系为S′,它沿S系X轴以速率v匀速运动。再设在t=t′=0时,两坐标系原点重合,则在S′系中r′(x′,y′,z′)处带电粒子激发的电磁场为

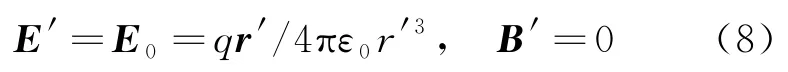
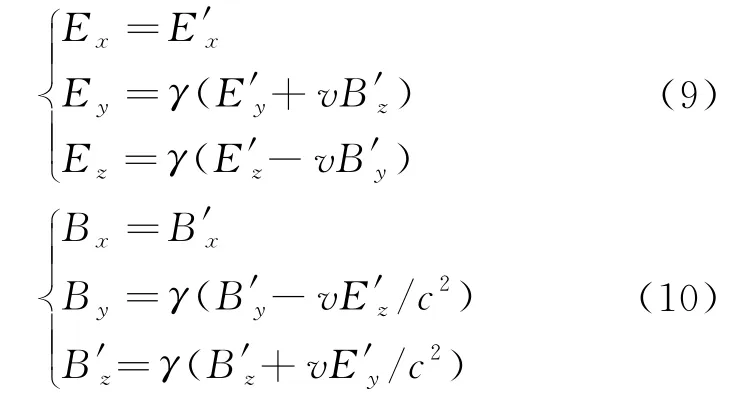
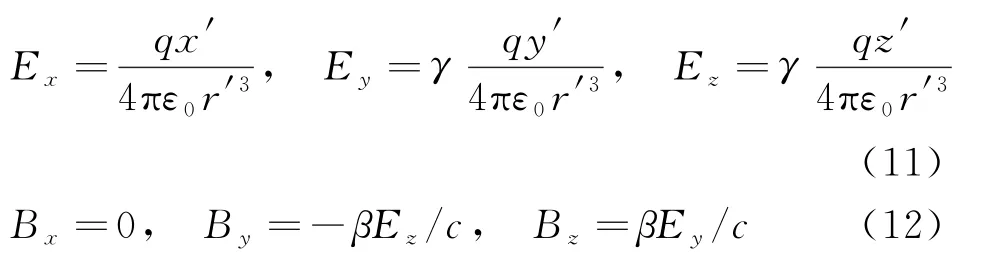
表达式 (12) 等价于如下等式

至此我们求出了在S系中匀速运动的点电荷的电磁场的表达式。注意以上诸式成立于同一世界点。在t=t′=0时,两个惯性参考系的空间坐标之间的洛伦兹变换为x′=γx;y′=y;z′=z。

3 匀速运动电荷的电场的高斯定理的直接验证

然后下一步,我们对于包围运动点电荷的一个任意封闭的高斯面σ,对此匀速运动点电荷的电场、磁场分别作通量积分,直接验证匀速运动点电荷的电/磁场的高斯定理。由于

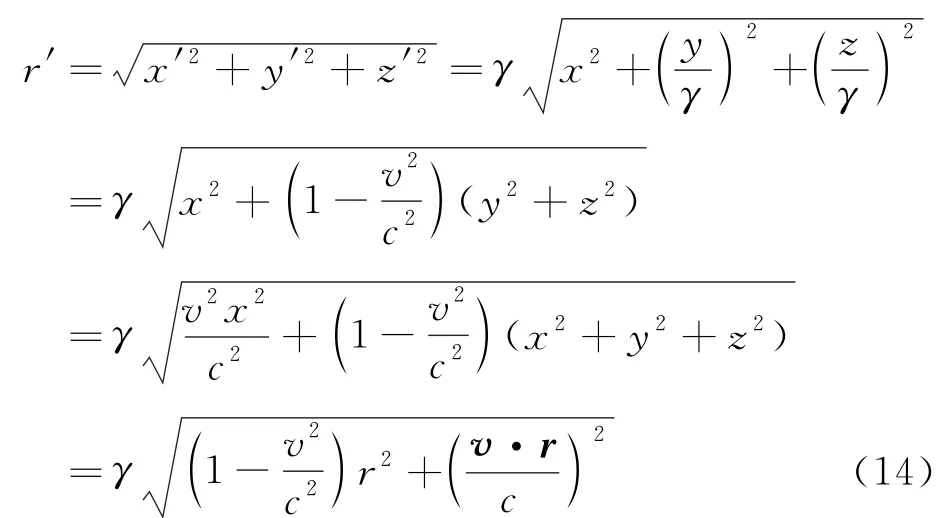
因此式(11)中的电场强度E可以改写为如下形式:

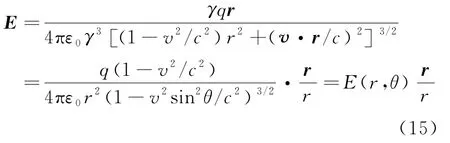
上式中θ是υ 与r的夹角。

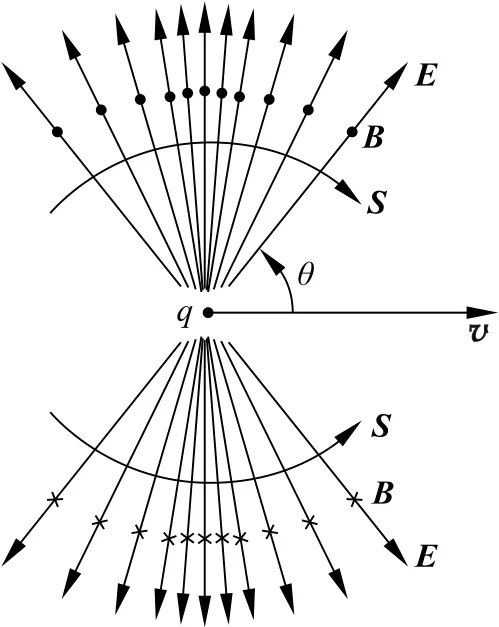
图1 运动点电荷的电场线与磁场线

结果表明,如图1所示,在S系中匀速运动点电荷的电磁场,其电场线的分布,再也不具有静止点电荷的电场线那样的球对称性分布特点,而是只剩下以运动方向为轴的转动不变性。易于发现场强的分布与θ角有关,在平行于v的θ=0 方向,场强E、B有极小值;在垂直于v的θ=π/2方向,场强E、B有极大值。当粒子运动速度υ 趋近于光速c时,电、磁场的场线就会向垂直于υ 的平面靠拢和集中,此时电磁场就如同一个沿υ 方向运动的平面冲击波。

通过直接积分,可以证明,在S系中,高斯定律依然成立。对于包围运动点电荷的一个任意封闭的高斯面σ,以点电荷在t=0时刻的位置O点为极坐标原点,以电荷速度方向为极轴(Z 轴)方向,取定极坐标系(r,θ,φ)。对于高斯面上处于r(r,θ,φ)处的高斯面元矢量dS=dSn,(其中n为面元矢量dS的法向单位矢量),电场强度对dS的元通量为

其中α=(r/r,n),是两个单位矢量之间的夹角;dSr=dScosα是面元矢量dS在垂直于r方向的投影面元大小,在以r为半径的球面上,面积元dSr=r2sinθdθdφ;因而有

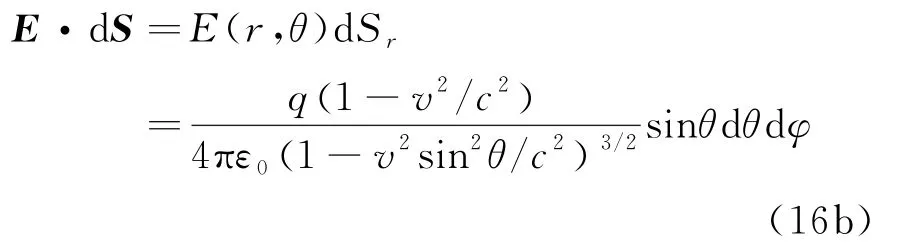
注意以上元通量与r无关。对此封闭高斯面求电场强度的通量积分可得

注意其中的变量代换x=cosθ∈[-1,1],且用到如下积分公式

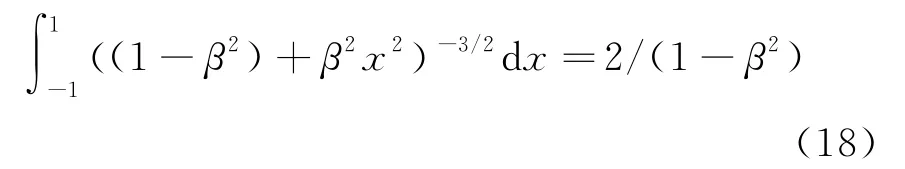
这就直接验证了匀速运动点电荷的高斯定理的积分形式。再运用微积分理论中的散度定理,极易将式(10)改写为相应的微分形式:

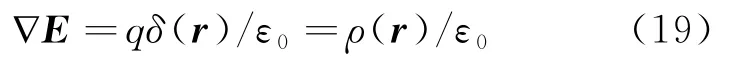
其中ρ(r)=qδ(r)是点电荷q在S系原点处的电荷体密度。至此我们直接验证了匀速运动点电荷的高斯定理的积/微分形式仍然成立。

4 匀速运动电荷的磁场的高斯定理的直接验证

首先对于以运动电荷为球心的任意球形高斯面σ,将匀速运动点电荷在S系B的表达式 (13)代入其高斯通量积分式可得:

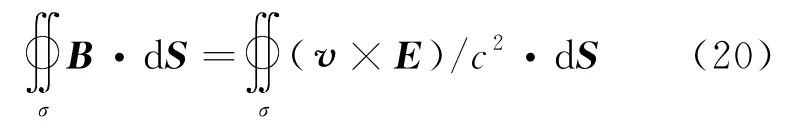
根据三矢量混合积的拉格朗日恒等式,可知

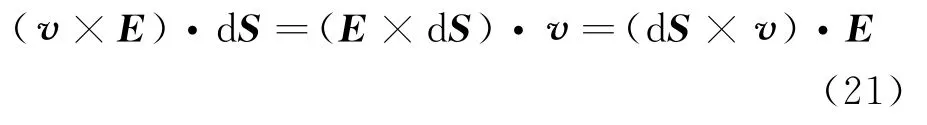
于是

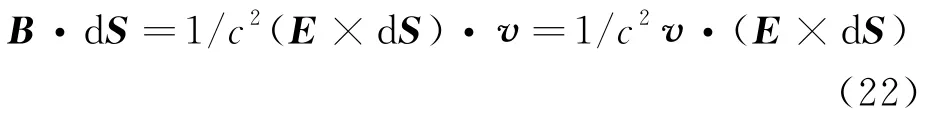
由于点乘对左右矢量都具有线性性质,v为常矢量,因此可从积分号内部提取出来,于是

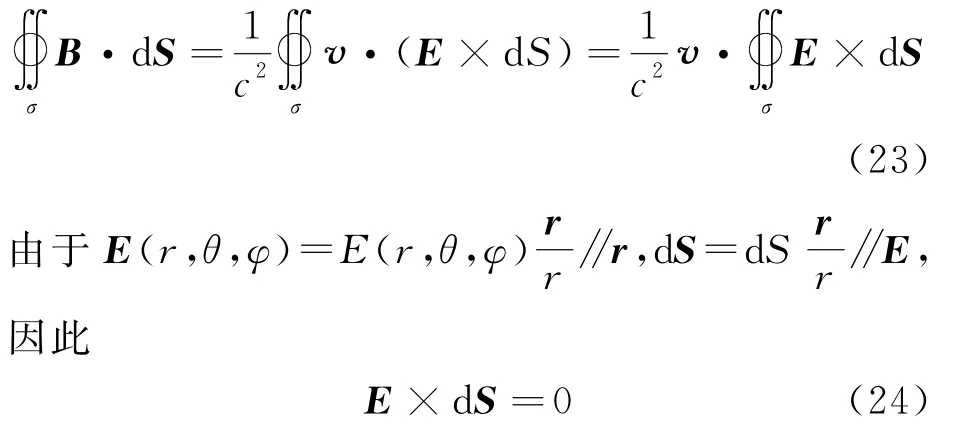
将式(24)代入式(23),即得运动电荷的磁场对于球形高斯面的高斯定理:

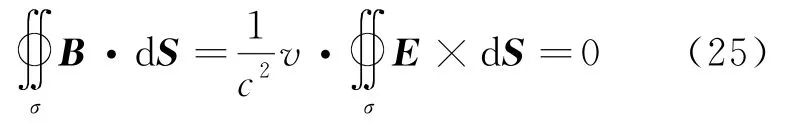
实际上对于包围运动电荷的任意形状高斯面Σ,同样可证磁场的高斯定理成立。再运用微积分理论中的散度定理,极易将式(25)改写为相应的微分形式:

至此,我们直接而成功地验证了匀速运动点电荷的磁感应强度的高斯定理仍然成立。

5 结语

本文通过电磁场张量的相对论变换的方式,从静止点电荷的电、磁场表达式出发,求得匀速运动点电荷电/磁场的表达式,然后针对包围运动点电荷的任意封闭高斯面(包括球形高斯面)情形,用直接积分的方式验证了匀速运动点电荷的电/磁场的高斯定理的积分形式,进而验证了其微分形式。作为麦克斯韦方程组的一部分,高斯定理成为电磁场与电磁波的理论基础,应用广泛,影响深远。直接验证匀速运动点电荷的高斯定理的协变性,会使理工科大学生对电磁场理论的相对论协变性有深刻体会,也使大中学普物教师对电磁场理论的逻辑脉络了然于心,在教学中运用自如。