基于扰动补偿的连续搅拌釜式反应器自适应积分滑模控制
2021-05-06王素珍刘建锋孙国法代明星靳奉祥
王素珍, 刘建锋, 孙国法, 代明星, 靳奉祥
(1. 青岛理工大学 信息与控制工程学院, 山东 青岛 266520; 2. 山东建筑大学 测绘地理信息学院, 山东 济南 250101)
连续搅拌釜式反应器(CSTR)是石油化工、制药、废水处理等诸多工业生产的反应设备[1],其控制效果对最终产品的质量起着至关重要的作用。该系统是一个非常复杂的被控对象,在实际过程中经常受到各种因素的影响,如反应物浓度变化、副反应、温度和气液相位不均、外扰等,导致系统存在许多未知的不确定项以及不可测状态,整个系统呈现高度的非线性,因此其控制器的设计难度非常大。
比例积分微分(PID)[2-3]控制器具有配置简单、易于实现等优点,在工业控制领域应用非常广泛,但是,随着控制要求的不断提高,PID控制器已经越来越难以满足系统控制精度的要求。近年来,随着控制理论的不断发展,国内外学者陆续将诸如模糊控制[4]、自抗扰控制[5]、鲁棒自适应控制[6]等先进的控制方法引入到CSTR系统控制中。文献[7]中通过将CSTR系统模型辨识成一个Takagi-Sugeno(T-S)模糊模型来逼近系统中的非线性函数,利用线性控制理论方法进行分析,但是非线性系统模型近似线性化后存在拟合问题,在实际应用中难以对系统的未知非线性函数进行有效的逼近。针对这个问题,许多学者又将预测控制[8-9]的方法引入到CSTR系统的控制中,在一定程度上提高了系统的鲁棒性,弥补了建模所带来的不足;但是,预测控制多为线性模型,没有对系统的未知状态和未知非线性函数项进行有效的处理,因此在实际应用时具有很大的局限性。随着神经网络或模糊逻辑系统的大量应用[10-12],研究人员基于神经网络或模糊逻辑系统的逼近特性,针对CSTR系统提出了许多控制方法。Salehi等[13-14]设计了2种自适应模糊温度控制器,基于模糊逻辑系统逼近被控系统中浓度的依赖项以及一些未知参数,实现了较好的控制效果,但这些方法并没有很好的抗干扰能力,系统鲁棒性不强。
滑模变结构控制具有特殊的结构,使得滑模控制具有非常强的鲁棒性。近年来,针对CSTR系统采用滑模控制的方案越来越多[15-16],取得了非常好的控制效果,但是这些控制方案依旧是在假设系统状态已知的情况下,并且所采用的滑模控制方案产生明显的抖振现象,严重影响了控制效果。
针对以上问题,本文中基于一类非线性CSTR系统,结合滑模变结构控制,提出一种自适应积分滑模控制算法(简称本文控制算法),对CSTR进行分析并建立数学系统模型,根据系统中的未知状态量以及各种未知扰动分别设计有限时间状态观测器以及扰动观测器,实现对被控对象未知状态量的观测以及系统扰动信号的估计,有效提高系统的抗干扰性能。另外,通过引入积分滑模面,设计自适应变比例增益趋近律来抑制系统中的抖振,同时利用Lyapunov函数证明系统的稳定性,通过数值仿真对该控制方法的有效性进行验证。
1 模型描述及准备工作
1.1 系统模型结构描述
CSTR是化工过程中重要的反应器,其控制是化工工艺流程最重要、最难掌握的环节。CSTR系统结构如图1所示。按照一定比例混合的原料经过预热后进入反应器,在一定的温度下进行聚合放热反应。通常情况下,CSTR系统在稳定状态下操作,内容物充分混合,因此建模不涉及整个容器中浓度、温度或反应速率的显著变化。本文中将系统视为一个放热、不可逆的一阶反应A→B,其中A为反应物,B为反应产物。为了便于建模,针对该系统提出以下假设。
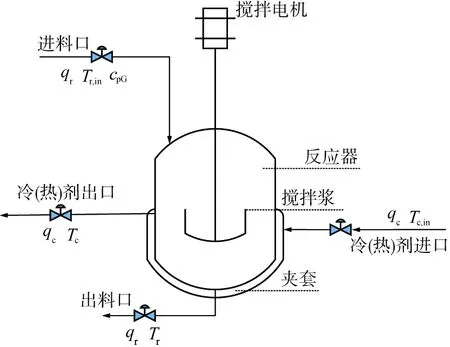
qr—进(出)料口物料体积流量; Tr,in—进料口物料温度; cpG—进料口物料浓度; qc—冷(热)剂进出口流量; Tc—冷(热)剂出口温度; Tc, in—冷(热)剂进口温度; Tr—出料口温度。图1 连续搅拌釜式反应器结构示意图
假设1:假设CSTR进料充分混合,反应器内的温度和浓度都是相同的,物料比热容和传热系数始终不变,进、出口流量在稳态和动态时处处相等,即反应器内液位保持不变,热损失忽略不计。
假设2:反应物具有恒定的密度和容量,且反应前后CSTR内物料的总体积不变。根据物质和能量守恒定理,CSTR内发生的放热、不可逆的一阶反应可以被表示为
(1)
式中:R为摩尔气体常数; ΔH为反应放出的热量;k0、T和CA分别是反应速率常数、反应温度和反应后反应物A的浓度;h为反应釜内液位高;S为反应釜截面积;E为活化能;V为反应釜体积容量;Tf为冷(热)剂入口温度;Tc为冷(热)剂出口温度;CAf、F、Cp及ρ分别为反应物A的入口浓度、稳态流动速率、比热容及CSTR内浓度。为了便于控制器的设计,CSTR系统模型(1)可继续转化[17]为
(2)
式中:x1、x2为CSTR系统的状态变量;B为绝热温升;Da为达姆科勒数;β为热传递系数;γ为活化能与平均动能之比;x2c为系统初始状态;u为系统控制信号的输入;d1、d2为CSTR系统的2个未知扰动信号;y为系统的输出。
为了便于后期的对控制器的设计,针对模型(2)提出假设3。
假设3:对于系统(2)的任何一个可能的参考信号xr,di的n+1-i次微分都是有界的,即
式中:ζ>0为已知常数;Cn+1-i为所有的微分函数集合。
2 有限时间状态观测器设计
由于CSTR系统模型中很多参数在实际过程中难以测得,因此,被控系统的状态变量是未知的。为了便于控制器的设计,本文中基于文献[18]已有的成果,引入一类有限时间状态观测器,从而实现对被控系统未知状态的估计。
针对系统(2),设计状态观测器为
(3)

定义观测器的观测误差为
ε=x-z,
(4)
式中:ε=[ε1,ε2]T;x=[x1,x2]T;z=[z1,z2]T。
对ε求导得
(5)
稳定性证明:首先针对误差ε2选取Lyapunov函数
(6)
对式(6)求导得
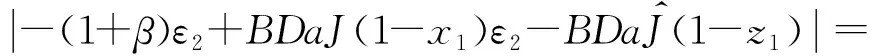
-|ε2|(k2-|-(1+β)ε2+BDaJ(1-x1)ε2-
(7)

(8)
针对误差ε1选取Lyapunov函数
(9)
对式(9)求导,得
(10)
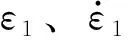
3 滑模控制器设计
3.1 扰动观测及补偿
为了进一步提高控制器的控制性能,增强系统鲁棒性,基于Levent微分器[19]设计一类扰动观测器,以便对系统模型(2)中的扰动信号进行估计补偿。所设计的扰动观测器具体形式为
(11)
式中:φi(i=1,2,…,n)为系统内部状态;Ui为扰动观测器原始微分信号第i+1阶微分估计值;λi为扰动观测器增益系数;D(t)为扰动观测器输入的微分信号函数,且D(t)存在n阶导数存在且有界,即|D(n+1)(t)|≤Γ,Γ为正常数。为了保证扰动观测器的观测效果,观测器(11)的增益系数λi需慎重选择,基于文献[20]提出可行的参数选取规则,如表1所示。

表1 扰动观测器增益系数选取规则
由于未知扰动di满足假设3中的条件,因此扰动信号可以在有限时间内通过扰动观测器(11)估计获得,即
(12)
3.2 自适应积分滑模控制器设计
滑模控制具有非常强的鲁棒性,在处理非线性系统中的不确定项以及未知扰动等方面有着独特的优势。本文中将基于上述状态观测器的观测结果以及扰动观测器的估计结果对未知扰动信号进行补偿,并设计一类自适应积分滑模控制器。
定义被控系统(2)的跟踪误差e为
e=z2-xr
,
(13)
式中xr为系统的输出参考信号。基于状态观测器和扰动观测器的观测结果,对式(13)求导,得
(14)
定义一个积分滑模面
(15)
式中k为滑模修正系数。
对式(15)求导,得
(16)

(17)
式中Ueq为等效控制信号。
设计一种新的自适应变比例增益的趋近律,与传统的等速趋近律相比,自适应变比例增益的方法不仅能使被控系统快速收敛,而且能有效抑制滑模控制中的抖振现象。该趋近律具体设计如下:
(18)
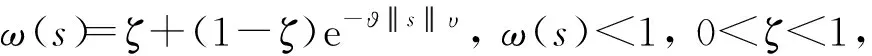
设计自适应更新律为
(19)
式中η为大于0的常数,则
(20)
式中Us为鲁棒项控制信号。最终得到自适应积分滑模控制器的控制律为
u=ueq+us。
(21)
将式(17)、(20)、(21)代入式(16),得
(22)
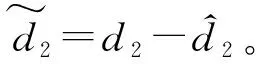
假设4:假设扰动观测误差有界,且
其中0<ζ<1。

(23)
对V1求导,得
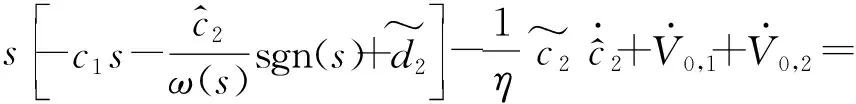
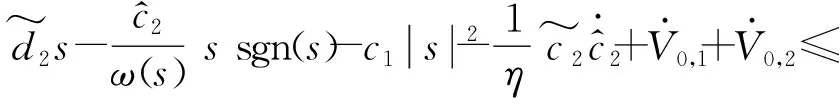
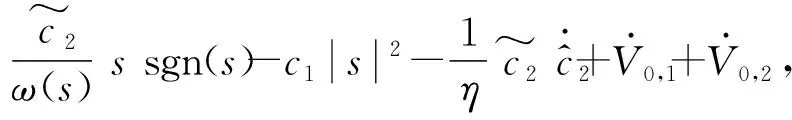
(24)
将式(22)代入式(24),化简得
(25)
4 仿真
以下将通过具体的仿真算例对本文所提控制方法的有效性进行验证。仿真时,系统模型的参数分别设置为B=8,β=0.3,γ=20,Da=0.078,x2c=0。系统期望的轨迹信号xr和系统的外部扰动d1与d2分别设置为
(26)
具体仿真结果如图2—4所示。由图2中系统输出信号跟踪效果图可以看出,系统输出信号能够在有限时间内精确地跟踪所期望的轨迹信号,且跟踪误差e能在有限时间内收敛到0附近的小邻域内,验证了本文控制算法能对系统信号实现有效的跟踪。

(a)输出信号x2跟踪效果
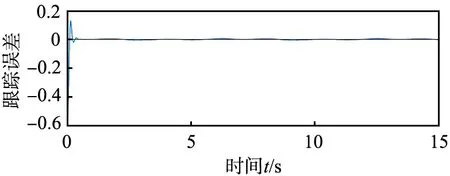
(b)输出信号x2跟踪误差图2 系统输出x2的跟踪效果及误差
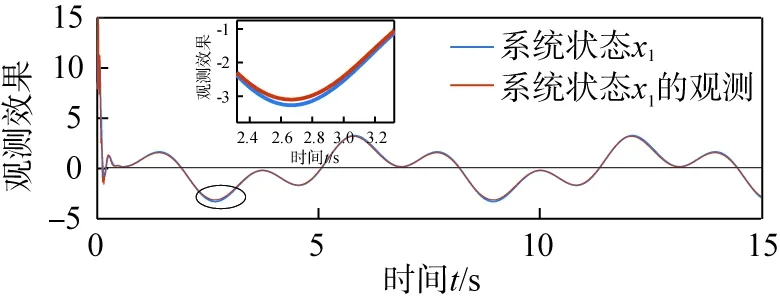
(a)系统状态x1及其观测信号
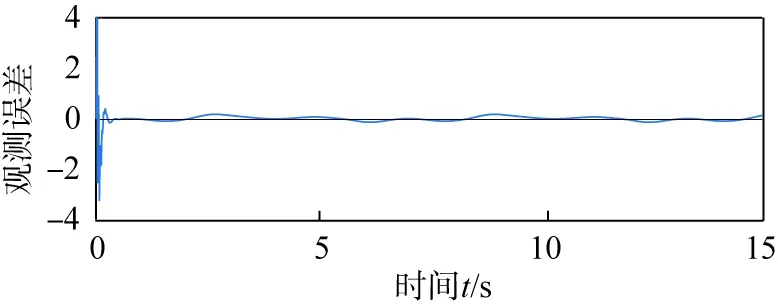
(b)观测误差图3 系统状态x1观测效果
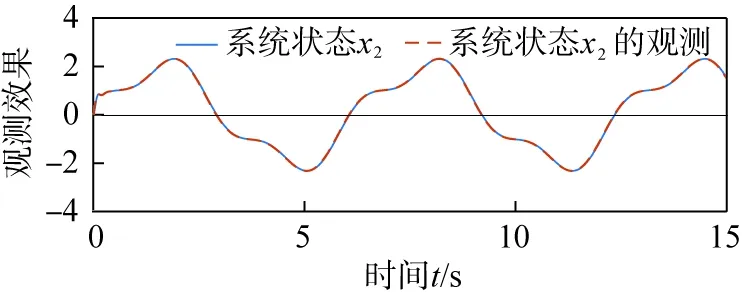
(a)系统状态x2及其观测信号

(b)观测误差图4 系统状态x2观测效果
由有限时间状态观测器对系统未知状态的观测效果的仿真结果(图3、4)可以看出,所设计的有限时间状态观测器对被控系统内含有的未知状态量可以实现较好的观测估计,并且观测误差可以收敛在一个很小的范围内。
根据表1合理选择扰动观测器的增益系数,并利用观测器(11)对系统未知扰动进行估计,仿真结果如图5所示。从图中可以看出,扰动观测器能够实现在有限时间内对系统未知扰动的高精度估计。

(a)系统状态d1的观测效果

(b)系统状态d1的观测效果图5 系统扰动观测效果
此外,为了进一步验证其算法的扰动补偿控制效果,分别采用无扰动补偿的本文控制算法(d1=d2=0)和本文控制算法对建立的CSTR系统(2)实现反馈控制来进行对比仿真验证,结果如图6所示。由图可以明显看出,当系统采用带有扰动补偿作用的控制方法时,系统的控制性能较好,超调量更小。
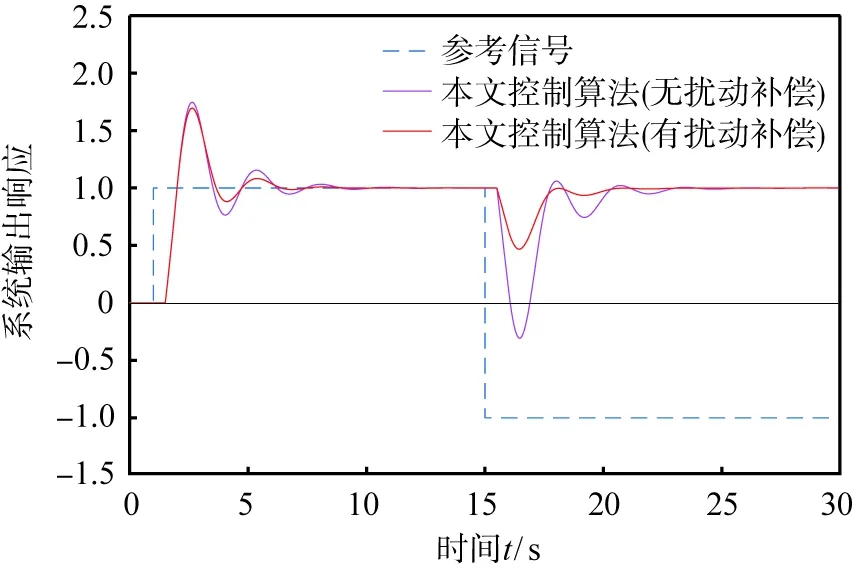
图6 系统扰动补偿控制效果
考虑到实际工业CSTR系统控制输入信号存在的抖振现象,为了验证本文控制算法对抖振信号的抑制作用,令系统期望输出信号为方波信号x2r,利用MATLAB软件对系统进行仿真验证,其控制效果如图7所示。由图可知,系统输出信号y能够快速且有效地跟踪上x2r,控制输入信号抑制效果明显。
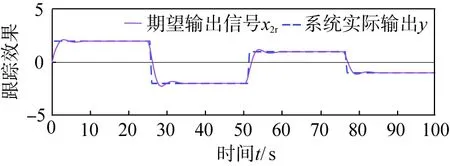
(a)系统跟踪效果
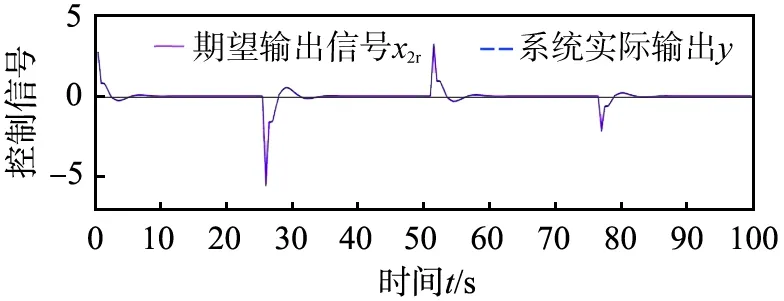
(b)控制输入信号图7 系统抖振控制效果
为了更好地验证所提控制方法的抗干扰能力及动态性能,分别利用本文控制算法与已有的自抗扰控制算法及传统PID控制算法对同一阶跃信号进行跟踪,并计算上述3种算法在阶跃响应下的峰值时间、调节时间以及超调量,结果如表2所示。与此同时,在被控系统稳定后25~27 s时施加额外的外部干扰,信号跟踪效果如图8所示。
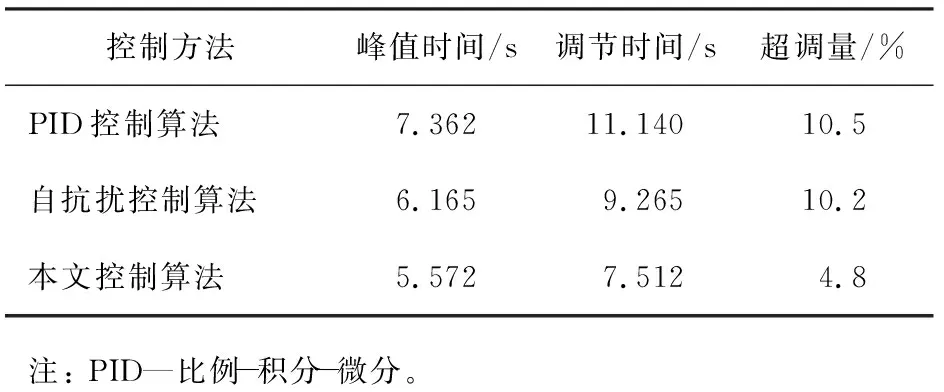
表2 连续搅拌釜式反应器系统的动态性能指标
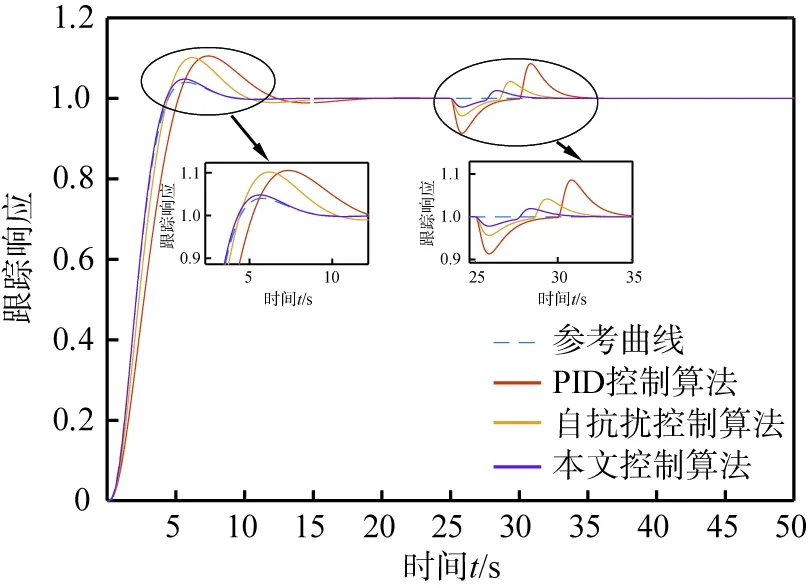
PID—比例-积分-微分。图8 施加外部干扰后的跟踪效果对比
由表2和图8可以看出,本文控制算法与PID控制方法以及自抗扰控制方法相比具有更好的动态性能,主要表现在: 1)超调量更小,调节时间短且系统响应速度快,能够快速地跟踪参考信号; 2)当被控系统突然面临未知的外部扰动时,本文控制算法超调量最小,且能够更快地控制被控系统稳定,抗干扰能力更强。
5 结语
针对一类非线性CSTR系统中的控制问题,本文中提出了一种基于扰动补偿的自适应积分滑模控制算法。根据CSTR建立的数学动态模型转化为非线性系统状态空间方程,利用建立的系统模型分别设计了有限时间状态观测器和扰动观测器,实现了对系统未知状态的观测以及未知扰动的估计补偿,增强了系统鲁棒性。基于积分滑模面设计的自适应变比例增益趋近律,有效地抑制了系统中产生的抖振,并通过Lyapunov函数证明了闭环系统的稳定性。仿真结果验证了本文控制算法具有良好的抗干扰性能。
