基于主成分分析-孪生支持向量机的工业系统故障监测

朱振杰， 杜付鑫, 杨旺功

(1. 山东大学 a. 高效洁净机械制造教育部重点实验室，b. 机械工程国家级实验教学示范中心，c. 机械工程学院，山东 济南 250061； 2. 北京林业大学 信息学院，北京 100083)

工业4.0概念的提出代表着智能化时代的来临。为了适应世界制造产业的发展新需求，我国需要利用各种信息化技术手段促进工业制造产业的新变革[1]； 但是，随着各种设备不断增多并趋于更加智能化，现代工业系统变得越来越复杂，在整个系统运行过程中发生各种各样故障的概率也越来越大，在某些情况下可能引起系统的整体瘫痪[2]，因此，必须对工业系统进行实时、准确的监测，从而保证系统安全稳定运行[3-4]。

工业系统的监测任务需要对出现故障进行及时检测与识别，但是，现代工业系统十分复杂，故障的检测与识别面临巨大的挑战。传统的监测方法存在故障检测精度不高、处理速度慢的问题。此外，大部分监测方法仅进行故障检测，对故障的类型无法做到准确识别[5-6]，机器学习技术作为一种先进的计算机辅助手段[7-9]，能够有效解决该问题，对此，研究人员提出了许多的相关方法。例如，张成等[10]提出了一种基于加权k近邻(KNN)规则的多模态间歇过程故障检测方法，将原始数据投影到低维空间，对过程数据进行降维以便降低计算复杂度，然后通过加权KNN聚类完成过程故障检测任务。作为一种使用最广泛的数据降维算法，多元统计的主成分分析(PCA)在高维数据特征提取方面具有优异的性能，因此,赵晓君等[11]提出将PCA和KNN聚类相结合设计了一种通用的在线故障诊断算法。类似地，Yang等[12]提出了基于PCA-支持向量机的生物化学产品制造过程故障诊断与检测方法，同样得到了较好的准确性。

孪生支持向量机(twin support vector machine，TWSVM)是一种新型的基于统计学习理论的机器学习方法[13]。作为传统SVM的一种变形算法，TWSVM不仅继承了其优秀的学习能力，而且运行效率提高了4倍。本文中利用PCA-TWSVM实现故障类型的识别。首先，采用PCA方法对涉及的复杂故障变量进行降维，并对提取的主要故障变量进行判断，完成故障检测；然后，利用TWSVM进行故障类型的识别，结合PCA方法实现系统监测，进一步改善工业系统故障的识别综合性能。

1 基于PCA的变量降维

在进行常规的Logistic回归分析之前，本文中利用统计产品与服务解决方案软件SPSS 19.0 的PCA主成分提取功能来进行故障变量的数据降维，操作界面如图1所示。

作为一种最常用的线性降维方法，PCA能够在尽量保证信息量不丢失的情况下，通过投影对原始特征进行降维。假设模型样本由工业系统故障特征变量构成，每个样本有n个特征，需要从这些特征变量中提取主要影响因子。m个训练样本为x1,x2,…,xm，对应的标准差为S1,S2, …,Sm, 那么标准化变换的方法为

图1 统计产品与服务解决方案软件SPSS19.0的主成分分析降维操作界面

Yj=aj1x1+aj2x2+…+ajmxm,j=1,2,…,m，

(1)

式中ajm为训练样本xm对应的系数因子。

从j=1开始依次对式(1)的变换结果进行主成分分析。首先，如果Y1的数值等于相应特征值的正交单位向量的2范数，且Y1的方差最大，则可以确定Y1为第一主成分；其次，如果Y2的数值等于相应特征值的正交单位向量的2范数，Y1与Y2的协方差为0且Y2的方差最大，则可以确定Y2为第二主成分。按照上述方法重复进行m次，以此类推可以得到多个主成分。

在累积方差贡献率计算过程中，第i个主成分Yi的贡献率ηi为

(2)

则前m个主成分的总贡献率c为

(3)

式中：λi为主成分矩阵的特征值；k为保留主成分个数。

图2为累积方差贡献率示意图，一般情况下确保c的值大于85%。在这个条件下可以确保损失的

图2 累积方差贡献率示意图

信息不至于太多，也能够达到减少变量、简化数据结构的目的，提取出反映工业系统整体过程的前k个主成分。以其中一个公因子为例，其统计分析的表达式为

F1=-0.16Z1+0.161Z2+0.145Z3+0.199Z4-

0.131Z5-0.167Z6+0.137Z7+0.174Z8+

0.131Z9-0.037Z7+0.174Z8+0.131Z9-

0.037Z10，

(4)

式中：F1为某个数据样本；Z1—Z10分别为不同公因子； 数字代表变量间的相关系数，数值越大时相关性越大。

2 基于PCA-TWSVM的故障监测与故障类型识别

2.1 基于PCA的故障检测

故障检测可以通过偏离程度的大小来实现，而PCA故障检测的建立需要2个统计量，即HotellingT2统计量(简称T2统计量)和平方预报误差(square prediction error，SPE)统计量。T2统计量的计算公式为

(5)

式中：Λ=diag(λ1,λ2,…,λk)为前k个主成分的特征值矩阵；yi为测试数据归一化后的样本向量；P为主成分模型的负荷矩阵。

T2统计量的控制限L为

(6)

式中：α为置信度；F(k,m-1),α为自由度为(k,m-1)的F分布临界值。

当置信度为α时，SPE统计量σSPE为

(7)

式中：I-PPT为残差子空间的投影；I为单位矩阵。

SPE统计量的控制限Q为

(8)

其中

(9)

(10)

式中cα为高斯分布水平是1-α的置信极限。

本文中选择T2统计量和SPE统计量都大于各自的控制限作为故障检测的标准。

2.2 基于TWSVM的故障类型识别

作为传统机器学习(SVM分支)的一种改进版本，TWSVM寻找的是一对不平行的超平面，因此具有更加优异的分类能力，非常适用于解决近似类型的样本分类问题[14-17]。此外，与传统SVM相比，TWSVM进行2个SVM型问题求解，因此计算效率更高。当样本个数为m时，标准SVM的时间复杂度约为O(m3)，而TWSVM时间复杂度为O[2(m/2)3]，计算时间约为标准SVM计算时间的1/4。

在实际应用案例中，大多数据样本都不是简单的二元分类。由于在故障数据特征空间中进行简单的线性TWSVM分类已经无法得到令人满意的分类结果，因此，对于非线性分类问题，即线性不可分时，需要引入核函数解决该问题。假设在n维实数空间n中，样本总数为m=m1+m2，其中m1为正类样本点个数，m2为负类样本点个数，那么寻求非线性TWSVM超平面的方法为

K(xT,CT)u1+b1=0,K(xT,CT)u2+b2=0 ，

(11)

式中：K为核函数, 采用高斯核径向基核函数作为TWSVM核函数；x为输入样本矩阵；C=(AB)T，其中A为由正类样本组成的m1×n型样本矩阵，B为由负类样本组成的m2×n型矩阵；u1、u2分别为正、负类样本的超平面法向量；b1、b2分别为正、负类样本的超平面偏移量。

同理，通过以下2个二次规划可以求解得到将正、负类样本划分开的平面[13-14]：

s.t.K(B,CT)u1+e2b1≥e2,

(12)

s.t.K(A,CT)u2+e1b2≥e1,

(13)

然后求解分类的超平面，采用的分类决策函数为

(14)

结合PCA方法，通过TWSVM对特征变量进行故障类型识别的具体实施步骤如图3所示。

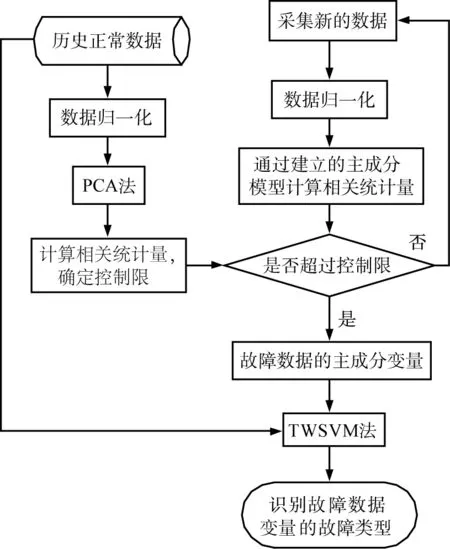
图3 基于主成分分析(PCA)-孪生支持向量机(TWSVM)的故障类型识别步骤

3 实验结果与分析

3.1 实验数据选取

为了验证本文中提出的PCA-TWSVM故障类型识别方法的性能，在MATLAB仿真平台利用加利福尼亚大学欧文分校(UCI)提出的用于机器学习的标准数据库UCI[15]进行验证分析。从UCI数据库中选取了隶属工业过程数据集中的Steel Plates Faults(钢板故障)数据集，共包含7类故障，特征维数为27。具体实验样本数据集参数见表1，其中随机选择了800个样本作为测试样本。实验过程中每一类样本的分类如表2所示。

表1 实验数据集参数

表2 样本分类情况

3.2 故障检测结果

由于本数据集的特征数较多，因此先利用 PCA方法对每个类别的数据样本进行降维处理，设置c大于或等于90%，计算出相应的主成分个数为9。最后计算出不同置信度时的T2统计量和SPE统计量结果，如图4所示。从图中可以看出：当置信度α=0.85、0.95时，有较多的正常数据存在错误判断； 当置信度α=0.99时，T2、SPE统计量的结果中超过控制限的数据均相对较少，因此，对于Steel Plates Faults数据集的故障检测，置信度α的最佳取值为0.99。后续结合PCA的TWSVM故障类型识别中，置信度α取值也为0.99。

(a)Hotelling T 2统计量

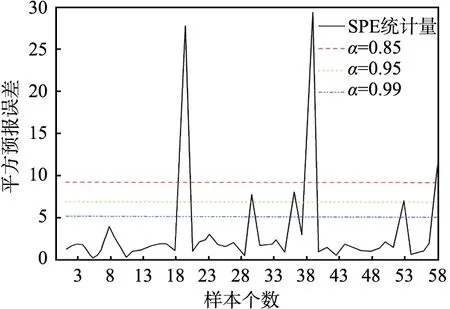
(b)SPE统计量图4 不同置信度α时的Hotelling T 2统计量和平方预报误差(SPE)统计量及控制限

3.3 故障类型识别

在上述PCA故障数据集降维处理之后，进行TWSVM故障类型识别实验，并且与现有的加权KNN[10]、PCA-KNN[11]和PCA-SVM[12]3种类型识别方法进行对比分析。为了验证方法的可行性，实验重复进行20次，测试样本与训练样本的设置见表2。4种方法的故障识别准确率如图5所示，综合性能对比见表3。从结果对比可以看出，相比于其他3种方法，本文中提出的PCA-TWSVM方法的识别效果最好，运行时间也有效缩短，对于故障类型识别具有更好的综合性能。

KNN—k邻近算法； PCA—主成分分析算法； SVM—支持向量机； TWSVM—孪生支持向量机。图5 不同方法的钢板故障识别的准确率

表3 不同方法对钢板故障类型的综合识别性能

4 结语

本文中提出利用PCA实现工业系统故障的检测，并使用TWSVM方法进行故障类型的识别。通过UCI数据库中的Steel Plates Faults数据集进行了实验测试，得出如下结论：相比加权KNN、PCA-KNN和PCA-SVM这3种方法，PCA-TWSVM方法在工业系统故障类型识别方面具有更高的准确率和执行效率。