基于二型模糊遗传控制器的冗余自由度机械臂运动控制的研究

屈海军，杨 森

（1.江苏安全技术职业学院机械工程学院，江苏徐州221011；2.辽宁工程技术大学材料学院，辽宁阜新123000）

在现代科技飞速发展的背景下，工业4.0越来越被人们所重视，工业机械化、自动化的程度得到了不断提升，给人们的工作和生活带来便利［1］。机械臂作为当下工业生产中重要的机械化与自动化相结合设备，已被人们应用于包含货物搬运、物流仓储以及设备制造等在内的多个生活领域［2-3］。机械臂的广泛应用，减轻了人们的劳动量，降低了人们在工作中的受伤风险。随着人们生活质量的不断提高，人们对机械臂运动控制的准确度要求也越来越高，期望通过控制其运动来实现一些精密的工作［4］。对此，人们展开了对机械臂运动控制的研究。

经过研究，当前出现了形式各异的机械臂运动控制方法。例如：Tenreiro 等［5］提出了一种基于分数阶微积分和分数阶矩阵幂的机械臂运动轨迹控制方法，将控制信号解释为沿轨迹规划系统传播的时空波，对其进行控制。文献［6］提出了一种tan型势垒lyapunov 函数来处理时变和迭代变化的约束要求，采用迭代学习控制更新律来学习迭代不变系统的不确定性，并采用鲁棒方法来补偿迭代和时变执行器的故障和干扰，以控制运动轨迹。文献［7］设计了一种中微子模糊PID控制器用于控制机械臂的运动轨迹，通过t（真）、i（不确定性）和f（假）隶属度函数确定先决变量的隶属度，进而实现对机械臂运动的控制。这些控制方法虽然能实现对机械臂进行运动控制，但在控制过程中的准确度和平稳度不高。

因此，本文在对冗余自由度机械臂进行动力学分析后，在二型隶属函数的基础上，定义了二型模糊集和区间二型模糊集，并利用其设计了区间二型模糊逻辑系统。通过区间二型模糊逻辑系统，构造了区间二型模糊PID 控制器，利用遗传算法选择其参数，以对机械臂的运动进行控制。为了验证所设计二型模糊遗传控制器的控制效果，采用其对锯齿和正弦目标轨迹进行跟踪，通过观察跟踪轨迹分析其控制效果。

1 冗余自由度机械臂的动力学分析

冗余自由度机械臂，是指具有比执行给定任务所需的额外自由度的机械臂［8］。这种冗余自由度是执行所需任务的一个重要特征，有助于提高其工作时的灵活度。图1 为具有旋转和棱柱冗余度的5自由度冗余机械臂结构［9］。

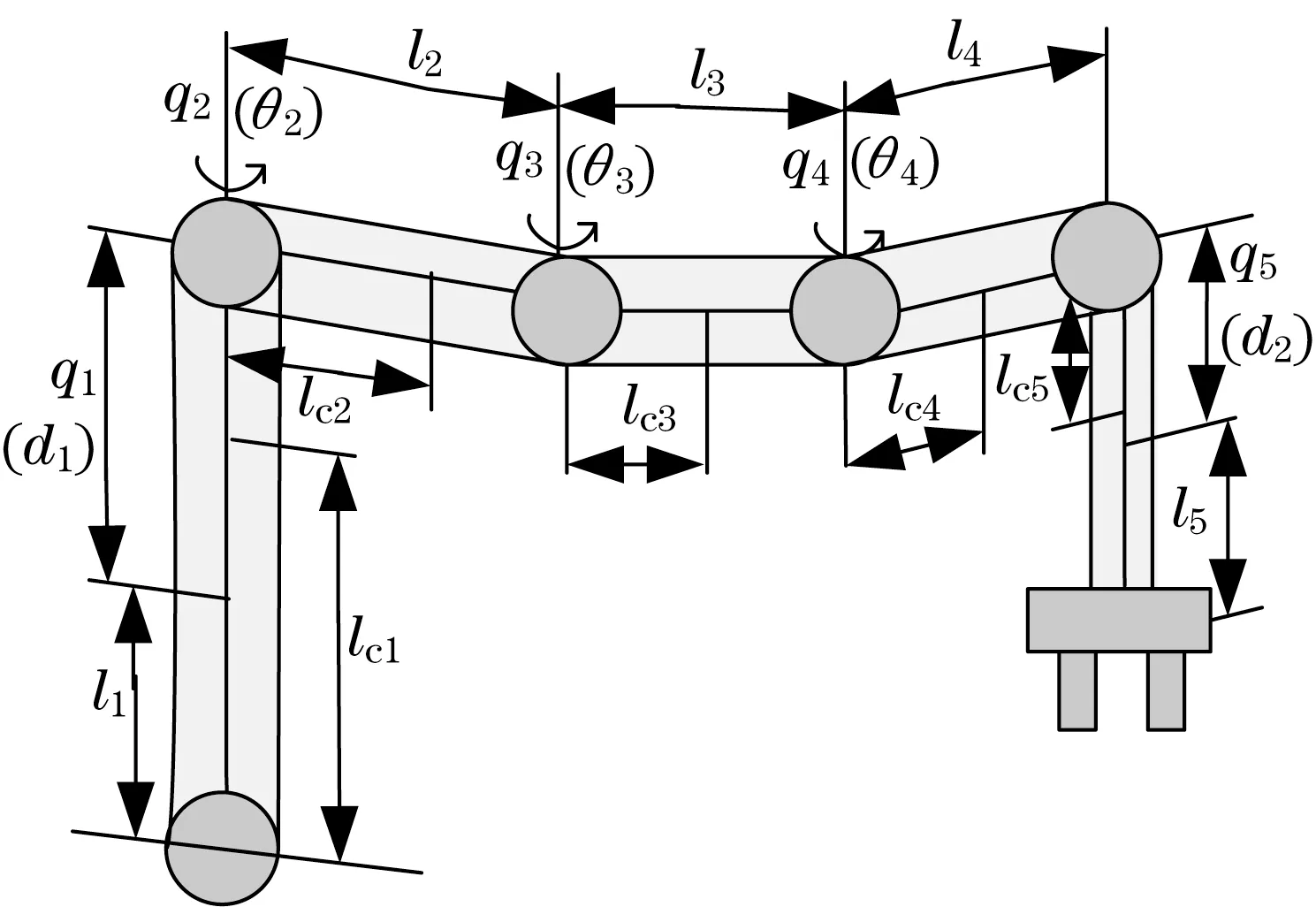
图1 具有旋转和棱柱冗余度的5自由度冗余机械臂示意图Fig.1 Schematic diagram of 5-DOF redundant manipulator having rotational and prismatic redundancy

从图1 可见，5 自由度机械臂具有p-r-r-r-p结构，即第 1 和第 5 关节为棱柱关节，而第 2、第 3 和第4 关节为旋转关节。棱柱关节沿垂直Z轴移动，而旋转关节在X-Y（水平）平面内移动。这保证了机械臂在Z轴上的柔顺性。

图中，机械臂在Z轴和水平平面上都有额外的连杆，使其成为了具有额外自由度的机械臂，因此，其属于冗余自由度机械臂的范畴；q1、q2、q3、q4、q5为位移d或角度θi（i=2，3，4）的广义坐标；l1、l2、l3、l4、l5为连杆长度；lc1、lc2、lc3和lc4分别是从质心到第 1、第2、第3 和第4 链路原点的长度。5 自由度冗余机械臂的链路变换为［10］

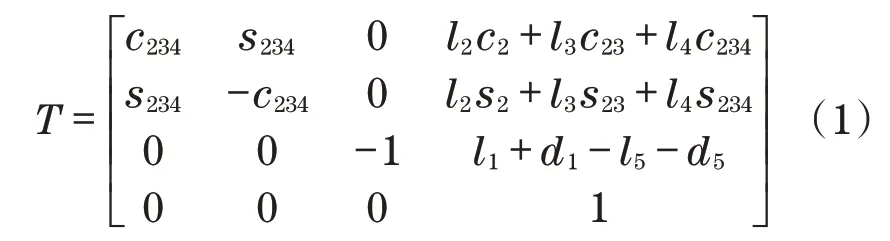
式 中 ：s2=sinθ2；s23=sin(θ2+θ3)；s234=sin(θ2+θ3+θ4)；c2=cosθ2；c23=cos(θ2+θ3)；c234=cos(θ2+θ3+θ4)。

通过式（1）可得出冗余机械臂的运动学方程为

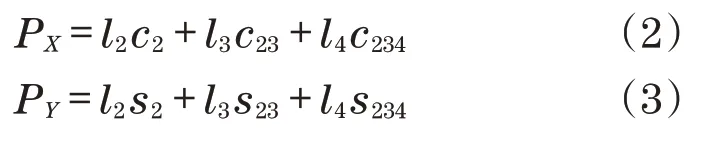
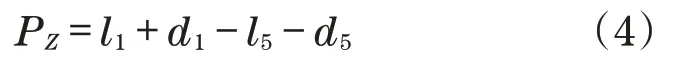
基于能量守恒原理的拉格朗日方程，是推导机械系统动力学模型的一种常用方法。拉格朗日函数为

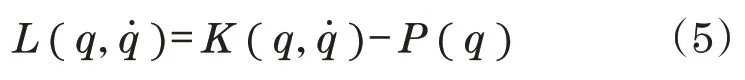
式中：拉格朗日函数值L为动能与势能P(q)之差。

为了确定机械臂系统的动力学方程，将拉格朗日函数代入欧拉-拉格朗日方程中可得

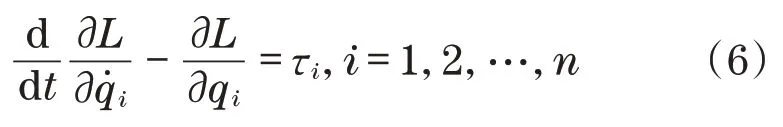
式中：qi为关节变量的广义位移或角度矢量为关节变量的广义速度矢量；τi为力或力矩的广义矢量。

修正拉格朗日方程后，可得冗余度机械臂扭矩与连杆位置关系的动力学模型

式中：τ为广义力矢量；M（q）为惯性矩阵为与科里奥利力矢量有关的矩阵分别为关节位置矢量、速度矢量和加速度的分量；G（q）为重力矢量为关节摩擦力矢量。

2 二型模糊遗传控制器的设计

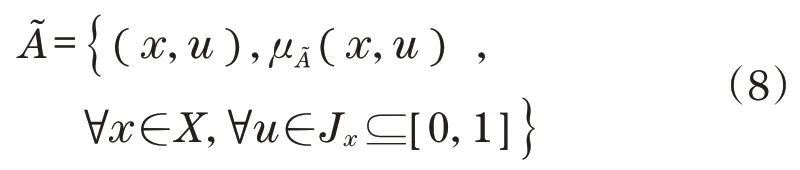
式中：x为主变量；在每个x∈X处，u为Jx中的次变量，次隶属函数的域为x的主隶属度；Jx为x的主隶属度。

(x，u)为次隶属度的振幅，(x，u)的支集可视为的不确定性足迹：

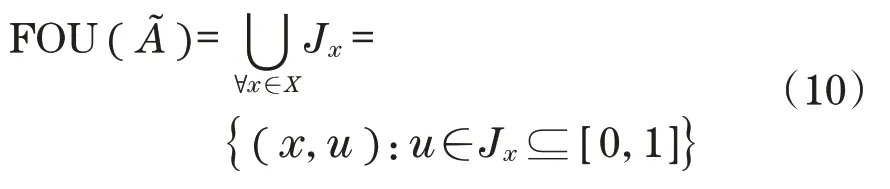
将FOU()用上隶属函数(x，u)和下隶属函数(x，u)为

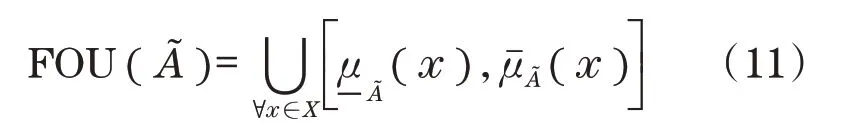
嵌入区间二型模糊集为

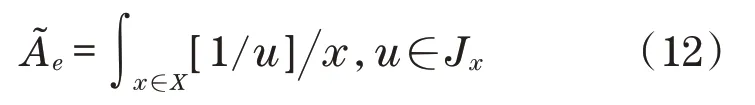
区间二型模糊逻辑系统由模糊化器、规则、推理机、解模糊器和减速机多个模块组成。在区间二型模糊逻辑系统中，输入和输出之间的映射可以表示为从精确输入到精确输出。

模糊化器用于将清晰的输入转换为0型、1型或区间二型模糊集。而在区间二型模糊逻辑系统中，有3种模糊化结果，即0型模糊化、1型模糊化和二型区间模糊化。通过模糊化器可将一个清晰的输入信息x=（x1，x2，…，xp）T转换为区间二型模糊集A~x。

区间二型模糊集A~x可视为多输入单输出量Ri的p维隶属函数：

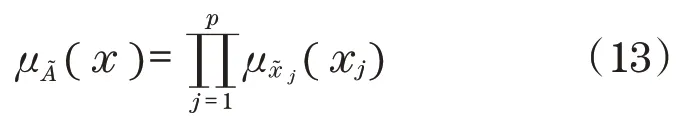
减速机是区间二型模糊逻辑系统输出处理的重要部分。一般二型模糊逻辑系统的质心计算较为困难，但区间二型模糊逻辑系统为了计算其质心，提出了一种迭代方法。区间二型模糊集的质心是区间一型模糊集，因此，计算质心将得到两个点，即左端点和右端点。

传统的时域PID控制器可以描述为［12］

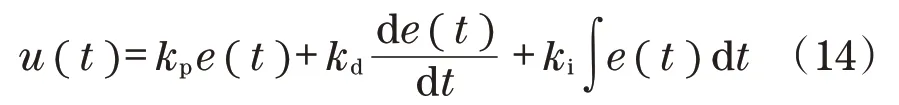
式中：kp、kd、ki分别为比例、微分、积分系数；e（t）为实际值与期望值之差。

传统PID 控制器具有含3 个输入和7 个隶属函数的规则库，可以得到7×7×7条规则［13］，即343。该规则库相当大，计算起来非常困难。因此，本文提出了如图2所示的区间二型模糊PID控制器。

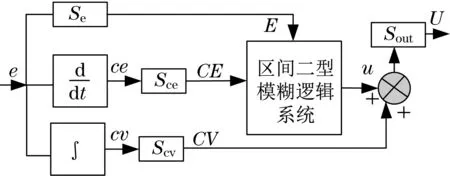
图2 区间二型模糊PID控制器框图Fig.2 Block diagram of interval two type fuzzy PID controller

由于高斯隶属函数是光滑的、在所有点上都是非零的非线性函数，因此，选择其作为区间二型模糊PID控制器的隶属函数。误差e、误差变化ce和控制输出cv，分别定义为期望关节矢量和实际生成关节矢量之间的差、误差信号的导数和误差信号的积分。e、ce和cv的话语域的最小值和最大值分别为－1和1。为了使控制器达到最佳性能，设计了如表1所示的规则库，用于区间二型模糊PID控制器。

本系统涉及物联网、大数据应用领域，是指一种基于物联网、大数据的室内微型健康环境监测分析系统。系统采用物联网技术对房间内外的温度、甲醛传感器、PM2.510数据进行识别、记录、存储，并形成房间内外环境数据分析报告和图例，实时获取居室环境情况。同时利用网络物联网服务器集数据采集、汇集为一体，可以独立记录单点居室数据，也可做为汇聚层收集多个居室，跨区域居室的数据，有效了解城市不同区域环境情况，提供环境大数据分析参考依据。未来还可以利用家居设备设施的智能化实现进行实时管理居室环境。

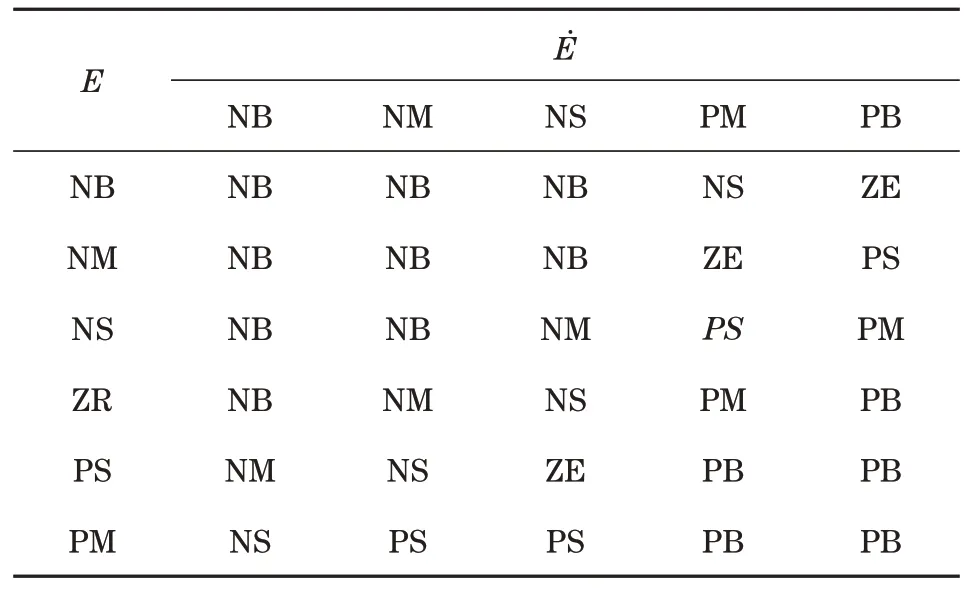
表1 区间二型模糊PID控制器的规则库Tab.1 Rule base of interval two type fuzzy PID controller

表1 中，用NB（负大）、NM（负中间值）、MS（负小）、ZE（零）、PS（正小）、PM（正中间值）和PB（正大）表示输入输出隶属度函数。

从图2 可见，区间二型模糊PID 控制器可视为一个关于三输入的函数：

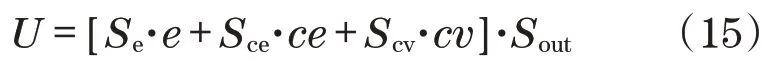
式中：Se、Sce、Scv为比例因子，初始值可通过遗传算法获取。

遗传算法是一种模拟人类基因进化的方法，其通过选择、交叉、变异3个过程来获取最优解［14］。

在选择阶段，个体i被选中的计算过程为

式中：fi为个体i的适应度值；n为种群中的个体总数。

完成交叉阶段后，遗传算法便进入变异阶段。在变异阶段通过计算变异概率px来提高其搜索能力，以获取最优解：

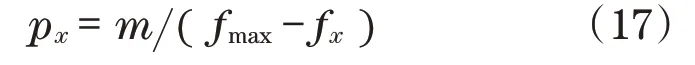
式中：m为（0，1）间的任意数；fmax、fx分别为最大适度值和变异个体x的适度值。

将区间二型模糊PID 控制器的比例因子视为遗传算法的初始群体，接着通过遗传算法的选择、交叉和变异3个阶段，便可获取最优值。

3 实验结果

采用Matlab/Simulink 作为仿真环境，对本文所设计的二型模糊遗传控制器（Two Type Fuzzy Genetic Controlle，TTFGC）及传统 PID 控制器（Traditional PID Controller，TPIDC）进行轨迹跟踪实验，以对TTFGC的控制性能进行验证。

3.1 锯齿轨迹跟踪

利用TPIDC 和TTFGC 对锯齿轨迹进行跟踪实验，通过观察其跟踪的实验结果，评价其对目标轨迹的跟踪效果。TPIDC 和TTFGC 对锯齿轨迹跟踪的实验结果如图3所示。

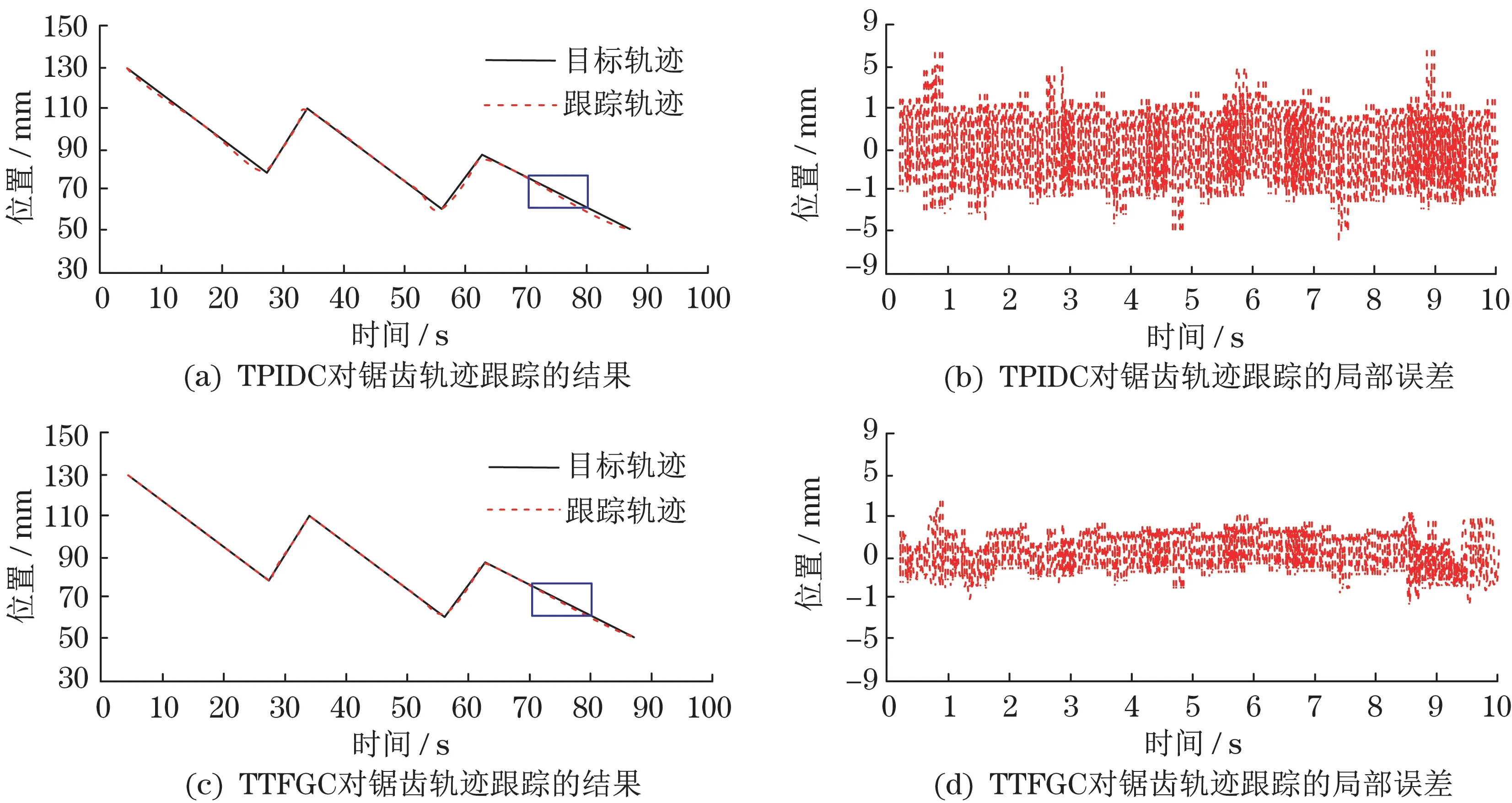
图3 不同方法对锯齿轨迹跟踪的结果Fig.3 Results of different methods for tracking sawtooth trajectory

通过观察图3（a）和图3（c）可见，TPIDC 和TTFGC 对锯齿轨迹的跟踪结果都还好。通过对比图3（b）和图3（d）可以发现：TTFGC 对锯齿轨迹跟踪的局部误差比TPIDC 对锯齿轨迹跟踪的局部误差小；而且在整个局部误差的观察过程中，TPIDC对锯齿轨迹跟踪的局部误差，比较TTFGC对锯齿轨迹跟踪的局部误差超调次数多，波动幅度也较大。在TPIDC 和TTFGC 对锯齿轨迹跟踪的局部误差中，其最大偏差分别为8.18 mm和2.21 mm。可见，TTFGC 对锯齿轨迹的跟踪效果比TPIDC 的跟踪效果好，整个跟踪过程更为稳定和准确。

3.2 正弦轨迹跟踪

TPIDC 和TTFGC 对正弦轨迹的跟踪结果如图4所示。

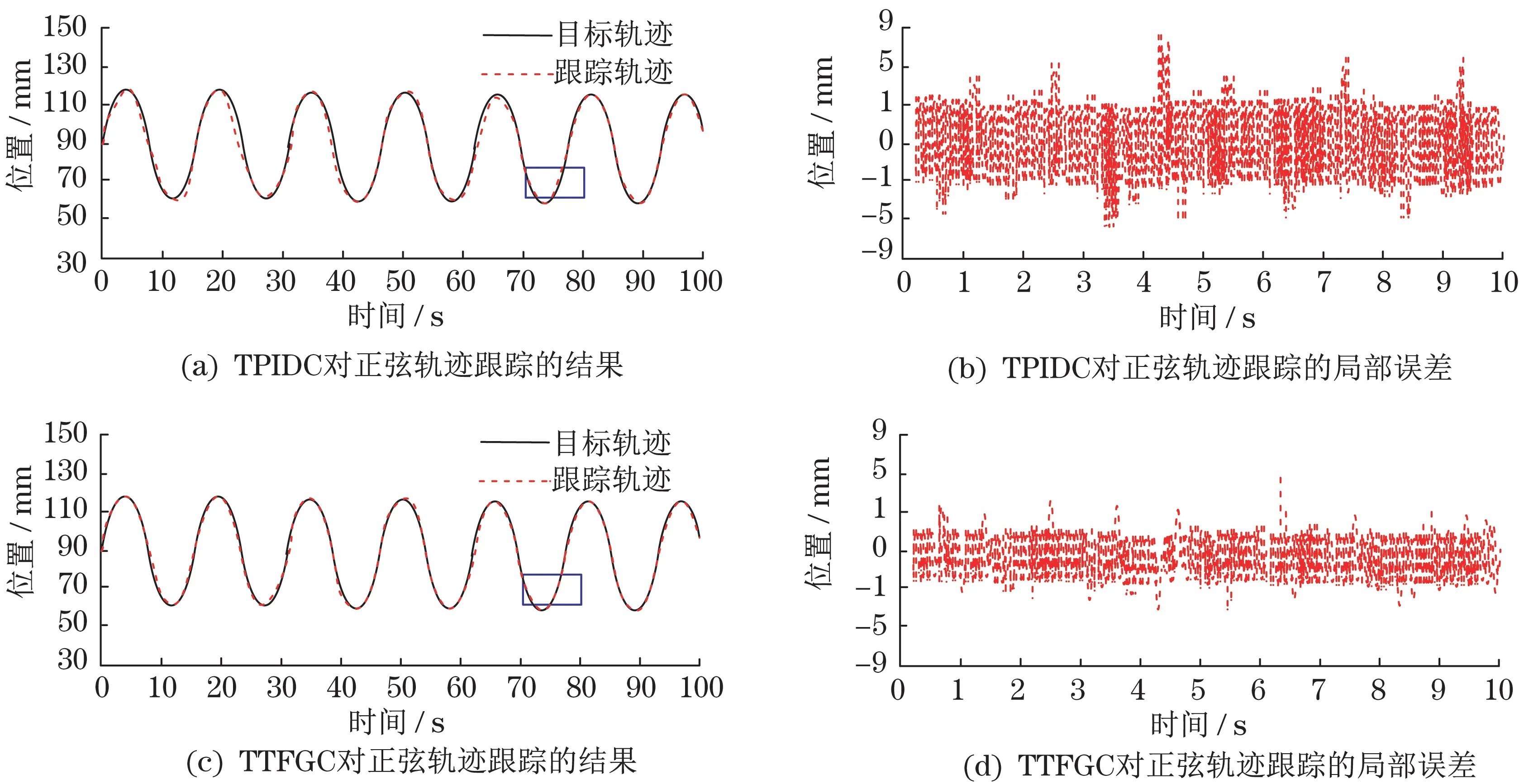
图4 不同方法对正弦轨迹跟踪的结果Fig.4 Results of different methods for tracking sinusoidal trajectory

对比两种方法对正弦轨迹的跟踪结果可以发现，其均能跟踪目标轨迹。但对各方法跟踪轨迹的局部误差进行比较可以发现，TTFGC 的跟踪误差比TPIDC 的跟踪误差更小，而且误差的波动程度也更小。在局部误差的观测时间内，TTFGC 的最大误差为4.98 mm，TPIDC的最大误差为8.64 mm。由此表明，TTFGC 能准确地跟踪正弦目标轨迹，而且跟踪误差较小，跟踪过程较为平稳。说明TTFGC 能够对冗余自由度机械臂进行更好的运动控制。

4 结语

通过对5 自由度冗余机械臂结构进行分析，明确5 自由度冗余机械臂的链路变换过程，得出冗余机械臂的运动学方程，进而建立冗余度机械臂的动力学模型。对二型模糊集及区间二型模糊集进行了定义，并在此基础上建立区间二型模糊逻辑系统。以区间二型模糊逻辑系统为依据，构建了区间二型模糊PID 控制器，并利用遗传算法选择参数，用以对冗余自由度机械臂的运动轨迹进行控制。通过二型模糊遗传控制器对锯齿目标轨迹以及正弦目标轨迹的跟踪结果表明：其能够控制冗余自由度机械臂较为准确、平稳地按照期望轨迹运动。