液压起重机轨迹跟踪控制方法的研究

范学慧 ，刘明明 ，2

（1.江苏建筑职业技术学院智能制造学院，江苏徐州221000；2.江苏大学机械工程学院，江苏镇江212013）

随着工业技术水平的不断提高，人们在多种工作场景中都需要对重物进行搬运等操作，此时起重机就发挥了其独特的优势［1］。液压起重机依靠其可控性好、工作效率高以及抗干扰能力强等特点，被人们广泛应用于房屋建筑、物流仓储以及林业种植等多个生活领域。正由于其在人们生活中的广泛应用，对其运动轨迹的控制进行研究就显得具有一定的实用价值［2-3］。

通过专家学者的研究，目前出现了一些液压起重机轨迹跟踪的方法。例如，Daniel 等［4］通过对轨迹规划算法和运动控制方法进行研究，设计了一种基于传感器测量跟踪参考轨迹的反馈控制器，用于控制液压起重机的运动轨迹。文献［5］中采用非线性模型预测控制实现协调动作，对液压起重机轨迹控制过程所需数值进行处理，从而使得目标函数最小化，以实现液压起重机的轨迹控制。Wu 等［6］设计了阻抗控制器，实现了负载的轨迹跟踪和阻抗调节，采用间接自适应鲁棒控制方法，在存在参数不确定性和未知干扰的情况下，使系统的跟踪性能达到最大，并获得二级控制单元的精确参数估计。虽然以上方法能够促进液压起重机的轨迹控制效果，提高液压起重机对目标轨迹的跟踪正确度，但是，由于这些方法没有考虑系统中的死区补偿以及前馈信号控制，使得这些方法控制液压起重机对目标轨迹跟踪时，跟踪正确性不够高，存在较大的波动和误差。

对此，本文通过分析液压起重机的结构，建立了其旋转关节和执行机构的运动学模型。引入一个正弦波信号，建立了死去补偿装置模型，将气缸开始移动的位置（输出行程和输入行程）与输入正弦波进行比较，以补偿死区信号；并通过液压起重机的频率响应函数，求取前馈信号增益，以控制液压起重机对目标轨迹的跟踪。为了验证本文方法的有效性，利用本文方法对矩形目标轨迹、圆形目标轨迹以及三角形目标轨迹进行了跟踪测试，通过观察测试曲线以分析本文方法的控制效果。

1 液压起重机分析

图1 为转向节臂式液压起重机，其具有3 个旋转关节和1 个伸缩关节。液压起重机的第2 和第3个水平旋转关节，提供了起重机在x与z轴上的笛卡尔操作［7-8］。

图1 液压起重机Fig.1 Hydraulic crane

通过Denavit-Hartenberg 方法可以求取负载的位置方程［9］为

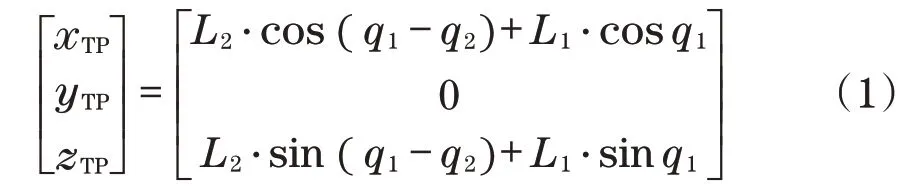
式中：xTP、yTP、zTP分别为负载在x、y、z3个轴向上的位置；L1、L2分别为第2 和第3 个水平旋转关节的长度；q1为第 2 旋转关节与x轴的夹角；q2为第 3 个水平旋转关节与第2旋转关节的夹角。

从式（1）可见，负载在y轴上的位置为0，因此，在对液压起重机的运动学分析时可忽略其y轴信息。

第 2 和第 3 个水平旋转关节的角速度为q˙1和q˙2，可通过xTP、zTP计算而得到，方程为

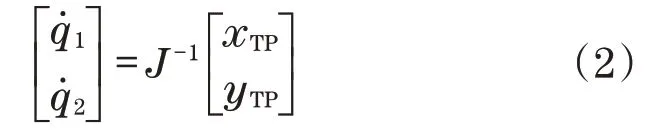
式中：J-1为逆雅可比矩阵，其表达式为

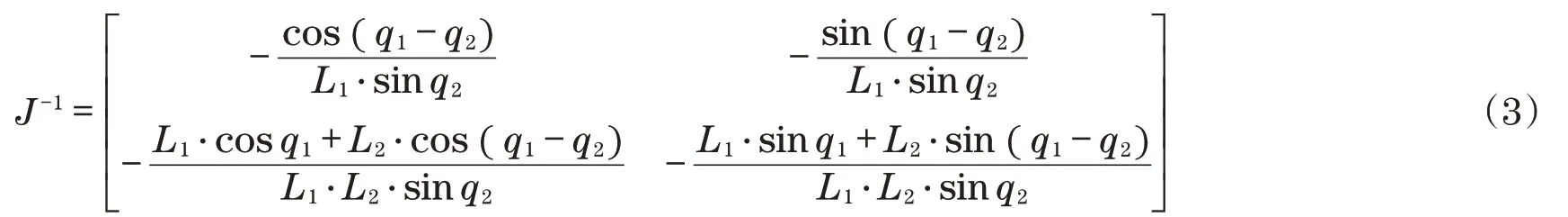
根据起重机的逆运动学方法，通过q2的正弦值以及余弦值求取其正切值，在对正切值求取反变换，即可获取q2的值为

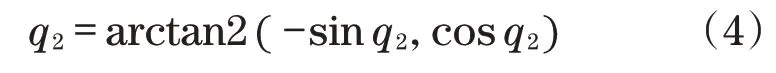
获取q2后，可将其联合L1、L2来求取q1的值为

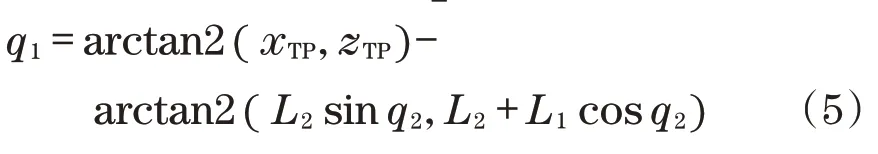
接头的旋转由液压执行器驱动。气缸行程函数的关节角度值是一个特定于结构的几何映射，其测量了起重机接头之间的距离。

采用曲线拟合的方法将气缸活塞行程表示为关节角度的函数，从而获得直接作动器运动学。首先，利用逆执行器映射对操作点进行等距采样；然后，将输入和输出数据转换为采样数据，从而为直接执行器运动学的曲线拟合提供了样本数据。气缸行程p拟合为连接角q的多项式函数可表示为

式中：N为拟合给定采样数据时的多项式总数；K为多项式系数，其可通过Matlab 的数值曲线拟合工具箱确定［10］。

利用链式法则，对式（6）进行计算，以求取执行机构的速度值p˙［11］为

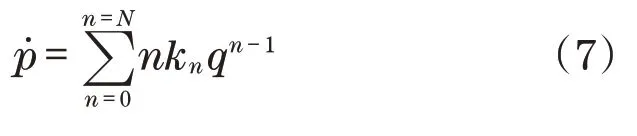
2 控制系统设计

本文设计的液压起重机控制系统的框图如图2所示。

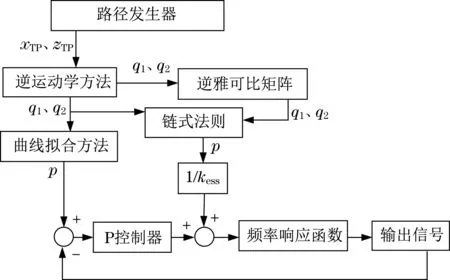
图2 液压起重机控制系统框图Fig.2 Block diagram of hydraulic crane control system

图2 表达了控制信号从路径发生器到气缸活塞行程和速度变化的完整信号流。图中，控制系统的输入端是一个路径发生器，它在笛卡尔空间中提供一个具有负载位置和速度的时间序列。控制系统通过起重机的逆运动学方法，得到起重机的关节角作为负载位置的函数。通过起重机的正向运动学方法，求取前馈控制信号所需要的逆雅可比方程。

由于液压起重机中两个气缸的方向控制阀是重叠阀，因此，输入端存在非线性的固有死区。本文通过引入一个相对低频的正弦波来发现死区，将气缸开始移动的位置（输出行程和输入行程）与输入正弦波进行比较，以补偿死区信号。由此可得死区补偿装置的模型为

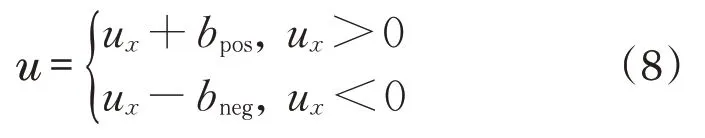
式中：u为进入控制阀的控制信号；bpos、bneg分别为输入信号ux的正和负时，气缸开始移动的位置。

由于起重机的非线性特性，当施加多个周期的正弦波时，气缸行程值将会产生漂移。此时，可利用输入信号减去其导数平均值的线斜率，以消除测量数据的漂移。消除测量数据的漂移后，可从每次测量值中准确地提取出测量值振幅和相位，以求取测量的频率响应函数。通过该方法可得液压起重机的频率响应函数为

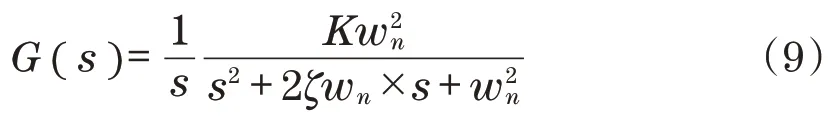
式中：s为输入信号的频域值；K为稳态增益；ζ为阻尼比；wn为固有频率。

利用式（9）可求取下执行器的传递函数GL（s）和上执行器的传递函数GU（s）为

利用式（9）可计算出图2 中前馈信号的反向稳态增益kess为

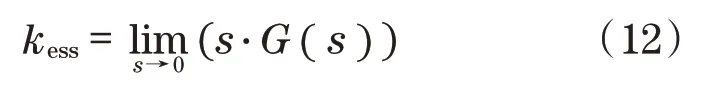
联合式（10）～式（12），可求出下执行器的前馈增益值kessL和下执行器的前馈增益值kessU分别为

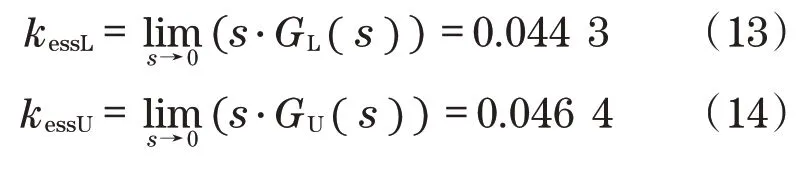
3 实验结果

以 Intel I3 双核 CPU、4 GB 内存的 Lenovo 计算机上作为实验平台，通过Matlab/Simulink 作为实验软件，对本文所设计方法的轨迹跟踪效果进行实验测试。测试中采用了神经网络控制方法作为对比，更为直观地观察本文方法的轨迹跟踪优越性。实验中设置了多种目标轨迹，通过对本文方法和神经网络方法的跟踪轨迹进行观察，以分析不同方法的轨迹跟踪性能。

3.1 矩形目标轨迹跟踪测试

通过设定一个矩形目标轨迹，利用本文方法和神经网络方法对该目标轨迹进行跟踪。两种方法的对矩形目标轨迹的跟踪结果如图3所示。

通过观察图3 中两种方法对矩形目标轨迹的跟踪曲线，可以发现，神经网络方法的跟踪轨迹中存在较多的波动，而且跟踪轨迹相对目标轨迹产生偏移时，需要调整更久才能再次贴合目标轨迹。神经网络方法的跟踪轨迹中，与目标轨迹的最大偏差度为14.81%。本文方法的跟踪轨迹波动次数较小，而且产生偏移时，能够较快地再次贴合目标轨迹。本文方法的跟踪轨迹中，与目标轨迹的最大偏差度为9.33%。由此说明，本文方法能够较好地跟踪矩形目标轨迹，跟踪过程中出现的波动次数较少。

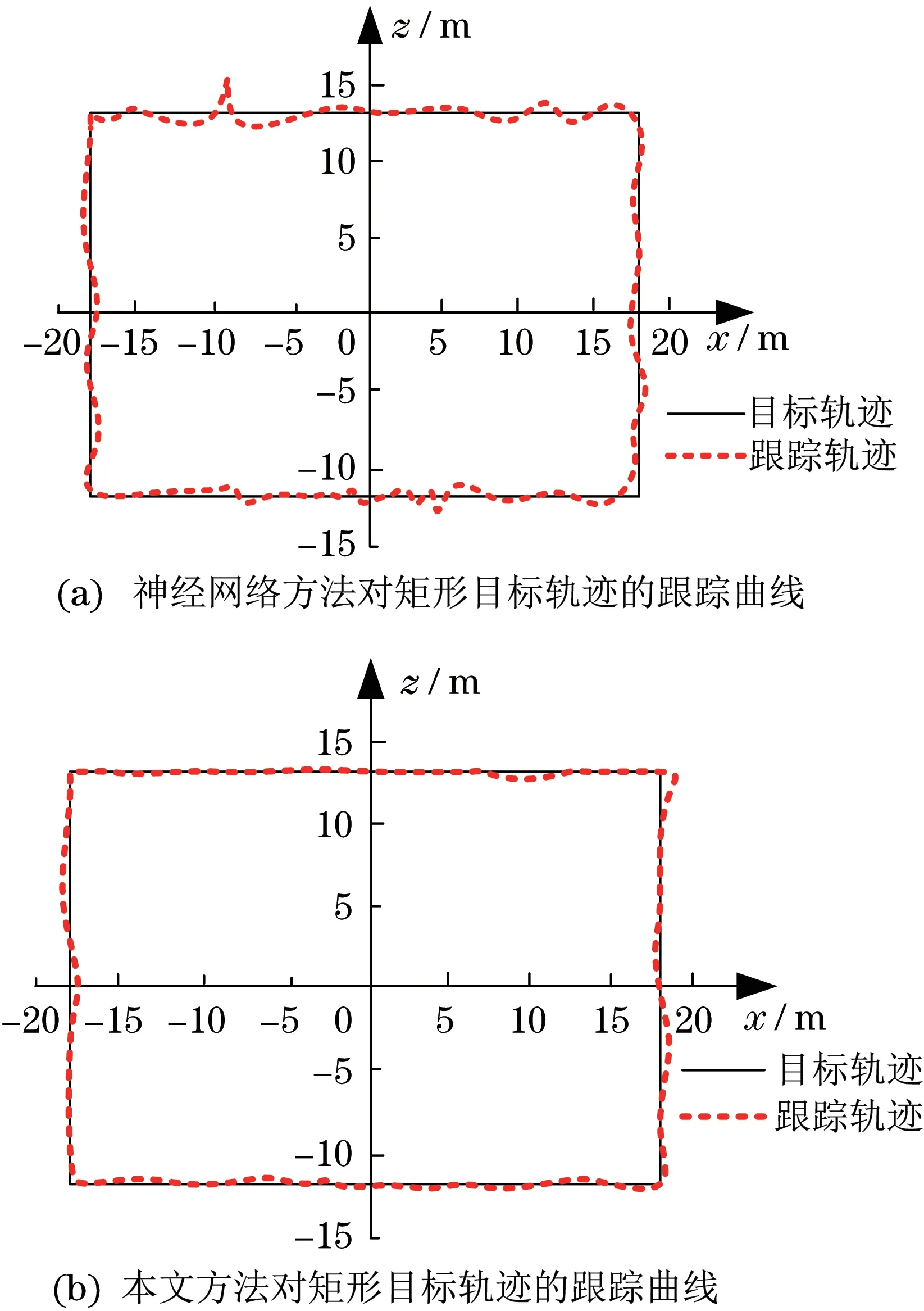
图3 不同方法对矩形目标轨迹的跟踪结果Fig.3 Tracking results of rectangular target trajectories by different methods

3.2 圆形目标轨迹跟踪测试

图4 显示了不同方法对圆形目标轨迹的跟踪结果。

如图4 可见，与神经网络方法对圆形目标轨迹的跟踪曲线相比，本文方法对圆形目标轨迹的跟踪曲线更为平滑，出现波动的次数更少。在对圆形目标轨迹跟踪时，神经网络方法的跟踪轨迹中，与目标轨迹的最大偏差度为32.26%。本文方法的跟踪轨迹中，与目标轨迹的最大偏差度为12.5%。说明，与神经网络方法相比，本文方法能够更好地对圆形目标轨迹进行跟踪。

3.3 三角形目标轨迹跟踪测试

神经网络方法与本文方法对三角形目标轨迹的跟踪结果，如图5所示。

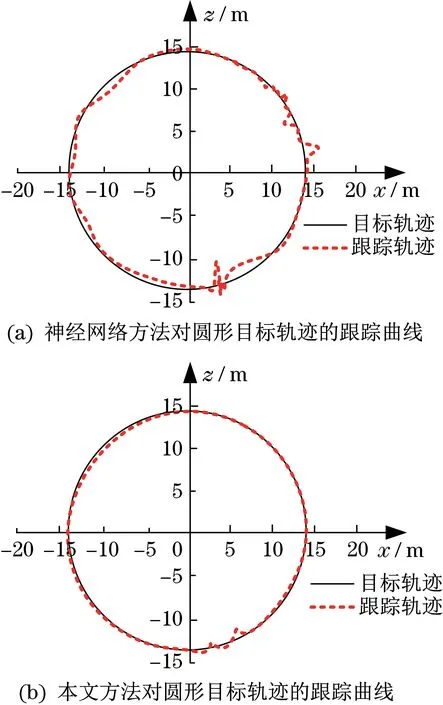
图4 不同方法对圆形目标轨迹的跟踪结果Fig.4 Tracking results of circular target trajectories by different methods

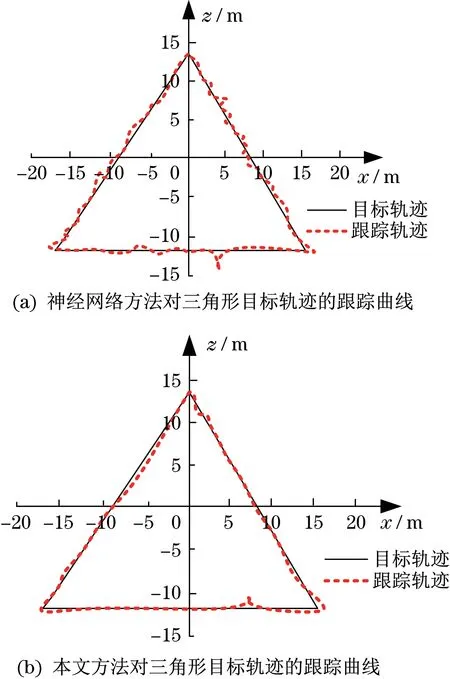
图5 不同方法对三角形目标轨迹的跟踪结果Fig.5 Tracking results of triangular target trajectories by different methods

图5 中，神经网络方法在对三角形目标轨迹进行跟踪时，平稳度不高，产生波动的次数较多。整个跟踪过程中，神经网络方法的跟踪曲线出现了多次较大的波动，与目标轨迹相比，其跟踪曲线中产生的最大偏差度为26.07%。而本文方法对三角形目标轨迹进行跟踪时，平稳度较高，产生波动的次数较少。与目标轨迹相比，本文方法的跟踪曲线中产生的最大偏差度为8.70%。可以看出，本文方法能够较好地跟踪三角形目标轨迹。说明本文方法有助于提高液压起重机对目标轨迹的跟踪正确度，使得液压起重机能够更为平稳、准确地按照目标轨迹进行工作

4 结语

本文针对具有笛卡尔轨迹跟踪任务的液压起重机，设计了一种轨迹跟踪控制方法。在对液压起重机分析的基础上，推导了其关节角速度以及执行机构的速度模型。引入一个相对低频的正弦波，构造了死区补偿装置模型。并通过液压起重机的频率响应函数，计算了前馈信号的反向稳态增益。通过观察本文方法对矩形目标轨迹、圆形目标轨迹以及三角形目标轨迹的跟踪曲线，分析了本文方法的跟踪性能。通过本文方法的跟踪曲线，本文方法不仅有助于提高液压起重机对目标轨迹的跟踪正确度，而且还能保证液压起重机对目标轨迹跟踪过程的平稳性。