等高线法的桥式起重机主梁损伤识别

范小宁，罗志宏

（太原科技大学机械工程学院，山西太原030024）

起重机作为一种现代化工业中重要的物料搬运机械，广泛应用于机械制造、钢铁冶金及铁路交通等部门和场所，在重工业行业里起着非常重要的作用。起重机金属结构是起重机的机械骨架，起着承受起重机的自重及其载重的作用，是起重机的重要部件，决定着起重机的寿命。起重机金属结构属于焊接件，其一投入使用就不可避免地存在有夹渣、气孔等焊接缺陷，再加上起重机所受冲击载荷的长期作用及环境腐蚀和老化的影响，常常会出现疲劳裂纹损伤。当损伤累积到一定的程度就会引起突发性的结构断裂，从而引发重大事故和经济损失。因此，对起重机金属结构的早期裂纹损伤识别研究具有重要意义。

由于结构的损伤必然会引起结构模态频率和振型等模态参数的改变，因此，基于模态的损伤识别分析是一种经济高效的结构无损检测技术［1］。基于模态的损伤识别方法主要有以下几种：基于固有频率的损伤识别方法、基于柔度的损伤识别方法、基于曲率模态的损伤识别方法、基于振型的损伤识别方法等［2］。文献［3］在考虑裂纹梁刚度随振幅变化的基础上，结合等高线裂纹识别方法与理论，利用固有频率对试验用呼吸式裂纹悬臂梁进行损伤识别研究。文献［4］利用固有频率方法对单裂纹单吊点矩形截面试验用悬臂梁进行了损伤识别。基于固有频率的等高线法量测精度高，无需多点测量，即使测量系统存在一定误差，仍可给出满足工程需要的损伤识别结果，而且方法简单，容易应用于工程实践。目前，基于模态频率进行损伤识别的研究主要集中于一些试验用悬臂梁结构，用于实际机械结构损伤的研究还很少。为此，本文以ANSYS 为软件平台，通过对桥机主梁的模态分析，应用等高线法进行了起重机金属结构的损伤识别研究，并取得了满意的识别效果。

1 基于模态频率损伤诊断理论

结构的振动特性反映了结构的固有特性，是研究其他动力问题的基础，结构的振动特性分析也称模态分析，一般包括频率和振型的计算，整个起重机的结构有限元动力方程为

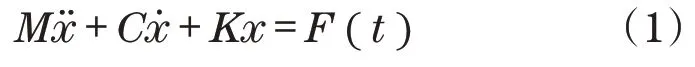
式中：M、C、K、F(t)分别为桥式起重机结构的质量矩阵、阻尼矩阵、刚度矩阵和外荷载向量分别为加速度向量、速度向量和位移向量。

式（1）中，如果结构的阻尼矩阵C和外荷载向量F(t)均为0，则这类振动称为无阻尼自由振动。解无阻尼自由振动方程，可以得到结构的无阻尼自由振动频率和振型。

无阻尼自由振动方程为

由式（2）可得存在裂纹情况下固有振动特征方程为

为进行起重机主梁振动模态分析，引入梁单元内的势能泛函［5］

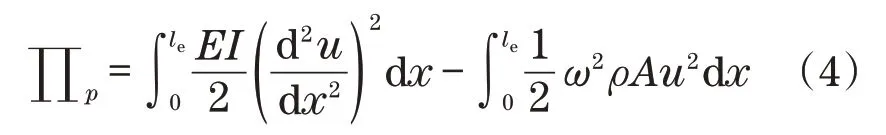
式中：u为梁挠度；EI为梁抗弯刚度；le为单元长度；ρ为密度；A为梁截面面积；ω为振动频率。

单元内挠度函数ue的插值表示如下：

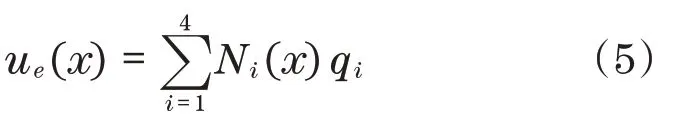
式中：N(x)为梁单元的形函数Ni(x)组成的向量；qe为单元节点坐标qi组成的向量。

单元形函数是以下形式的三次多项式：

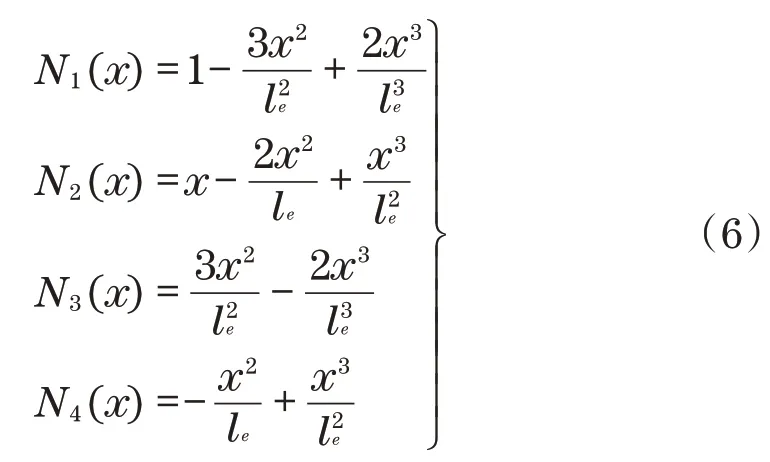
将单元挠度插值式（5）代入总势能式（4）中，得到

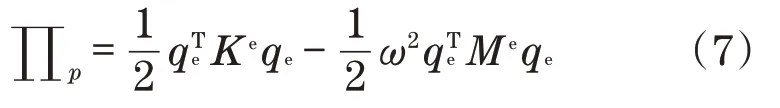
根据最小势能原理可以得到单元内振动模态方程

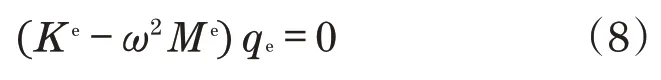
式中：Ke为单元刚度矩阵；Me为单元质量矩阵，其表达式为

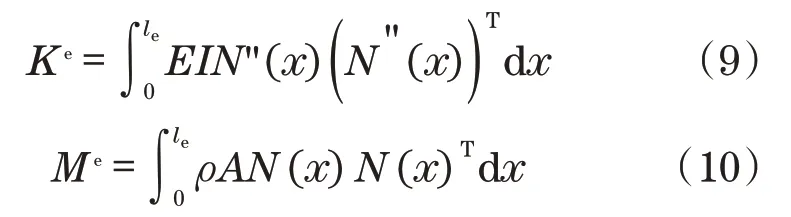
由于单元形函数式（6）具有明确表达式，则式（9）和式（10）的积分很容易求解。

对于整个结构，总体刚度矩阵K、质量矩阵M可由单元刚度矩阵和单元质量矩阵的叠加得到。则由式（3）可以得到桥机主梁各阶固有频率ωr(r=1，2，…，n)。

2 裂纹识别方法与理论

如果定义由裂纹位置和损伤程度确定固有频率称为正问题，那么由固有频率识别裂纹位置和程度则称为逆问题。基于固有频率方程，对应于不同的裂纹位置和裂纹长度，可以得到各阶次固有频率。同样，如果已知桥式起重机的固有频率，也可以由已知的固有频率与裂纹位置和长度的关系式，求解出裂纹的位置和长度。桥式起重机的固有频率方程是考虑了裂纹位置、裂纹长度二元函数。从求解线性方程组的角度来看，通过固有频率识别裂纹位置、裂纹长度，只需知道两阶固有频率就可以求得唯一解。为了避免振动测量中的节点效应［6］并考虑工程测试中高阶模态频率误差相对较大的实情，取前三阶固有频率的实测值进行损伤识别。

结合起重机的固有频率方程和刚度模型，基于等高线法可识别出裂纹位置和损伤程度，其识别过程为：首先，拟合出以裂纹位置和损伤程度为自变量的固有频率响应面；然后，将实测固有频率代入到频率响应面上，得到若干条频率等高线并投影到同一平面，等高线理论上必然存在一个交点，这个交点横纵坐标即对应裂纹位置和裂纹损伤程度［3］。

3 算例分析

本文基于ANSYS 有限元分析软件平台，采用APDL 语言对桥式起重机进行了参数化有限元建模，其有限元模型如图1 所示。该起重机的起质量为32 t，大车跨度L=31.5 m，单元设置为SHELL63弹性壳单元。

材料属性为：弹性模量E=2.12×1011N/m2，泊松比μ=0.358 8，密度ρ=7.86×103kg/m-3。

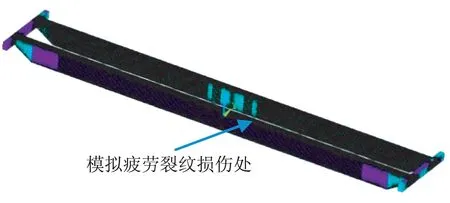
图1 桥式起重机有限元模型图Fig.1 Finite element model of bridge crane

根据理论分析和实际使用情况，发现起重机主梁中部是其疲劳裂纹萌生、扩展和易损区，因此，有限元分析在主梁中部位置腹板下部附近处沿纵向模拟添加疲劳裂纹。带疲劳裂纹的主梁中部腹板的局部放大图如图2所示。

图2 主梁中部腹板处带裂纹的局部放大图Fig.2 Partial enlarged drawing with cracks at the middle web of main beam

根据基于断裂力学理论的起重机金属结构疲劳寿命研究［7］，定义100 mm 为起重机主梁的临界裂纹尺寸，此时起重机不能再使用。这里分别按照临界裂纹尺寸的10%～90%（即主梁疲劳损伤程度）进行带疲劳裂纹主梁的模态分析。表1～表3 为对应不同裂纹位置和损伤程度的起重机主梁前三阶的模态频率。

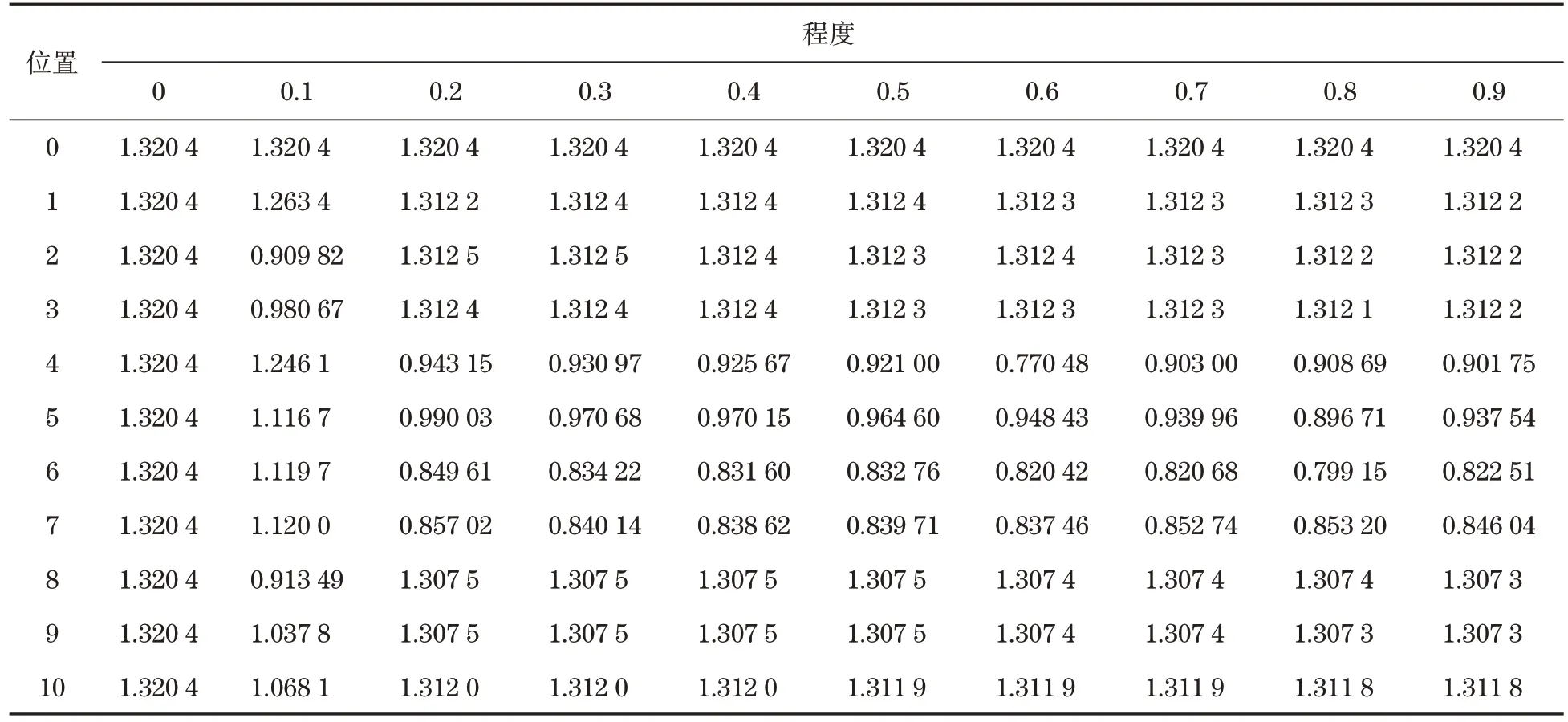
表1 一阶模态频率Tab.1 The first mode frequency

然后，利用曲面拟合技术对表1～表3的样本进行曲面拟合，获得损伤工况对应前三阶起重机主梁固有模态频率的响应曲面如图3～图5所示。

考虑裂纹位置和裂纹损伤程度的频率响应曲面，设计出6 种不同的裂纹损伤工况，验证等高线相交损伤识别方法的有效性。

把表4 中各种损伤工况条件下的前三阶固有频率代入含裂纹起重机固有频率响应面，可得到对应的固有频率等高线，将等高线投影到水平面，得到对应损伤工况的裂纹位置和损伤程度的关系曲线。

工况1：将一阶模态频率z=0.990 03 代入图3一阶裂纹模态频率响应面，得到对应的模态频率等高线，将等高线投影到水平面xOy内，得到图6 的线1；将二阶模态频率z=1.671 5 代入图4 二阶裂纹模态频率响应面，得到对应的模态频率等高线，将等高线投影到水平面xOy内，得到图6的线2；将三阶模态频率z=1.739 1 代入图5 三阶裂纹模态频率响应面，得到对应的模态频率等高线，将等高线投影到水平面xOy内，得到图6 的线3；线1、2、3 相交一点，该交叉点的纵横坐标即为损伤工况1 的损伤位置和损伤程度。

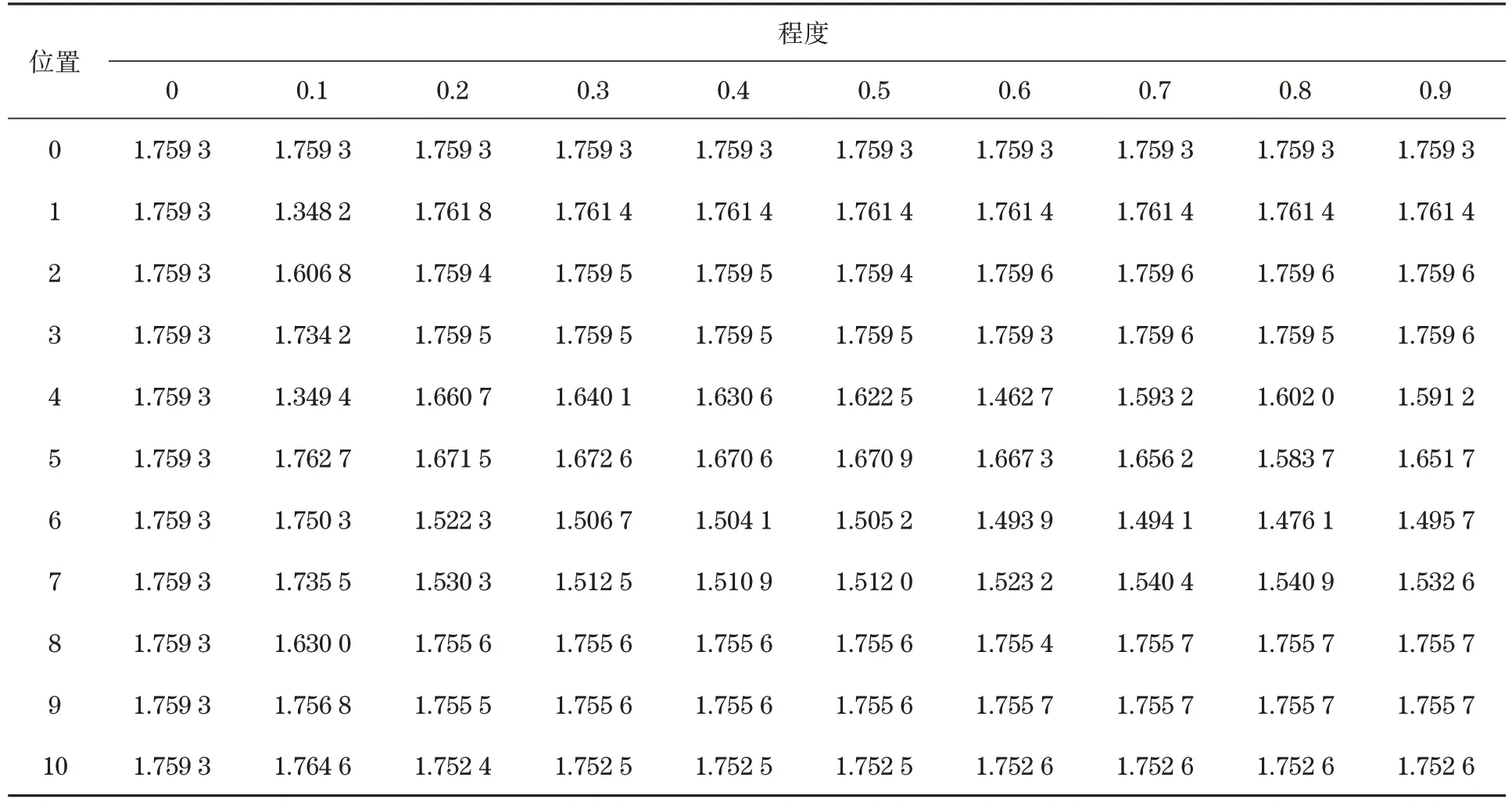
表2 二阶模态频率Tab.2 The second mode frequency

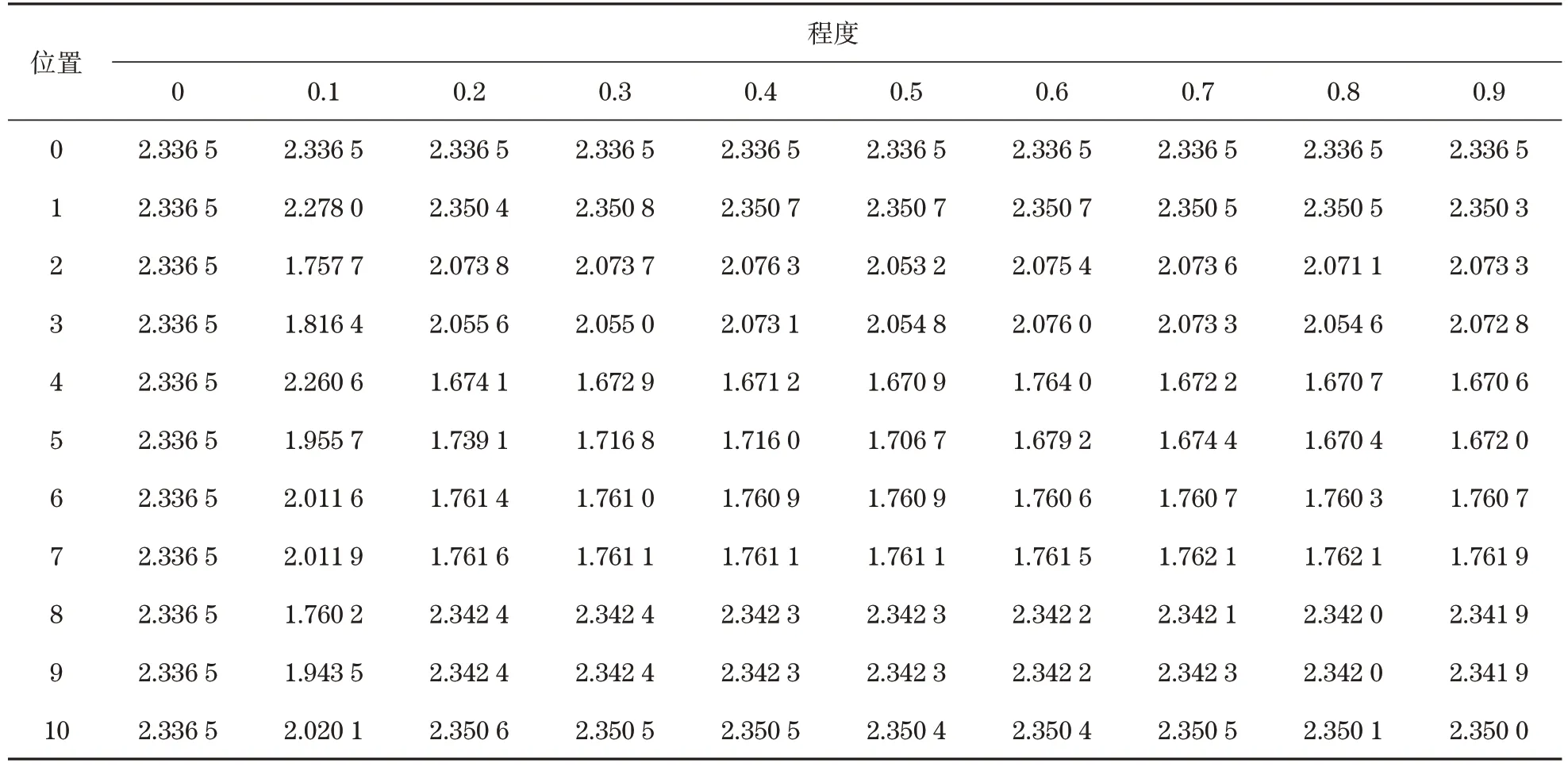
表3 三阶模态频率Tab.3 The third mode frequency

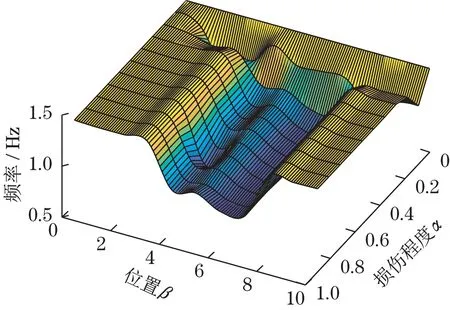
图3 一阶模态频率Fig.3 The first mode frequency

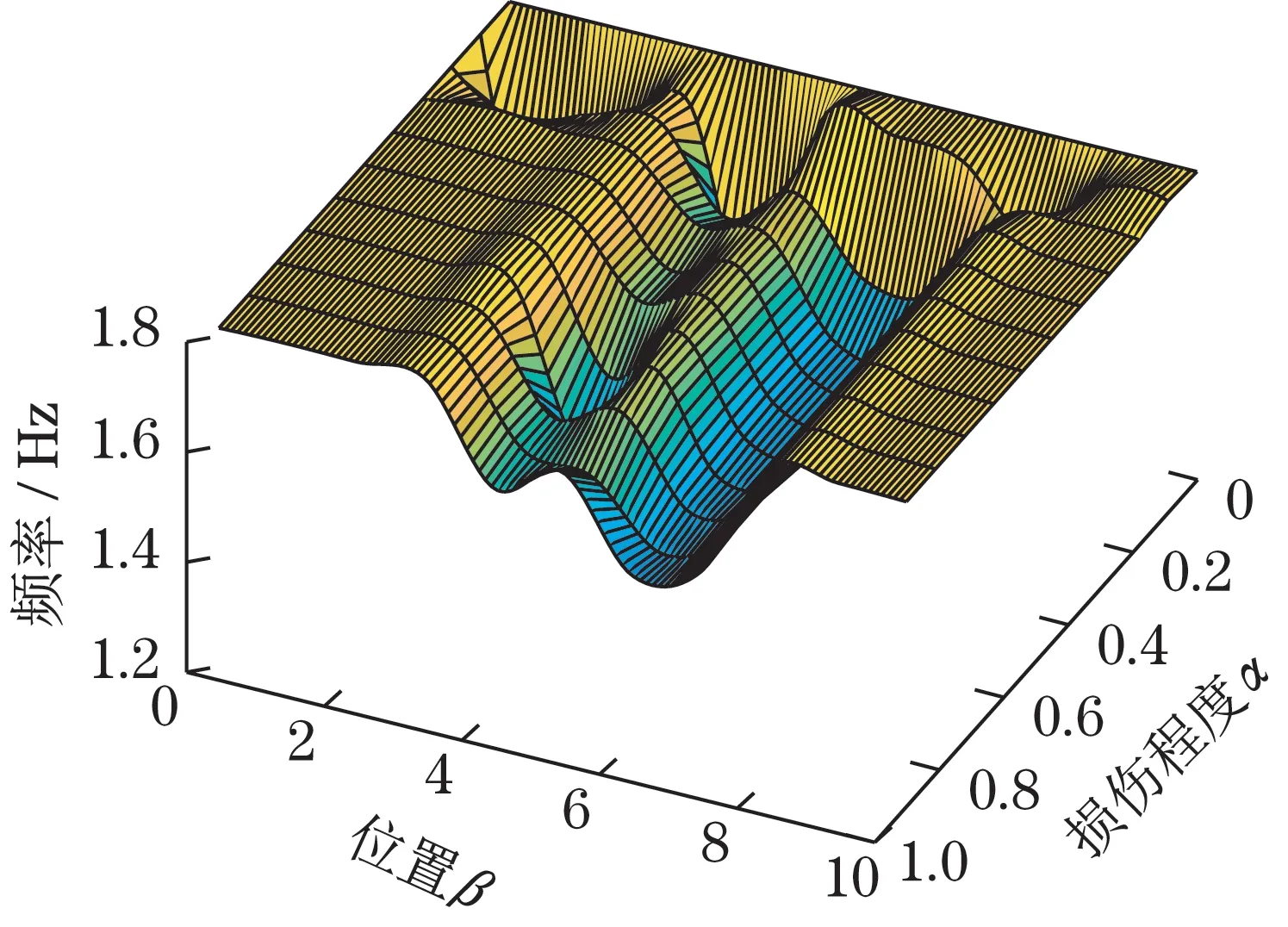
图4 二阶模态频率Fig.4 The second mode frequency

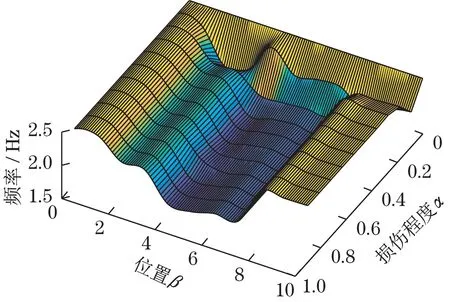
图5 三阶模态频率Fig.5 The third mode frequency

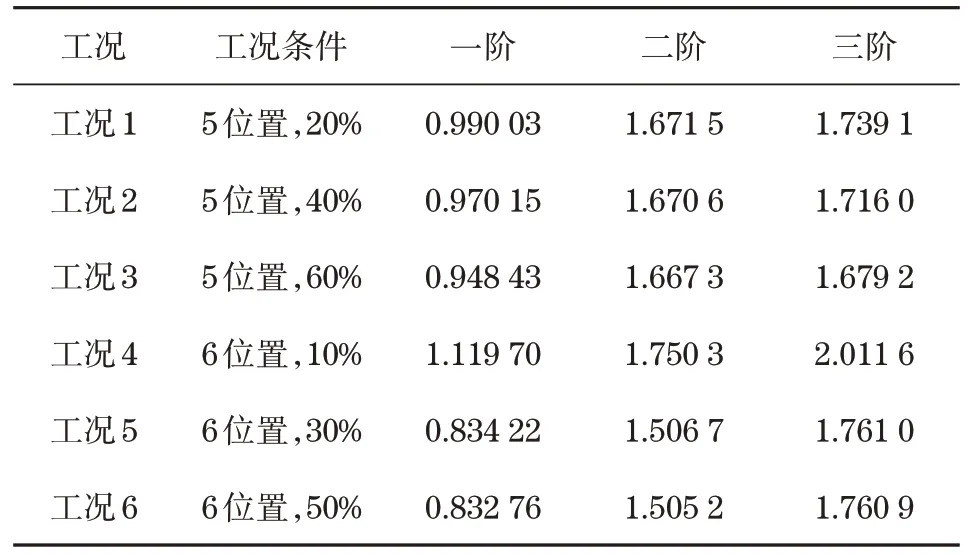
表4 不同裂纹条件下的前三阶模态频率Tab.4 The first three modal frequencies under different crack conditions

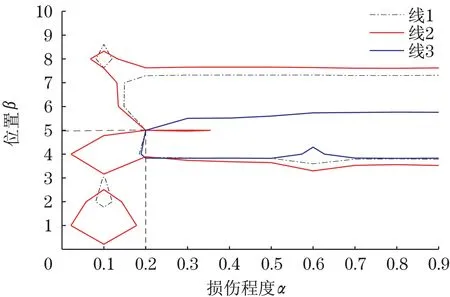
图6 工况1Fig.6 Working condition1

同理可得到对应损伤工况2～6 的等高线交叉点，如图7～图11。从图中可以看出，各交叉点的纵横坐标分别对应各损伤工况的损伤位置和损伤程度，因而应用等高线法可以非常方便地获得裂纹的损伤参数，实现裂纹的损伤识别。

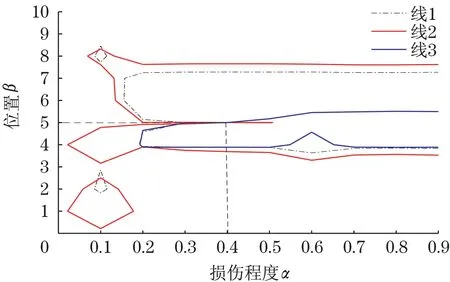
图7 工况2Fig.7 Working condition 2

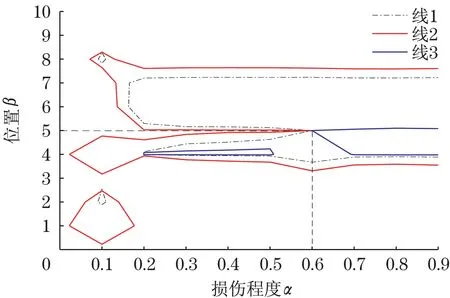
图8 工况3Fig.8 Working condition 3

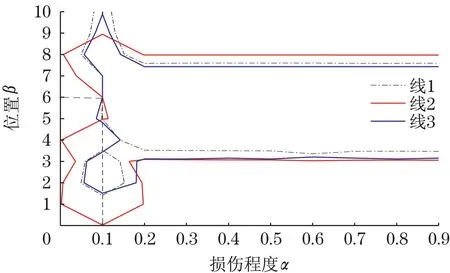
图9 工况4Fig.9 Working condition 4

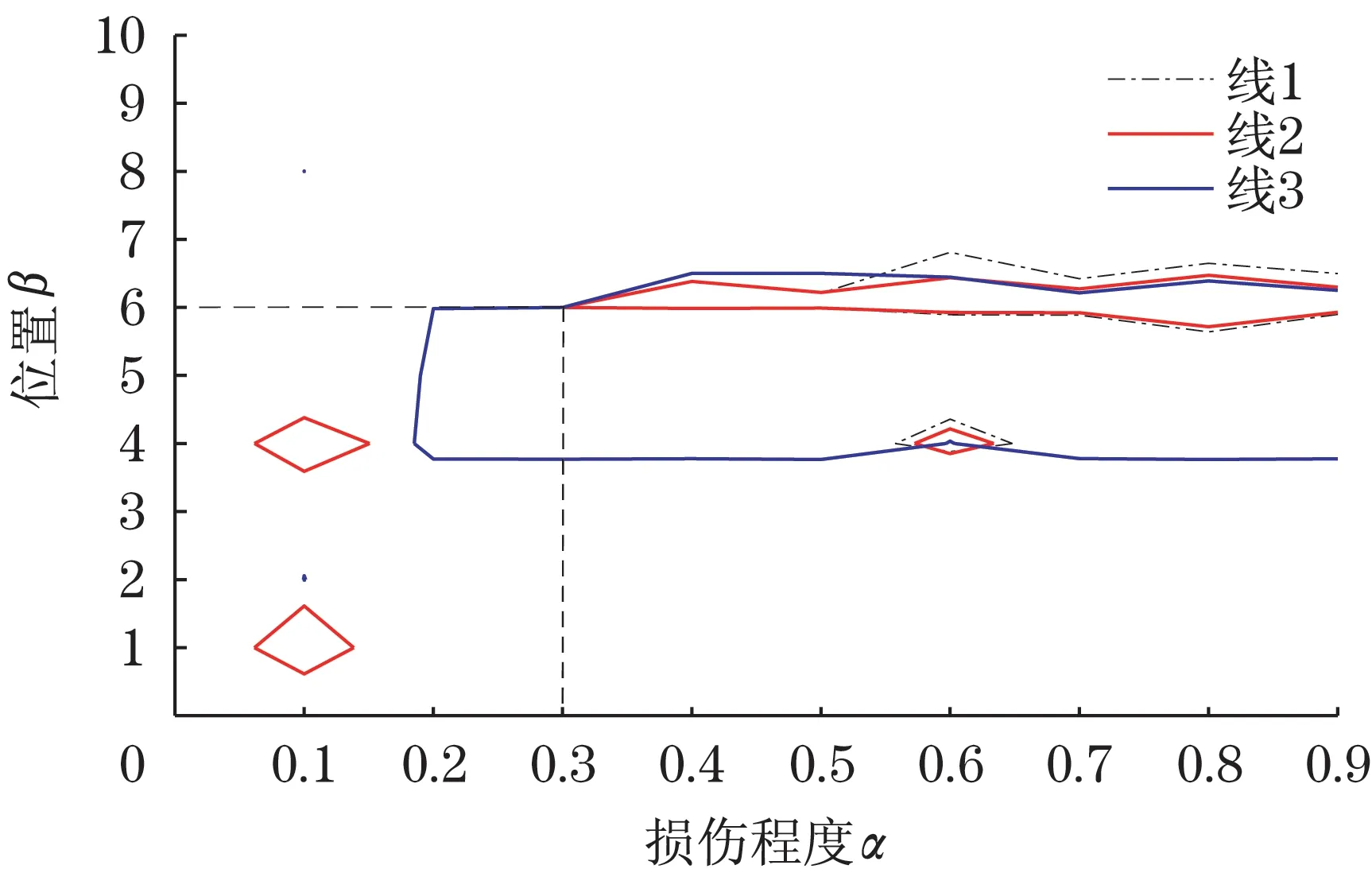
图10 工况5Fig.10 Working condition 5

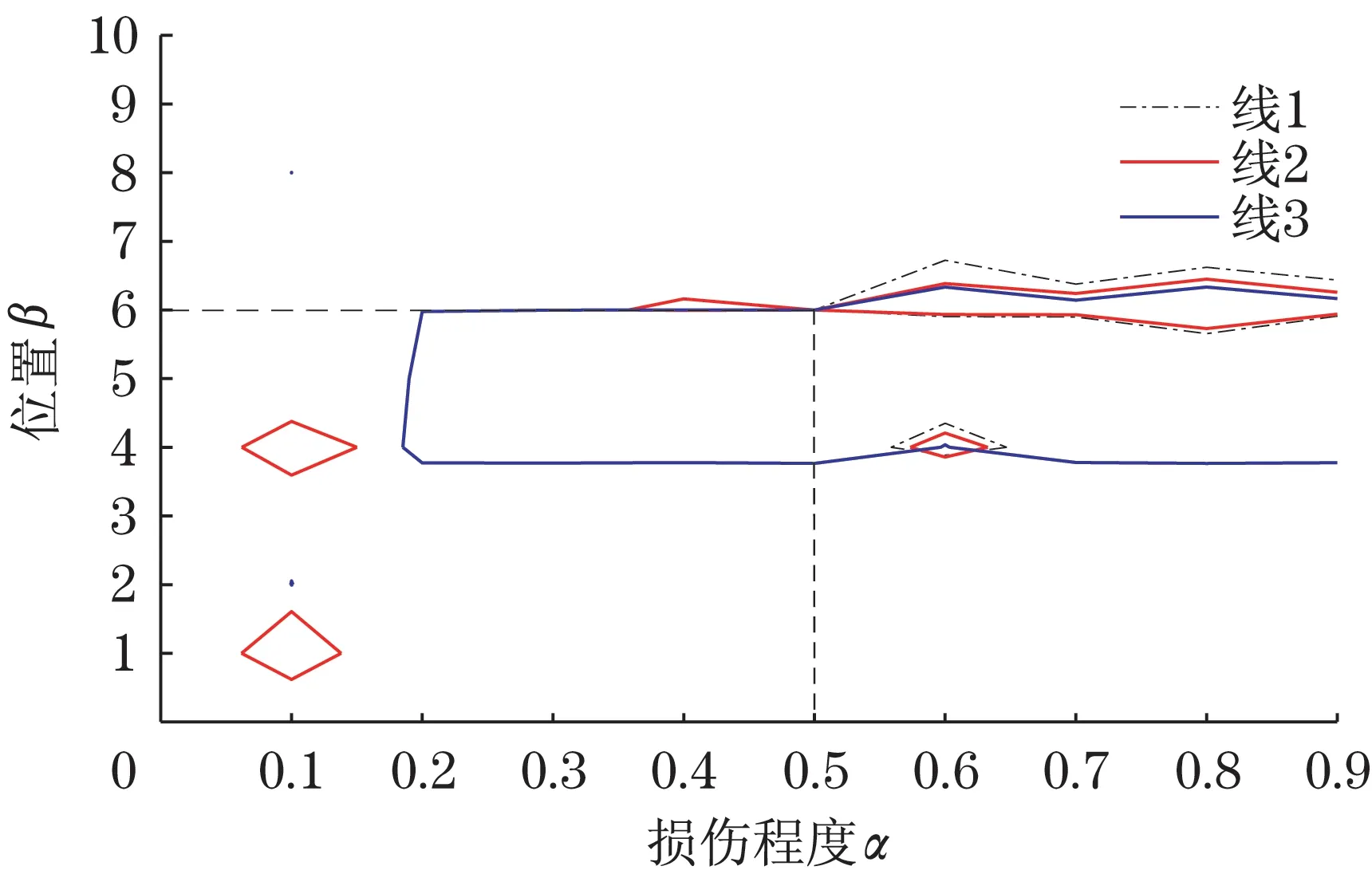
图11 工况6Fig.11 Working condition 6

4 结论

利用ANSYS有限元分析软件对具有疲劳损伤裂纹的桥式起重机主梁进行模态分析，根据起重机不同损伤工况下同阶及非同阶模态频率的不同，通过前三阶模态频率结合等高线相交理论方法，可以直观、定量地得到裂纹存在的位置和裂纹的损伤程度。等高线相交法不用建立庞大的数据库，计算效果较好，且三线等高相交法对输入频率干涉不大，鲁棒性较好，是一种较好的起重机金属结构损伤识别法。