复杂山区铁路客运站自动选址研究
2021-04-29严基团
严基团
(中铁第一勘察设计院集团有限公司 轨道交通工程信息化国家重点实验室,陕西 西安 710043)
0 引言
随着川藏铁路的规划建设,我国铁路选线进入了世界上地形、地质最复杂的地区之一。同时,铁路建设标准不断提升,线路与环境的适应能力大幅降低,桥隧构筑物不可避免地大量增加,空间线位与车站布设的协调问题变得尤为突出。
无备选站址条件下的车站自动选址是线站协同优化的前提和基础。针对复杂山区车站自动选址问题,专家学者进行了大量研究。王齐荣等[1]对车站选址中定性、模糊的评价因素和因素的相对重要性提出量化方法,建立了一种扩充与或图的深度优先搜索算法,并开发了原型系统。Samanta 等[2]依次采用蚁群算法、蚁群与遗传算法相结合对铁路车站的智能选址进行了长期深入研究,提升了优化效果。牛惠民等[3]构造了基于车站选址和地方车流优化组织为核心的NP-Hard 数学模型,提出利用遗传算法求解模型的主要策略,并进行了仿真设计。蒲浩等[4]以综合地理信息模型为基础,基于灰色关联分析理论,计算站址的综合代价,实现了铁路车站的自动寻优。综观国内外针对此问题的研究,现有的方法及其理论均为针对车站选址代价最小化,未考虑站与站之间的区间线路代价。针对以上问题,研究首先建立综合地理信息模型,解决单个车站的选址问题;其次通过2 个车站间的自动选线实现站站连接,将连接2 个车站的区间线路代价作为方案总代价的重要组成部分;最后综合车站的选址代价和区间线路代价,得出满足要求的站址方案群。
1 复杂山区铁路客运站自动选址模型构建与算法
1.1 建立综合地理信息模型
不论是车站选址还是铁路选线,研究范围内的地理信息是基础。将整个方案研究区域划分为(M/d)×(N/d)个正方形的规则网格,其中M,N为研究区域的长和宽,d为用户指定的正方形单元格边长,每一个网格作为地理信息模型的一个单元。把网格内地形、地物、地质、地价等信息作为其属性数据[5],通过网格属性数据即可计算车站或线路占用该网格所代表区域的综合代价。
网格属性数据的设置依据方案比选参考的指标。属性信息分为固定信息、可变信息和禁区信息。固定信息是指不随方案变化的常属性,如网格的地面高程、地物、地质条件、地类。针对方案研究阶段,研究区域内的地形数据可以直接从相关网站上下载。地质信息优先考虑收集研究区域内的既有项目地质资料,若无资料可以参照区域地质图。可变信息是指随着方案变化而变化的信息,如网格的设计高程、工程技术代价(架桥、挖隧)。禁区信息代表方案必须绕避的区域,可能是常量信息,如网格是否位于生态保护区、是否位于永久基本农田区;也可能是变量信息,如桥站的最大桥高。禁区信息能有效地剔除不良方案,提升自动获取方案群的效率,它不作为网格综合代价计算的属性信息。
研究按车站网格和区间线路网格分别设置属性信息来说明网格综合代价的计算方法,其他属性可以依据方案比选时的指标自行增加。
1.1.1 常量属性代价计算
区间线路网格的常量属性包括地质、地物、地类。给定不同地质条件下地基处理代价、不同地物的拆迁代价、不同地类的单位征用代价,通过网格区域所属的地质条件、地类以及所拥有的地物来确定网格的地质代价CL1、地类代价CL2、地物代价CL3。吸引客流量是客运站选址优劣的重要评判标准,故车站网格属性在区间线路的基础上增加客流量吸引力CZ4。CZ4越大代表车站吸引客流的能力越强,故CZ4与客运站到吸引范围内居民区的距离成反比,与居民区的人口数量成正比。假定车站吸引范围内有m个居民区,则车站网格的客流量吸引力计算如公式(1)所示。
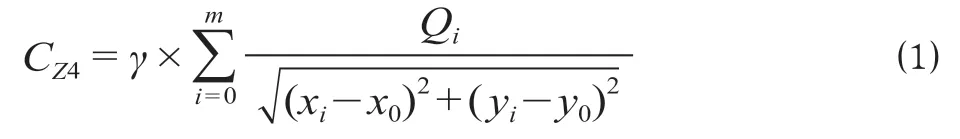
式中:γ为比例常量,用于将客流量吸引力与其他代价转化为同一量级;Qi为第i个居民区的人口总数,万人;(xi,yi)为第i个居民区中心网格的平面坐标;(x0,y0)为车站站心网格的平面坐标。
1.1.2 变量属性代价计算
车站和区间连接线的方案确定后,方案途经网格的设计高程H设即可求出。假定路桥分界填高和路隧分界挖深分别为Ta,Wa。依据网格的设计高程H设和地面高程H地计算网格的土石方工程代价V1和工程技术代价V2。
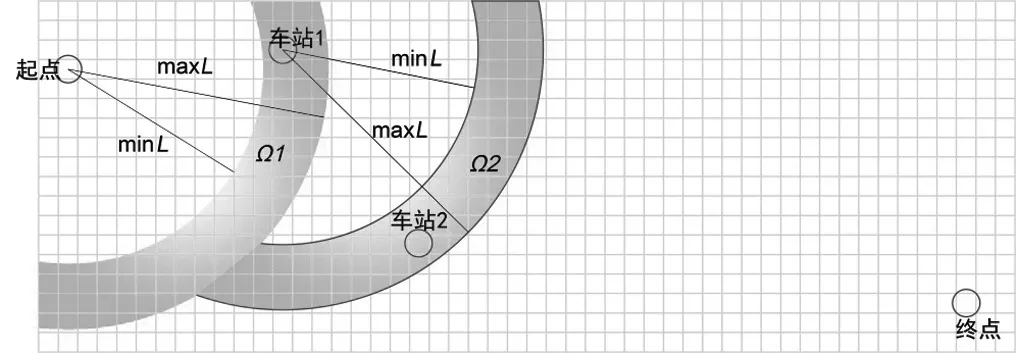
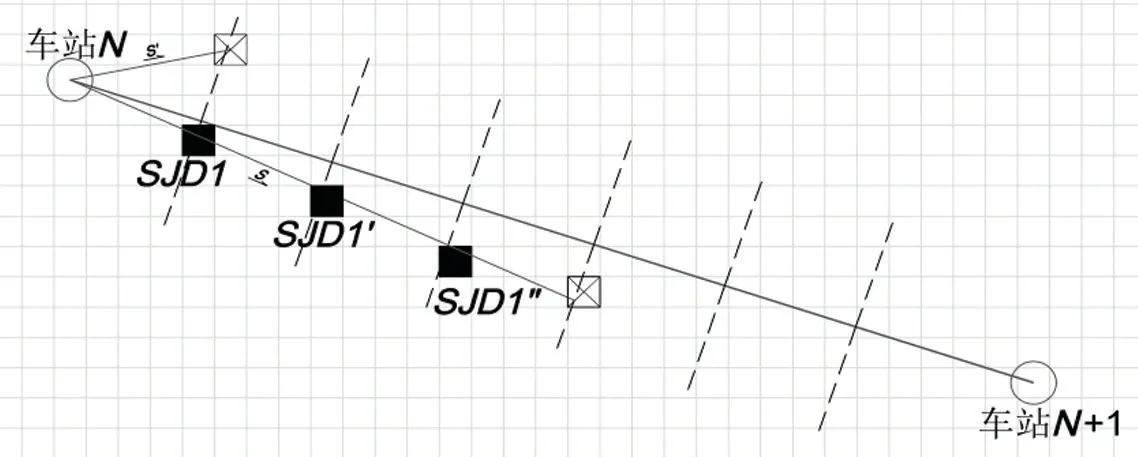
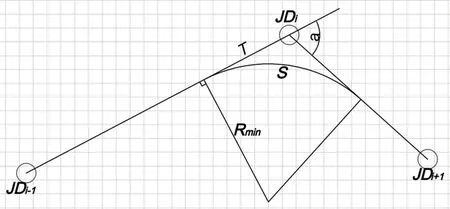
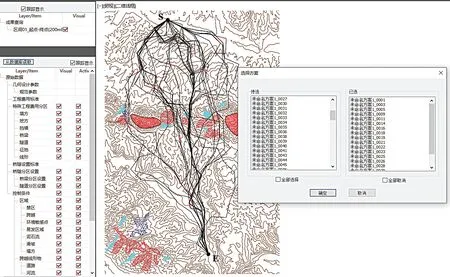
当H设-H地> 0 且H设-H地 式中:γ1为填方填料和施工综合代价,万元/m3;d为正方形网格的边长,km。 当H设-H地>Ta,网格需要设桥,V1为0,V2计算如公式(3)所示。 式中:γ2为不同桥高的桥梁工程代价,万元/m。 同理挖方类似。由此通过变量属性得到网格在不同方案下的土石方代价和工程技术代价。 综合网格常量属性和变量属性,分别计算网格对应的各属性代价,并给各属性代价赋予相应的权重,即可得到网格的综合代价。 1.2.1 站心备选区域 根据经调及行车资料确定最大站间距(maxL)、最小站间距(minL)。以已知车站站心所在位置为圆心,分别以maxL和minL做圆,2 个圆围成的圆环区域即为相邻车站的站心备选区域。站心备选区域如图1 所示。已知起点站和终点站的站心位置,各车站备选区域求解步骤如下。 (1)以起点站为圆心,以maxL,minL画圆,图1 所示圆环区域Ω1 即为车站1 的站心备选区域。 (2)以Ω1 内的站心可行解所在网格为圆心,继续以maxL,minL画圆,得到圆环区域Ω2 即为车站2 的站心备选区域。依次迭代,得到后续车站的站心备选区域。 (3)当任意车站的后续车站站心备选范围包含终点网格,则所有车站站心备选区域求解结束。 1.2.2 确定站心可行解 站心备选区域内网格数量众多,若不加筛选直接进行后续计算,会导致计算量异常庞大,从而导致自动生成方案的效率大幅下降,因此要在备选区域内剔除不满足设站条件的网格。研究采用禁区信息、展线系数、站心高程、线路行进方向耦合度4 个控制因素来筛选备选区域的站心可行解。 (1)禁区信息。若网格的禁区信息为生态保护区或者永久基本农田区,则站心不可位于此网格。 (2)展线系数。从起点开始,依次连接后一车站,直至需要确定站心位置的第i个车站,然后连接第i个车站站心和终点。若连接线的长度与起、终点航空距离的比值超过了最大展线系数,如公式(4)所示,则该单元格不能作为站心的可行解。 图1 站心备选区域Fig.1 Alternative area of the station center 式中:(Xi,Yi)为站心i在空间网格下的平面坐标;(Xt,Yt)为终点站在空间网格下的平面坐标;L为线路起终点在空间网格下的航空距离,km;Zmax为最大展线系数。 (3)站心高程。由于坡度和区间线路尚未确定,站心的设计高程无法计算。当区间线路长度都为最大站间距maxL、曲线连接线路坡度都为最大坡度imax,求得的第n个车站的站心高程都不能满足公式(5),即表示在规定的坡度范围内,站心高程高于给定的最大桥高hmax1或低于允许最大挖方hmax2需设置隧道,故该网格地面高程不满足设站条件。 式中:H0为起点车站站心网格的实际高程,m;H地为第n个车站站心网格的地面高程,m。 (4)线路行进方向耦合度。客运站的设置应该是沿着线路走向,以便乘客尽可能快地到达目的地,若相邻车站连线方向与起终点连线方向相反,如公式(6)所示,则该站心网格不满足设站条件。 式中:(Xi,Yi)为车站i站心网格的坐标;(X0,Y0)为起点站站心网格的坐标;(Xt,Yt)为终点站站心网格的平面坐标。 1.2.3 站坪方向的确定 将车站站坪区域视作长为L/d个单元格、宽为B/d个单元格的矩形区域。其中L,B分别为站坪区域的长和宽,d为用户指定的正方形单元格边长。以任意站心可行解所在的单元格为矩形中心,以固定角度绕矩形中心旋转一周得到若干备选方向。任意方向的站坪区域若包含单元格属性为禁区信息,则该站坪方向不满足强制性约束条件,该站坪方向方案剔除。若站心无满足条件的场坪方案,则该站心网格从站心可行解中剔除。 由于站心位置和站坪方向已经确定,相邻2 个车站的站心看做已知的起、终点,站坪方向看做车站的接线方向,故站—站间自动选线问题可以看做是已知起终点和接线方向的智能选线。针对该问题,文献[6]提供了基于公路线形优化(Highway Aligment Optimization,HAO)模型[7]的改进遗传算法。研究在HAO 模型的基础上采用一种简化算法。 1.3.1 平面设计 线路的平面几何信息可以通过平面交点的经纬坐标(N,E)、曲线半径R、缓和曲线长度Lo描述。实际设计中缓和曲线长度根据曲线半径自动选配,因此其长度直接选取对应曲线半径的推荐值。 基于HAO 模型,在相邻车站连线的法向上按一定间距生成一系列的截面。线路交点就位于这些截面上。 (1)交点的可行解。由于车站N的站坪方向已经确定,以车站N站心为原点分别沿站坪方向S和S′做射线与各截面相交,直至交点所在单元格属性包含禁止属性为止。交点可行解集示意图如图2 所示。S方向交点集ΩS={SJD1,SJD1′,SJD1″};S′方向与第1 个截面的交点就在包含禁止属性的单元格里,S′方向的交点集ΩS′=φ,这就表示该站心位置按照此站坪方向接线条件极为不利,该站心位置的此站坪方向方案要剔除。当站坪方向交点集不为空,交点集内的每一个元素都可以作为交点备选。 确定了交点JD1后,可以参照上述方法,将JD1作为起点以任意等角度差做射线与截面求交直至交点所在单元格属性包含禁止属性为止求得JD2备选区域,依次往后。 (2)规范合规性检测。当2 个车站间m个交点的备选区域的单元格个数分别为n1,n2,…,nm个时,则站—站间的区间线路方案共有n1×n2×…×nm个。显然,这样会产生巨大的计算量。铁路线路规范对最小曲线半径、最小夹直线长有强制性规定,可以通过交点的合规性直接剔除不合理的方案。 依据上述方法求得的交点位置示意图如图3 所示。交点JDi-1,JDi,JDi+13 个交点形成的转角为a,则3 点间应满足公式(7)。 图2 交点可行解集示意图Fig.2 Diagram of feasible solutions for intersection points 图3 交点位置示意图Fig.3 Diagram of the intersections position 式中:(xi,yi)为在空间网格下的坐标;Rmin为最小曲线半径,m;Lmin为最小夹直线长度,m。 如交点不满足合规性,不做后续计算,直接剔除该方案。 1.3.2 纵断面设计 文献[8]基于HAO 方法建立了公路线路的纵断面优化模型,但该方法中变坡点的个数及位置与平面交点是一致的。在实际的铁路选线设计中,变坡点和平面交点个数往往不一样,且为了尽量避免平、竖曲线重叠,位置也不同。纵断面设计首先需要确定变坡点的个数及位置,然后再通过建立目标函数求解相邻变坡点的最优坡度。 (1)变坡点个数及位置的确定。变坡点的设置与地面线的起伏情况是密切相关的,而原始地面线是不规则的锯齿形折线,因此需要对地面线拟合成一条光滑的曲线后根据曲线起伏突变来确定变坡点的个数和位置。地面线拟合的方法很多,文献[9]采用屋架函数建立分段的地面模型,随机选取不同的平顺半径和平顺次数生成变坡点的个数N,依据最小坡段长的要求,变坡点个数N必须满足公式(8),否则重新选择平顺半径和平顺次数重新生成变坡点个数。 式中:L为已求得的区间线路长度,m;LSmin为最小坡段长度,m。 变坡点个数确定后,按照最小坡长LSmin的要求,第i个变坡点的里程范围Si需满足公式(9)。 式中:Ss为区间线路起点里程;Se为区间线路终点里程。 为了避免平、竖曲线重叠,变坡点里程的取值范围应剔除平曲线所在区域。在筛选后的区域内随机取值即可得到变坡点的里程。 (2)求解坡段的最优坡度。综合考虑土石方工程代价、桥隧工程代价和填挖平衡,三者的权重分别为α,β,γ,则纵断面坡度S目标函数如公式(10)所示。 设Pi(ki,hi)和Pi+1(ki+1,hi+1)为同一坡段上相邻的前后2 个变坡点;ki,hi分别为Pi的里程和高程。在(ki,ki+1)区间内任取j个桩号,第m个桩号处的里程和地面高程分别为km,hm,路桥和路隧分界填挖分别为hb,ht。 当hm 当S×(km-ki) +hi>hm+hb,假定不同桥高对应每米高差设桥代价为β1,则增加后的桥梁工程代价如公式(12)所示。 当hm-ht 当S×(km-ki) +hi 当F(S)的值最小时,对应的坡度S为最优坡度。该目标函数直接求解参数S比较复杂,可以通过计算机迭代计算。限制坡度为Smax,不考虑坡度折减的影响,在(-Smax,Smax)以初值为-Smax开始按照特定步长迭代计算,F(S)取得最小值时对应的S为该坡段的最优坡度。 (3)合理性检测。从区间线路起点开始依次组合变坡点的位置和坡度信息,即可完成区间线路的初步纵断面设计。 分坡段求解最优坡度时,没有考虑相邻坡度的影响。考虑最大相邻坡度代数差ΔSmax的限制,最优坡度Si为公式(16)所示。 最优坡度求解是基于随机的离散桩号构建的目标函数,对隧道工程代价没有考虑隧道长度的影响。假定允许最大隧道长度为LT,在求出最优坡度后,依据已述方法判断网格是否需要设置隧道,得到需要设置隧道的最大连续网格数N,当N不满足公式(17)时,表示隧道长度超限,方案舍去。 式中:d为网格边长,km。 车站评价指标集为IZ= {IZj,j= 1,2,…},指标权重为WZ= {WZj,j= 1,2,…};区间线路评价指标集为IX= {IXj,j= 1,2,…},指标权重为WX= {WXj,j= 1,2,…}。依据上述网格代价计算方法,遍历方案的所有车站网格和途经区间线路网格,车站M网格对应指标集IZ的代价为CZ= {CZMj,j= 1,2,…},区间线路N网格对应指标集IX的代价CX= {CXNj,j= 1,2,…}。自动生成的方案示意图如图4 所示。设方案共设K个车站,计算该方案综合代价为公式(18)所示。 将各方案的综合代价排序,即可实现铁路站址的综合优选。 选取西成铁路(西宁—成都)某区段案例验证本方法的有效性。研究区域地形图如图5 所示。该区域面积为4 620 km2(55 km×84 km),线路起点高程2 150 m,终点高程2 070 m。起终点间高山密布,平均高程约为4 000 m,属于复杂山区铁路选线案例。 图4 自动生成的方案示意图Fig.4 Diagram of automatic generated scheme 图5 研究区域地形图Fig.5 Topography map of the studied areas 该铁路需满足的约束条件如表1 所示。 表1 需满足的约束条件Tab.1 Required constraints 该算例采用的费用标准如表2 所示。 2.2.1 设置搜索参数 设置参数包含最小站间距、最大站间距、站坪长度、站坪宽度及展线系数等,本算例搜索参数设置如表3 所示。 2.2.2 方案搜索及筛选排序 从线路起点开始,以终点作为目标点,根据各单元格所记录的信息生成包含车站的方案集合。搜索过程耗时约为7.5 h,生成的方案集合如图6所示,共64 个。经过综合代价排序,筛选出最优方案,机选的最优方案与人工方案对比如图7 所示。 表2 费用标准Tab.2 Cost standard 表3 搜索参数设置Tab.3 Search parameter settings 图6 生成的方案集合Fig.6 Automatic generating schemes 由图7 可知,机选方案和人工方案都绕避了禁区。机选方案生成的站址均位于直线、平坡地段,并且未与桥、隧重叠;人工方案在线路起点附近站址有部分位于曲线段并且进入隧道范围内。因此,机选方案能更好地满足约束条件。 依据设定的工程代价指标,机选最优方案与人工方案数据对比如表4 所示。 由表4 可见,人工方案虽然桥梁工程较少,但其隧道与土石方工程均显著增加,导致工程费用比机选方案增加约8.96 亿元,最终机选方案相比人工方案在给定的费用标准下,工程费综合代价降低了约18%。 针对无备选站址条件下的车站自动选址问题,考虑车站选址和相邻车站的区间线路的综合代价,首先,将研究区域划分为带地理信息的正方形网格,以便通过网格的属性信息求解网格的各指标代价;其次,通过限制条件在站心和站坪方向的备选区域中筛选出满足要求的站心位置和站坪方向;再次,基于HAO 模型进行区间线路设计,得到满足平、纵约束的区间线路;最后,遍历车站范围内网格和区间线路途经网格,计算综合代价进行排序,实现方案的优选。 研究主要特点:①将车站选址和区间线路设计紧密联系起来,以车站选址和区间线路的综合代价作为方案优劣的评价因素,更加体现线站一体化的设计理念;②基于约束条件,后续设计成果会对前设计成果进行约束检测,持续剔除劣解。基于本方法,可以高效地实施站址评选,提供较优的方案群供设计人员参考。 图7 机选的最优方案与人工方案对比Fig.7 Comparison of automatic scheme and manual selection scheme 表4 机选最优方案与人工方案数据对比Tab.4 Comparison of automatic scheme and manual selection scheme data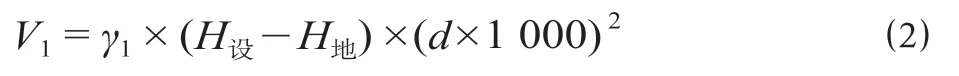

1.2 单个车站选址
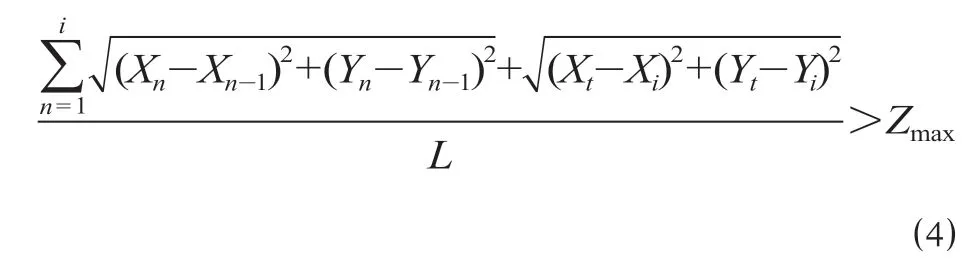
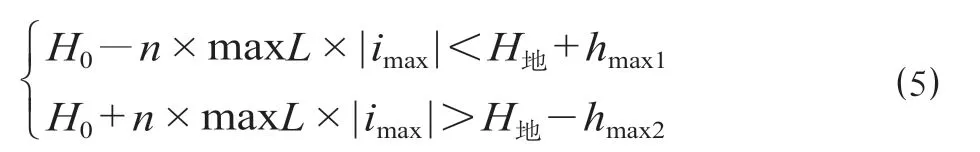
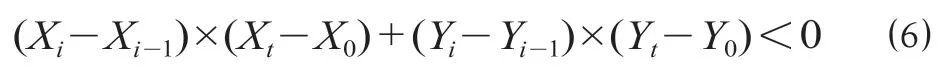
1.3 站—站间自动选线
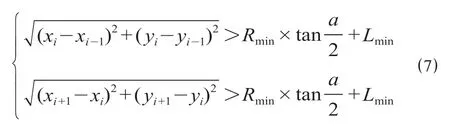



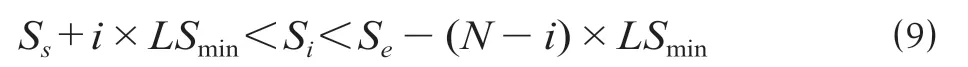
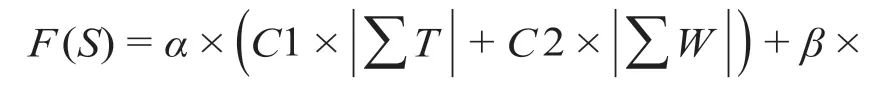

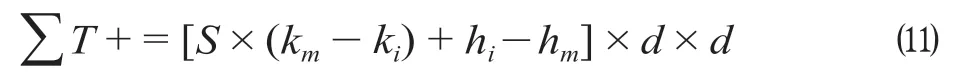
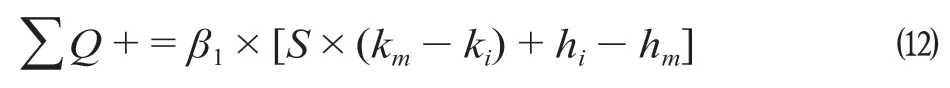
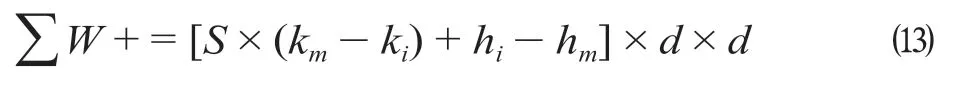
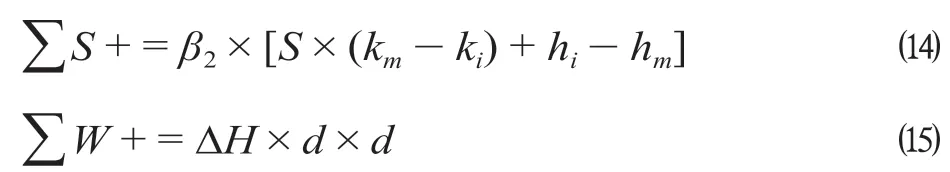
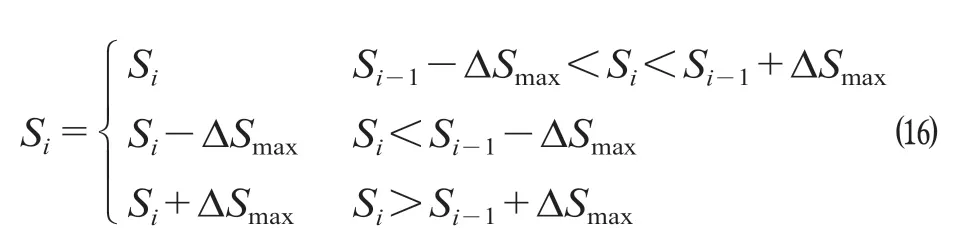

1.4 计算综合代价
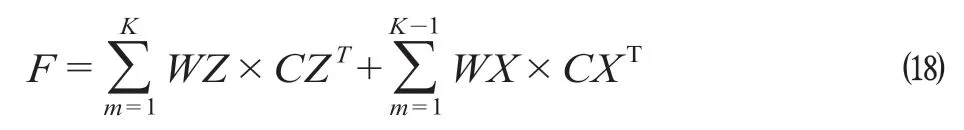
2 算例分析


2.1 主要约束及费用标准

2.2 优化过程及结果分析


3 结论