高速铁路柔性时刻表编制研究
2021-04-29李嘉义李得伟
李嘉义,李得伟
(北京交通大学 交通运输学院,北京 100044)
需求响应型交通(Demand Response Transit,DRT)是一种由乘客通过手机、电话或PC 终端实时预订行程的非固定线路的公共交通人员运送交通模式,网约车、定制公交作为需求响应型交通的代表,目前已经成为运输组织领域的研究热点。需求响应型运输模式能够缓解运输领域供需不平衡的问题,实现精准运输服务,在高速铁路领域同样有较大应用潜力。与传统的时刻表不同,需求响应型运输模式下的运行图中部分运行线是柔性的。旅客通过预约系统提交出行需求后,预约系统快速做出响应,生成匹配旅客预约出行时间的实际运行线,解决供需信息不对称问题,实现资源的有效配置。
国内外针对这一问题的研究尚处于起步阶段,主要集中在定制公交领域,刘冬梅[1]设计了西安市定制公交的运行方案,并对车辆组织管理和车辆配置策略等进行了研究。徐康明等[2]分析了定制公交系统的服务要素、优势和开行的主要条件。由于客流组织形式、车辆运营管理方式的不同,定制公交的相关理论无法直接应用于高速铁路[3-8]。
针对这一问题,根据预约旅客占全部旅客的比例,提出高速铁路完全柔性和部分柔性2 种编制模式。完全柔性是指全部出行旅客都需要通过预约系统提出预约需求,列车运行图上所有运行线均由旅客在预约系统中提供的预约出行需求信息确定。考虑到在运输组织由规划型向需求响应型转变的过程中,可能会经过刚性、柔性共存的过渡期,或者一些线路上有部分较为稳定的出行客流需求,所以提出部分柔性模式,即只有部分旅客提供预约需求。因此,运行图的编制问题也转变为在原有图定运行线的基础上加开柔性运行线。
1 模型与算法
1.1 问题描述
高速铁路柔性时刻表编制问题主要是为每一条弹性旅客出行预约需求提供响应,并决策是否开行及如何开行需求响应型列车,其核心是构建科学的弹性预约客运需求分配及柔性时刻表优化模型。主要难点在于旅客提交的预约出行需求具有不同出发时间、出发地点、到达地点,以及预约出行旅客对应的可行分配方案数量巨大,造成数据规模庞大,难以求解。由于预约出行服务应具有更高的服务质量,因此考虑了平均偏差时间,即实际出行时间与预约系统提交的计划出行时间的差值,同时,列车开行具有一定的成本,从运营商角度应保证列车开行收益。为解决上述问题,设计了双层规划模型,上层规划模型以收益最大化为目标,下层规划模型以旅客平均偏差时间最小化为目标,根据旅客的预约出行需求,基于一定优先级为每个需求分配服务资源;在整个过程中,设计模拟退火求解算法,最终可以得到预约需求分配方案及柔性时刻表。
柔性时刻表编制模型框架如图1 所示。模型输入包括3 部分:列车开行参数包括车站研究时间范围、列车定员、停站方案、各区段距离及运行时间、各区段票价、列车开行成本、旅客时间成本;预约需求数据包括始发站、终到站、计划出行时间;算法参数包括初始温度、结束温度、温度衰减参数、链长。模型输出包括时刻表和预约需求分配情况,评价时刻的指标为实际出行时间与预约系统提交的计划出行时间的差值、预约需求满足比例以及预期收益。
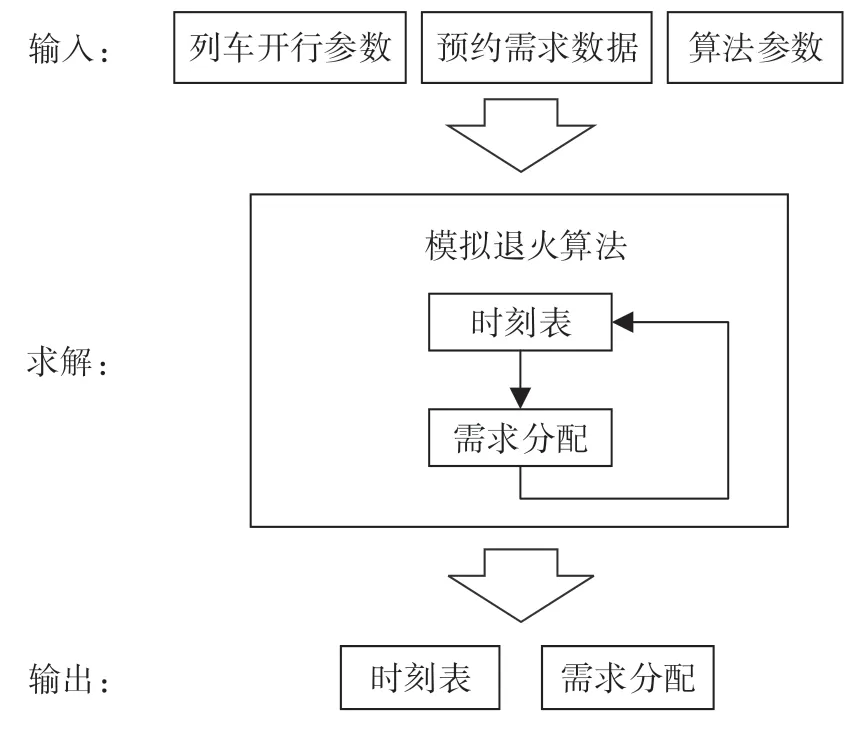
图1 柔性时刻表编制模型框架Fig.1 Model framework of flexible timetable design
1.2 模型定义
为方便建模,提出以下假设:①列车区间运行时分、最小追踪间隔时间、停站方案及停站时间均为固定值。②动车组数量充足,能够满足全部旅客的出行需求。③所有柔性运行线均为同一等级列车,同等级列车间不发生越行。④在部分柔性时刻表的编制过程中,图定线不可做任何更改。
模型定义若干符号,符号及定义如表1 所示。
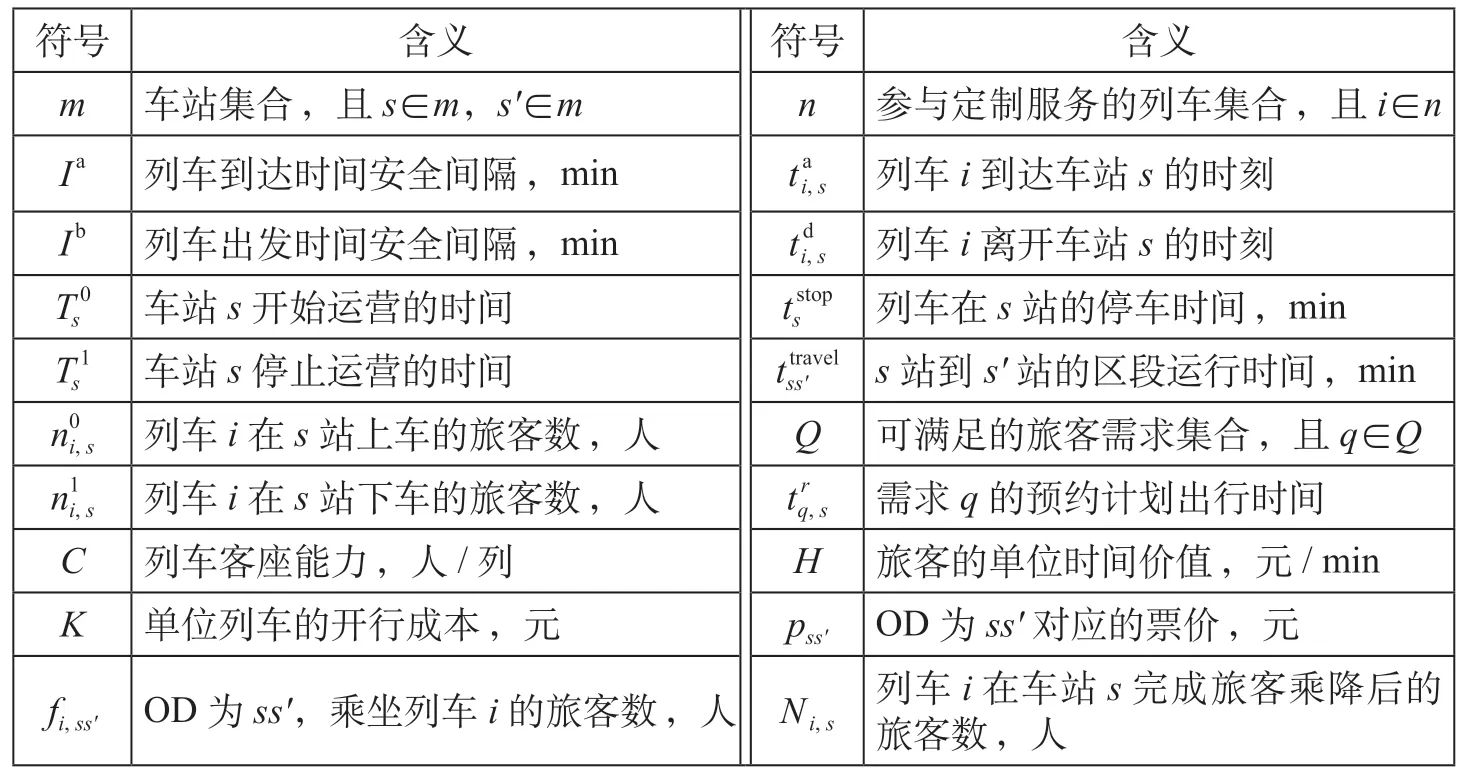
表1 符号及定义Tab.1 Symbols and definitions
1.3 模型编制
1.3.1 高速铁路完全柔性时刻表编制模型
高速铁路完全柔性时刻表编制模型的编制思路如下。
(1)根据始发站的预约需求数,按照上座率为100%确定初始参与服务的定制列车数,随机确定初始的列车始发时刻,根据区段运行时间和停站时间产生初始时刻表,并按照平均偏差时间最小为原则将预约需求分配到列车上,计算开行收益。不断修改列车始发时刻,直至找到当前定制列车数下的收益最高时刻表。
(2)增开1 列定制列车,并按照第1 步的方法求出对应列车数下的最优解。
(3)重复第2 步操作,直至找出全局最优时刻表及其对应的预约需求分配方案。
高速铁路完全柔性时刻表编制模型包括2 层,上层为时刻表优化模型,下层为客流分配模型。上层规划模型的重点是确定参与定制服务的列车数,并在满足列车安全运行间隔的前提下确定各列车在规划范围内的到达、离开车站的时间。其目标是最大化当前时刻表的收益,如公式(1)所示。

模型约束条件为

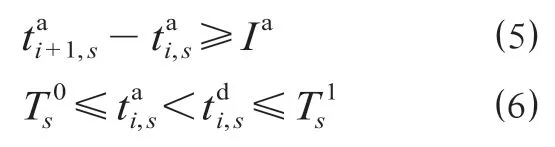
式中:U为开行收益,元;q为得到满足的旅客预约出行需求;pss′表示区段s-s′的票价,元;n为定制列车数列;K为单位列车开行成本,元;H为旅客单位时间价值,元/min;F为满足需求旅客的平均偏差时间,min。
公式(1)中开行收益由3部分组成,第1 部分表示票务收益,第2 部分表示列车开行成本,第3 部分表示旅客的偏差时间成本。公式(2)为列车区间运行时间约束;公式(3)为列车停站时间约束;公式(4)和公式(5)为列车安全间隔约束;公式(6)为列车开行时段约束。
下层规划模型将预约需求分配到时刻表不同的运行线上,目标是使满足预约需求的旅客平均偏差时间最小,如公式(7)所示。

上下2 层模型之间的关联关系如下:上层模型的旅客偏差时间成本由下层规划模型的平均偏差时间×旅客单位时间价值得到;下层规划模型根据上层规划模型制定出的时刻表进行客流分配。
公式(8)表示列车满足的各OD 需求数等于可满足需求总数;公式(9)表示列车满足的各OD 需求数非负;公式(10)表示旅客是否有机会乘坐第i列车与列车出发时刻的关系;公式(11)、公式(12)为列车客座能力约束。
1.3.2 高速铁路部分柔性时刻表编制模型
高速铁路部分柔性时刻表编制模型的编制思路如下。
(1)利用原有图定列车的空余客座能力解决新增的预约需求,将剩余未满足的预约需求作为输入条件,采用与完全柔性相同的模型进行求解。
(2)在利用原有图定列车解决预约需求时,给定旅客获得服务的平均偏差时间为ΔT,认为偏差时间在ΔT时间内,旅客均可接受,即不考虑平均偏差时间的影响。如旅客计划出行时间为t,则在[t- ΔT,t+ ΔT]内到达该站的列车,旅客均可接受乘坐该车以解决出行需求。按照最大化客票收益的原则,选择可以满足预约需求的旅客,如公式(13)所示。

式中:P表示客票收益,元;q为得到满足的旅客预约出行需求;pss′表示区段s-s′的票价,元。
(3)在利用加开的柔性运行线解决剩余预约需求时,不能对图定列车进行调整,因此列车组成的时间间隔应属于原运行图的空余能力区间T′。

1.4 求解算法
因开行定制列车的数目是未知的,且每一列车的改变都会影响到下层模型需求分配的求解,影响整个时刻表的优劣,因此设计了基于模拟退火算法的求解方法。求解过程流程图如图2 所示。
2 案例分析
为了验证模型的有效性,综合考虑我国高速铁路线路,并结合高速铁路柔性时刻表的适用条件,以厦深高速铁路(厦门北—深圳北)为例进行案例分析。厦深高速铁路为双线铁路,案例只研究从厦门北至深圳北方向,并保留客流较为集中的10 个车站,构建一个由10 个车站和9 个区段组成的测试线路。厦深高速铁路线路示意图如图3 所示。

图2 求解过程流程图Fig.2 Flow chart of solving process
2.1 完全柔性时刻表编制案例
完全柔性时刻表编制将按照以下4 个步骤展开。
步骤1:参数设置。设定在厦门北站可选择的出发时间范围为7 : 00—20 : 00,依据区段运行时间以及停站时间,计算出途经各站可选择的出行时间范围。本次试验不考虑席别差异以及旅客对于席别的特殊需求,假设所有旅客均选择二等座,票价参考当前实际票价,同时实验不考虑列车编组问题,所有列车定员800 人/列。根据周文梁等[9]的研究,列车的开行成本由2 部分组成,列车单位时间运营成本及开行固定组织成本,开行固定组织成本为4 000 元/列,列车单位时间运营成本为9 000 元/h,厦门北开至深圳北历时约3.75 h,单位列车开行成本为3.75×9 000 + 4 000 = 37 750 元。旅客单位时间价值取37.8 元/h[9]。区段运行时间和停站时间如表2 所示。算法初始温度T0= 999,结束时温度Tmin为0.01,链长为100,温度衰减参数h= 0.97。

图3 厦深高速铁路线路示意图Fig.3 Illustration of Xiamen-Shenzhen high speed railway

表2 区段运行时间和停站时间Tab.2 Section operation time and stop time
步骤2:输入预约需求数据。以2020 年12月9 日厦深高速铁路票务数据为基础,假设由厦门北开行至深圳北方向当日的预约客运需求共21 761人,分布于线路所含10 个车站,需求OD 分布表如表3 所示。设定高峰出行时段为8 : 00—10 : 00和17 : 00—19 : 00,并设定选择高峰时段出行的旅客概率是平峰出行的2 倍,将旅客的计划出行时间平均分布在各站开行时段内。
步骤3:生成初始解。根据预约需求数据,假设上座率为100%,初步确定参与定制服务的列车数为n= 5。计算此时目标函数U= 141 954。
步骤4:迭代求解。在原有参与定制服务的列车数基础上,加开1 列列车,即参与定制服务的列车数n变为n+ 1,按照上述计算方法,根据时刻表和其对应的客流分配情况计算出最优收益U2。如果n+ 1 列车获得的收益大于n列时获得的收益,即U2>U1,则加开列车,n替换为n+ 1。重复上述操作,直至n不再发生改变。列车开行利润变化如图4 所示。
求得的结果为:参与定制服务的列车数为19列时达到最优,取得收益最高。时刻表的具体指标信息如表4 所示。列车具体信息如表5 所示。
当参与服务的列车数为19 列时,满足了20 211名旅客的预约需求,需求满足的比例为92.9%,具有较高的需求满足比例,平均偏差时间为35.47 min,单位列车客票收益为85 214.53 元,单位列车取得的利润为47 464.53 元,共取得利润901 826 元,具有较好的收益。

表3 需求OD 分布表 人Tab.3 Demand distribution table
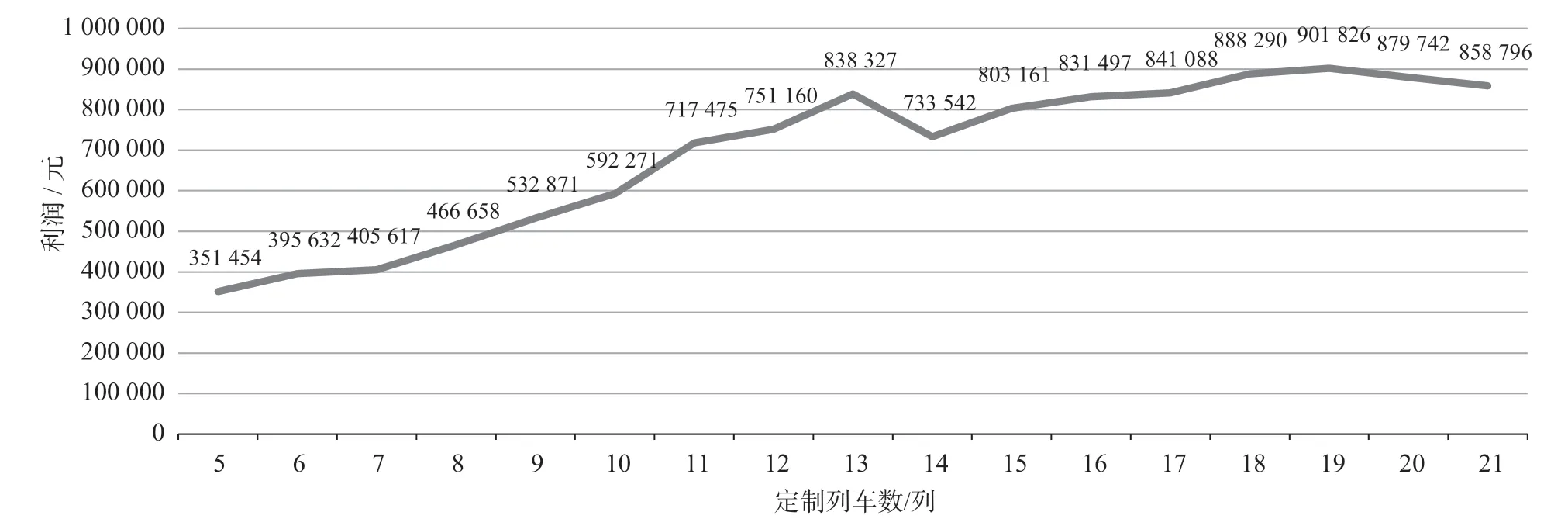
图 4 列车开行利润变化图Fig.4 Profit change of train operation
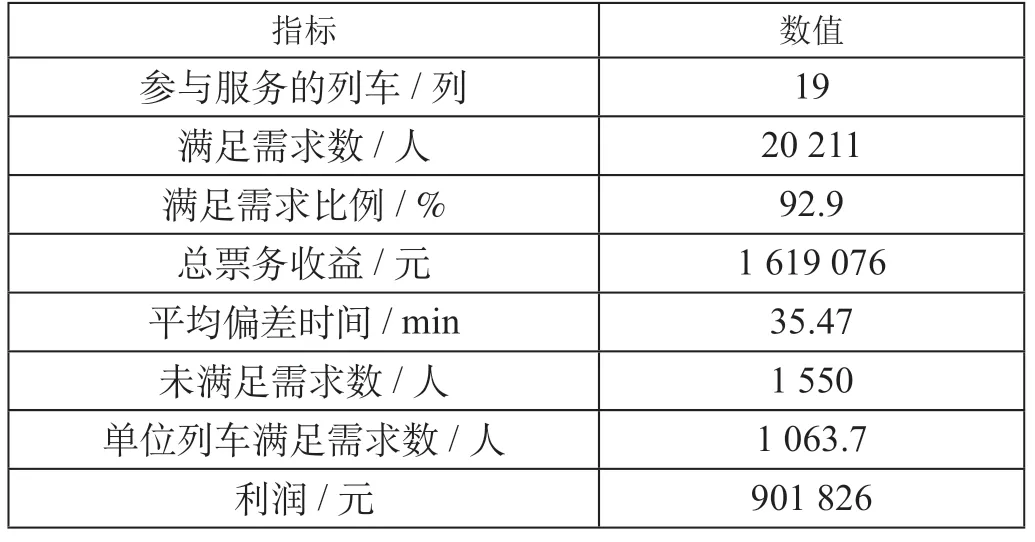
表4 时刻表的具体指标信息Tab.4 Index information of timetable

表5 列车具体信息 人Tab.5 Train information
2.2 部分柔性时刻表编制案例
测试线路仍然沿用厦门北—深圳北线路,相关参数不变,将由完全柔性模型求解而得的时刻表作为初始时刻表,且图定列车不允许做出调整。
步骤1:输入客流数据。假设新增预约需求为2 000 人,客流集中在厦门北、潮汕、普宁3 站,需求分布表如表6 所示。计划出行时间平均分布在17 : 00—18 : 00 间。
步骤 2:首先利用初始图定列车的空余客座能力来满足预约的客流需求。参考上例求得平均偏差时间,取T =30 min,选用分布在[16 : 30—18 : 30]开行的2 列车的空余座位率先解决预约需求,可以解决预约需求数为422 人。
步骤 3:将未满足的旅客预约需求1 578 人作为输入条件,将2.1 节求得的时刻表作为图定运行图,在图定运行线的基础上加开柔性运行线。
求解结果为加开2 列定制列车,其始发时刻分别为18 : 25 与19 : 00,对当前运行图上原有的运行线并未造成影响。新增列车具体指标信息如表7 所示。新增列车具体信息如表8 所示。
对于当前预约客流的处理方法是加开2 列途径厦门北—潮汕—普宁—深圳北站的列车,新开定制列车满足了1 562 位旅客的出行需求,原有图定列车的空余客座能满足422 位旅客的出行需求,共获得利润133 838 元。
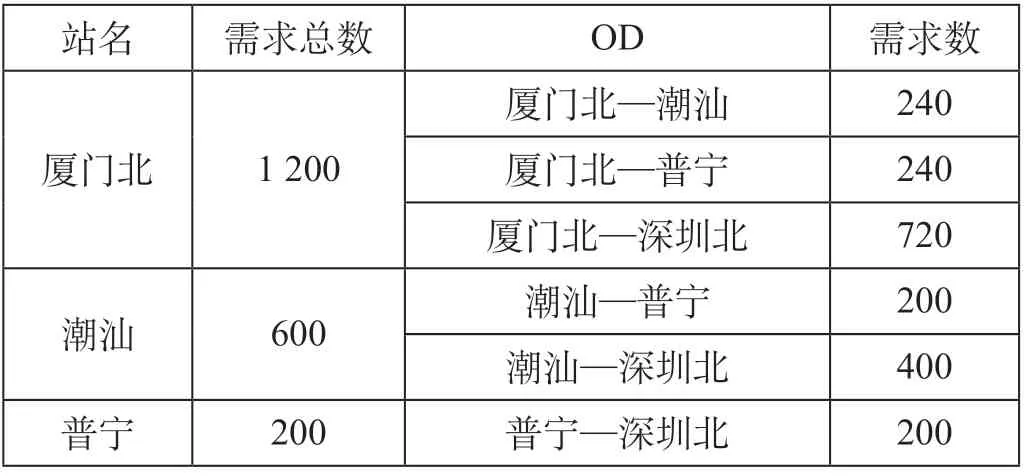
表6 需求分布表 人Tab.6 Demand distribution table

表7 新增列车具体指标信息Tab.7 Index information of additional train

表8 新增列车具体信息 人Tab.8 Additional train information
3 结束语
通过对高速铁路柔性时刻表编制问题的研究,可以更好地掌握旅客的实际出行需求,使列车开行时间与旅客需求匹配,缩短旅客预约时间与实际出行时间的偏差,从而提高服务质量,同时可以优化资源配置,提高列车运营收益。算例结果表明,所设计的模型及算法可行,编制的柔性列车时刻表对于未来需求响应型交通在高速铁路上的应用可以提供有效的参考。然而该模型方法与实际应用还有较大差距,下一步将优化预约机制与运输组织的协调配合、列车交路和停站方案、预约需求分配方式,同时考虑与列车乘务计划、车底周转计划的协调配合,提高柔性时刻表的可操作性。
