高速铁路可变编组列车开行计划优化
2021-04-29卢特尔陈军华陈昂扬
卢特尔,陈军华,陈昂扬,郑 汉
(北京交通大学 交通运输学院,北京 100044)
0 引言
自20 世纪90 年代以来,经过几十年的发展,我国针对不同的区域环境和线路条件,研发了应用于高寒地区、沙漠地区、长大干线、城际线路等不同速度等级、不同运用条件的高速铁路动车组,已经基本形成了自主创新的高速动车组体系结构[1]。高速铁路动车组有很多不同的型号,但是大多为8辆、16 辆或17 辆车厢固定编组,且在运营过程中编组不可改变,导致动车组的载运能力无法很好地适应需求的波动。此外,动车组检修、热备等环节均需要整列同时进行,动车组运用缺乏灵活性,运用效率不高。国外铁路可变编组列车的发展起步较早,应用范围更广,如德国研发的ICE4 于2017年投入运营,可实现5 ~ 14 辆灵活编组[2]。荷兰采用3 辆或4 辆客车形成列车单元,以实现3 ~ 15 辆编组。我国研发的CRH3X 型可变编组动车组样车可以实现多种车型的灵活拆解、组合[3]。2018 年,中车唐山机车车辆有限公司首次发布最高运行速度500 km/h 的可变编组动车组概念车,同时展出运行速度350 km/h 的可变编组动车组样车模型。2019年2 月,我国首列可变编组动车组完成全部60 余项厂内试验,具备出厂条件[4],可根据客流变化实现2 ~ 16 辆灵活编组。
在可变编组动车组的运行计划研究方面,陶若冰等[5]综合运用熵值法、变异系数法和BP 神经网络,研究可变编组列车不同座席的客流预测模型。姜安培[6]以运行图为输入参数,建立动车组运用优化模型。付建军等[7]提出可变编组动车组运用计划与检修计划一体化的思路,建立相应的混合整数规划模型,用改进的非支配排序遗传算法求解,采用帕累托前沿分析模型的2 个目标值。此外,还有一些学者研究城市轨道交通可变编组列车开行方案设计问题[8-10]。但是,目前我国针对可变编组高速铁路列车的开行计划优化研究较少。随着可变编组高速铁路动车组的研发、生产技术的完善,可变编组高速铁路列车将在更大的范围内应用,需要更新与变革相应运输组织工作。因此,研究高速铁路可变编组列车的开行计划优化问题,构建优化模型,设计分支定界算法,以确定列车需要进行组合、拆解作业的车站,以及各区段、各时段可变编组列车的编组内容,实现列车开行成本和乘客出行时间的最小化。
1 高速铁路可变编组列车开行计划优化模型
1.1 符号说明
高速铁路可变编组列车开行计划优化是在给定列车运行图和客流需求的条件下,确定各列车在各车站是否进行组合、拆解作业,以及各列车在各个区间运行时的具体编组内容[11]。高速铁路可变编组列车运行图为G= (I,A)或G= (I,P),运行图示意图如图1 所示。其中I= {1,2,…,R},是车站集合;1,2,…,R依次表示运行图下行方向车站编号,R为车站总数。A= {a1,a2,…,am…,aM}是区间运行线集合,P= {p1,p2,…,pn…,pN}是完整列车运行线集合,一条完整列车运行线由多条区间运行线组成。为了方便表述,将同一列车区间运行线am的后续紧邻的区间运行线定义为a′m,如p1= {a1,a2,a3},a′1=a2,a′2=a3。列车Wn表示在完整列车运行线pn上开行的列车。列车单元是由若干动车与拖车组成的不可拆分的列车组成单位,同类型及不同类型的列车单元之间均可进行组合或拆解以调整列车编组。列车单元与列车示意图如图2 所示。以2 种类型的列车单元U1和U2为例进行说明,U1列车单元由3 个车辆组成,U2列车单元由4 个车辆组成。模型集合与参数如表1所示。

图1 运行图示意图Fig.1 Train operation diagram
模型的决策变量xe(am)为正整数变量,表示区间运行线am上开行列车单元e的数量;yi(Wn) ∈ {0,1}表示列车Wn在车站i是否进行组合拆解,yi(Wn) =1 表示进行组合拆解,yi(Wn) = 0 表示不进行组合拆解。
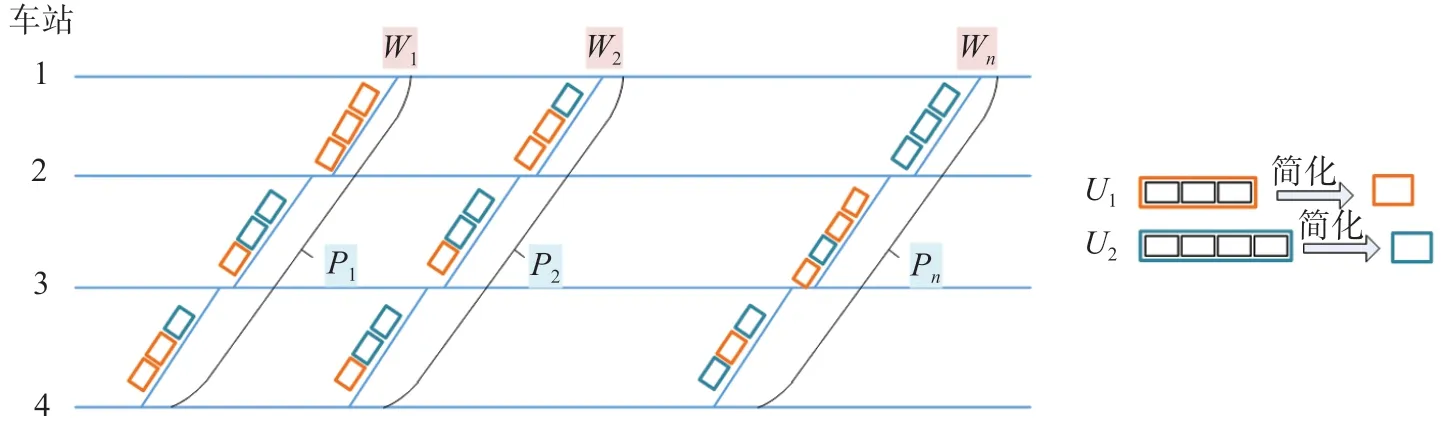
图2 列车单元与列车示意图Fig.2 Diagram of train unit and train
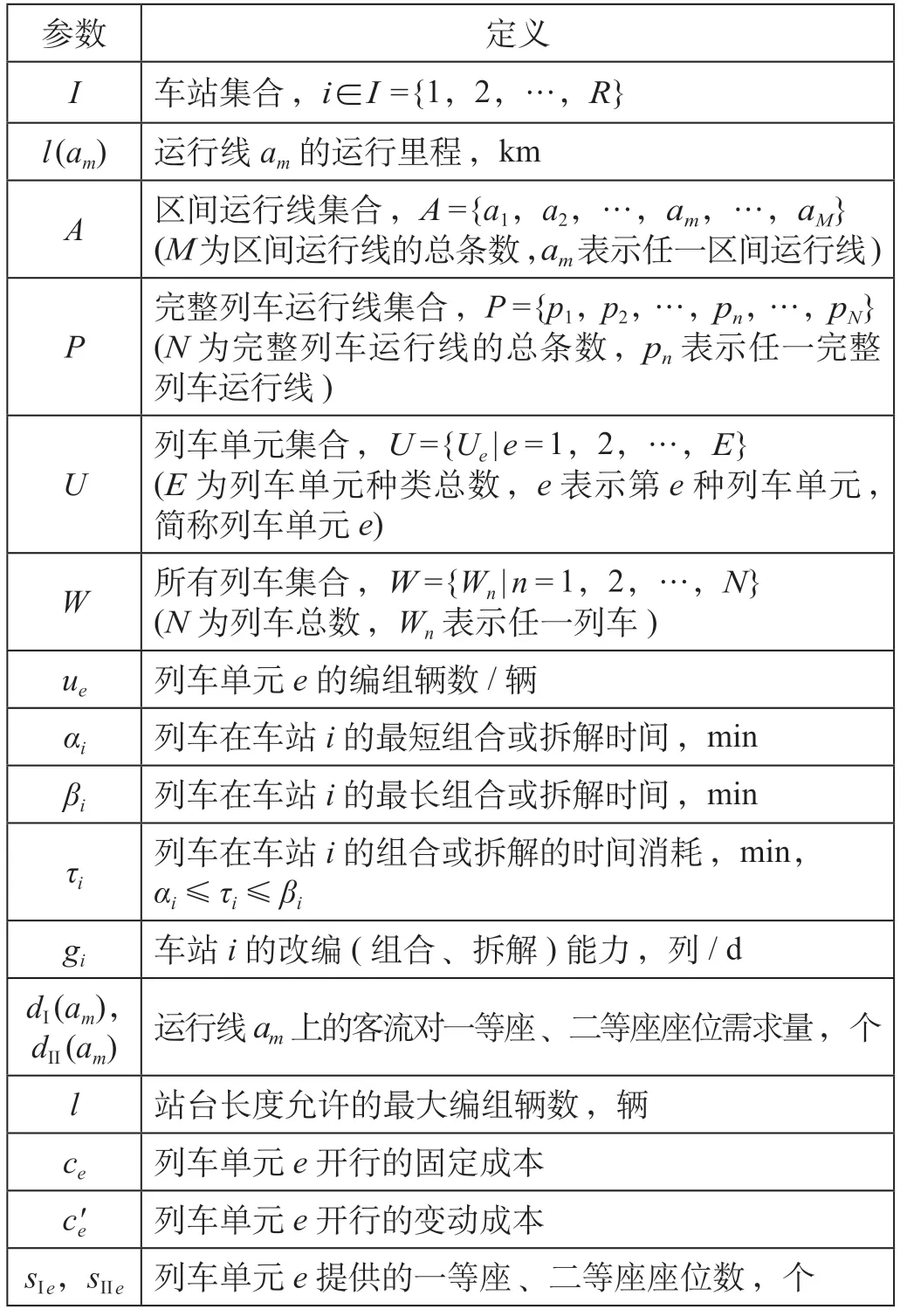
表1 模型集合与参数Tab.1 Sets and parameters of the model
1.2 数学模型
高速铁路可变编组列车开行计划优化模型以动车组开行成本(包括固定成本和变动成本)最小和组合拆解作业时间最短为优化目标,其中动车组开行成本是各区间运行线上各类型列车单元开行成本之和,固定成本是列车单元运行必须产生的成本,变动成本则与列车单元运行单位距离费用、列车单元数量和运行距离有关。目标函数为

模型具有以下约束条件。
(1)供给需求约束。在任一区间运行线am上开行列车单元所提供的一等座、二等座数量必须大于或等于相应的客流需求。

(2)站台容车约束。每个区间任何1 列车完成编组后的长度不可以超过站台长度。

(3)车站改编能力约束。每个车站每日安排的需要进行组合、拆解的列车不能超过车站的改编能力。

(4)决策变量关系约束。当同一列车在前、后紧邻区间的编组列车单元e数量不相等时,列车在这2 个区间的衔接车站i需要进行组合或拆解作业,反之则不需要组合拆解作业。
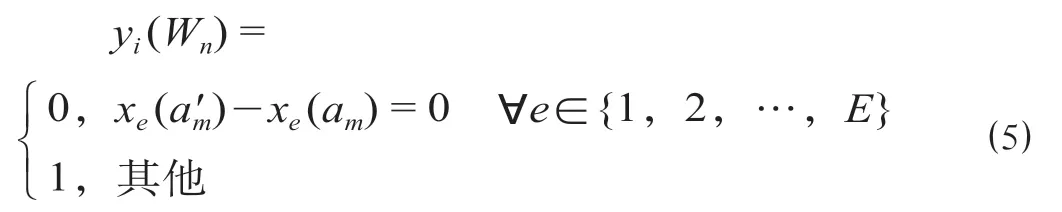
1.3 求解算法
以上模型是非线性整数规划模型,直接求解存在困难,因而采用分支定界算法并分两阶段进行求解。分支定界算法的基本思想是把原问题线性松弛后的可行域分解为范围越来越小的子域,并检查某子域内整数解的情况,直至证实整数解不存在或求出最优的整数解。令M1 (Xj)表示模型的1 个分支子问题,Xj为该分支上的子可行域。求解的步骤如下。
第一阶段:只考虑开行成本最小的目标及约束式(1)—(3)。
步骤1:初始化。先松弛问题的整数约束条件,求解其对应的线性松弛问题,如果线性松弛问题的最优解是整数解,则该整数解即为原问题的最优解。据此得出各车次在各区段、各时段所需要各类型列车单元的最小数量xe(am);否则,则将该线性规划解作为最优整数解的初始下界z-,并且设置初始上界z-为+∞。
步骤2:分支。分支是为整数解的出现创造条件。从任1 个子问题M1 (Xj)的不满足整数限制的变量中挑选1 个进行分析,通过加入1 对约束使子问题变为2 个带进一步约束条件的子问题。子问题的解若不满足整数解则继续进行分支,各分支可形成1 个倒立的分支树,分支树的根节点就是对应的线性规划松弛问题,它后面有2 个子节点,每个子节点后面可能又会有2 个节点,以此类推,直至此节点不可行或找到了1 个整数节点。各节点表示各子问题,若此问题已被求解过,则称此节点为封闭节点,未被求解则称为开放节点。
步骤3:定界与剪枝。定界是制定“过滤筛选条件”,剪枝就是根据“过滤筛选条件”来剔除不好的解。下界根据各开放节点中的最小目标函数值来确定,上界根据已找到的最优的整数解来确定,由此不断更新z-和z-。
步骤4:搜索迭代。每一次的分支过程即为一次搜索过程,在每次搜索中当上界被更新后,检查所有开放节点并封闭那些目标值大于新上界的节点。这一剪枝过程可以明显降低搜索和计算量。当所有节点被封闭时,则标志着所有搜索已完成,搜索过程中得到的最好整数解即为编组内容结果xe(am)。
第二阶段:根据第一阶段求解的结果,结合约束式(5)来判断组合拆解情况yi(Wn)。如果符合改编能力约束式(4),则算法结束,计算否则进入步骤5调整。
步骤5:对于不符合约束式(4)的yi(Wn)及相应的xe(am)进行调整,即如果某个车站每日安排的需要进行组合、拆解的列车超过了车站的改编能力,则取消该车站适当次数的改编作业(值最大的先取消),取消后相应的yi(Wn) = 1 变为yi(Wn) = 0,相 应 的xe(a′m) -xe(am) = 0,∀e∈ {1,2,…,E},返回步骤1。
2 案例分析
2.1 基础数据
京沪高速铁路全长1 318 km,共有24 个车站。考虑客流量情况,济南西、徐州东、南京南是京沪线上的3 个重要节点[12],因而重点考虑可变编组动车组在这3 个技术站进行站内组合拆解作业。因此,将北京南、济南西、徐州东、南京南、上海虹桥站这5 个车站作为本案例的研究对象,共形成4 个区段,4 个区段(按下行方向)的距离分别为406 km 和286 km,331 km 和295 km。在本案例中,考虑运行有种类型的列车单元,类型一是由2 动车1 拖车组成,类型二是由2 动车2 拖车组成,2 动车分别位于列车单元的首尾两端,设动车和拖车的长度相等。案例共设计29 个车次(98 条区间运行线),其中下行15 个车次(51 条区间运行线),上行14 个车次(47 条区间运行线)。根据可变编组客流预测研究结论[5],各车次及区间对座位的需求量(部分)如表2 所示。
2.2 求解步骤
设置站台长度约束下的所允许编组的最多车辆数量l= 16 辆;1 个类型一可变编组列车单元提供的一等座座位数sI1= 38 个;1 个类型一可变编组列车单元提供的二等座座位数sII2= 163 个;1 个类型二可变编组列车单元提供的一等座座位数sI2= 65 个;1 个类型二可变编组列车单元提供的二等座座位数sII2= 218 个。某车次列车在某区段某时段的一、二等座座位需求量dI和dII如表2 所示。车站的改编能力gi= 50 列/d。列车在车站的最短、最长组合或拆解时间分别为αi= 3 min,βi= 10 min。组合拆解作业时间按τi= 5 min 计算[13]。在开行成本方面,按车底数量比例进行折算,得到开行1 个类型一列车单元的固定成本和变动成本(即单位公里费用)分别为c1= 37 500 元,为c′1= 112.5 元,开行1 个类型二列车单元的固定成本和变动成本分别为c2=50 000 元,c′2= 150 元[14]。
将参数值代入模型,用分支定界算法求解得出各车次及区间需要的类型一和类型二列车单元的最小数量。以时间段6 : 35—13 : 57 为例,设计已知时刻表下可变编组列车编组情况(部分)如表3 所示。在列车的到、发时刻下方标出上文计算得出的所需2 种列车单元的数量。
将客座利用率(座位需求量/定员数)作为指标之一,分别计算可变编组下行和上行方向的客座利用率,并与固定编组进行比较分析(这里主要以二等座为例进行对比),得到可变编组与固定编组二等座客座利用率比较如表4 所示。固定编组列车即在列车运行全程不进行组合拆解作业。计算时,固定编组列车的编组内容由该车次运行线上客流量最大区间的客流需求决定,以保证供给满足需求。
可变编组与固定编组客座利用率对比如表5 所示。由表5 计算可得客座利用率优化的平均百分比为8.47%。

表2 各车次及区段对座位的需求量(部分) 个Tab.2 Demand of seats for each train in each section (Excerpts)
3 结束语
基于可变编组的高速铁路列车开行计划优化,对于提升高速铁路客运供需匹配和服务品质、提高动车组的运用效率、减少动车组的运用成本等方面都有着重要的理论和现实意义。针对可变编组的列车单元运用模式,构建可变编组高铁列车开行计划优化模型,在京沪高速铁路案例中应用上述模型,采用分支定界算法,求解得出可变编组列车在哪些站进行组合拆解作业以及各区段各时段的列车编组内容,并根据运行时刻绘制可变编组运行图,计算得出可变编组客座利用率相比同等条件下固定编组列车有较为显著的提高。但是,目前列车开行计划与运行图以及动车组运用计划尚未实现完全的一体化自动化编制,这也是未来的一个努力方向。
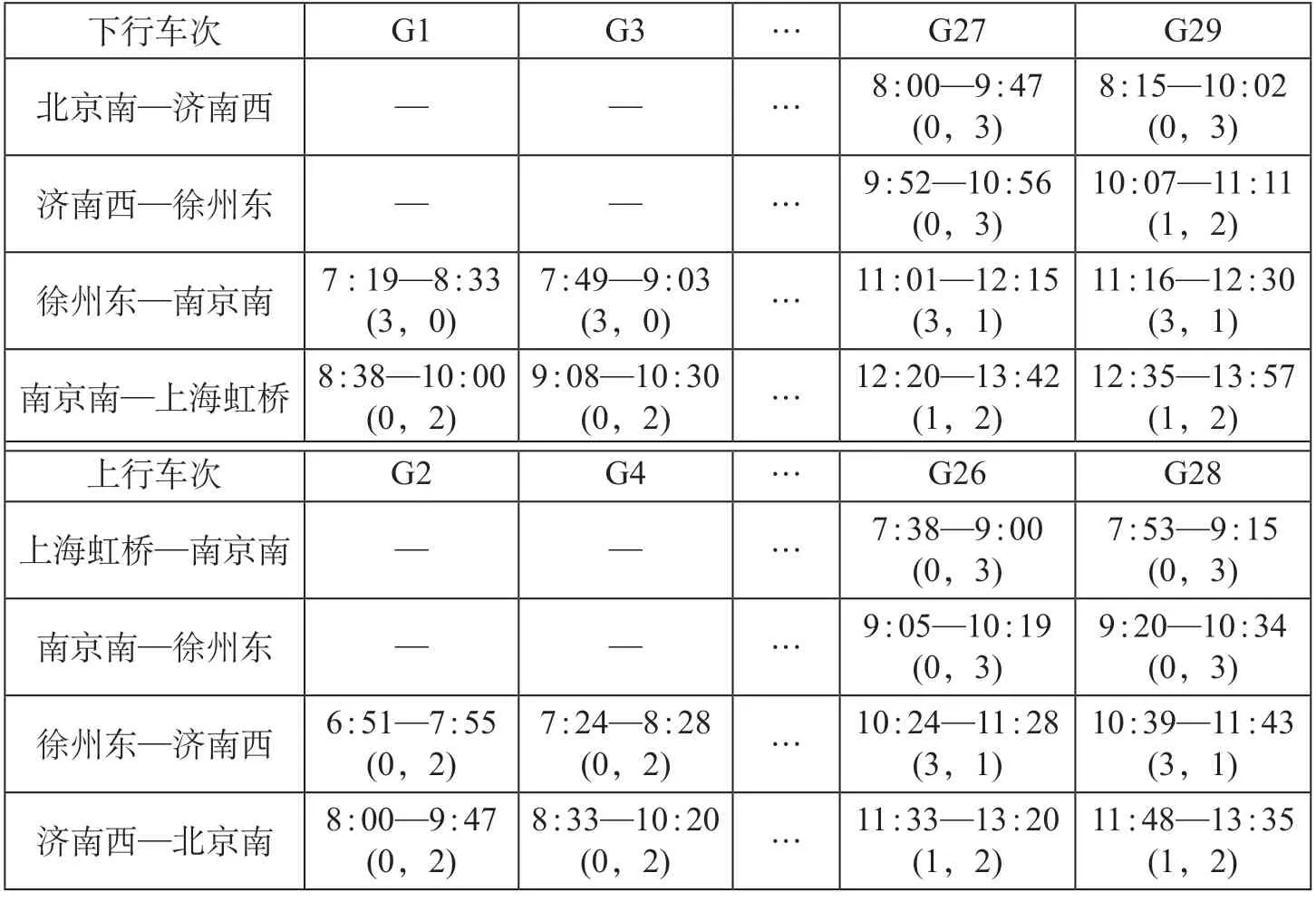
表3 已知时刻表下可变编组列车编组情况(部分)Tab.3 Marshalling content of variable configuration trains under the given timetable (Excerpts)
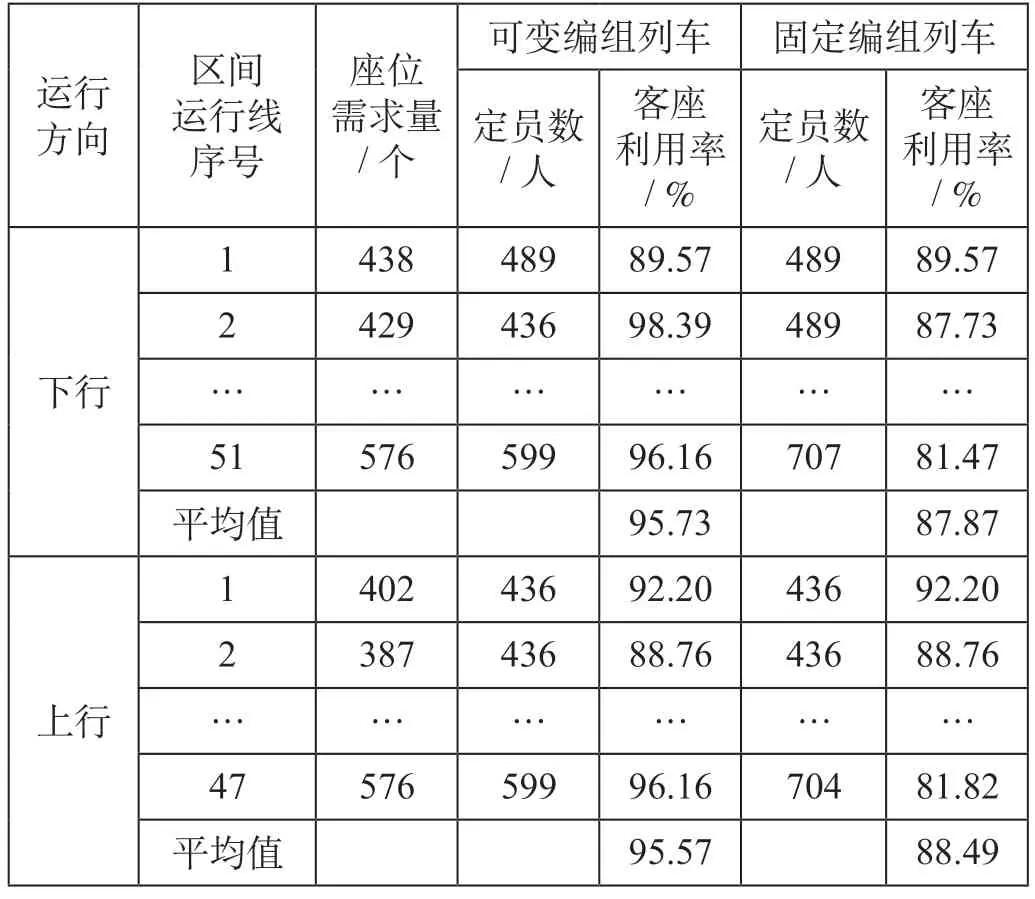
表4 可变编组与固定编组二等座客座利用率比较Tab.4 Comparison of load factor ratios for economy class between variable and fixed configuration train
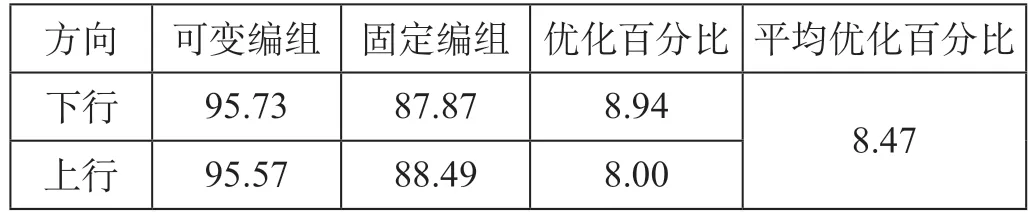
表5 可变编组与固定编组客座利用率对比 %Tab.5 Comparison of load factor ratios between variable and fixed configuration train
