考虑货物到达与列车出发时间接续的货物列车编成辆数研究

甘易玄，薛 锋，2，3

（1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 611756；3.西南交通大学 综合交通大数据应用技术国家工程实验室，四川 成都 611756)

0 引言

在我国铁路货物运输组织中，列车编成辆数主要由机车牵引定数或区段规定的列车长度决定，即通常所说的“满重满长”。随着铁路货运市场化的发展，为保证货物运到时限，在一定范围内可以适当采用“欠编欠轴”发车的组织方法。因此，灵活确定列车的编成辆数，对保障货物运到时限，提高货车周转效率，提升铁路货运市场竞争力具有重要作用。

目前，专门针对欠轴发车情况的货物列车编成辆数研究较少。Jonaitis[1]根据里程、效率、货运量之间的关系以及费用、列车运营效率、维修成本之间的关系提出2 种优化编成辆数的模型；Jeong[2]结合转运时间对运输成本的影响建立了开行方案优化模型；Kaspi 等[3]以最小运营成本和便捷度最高为目标，建立了开行方案的整数线性规划模型；王如义[4]分析了区段长度、车流量大小对最小编成辆数的影响规律，并给出最小编成辆数发车条件；崔园园[5]从运输收益的角度建立了放宽条件定点集结模式下最小编成辆数的区间确定模型；刘晨等[6]建立了放宽条件定点集结模式下的解体顺序优化模型，以最小编成辆数作为限定条件并采用遗传算法得到最优解体顺序；刘艳[7]建立了以运输企业效益最大和客户货运广义费用最小的双目标优化模型，确定了保本编成辆数及编成辆数可行区间；李静[8]建立了车辆在调车场集结过程的到达批服务排队模型，并从经济角度求得最优最小编成辆数。

列车编成辆数的确定不仅与列车开行后所产生的运行消耗有关，还与列车编成前的货物到达与编组的时间接续有关。为此，在考虑时间序列的基础上，构建基于接续时间的货物列车编成辆数波动模型，研究给定货物到达情况与列车图定发车时刻条件下编成辆数波动的列车配流方案，并分析最大、最小编成辆数与技术作业时间波动对发送货车数量及运输收益的影响。

1 基于接续时间关系的货物列车编成辆数波动模型

1.1 建模基本思路

基于接续时间关系的货物列车编成辆数波动模型以货物列车开行过程产生的运输企业经济效益最大为目标来确定编成辆数取值，除考虑货物列车开行收入与线路使用成本、牵引成本、车辆使用成本等各项基础成本支出的差值最大以外，增加货物到达与列车开行之间的接续时间所产生的接续等待消耗的影响；规定同一批货物只能分配至1 列满足接续要求的列车，且列车未集结至规定最小编成辆数时不能发车。

以此为基础，在考虑各项约束条件下，以运输企业经济效益最大为目标函数，结合货物到达和列车图定开行情况，得到编成辆数波动的货物列车配流方案，同时加入控制变量条件下最大、最小编成辆数，以及技术作业时间波动对发送货车数量和运输收益的影响分析。

1.2 符号说明

1.3 目标函数和约束条件

货物列车编成辆数的研究主要解决在非满轴发车时，如何实现提高货车周转效率的同时降低运输成本，以及如何根据货物到达与列车编组间的时间接续确定不同列车的编成辆数。

设Z 为货物列车开行过程产生的运输企业经济效益，且定义决策变量mk和yik，考虑3 个方向的货物运输，即Ln中n = 1，2，3。根据不同批次货物对应编成的列车辆数以及决策变量yik决定的第i批货物是否能够分至第k 列车，并结合《铁路货物运价规则》制定的运费计费规则得到货物列车开行收入Z1如下。

同时，铁路货物列车开行产生的运输成本如下。

由第k 列列车编成辆数与该列车运行路径公里所决定的线路使用成本Z2为

由机车牵引货运列车产生的成本支出，模型中考虑机车自重以及列车编成辆数决策下自重所带来的单位吨公里牵引成本消耗Z3为

在确定第k 列列车的编成辆数后，由列车开行方向的路径公里以及列车运行速度决定列车运行时长，从而得到车辆总使用成本Z4为

根据中国国家铁路集团有限公司相关规定，特快及快速货运班列开行要额外产生成本费用，利用θk作为0-1 变量控制第k 列列车种类，若为特快及快速货运班列则此项计入总成本，否则不计入，故特快及快速货运班列开行额外产生成本费用Z5为

由货物列车在发站、到站进行发到作业而产生的成本支出Z6为

由第k 列列车发出时间与第i 批货物到达时间之间的接续时间所产生的接续等待时间费用Z7为

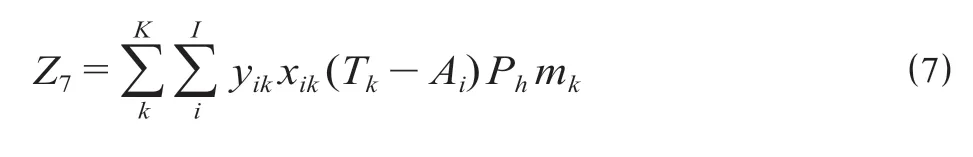
综上所述，货物列车开行过程产生的运输企业经济效益Z 为

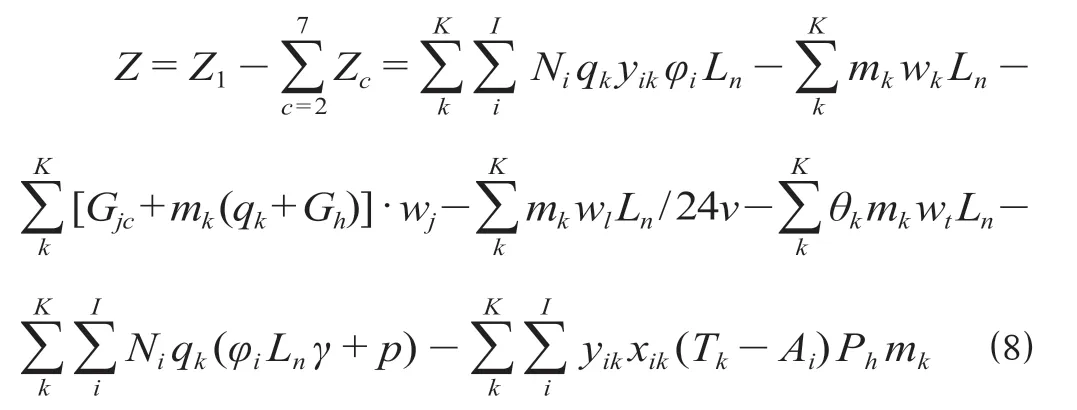
为确保模型的可行性，采用欠轴发车提升运输效率的同时，运输企业经营收益始终不小于零，故运输企业经济效益Z 存在以下约束。

考虑在欠轴条件下，列车编成辆数不能无限制增大和减少，故依据区段通过能力制约，编成辆数大小存在区间限制，即

在列车载重约束方面，限制列车载重吨数不超过列车最大运输量

公式(7)中xik为0-1 变量，由货物到达时间、车站技术作业时间以及列车出发时间决定，若到达的一批货物与列车开行方向一致，且货物到达、车站技术作业完成后仍未到列车发车时间则xik取1，接续时间消耗计入成本；若到达的一批货物与列车开行方向不一致或者货物到达并进行车站技术作业后的时间已大于列车开行时间，则xik取0，无接续时间成本消耗。

同一批货物只能分配至1 列满足接续要求的列车

由第i 批货物的车辆数以及决策变量yik决定的每列列车的车流来源存在如下约束条件

对于编成辆数，发车条件存在最小编成辆数约束

对于编成辆数，当ck= 0 时，mk必为0。

结合公式(1)至公式(16)便得到基于接续时间关系的，以铁路运输企业经济效益最大化为目标函数的货物列车编成辆数波动模型。

1.4 模型求解

针对构建的货物列车编成辆数波动模型，提出模型求解步骤如下。

步骤4：经步骤3 后，模型中的约束条件为公式(9)至公式(11)、公式(13)至公式(16)，目标函数不变同公式(8)。此时该模型为混合整数线性规划模型，可调用软件求解。

2 算例分析

2.1 参数输入

考虑3 个路径方向的货物运输，货物到达情况如表1 所示。合计到达45 批货物，货物到达信息包括货物到达时刻Ai、货物对应的所需装车数Ni以及货物对应的发送路径编号Di(1)。列车开行径路及发车时间如表2 所示。对于前一天未发出的列车已按照其列车到达情况加入到达列车列表，无需另作考虑。此外，规定最大编成辆数M1= 60 辆，最小编成辆数M2= 45 辆。该模型针对的是一次改编作业，当货物运输需经过多次改编时，以货物途经改编站作为新的研究技术站，重复调用该模型可完成需经多次改编的货物运输。

表1 货物到达情况Tab.1 Arrival of freight

2.2 列车配流方案分析

以运输企业经济效益最大化即公式(8)为目标，利用公式(12)简化模型后结合公式(9)至公式(11)、公式(13)至公式(16)进行求解。基于软件平台编程，求解该混合整数线性规划优化模型，得到车流来源及列车编成辆数情况如表3 所示。其中货物发送收入结合公式(1)为Z1= 2 165 353 元，货物发送各项成本结合公式(2)至公式(7)为货物发送净收益结合公式(8)为Z= 572 235 元。

计算结果显示，研究时段内到达货车1 245 辆，实际发出货车1 245 辆，实际开行列车23 列且由于公式(10)与公式(15)对应列车编成辆数上下限约束，故求得各列车的编成辆数mk均位于区间[45，60]之内。其余22 列列车由于列车开行情况和货物到达情况的限制，未能达到产生开行收益的最小编成辆数或是未能实现同一批货物的不拆车运行，从而导致停开，这表明列车编成辆数不能无限制减少；若这些列车均按图定时刻开行，虽能加速货物运送却会造成运输企业的亏损。因此，货物到达与列车编组的接续时间关系会直接影响列车编成辆数和列车配流方案的确定。另外，由于快运列车开行收益高于一般列车，故求得方案中快运列车的编组辆数高于一般列车编组辆数。该方法与现有的组织方式相比，仅改变了允许开行列车时的编组辆数要求，没有改变既有的车站作业秩序和步骤，有较高的可实施性。

表2 列车开行径路及发车时间Tab.2 Train operation route and departure time

表3 车流来源及列车编成辆数情况Tab.3 Source of traffic flow and number of marshalled trains

2.3 影响因素分析

（1）最大编成辆数影响分析。最大编成辆数对发送货车数量及货物运输收益的影响如图1 所示，其表示在最小编成辆数不变的条件下发送货车数量和货物运输收益随最大编成辆数的变化情况，其中，最小编成辆数M2取45，图1 显示，最大编成辆数与发送货车数量以及货物运输收益均呈正相关，由此表明列车编成辆数的允许数值范围越大，列车能够运送的货物越多，运输企业经营效益越高。

（2）最小编成辆数影响分析。最小编成辆数对发送货车数量及货物运输收益的影响如图2 所示，在最大编成辆数M1取60 且保持不变的条件下，随着最小编成辆数的不断增大，发送货车数量和货物运输收益呈下降趋势。最小编成辆数越大则开行条件越接近满轴，根据图2 所示，当最小编成辆数为55 时发送货车数量和货物运输收益均为图2 中最低值，故按照现有满轴开行列车的规定并不能给铁路运输企业带来最高的运输效益。当最小编成辆数在[35，45]范围内，发送货车数量和货物运输收益处于较为可观的位置，故在保证最大编成辆数不变的条件下，采用欠轴发车35 ～ 45 辆能够实现同时提高货车周转效率和经济效益。

图1 最大编成辆数对发送货车数量及货物运输收益的影响Fig.1 Influence of the maximum number of marshalled vehicles on the quantity of the departure wagons and the revenue of freight transportation

图2 最小编成辆数对发送货车数量及货物运输收益的影响Fig.2 Influence of the minimum number of marshalled vehicles on the quantity of the departure wagons and the revenue of freight transportation

（3）技术作业时间波动影响分析。在车站完成技术作业的标准时间基础上，对其设定一定的波动率，以分析技术作业时间波动对货物运输收益以及发送货车数量的影响。技术作业时间波动率对发送货车数量及货物运输收益的影响如图3 所示。当技术作业时间波动率在[0.8，1.0]，[1.1，1.4]和[1.6，1.9]之间时，技术作业时间对货物运输收益以及发送货车数量的影响基本稳定，但随着波动率的不断增大，2 项指标整体均呈现下降趋势。因此，车站完成各项技术作业的时间应尽量不超过规定基础时间的1.4 倍，同时因技术站作业不确定性导致的车站作业时间大量延长或缩短并不利于提升货物运输收益及发送货车数量。

图3 技术作业时间波动率对发送货车数量及货物运输收益的影响Fig.3 Influence of the volatility of technical operation time on the quantity of the departure wagons and the revenue of freight transportation

3 结论

通过考虑货物到达情况与列车图定发车时刻间的接续关系，构建基于接续时间的货物列车编成辆数波动模型，研究给定货物到达情况与列车图定发车时刻条件下编成辆数波动的列车配流方案。在此基础上，对最大编成辆数、最小编成辆数、技术作业时间波动等指标对发送货车数量及货物运输收益的影响进行分析，主要研究结论如下。

（1）货物到达与列车编组的接续时间关系会直接影响列车编成辆数和配流方案的确定。

（2）列车编成辆数的允许数值范围越大，列车能够运送的货物越多，运输企业经营效益越高。

（3）满轴开行列车并不能给运输企业带来最高的运输效益，本算例在列车最大编成辆数不变的条件下，采用欠轴发车35 ～ 45 辆货运效率和经济效益都更为显著。

（4）车站完成各项技术作业的时间不应超过规定基础时间的1.4 倍，同时因作业不确定性而导致作业时间大量延长或缩短不利于提升发送货车数量及货物运输收益。