气井井筒条件下单液滴动力学特征及其携带临界气流速

王志彬 张亚飞 孙天礼 李忠城 杨中位 朱国 石红艳

1. 西南石油大学油气藏地质及开发工程国家重点实验室；2. 中联煤层气有限责任公司；3. 中石化西南油气分公司采气二厂；4. 中石化西南油气分公司基建部

0 引言

气井连续携液临界气流速是排水采气工艺优化设计的重要参数［1］。携液生产气井井筒中流型为环状流，一部分液体以液膜形式沿管壁流动，一部分液体以分散液滴形式被气流夹带。液膜及液滴的携带临界气流速直接影响环状流场中液体连续携带的临界气流速。为此，气井携液临界气流速计算出现了液膜携带模型和液滴携带模型两大学术派别。

液滴模型认为井内最大液滴回落是导致气井积液的首要因素。1969年Turner等［2］率先建立了单液滴携液模型，该模型假设液滴为圆球状，液滴曳力系数和破碎韦伯数分别取为0.44和30，并认为若气流能将环状流场中的最大液滴带出井口，则气井不会积液。Turner单液滴模型因简单，便于计算，四十年来被各大油田广泛应用。然而在工程应用中发现，很多气井携液产气量与Turner模型预测值相差较大，为此国内外学者对气井连续携液理论开展了大量的研究工作。Coleman等［3］、Nosseir等［4］、李闽等［5］、周德胜等［6］、王志彬等［7-12］分别考虑油压、流型(层流或湍流)、液滴群聚效应、液滴变形、液滴翻滚、界面张力等因素的影响，先后建立了各种液滴携带新模型。目前几乎国内各大气田根据生产数据拟合了适合本气田的携液流量计算经验模型，可见携液规律之复杂。

气井井筒高温高压条件下液滴的动力学特征，尤其是液滴的形状特征、曳力系数以及与液滴尺寸有关的临界韦伯数未见相关报道，这给准确分析液滴携带规律带来了难度。这些参数可通过实验测量，也可通过建模计算。气井井筒高温高压下的实验测试成本高、难度大，为此，笔者选用了数值模拟方法。

液滴形状特征和曳力系数的获取有3种数值模拟方法。第1种是将液滴置于大的计算区域中，让气流吹液滴直至液滴变形达到稳定［13-14］，或允许液滴在较高垂直密闭气柱中自由下落［15］，该方法网格数量和计算量大。第2种是液滴界面追踪法，该方法应用动网格捕捉界面特征［16］。第3种是施加体积力使液滴保持恒定的相对速度或固定在恒定位置［17-18］，该方法仅需要局部细化液滴及其周围区域，可以大大减少计算量。同时，目前液滴动力学特征研究主要集中在雷诺数小于200，而对气井井筒条件高雷诺数下的液滴动力学特征鲜有研究。

笔者建立了描述湍流场中液滴动力学特征的数值模型，开发了液滴动力学特征模拟求解器；计算了不同韦伯数下的液滴形状特征、曳力系数及液滴破裂的临界韦伯数；对液滴进行受力分析，得到液滴携带所需要的临界气流速预测新模型；利用文献数据对现有单液滴模型进行了适应性评价，给出了单液滴模型适用的产液量条件。

1 单液滴动力学模型

1.1 数学模型的建立

1.1.1 基本方程

因计算区域较小，气体的密度可考虑为常数。施加在流体上的力包括重力、表面张力和黏性应力。不可压缩、黏性、不相溶流场的控制方程描述如下［19-21］

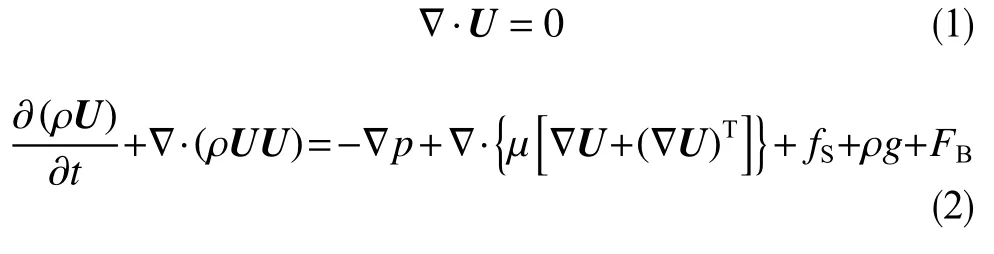
式中，U为笛卡尔坐标系中的速度矢量，m/s；p为压力，Pa；t为时间，s； ∇·为矢量发散算子；∇为标量梯度算子；fS为界面处由表面张力引起的体积力，N；ρ为密度，kg/m3；μ为黏度，Pa · s；FB为以源项形式添加的体积力，N；g为重力加速度，9.8 m/s2。

气液界面形状是研究的重点，本研究使用流体体积函数法(VOF)研究气液界面结构。对于相分布计算，在空间中采用体积函数α来识别网格中的组分。定义如下：对于充满气相的网格单元，αL=0；对于气液界面处的单元，0＜αL＜1；对于充满液相的单元，αL=1。

计算单元中的混合物理性质可以由体积分数的值计算

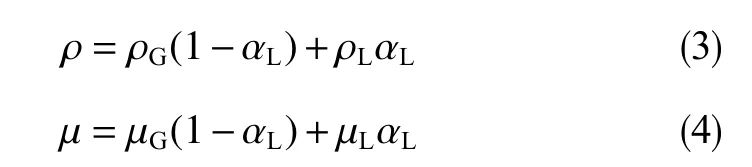
气液表面张力会产生一个额外压力梯度力，使用CSF模型［22］对每单位单元体积进行评估。

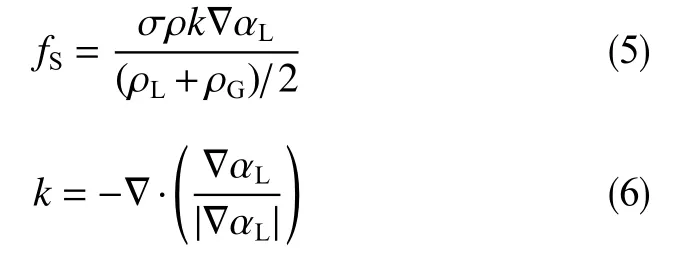
式中，σ为气液界面张力，N/m；k为自由表面的平均曲率；下标L、G分别代表液相和气相。

1.1.2 液滴曳力系数计算式

液滴在其自身重力和曳力的作用下加速或减速，作用于液滴的曳力可以通过液滴的计算网格积分得到。根据高斯定理，体积积分可以转化为面积分。在本研究中，气流沿y方向流动，即从底部向上部流动，由于液滴周围气流场呈对称分布，故曳力垂直向上。所以y方向上的曳力可通过下式积分得到。

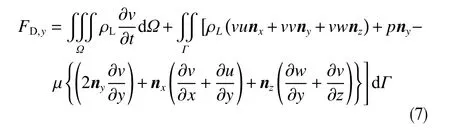
式中，Ω为液滴控制体；Γ为液滴控制体的表面；nx、ny、nz为垂直于液滴表面的单位矢量；u、v、w为x、y、z方向的速度分量。

由式(7)可知，总曳力系数由4部分组成或产生4种作用。一是使液滴加速，二是促使液滴内部循环(由于液滴内部存在速度梯度使得液滴变形和内部循环)，三是来自液滴迎风面和背风面之间的压差，最后是克服液滴表面摩擦的黏滞阻力。后3项是通过对液滴表面单元进行微分来计算的。在式(7)中，nxΓcell、nyΓcell、nzΓcell(Γcell是表面单元面积大小)实际是液滴表面在x、y、z方向上的投影面积，可以通过相分数梯度和单元体积计算得到。

液滴前后压差产生的曳力可以简化为

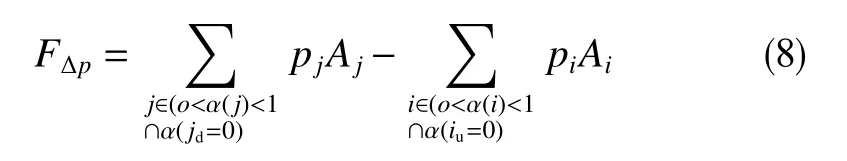
由体积力计算液滴的总曳力系数为

式中，pjAj为施加在液滴迎风面的单元(j)上的压力，N；piAi为施加在液滴背风面单元(i)上的压力，N；iu、jd分别为液滴表面上方和下方单元，对于该单元，相分数α=0；Af为基于液滴初始直径迎风面面积，m2；Af为基于液滴初始直径迎风面面积，m2；D为液滴的初始直径，m。

1.1.3 体积力计算式

为了避免液滴加速或减速对液滴曳力模拟准确性的影响，同时减小模拟计算工作量，本研究中对液滴施加了体积力以使其保持在恒定的位置。体积力在每个计算时间步中根据牛顿第二定律计算。

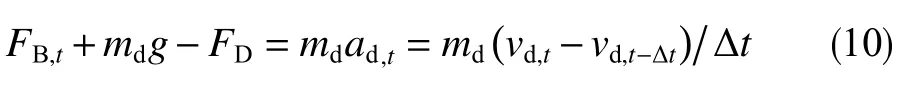
由于每个计算时间步长的液滴质心速度等于0，所以式(10)中vd,t-Δt=0，则式(10)可简化为

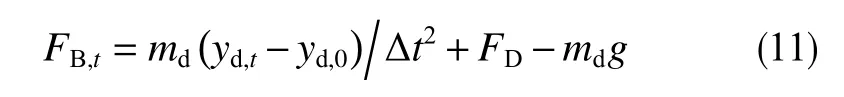
yd,0是y方向上的初始质心，yd,t是当前时刻y方向的质心，由下式计算

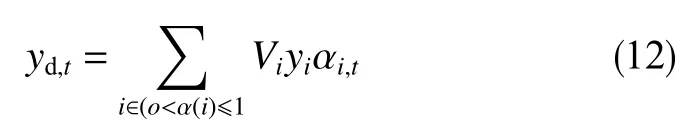
式中，md为液滴质量，kg；ad,t为在体力FB,t作用下液滴当前时刻t的加速度，m/s2；vd,t，vd,t-Δt分别为当前时刻t和之前计算时刻t-Δt的液滴质心速度，m/s；Vi为单元(i)的体积，m3；yi为单元(i)在y方向上的质心，m。

事实上，FD未知，质心中心yd,t是体力FB,t的隐式函数。

牛顿迭代法被用来计算体积力，计算式为

yd,t是在上一体积力FB,t,old条件下液滴质心在y方向的位置，FB,t,new是当前体积力，grad(yd,t)是液滴质心位置yd,t对体积力FB,t,old的变化梯度。

在获得体积力后，瞬时曳力可以由式(15)计算

当前时间步的瞬时曳力系数为

根据Prahl等(2006)［15］的研究，人工重力对液滴变形和破裂的影响可以忽略不计。

1.2 数学模型的求解

式(1)和式(2)使用有限体积法进行离散。瞬态项和源项使用中心差分进行离散并沿单元体积进行积分。应用高斯定理将扩散项和对流项差分转化为单元体表面积分，单元面的值利用Van Leer通量限制求解。通过面积分来计算单元体的值，计算单元面的值通过插值计算。采用Jasak(1996)［23］和Waterson等(2007)［24-25］的求解方案就对流项进行离散处理。此外，时间微分项使用隐式Euler方法进行离散，该方案无条件稳定，一阶时间准确，并保证解的有界性。相函数使用有限体积法进行离散化处理，并对整个单元体积和时间进行积分。面插值从相邻计算单元的值计算得到。

纸条的疑问是在毕业四年后我结婚那天才得到解答的。那天我的许多老同学都来了，当然有邓军、胡波、赵小明这三个死党。

整个求解过程基于PIMPLE算法总结如下：(1)在每个计算时间步骤之前保存所有初始场，包括速度u0、压力p0、体积分数α0；(2) 求解相分数方程式(3)获得更新的体积分数场；(3)通过式(4)和式(5)更新流体性质；(4) PIMPLE动量压力耦合算法更新速度和压力场；(5)用牛顿迭代程序计算体积力：①从u0、p0、α0等3个初始场参数恢复初始场；②使用PIMPLE算法计算新的速度和压力场；③修正曳力；④计算液滴质心位置；⑤重复步骤①～④，直到前后2次计算的液滴质心位置满足精度要求；(6)计算体积力；(7)计算曳力和曳力系数；(8)返回步骤(1)，并计算下一新的计算时间步的流场信息。基于以上求解过程，开发了单液滴动力学特征模拟器。

1.3 物理模型及网格划分

在连续均匀速度场中放置一个液滴，计算域是一个边长为64D的立方体，如图1所示。将液滴置于计算域的中心。通过施加体积力将液滴保持在恒定位置，体积力由液滴的加速度计算得到。计算初始时刻，液滴初始形状为球状，直径为D。入口为速度边界，出口是压力边界。网格用七级局部加密，最大网格长度等于液滴直径，最小网格长度为液滴直径的1/32。

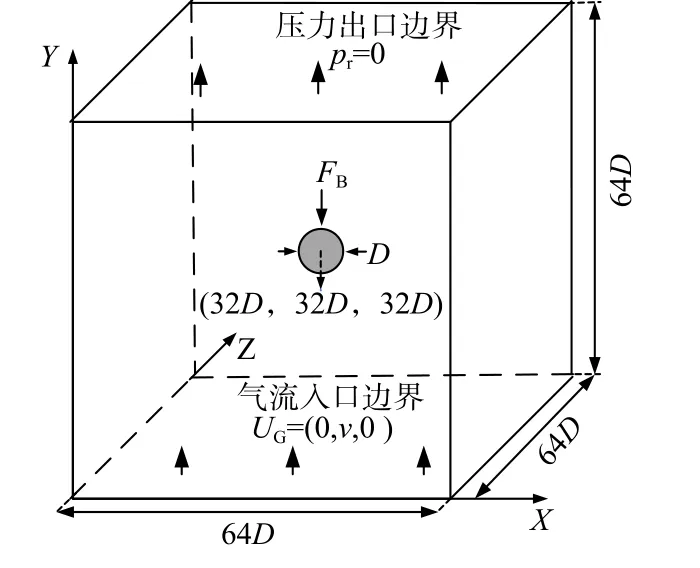
图1 物理模型Fig. 1 Physical model

为了确定网格分辨率或者网格尺寸对模拟结果的影响，设计了3种网格局部加密方案，分别采用5、6、7级局部网格，最细的网格尺寸分别为液滴尺寸的1/16、1/32和1/64(图2)。在韦伯数We=1.1和雷诺数Re=1 150的条件下，测试了网格加密对曳力系数的影响。图3为曳力系数随时间的变化。显然，随着网格局部加密级数的增加，曳力变得更加连续和稳定。六级加密方案结果与七级加密方案结果之间的差异很小。因此，本研究的所有案例都采用六级网格局部加密方案。

图2 网格局部细化方案Fig. 2 Local grid refinement scheme

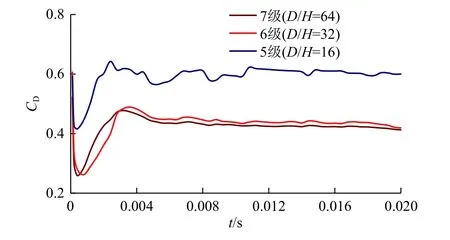
图3 网格加密级数对曳力系数的影响(We=1.1，Re=1 150)Fig. 3 Influence of grid refinement grade on drag coefficient(We=1.1，Re=1 150)

1.4 模型准确性验证

Reinhare(1964)［25］测量了空气中下落水滴的终极曳力系数CD和椭球度E(液滴高度与液滴变形后横向直径的比值)，Loth(2008)［26］对其实验数据进行拟合，提出曳力系数和椭球度经验式。根据Reinhare(1964)的实验条件，拟定了本次数值模拟的物性参数：气液界面张力0.07 N/m，液滴尺寸4 mm，液体黏度2.0×10-4Pa·s，气体黏度1.67×10-5Pa·s，液体密度1 000 kg/m3，气体密度1.2 kg/m3。气流速和对应的韦伯数We及液滴雷诺数Re、数值模拟得出的曳力系数CD和椭球度E与测试值对比如表1所示。曳力系数的平均绝对百分误差为9.98%，椭球度的平均绝对百分误差为11.45%。除韦伯数为11.95时模拟得到的椭球度0.24远小于实验测量值0.32，其他模拟椭球度均与实验测量值吻合。同时，Quan等(2006)［16］和Helenbrook等(2002)［17］在韦伯数为12条件下椭球度模拟值为0.2，与当前模拟值非常接近。

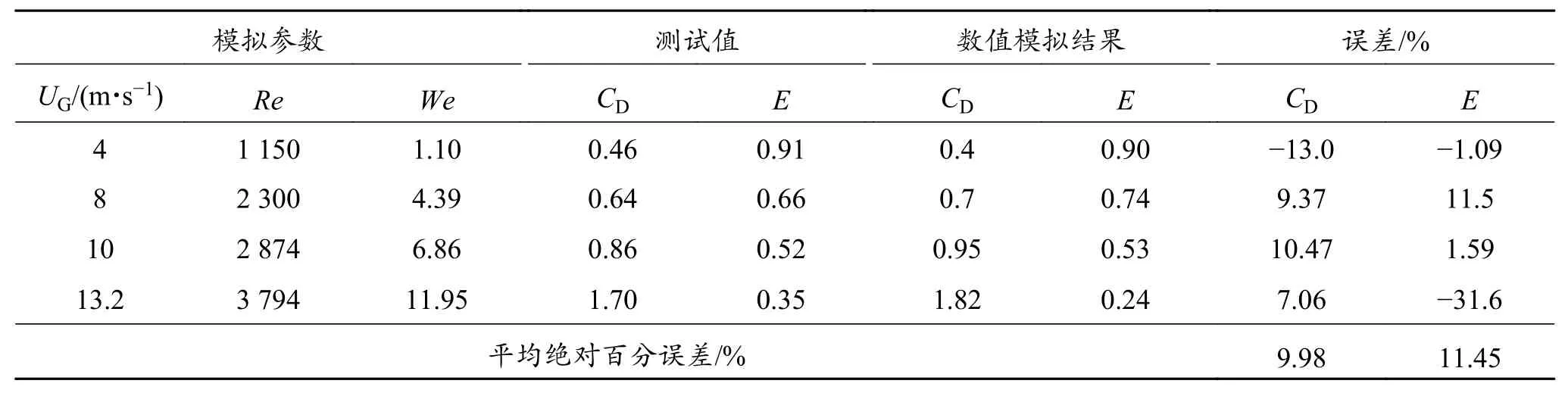
表1 模拟结果与实测值对比Table 1 Comparison between simulation results and measurement values

图4对比了Reinhare (1964)［25］实验测量的空气中下落水滴的形状和本文模型数值模拟的液滴形状，可以看出，两者形状非常吻合。

图4 测量液滴形状与模拟液滴形状对比Fig. 4 Comparison between measured drop shapes and simulation results

2 气井井筒条件下单液滴动力学特征

2.1 物性参数

某气井井底流体压力为4 MPa、温度为353 K。根据高温高压物性计算方法，气液界面张力取0.05 N/m，液滴尺寸4 mm，液体黏度3.6×10-4Pa·s，气体黏度1.24×10-5Pa·s，液体密度972 kg/m3，气体密度27.1 kg/m3。气流速分别取0.68、1.36、1.78、2.36 m/s，对应的韦伯数为1、4、6.8、12.1，对应的液滴雷诺数Re为594、1 171、1 556和2 063。

2.2 液滴变形及破碎规律

从图5可看出，在韦伯数为1时，可观察到比较显著的变形。随韦伯数增加，液滴变形程度增加，液滴椭球度增加，逐渐变形为扁平体。当韦伯数增加到12.1时，扁平体在纵向上变得很薄，形状类似于 “馕饼”；由于气流的作用，“馕饼”向内凹陷，并发展成中空的袋状，最后破碎，如图5(d)所示。模拟中发现液滴破碎的临界韦伯数约12，该值与低雷诺数条件下实验测试或数值模拟值［16］接近，为此，气井井筒条件下液滴破裂的临界值可取12。

图5 不同条件下单液滴变形过程模拟Fig. 5 Simulated deformation process of single drop under different conditions

2.3 液滴曳力系数

图6给出了对应韦伯数条件下液滴曳力系数及椭球度随时间的变化过程，可以看出，韦伯数等于1时，液滴的曳力系数从0.42逐渐增加，最后稳定在0.57；韦伯数等于4时，液滴的曳力系数从0.36逐渐增加，最后稳定在0.76；韦伯数等于6.8时，液滴的曳力系数从0.39逐渐增加，最后稳定在0.97；韦伯数等于12.1时，最大曳力系数在液滴破碎时刻，此时液滴迎风面积达到最大，气流所施加的曳力最大。对于韦伯数略小于12的液滴，液滴仅变形但不破碎，根据图6(d)中曳力系数随液滴变形程度的变化规律，曳力系数稳定在1.3附近，变形达到稳定阶段，因此建议曳力系数取1.3。不同韦伯数下液滴变形达到稳定后的曳力系数分析表明，液滴变形达到稳定后，最终的曳力系数随韦伯数增加而增加。

根据标准曳力系数(Reinhare，1964)［25］，即不变形固体颗粒的曳力系数，当液滴雷诺数Re＞1 000时，固体球体的曳力系数为0.424，与韦伯数为1的模拟值吻合很好。同时，根据Rodi等(2002)［27］提出的液滴加速状态下的曳力系数计算式，Re＞1 530时的曳力系数为2.62，略大于当前数值模拟的曳力系数1.70。这里，标准曳力系数0.424既不包含加速度作用也不包含液滴变形作用对曳力系数的影响，而2.62包括了这2种作用的影响，而本次数值模拟仅考虑了液滴变形作用的影响。因此，对于韦伯数低于临界韦伯数的情况，液滴变形稳定后曳力系数介于标准曳力系数和加速状态曳力系数之间，液滴加速将使曳力系数增加。

3 单液滴携带临界气流速计算模型

数值模拟得到的液滴曳力系数、临界韦伯数为液滴携带临界气流速研究提供了重要基础参数。

3.1 模型的建立

气井中的液滴主要受自身重力、气流对液滴的曳力和浮力作用。由液滴质点受力可知，当气流速足够大，液滴将悬浮在气流中，此时重力等于浮力与曳力之和，即满足式(17)。

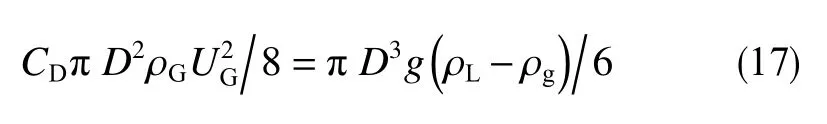
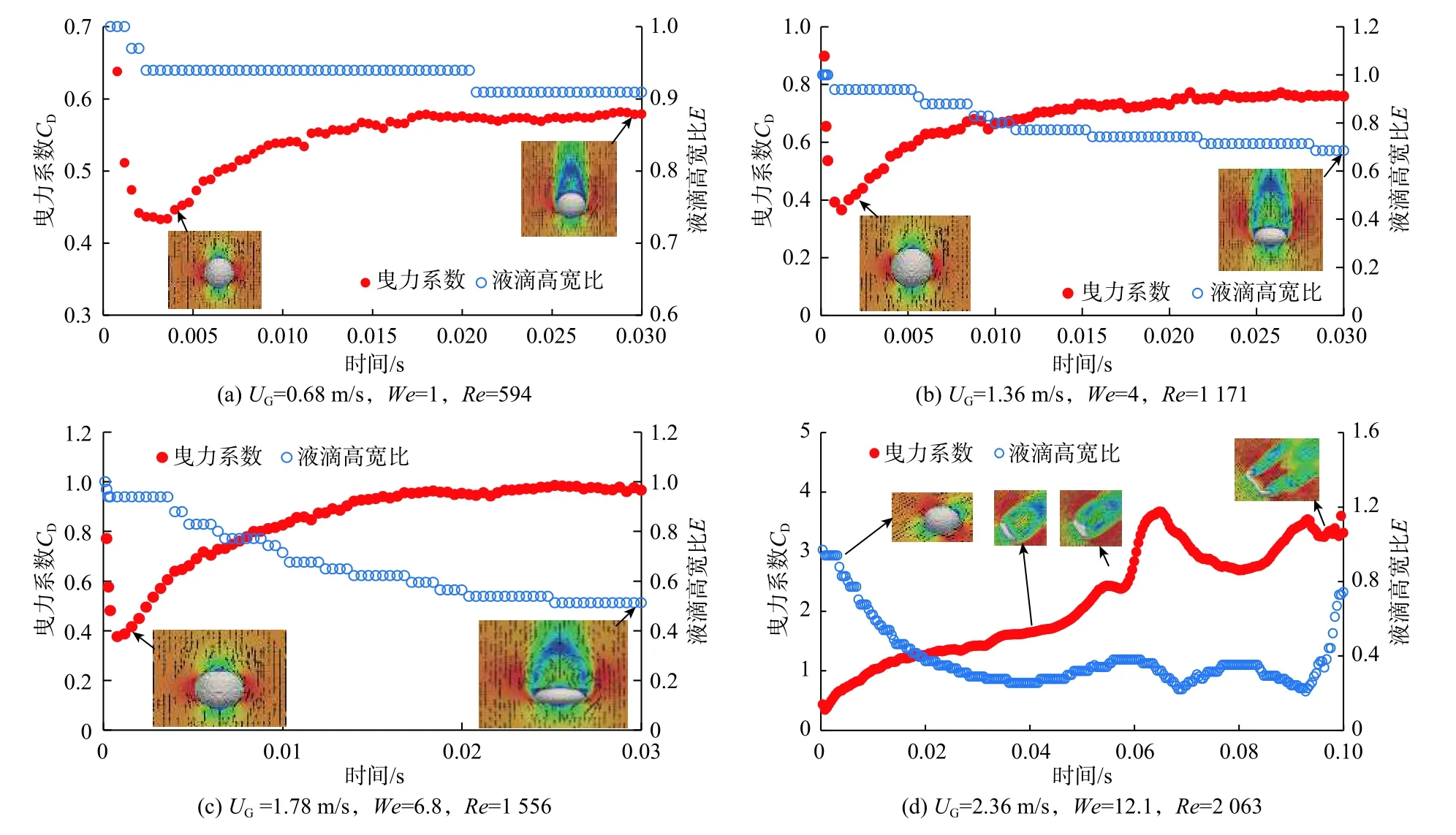
图6 液滴曳力系数CD随时间的变化Fig. 6 Variation of drop drag coefficient (CD) with time

其中，C定义为液滴携带临界气流速综合系数，表征液滴尺寸和液滴变形对液滴携带临界气流速的影响。

根据模拟得到的液滴在不同韦伯数下的曳力系数，计算了不同韦伯数下的综合系数C。从表2可知，气流场中不同韦伯数下临界气流速综合系数在2.19～3.31之间变化，综合系数取3.31计算得到的流速可将流场中所有大小液滴带走。

Turner模型假设液滴为圆球状，将液滴曳力系数和临界韦伯数分别取为0.44和30，所得的系数为5.5，为安全起见，Turner模型将系数上调20%，最后建议系数为6.5。Coleman认为在低压气井条件下，该系数可不上调，建议系数取5.5。李闽假设液滴为椭球体，将曳力系数取为1，最终的模型系数为2.5。结合本研究的数值模拟结果来看，Turner模型和Coleman模型的综合系数偏保守，所计算的气井携液临界气流速是液滴携带所需临界气流速的1.96倍和1.76倍。李闽模型所计算的气井携液临界气流速与液滴携带所需临界气流速接近。

表2 不同韦伯数下的液滴携带气流速综合系数Table 2 Composite coefficient of drop carrying gas flow rate at different Weber numbers

但是，从携液模型的应用来看，Turner模型和Coleman模型在国内外大液量气井广泛应用，而李闽模型在国内低渗低液量气井广泛认可。从气井井筒携液机理的角度分析，大液量气井的积液本质是液膜回流，气井连续携液临界气流速由液膜携带的临界气流速控制，液膜携带的临界气流速比液滴携带的临界气流速大得多，而低液量气井连续携液临界气流速由液滴携带的临界气流速控制。Turner模型和Coleman模型计算的气井携液临界气流速与液膜携带的临界气流速接近，李闽模型计算的气井携液临界气流速与单液滴携带的临界气流速接近。

气井携液临界气流速在什么条件下由液滴携带控制向液膜携带控制转化，与气流场中液滴的量及液滴间距有关。当气井井筒液流量增加后，液滴间距减小，液滴相互作用会削弱气流对液滴的有效作用力，为此液滴携带的气流速将增加。对于稠密多液滴相互作用机理及携带规律将是较大液量气井携液机理研究的重要方向。

3.2 模型准确性验证

Coleman等(1991)［3］文献试验数据共56组，油管内径均为62 mm，其中13组数据有明显的段塞特征，Coleman等判定为积液井，有9口井无产液量或产液量为0，有1口井油压数据为0，这23口井数据均未用于模型评价。考虑到气井液流量较大时，液滴数量多，液滴间距小，液滴相互作用明显，曳力系数将受影响，为了较真实反映单液滴模型准确性，选用了气井产液量小于1 m3/d的14口井的数据进行评价。模型计算值与测试值对比如图7所示。

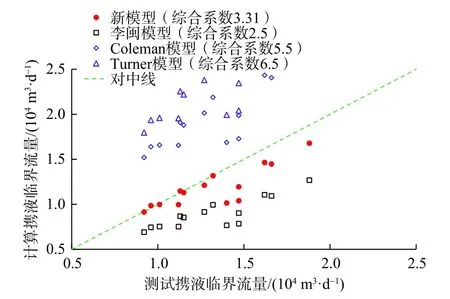
图7 现有单液滴模型携液临界气流量计算值与测试值对比Fig. 7 Comparison between the critical drop carrying gas flow rate calculated by existing single drop models and the measurement result

从图7可知，李闽椭球模型携液临界气流量较测试值偏小，Coleman圆球模型和Turner圆球模型计算值较测试值偏大很多。根据本研究的结果，将综合系数取为3.31计算的携液临界气流量与测试值较为接近。需特别说明的是，综合系数取3.31仅适合于低液量气井。对于高液量气井，或者液滴间距过小时，综合系数取值需要考虑液滴相互作用的影响，属于多液滴相互作用研究范畴，有待进一步研究。

4 结论

(1)建立了描述气流场中液滴动力学特征的数值模型，用于模拟气井高温高压高雷诺数条件下单液滴形状特征、变形规律、破碎条件和数值计算曳力系数。所建数值模型具有较高准确性，与实验结果吻合较好，曳力系数的平均绝对百分误差为9.98%，液滴椭球度的平均绝对百分误差为11.45%。

(2)在气流速作用下，液滴逐渐变形为椭球体；在韦伯数为1时，观测到液滴明显变形；随气流速或韦伯数增大，液滴变形后的椭球度增大；当韦伯数增加到12时，液滴的界面张力不能克服气流的气动力，液滴破裂为更小液滴；对于井筒流场中液滴稀疏的低液量气井，可将液滴破碎的临界韦伯数取为12，以此来确定流场中最大液滴的尺寸。

(3)通过对液滴进行受力分析得到液滴携带临界气流速综合系数，综合系数随韦伯数或液滴尺寸增加而增加，但增加幅度不大；液滴的韦伯数从1增加到12，或者液滴尺寸增加12倍时，综合系数从2.19增加到3.31，仅增加了51%，说明液滴尺寸不是影响液滴携带临界气流速的关键。

(4)本文采用数值模拟研究得到的综合系数3.31与李闽椭球模型中的系数2.5比较接近，但与Turner模型的系数6.5和Coleman模型的系数5.5相差较大。

(5) Turner模型和Coleman模型将液滴考虑为球状、临界韦伯数取为30、曳力系数取为0.44，与数值模拟研究的结果相差较大，说明这两种模型存在一定的理论缺陷，或者说在临界气流速预测时太过于保守。

(6)单液滴模型准确性评价表明，综合系数3.31适用于低液量(小于1 m3/d)气井，此时井筒液滴稀疏，液滴相互作用可忽略不计；对于大液量气井，流场中液滴数量大，液滴间距小，液滴相互作用会削弱气流对液滴的有效作用力，单液滴模型不适用。对于气井产液量多大，或者液滴间距多小时，液滴携带临界气流速计算需要考虑液滴相互作用的影响，属于多液滴相互作用研究范畴，有待进一步研究。