基于主成分分析和优化聚类算法的行驶工况研究

张林平， 李风军

(宁夏大学数学统计学院， 银川 750021)

随着经济的快速发展，汽车保有量不断增加,给城市交通带来了沉重的压力，并使得汽车排放成为中国主要城市空气污染的主要来源[1]. 行驶工况是量化汽车排放的一个重要概念，能充分反映汽车的实际行驶模式，从而获得可靠的汽车排放估计. 随着路网密度的改善，研究者越来越关注实际驾驶条件与各种车辆认证和监管机构所使用的标准行驶工况之间的差距.

汽车行驶工况作为一种被广泛采用的燃油经济性、排放和行驶里程评价基准，可以方便车辆设计和对新兴车辆技术性能评价，得到学者的广泛研究. 如：采用马尔科夫随机过程理论，构建了行驶工况图[2-4]；采用一种改进的马尔科夫蒙特卡罗方法构建了北京市的行驶工况图[5]；利用主成分分析和K均值聚类算法构建了行驶工况图[6-9]；提出了一种构造“行程段”的方法，构造了印度客车的行驶工况图[10]；利用多岛遗传算法(MIGA)与序列二次规划法(SQP)组合优化，对FCM聚类的初始聚类中心进行优化，从而构建了汽车行驶工况图[11]；利用粒子群优化算法优化了FCM的聚类中心，从而构建了行驶工况图[12]；利用主成分分析法和模糊C均值聚类算法，拟合了汽车行驶工况图[13]；利用自组织映射神经网络与粒子群聚类相结合的方法构建了汽车行驶工况图[14]. 上述研究方法虽然均构建了较理想的行驶工况图，但仍有需要改进的地方. 如：传统的主成分分析法可以达到降维的目的，但是没有完全体现出用数量较少的综合指标来代替原来多个指标的目的；对于模糊C均值聚类算法而言，在聚类过程中容易陷入局部最优，而遗传模拟退火算法可以防止其陷入局部最优.

鉴于此，本文改进了主成分分析，并将遗传模拟退火算法与模糊C均值聚类算法相结合成一种聚类算法(GSA-FCM)，从而构建更合理的汽车行驶工况图. 最后，将合成工况与实际工况的特征参数进行比对.

1 GSA-FCM算法

1.1 主成分分析法的改进

主成分分析法(Principal Component Analysis, 简称PCA)是一种数据降维的方法[15]. 其基本思想是用一组信息不重叠且数量较少的综合指标来代替原来多个具有一定相关性的指标，使其可以最大程度地反映原指标所代表的信息,即达到压缩数据的目的. 由于传统的PCA算法对原始数据进行了Z-Score标准化，没有完全展现各变量之间的差异信息，所以，本文对原始数据进行Min-Max标准化：设原始数据为X=(xij)n×p，则yij=(xij-minxj)/(maxxj-minxj) (i=1,2,…,n；j=1,2,…,p)，可得标准化后的矩阵Y=(yij)n×p；然后，对Y进行主成分分析.

1.2 遗传模拟退火算法优化模糊C均值聚类算法

模糊C均值聚类算法(Fuzzy C-means Algorithm，简称FCM或FCMA)是模糊聚类中应用最广泛的聚类方法之一[16]，即给定聚类数目，通过优化目标函数得到每个样本点属于每一类的隶属度[17]，从而达到聚类的目的. 设有n个样本xi(i=1,2,…,n)，可以分为k类，隶属矩阵U=(uij)n×k，uij是[0,1]中的随机数，并采取下列步骤来确定隶属矩阵和聚类中心：

(1)对隶属矩阵U初始化：

(2)计算聚类中心：

其中，ci为第i类聚类中心,m[1,∞]为加权指数;

(3)计算目标函数值：

其中

这里，ci为第i类聚类中心,dij=‖ci-xj‖为第i类聚类中心与数据样本之间的欧式距离;

(4)重新计算隶属矩阵U：

(5)如果目标函数值小于某个确定的阀值，则算法停止. 否则重复步骤(2)至步骤(4)，直到满足终止条件.

传统的遗传算法可以在全局求解最优解，但是迭代次数大、收敛速度慢. 通过引入模拟退火方法，可以提高进化过程中种群的多样性，避免算法陷入局部最优[18]，而模糊C均值聚类算法与K均值聚类算法在聚类过程中均易陷入局部最优，所以，本文采用遗传模拟退火算法(Genetic-Simulated Annealing，GSA)来优化模糊C均值聚类算法. 首先对种群中的个体进行选择、交叉、重组、变异，然后参与模拟退火，反复迭代，直到满足终止条件为止. 从而找到最优的初始聚类中心进行模糊C均值聚类，提高聚类效果. 具体流程如下：

Step 1: 设定各个参数值(例如初始温度、变异概率等)；

Step 2: 创建初始种群N(t)；

Step 3: 利用式(3)计算初始种群个体的目标函数值；

Step 4: 代数计数器初始化gen=0；

Step 5: 个体的选择select(N(t))；

Step 6: 个体的重组recombine(N(t))；

Step 7: 个体的变异mutation(N(t))；

Step 8: 个体的模拟退火；

Step 9: 若满足终止条件则输出最优个体，否则转到Step 4,直到满足终止条件；

Step 10: 得到最优的初始聚类中心；

Step 11: 用模糊C均值聚类算法进行聚类.

2 行驶工况的构建

汽车行驶工况的构建过程主要为运动学片段的划分、计算特征参数值、主成分分析、聚类、选择合适的片段合成工况. 本文以2019年全国研究生数学建模D题所提供的某市轻型汽车实际道路行驶所采集的493 467个数据为样本，构建该市汽车行驶工况图.

2.1 运动学片段及特征参数

运动学片段是指连续采集的数据从速度为零开始，到下一个速度为零为止. 特征参数是指能够反映车辆行驶特性变量的参数. 本文采用2019年全国研究生数学建模D题定义的4种工况[19]，具体如下：

怠速：v=0，且发动机一直以低速运转的行驶过程；

加速：a≥0.1m/s2的行驶过程；

减速：a≤-0.1m/s2的行驶过程；

匀速：|a|≤0.1m/s2非怠速的行驶过程.

特征参数的选取见表1.

表1 所选特征参数Table 1 The seleced characteristic parameters

2.2 特征参数的计算

本文所用特征参数的具体计算公式如下:

其中，ai,i+1表示第i时刻到第i+1时刻的加速度，vi表示第i时刻的速度，ti表示第i时刻，k表示GPS所测车速的总个数.

利用Matlab 2017b编程软件可得2 348个片段的特征参数值，部分片段的特征参数值见表2.

2.3 主成分分析数据

利用传统的PCA算法[20]和本文改进的PCA算法，分别对所得的2 348个片段进行降维处理，可得14个主成分的贡献率. 由结果(表3)可知：(1)改进后的PCA算法所得的第一主成分的贡献率比传统的PCA算法的高出14%. (2)改进后的PCA算法可以达到用数量较少的指标来代替原来多个指标的目的：传统的PCA算法所得的前5个主成分的累积贡献率达到了87.37%，而改进的PCA算法所得的前3个主成分的累积贡献率就已经达到了89.51%.

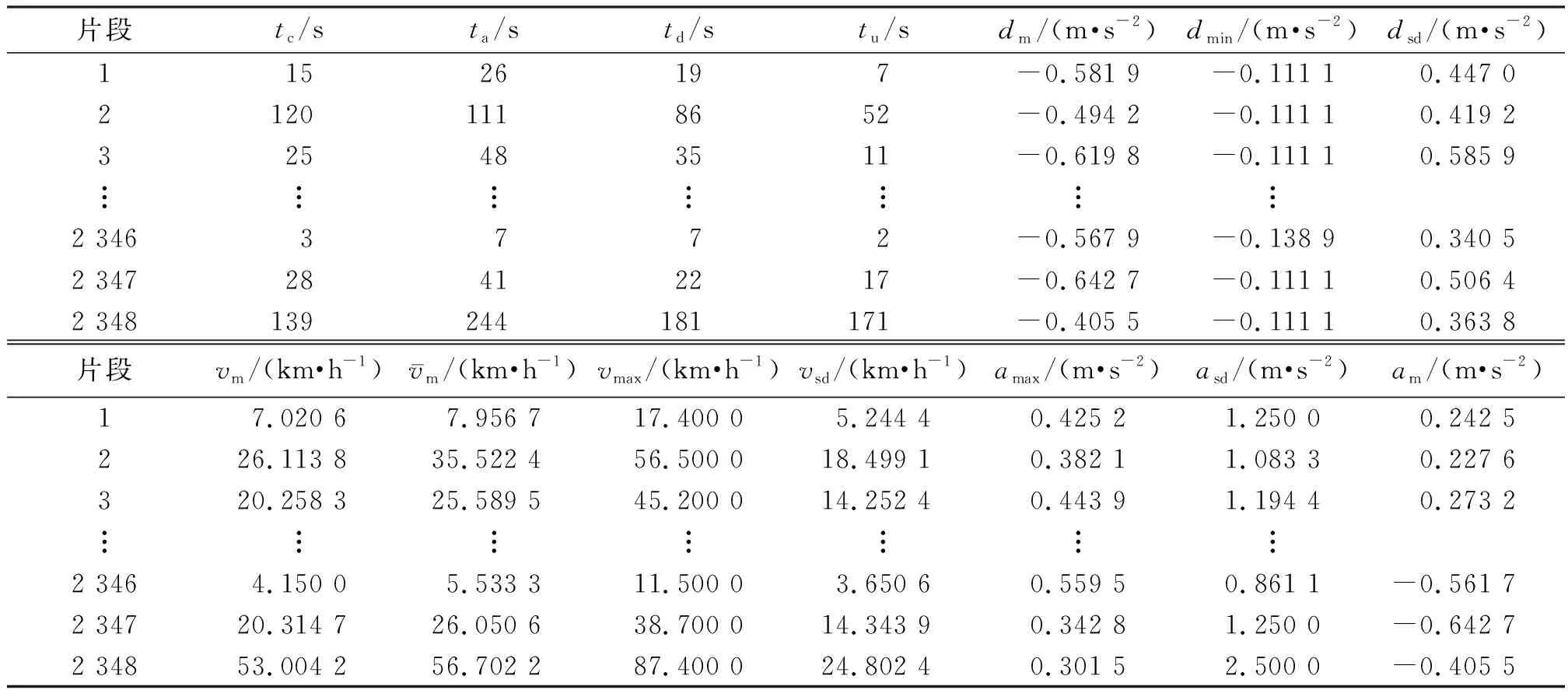
表2 部分片段的特征参数值Table 2 The characteristic parameter values of some fragments

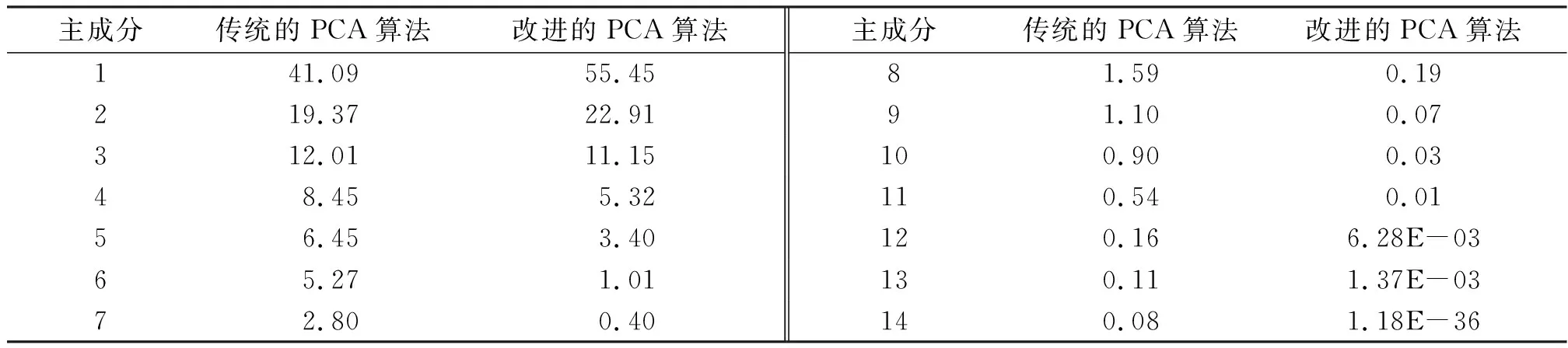
表3 各主成分贡献率Table 3 The contribution rates of each principal component %

利用主成分分析可以得到2 348个运动学片段的前3个主成分的得分，部分运动学片段的前3个主成分得分见表4.

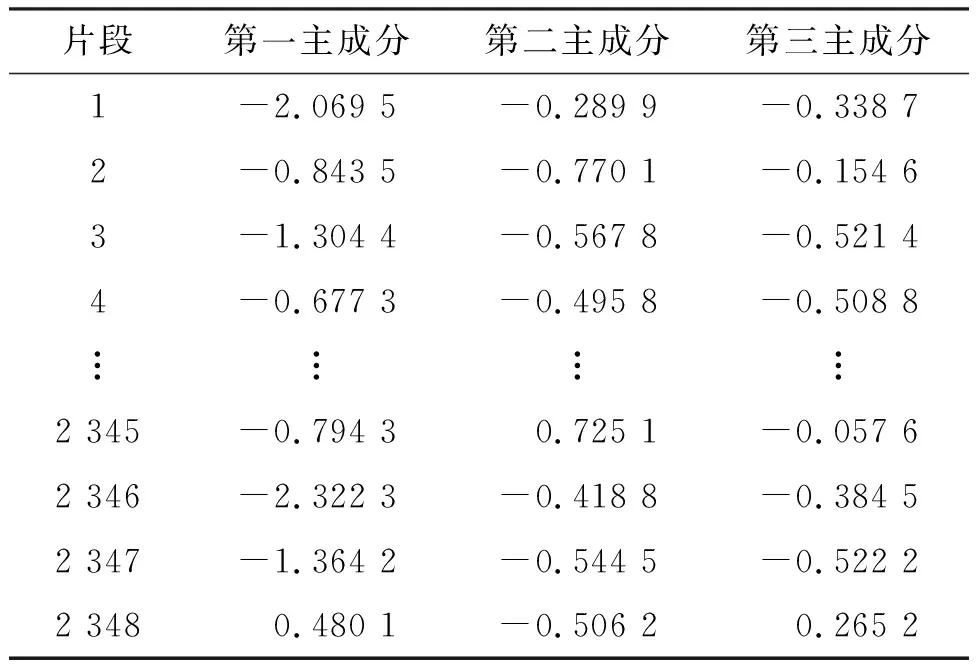
表4 部分运动学片段主成分得分Table 4 The principal component scores of kinematics fragments

2.4 聚类结果分析

使用传统的K均值聚类算法[21]，对2 348片段的前3个主成分得分进行聚类. 由聚类结果(图1)可知：2 348个运动学片段被分为3类，分别为579个第1类的运动学片段、843个第2类的运动学片段、926个第3类的运动学片段，聚类的整体效果较好，但是比较离散. 聚类中心具体值见表5.

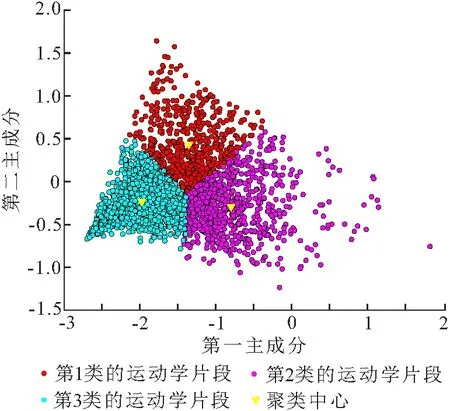
图1 K均值聚类结果

表5 K均值聚类中心Table 5 The K-means clustering center

利用GSA-FCM聚类算法对2 348片段的前3个主成分得分进行聚类，由聚类结果(图2)可知：2 348个运动学片段被划分为3类，虽然有部分点比较分散，但是相比K均值聚类算法，整体聚类效果更加明显，说明使用GSA优化FCM聚类算法的初始聚类中心，可以防止FCM聚类陷入局部最优，达到更好的聚类效果. 各类的聚类中心如表6所示.

图2 GSA-FCM聚类结果

表6 GSA-FCM的聚类中心Table 6 The GSA-FCM clustering center

2.5 行驶工况的合成

在行驶工况的合成中，最重要的就是运动学片段的选择，合适的运动学片段可以呈现聚类所得的每一类运动学片段所代表的行驶状况. 所以，本文采用如下步骤选取运动学片段：

(1)对每类所属运动学片段的特征参数进行Min-Max标准化处理，并求出每类运动学片段的特征参数之和，记为A；

(2)计算每类所属运动学片段每个特征参数的平均值，并对其进行Min-Max标准化后求和，记为B；

(3)计算A与B的绝对误差，按升序排列；

(4)计算每类片段所用的时间在所有片段所用总时间中的比例，从而确定每一类别在合成行驶工况里所占的时间，计算公式如下：

(1)

其中，ti表示第i(i=1,2,3)类运动学片段在最终构建工况曲线中所占的时间，M表示最终构建工况所用的时间，ti,m表示第i(i=1,2,3)类运动学片段中第m个运动学片段所用的时间，ni表示第i(i=1,2,3)类运动学片段总数；

(5)根据时间比例从每类运动学片段中选择绝对误差最小的片段合成最终工况图.

根据上述步骤，合成工况所用的时间一般为1 200～1 300 s. 由式(1)可得选取3类运动学片段所用时间分别为642.105 0～695.613 7 s、332.686 3～360.410 1 s、225.208 7～243.976 1 s.

由2种聚类算法所合成的行驶工况图(图3、图4)可知：利用传统的K均值聚类算法所得的行驶工况图中怠速状态较多；利用GSA-FCM聚类算法所得的行驶工况图显示汽车的行驶速度大部分为0～20 km/h，处于低速状态，高速行驶情况较少，与实际情况相符.

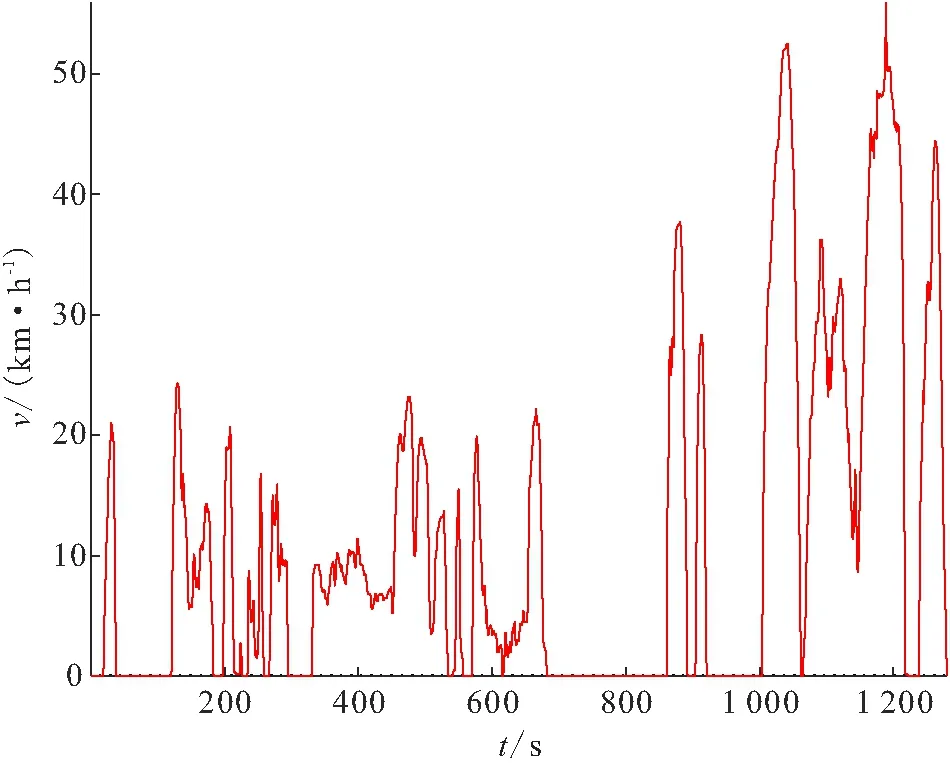
图3 K均值聚类合成工况图

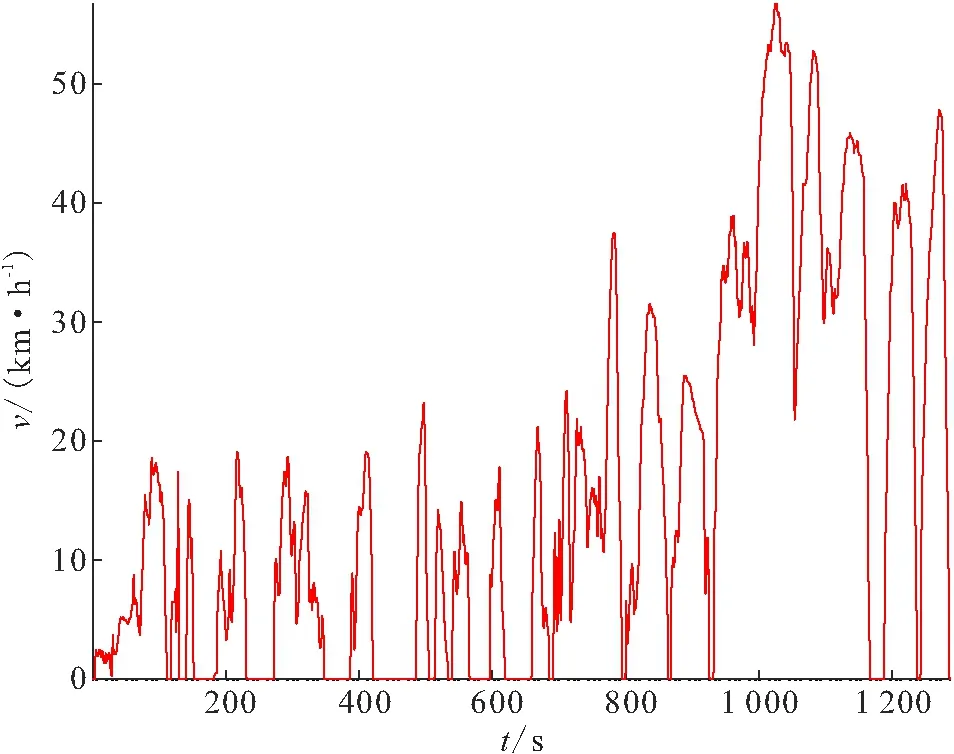
图4 GSA-FCM最终拟合工况图

3 合成工况的精度分析与比对

在合成工况之后，需要检验该工况是否具有代表性. 本文基于特征参数的误差进行比对，即选择平均速度、平均加速度和平均减速度等9个具有代表性的特征参数为评价指标，分别计算原始数据合成的实际工况与GSA-FCM聚类算法、传统的K均值聚类算法所合成工况的特征参数值并进行误差分析. 由结果(表7)可知：GSA-FCM聚类算法有1个指标的相对误差较大，其他8个指标的相对误差均在10%以下，所有特征值的平均相对误差仅为 6.46%；传统的K均值聚类算法有6个指标的相对误差大于10%，平均相对误差为16.17%. 由此可知：利用GSA-FCM聚类算法所合成的行驶工况图的误差小、精度高，可以反映原始数据所蕴含的工况信息.

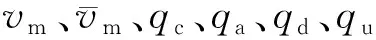
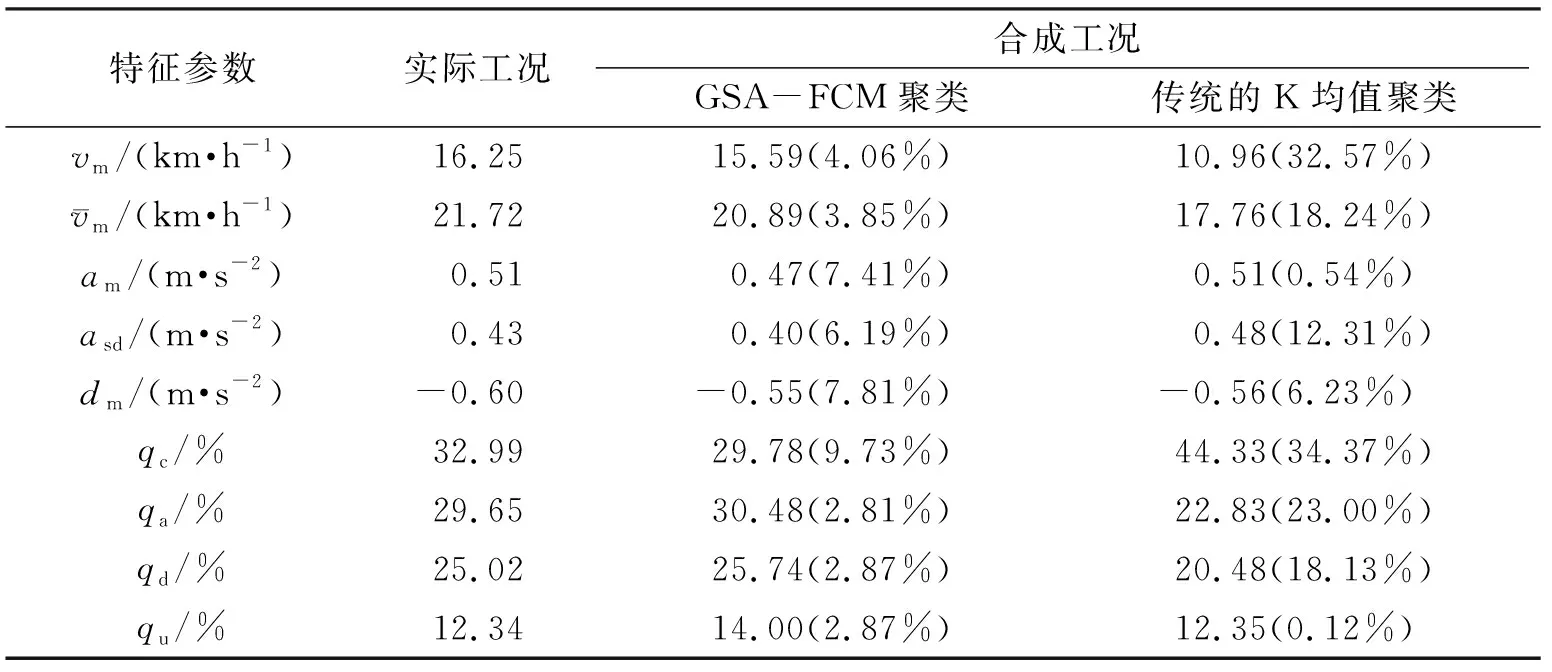
表7 基于特征参数的实际工况与合成工况分析Table 7 The analysis of actual working condition and synthetic working condition based on characteristic parameters

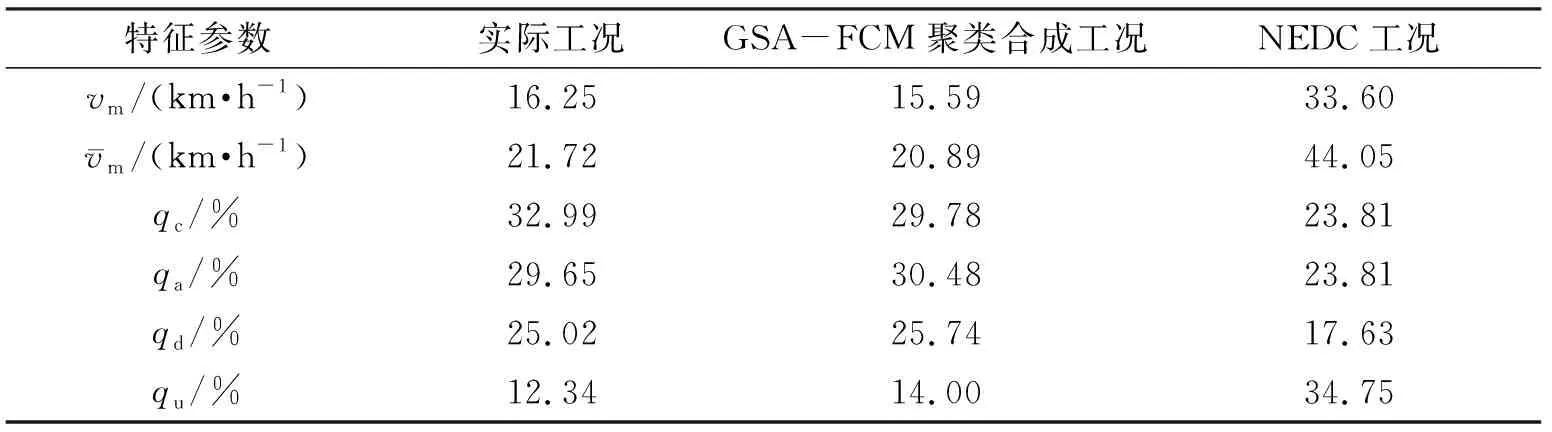
表8 合成工况与NEDC标准测试工况对比Table 8 The comparison of synthetic conditions and NEDC standard test conditions

4 总结

本文提出一种改进的主成分分析和利用遗传模拟退火算法优化后的模糊C均值聚类算法相结合的聚类算法(GSA-FCM)，以构建汽车行驶工况图. 并将该聚类算法和传统的K均值聚类算法所合成的行驶工况的特征参数值与实际工况的特征参数值进行比较，所得平均相对误差分别为6.46%、16.17%，充分说明使用GSA-FCM聚类算法所合成的行驶工况图的误差小、精度高. 由GSA-FCM聚类算法合成的工况、NEDC标准测试工况与实际工况的对比结果可知：实际工况与NEDC工况存在显著的差异,与GSA-FCM聚类合成工况差异较小,说明NEDC工况图不能代表该市汽车的行驶状况,而GSA-FCM聚类合成工况与该市汽车的行驶状况更相符.