随机环辛烷链的三类 Kirchhoff指数

刘合超， 吴让威， 尤利华

(华南师范大学数学科学学院， 广州 510631)

拓扑指数是一类刻画分子结构的数值不变量. 在理论化学中,拓扑指数被用于预测化合物的物理化学性质、药理活性和生理活性等. 常用的与距离有关的拓扑指数主要有 Wiener 指数[1-2]、 Harary 指数[3]和Kirchhoff 指数[4].

环辛烷及其衍生物是有机化学中重要的环烷烃,可用于药物合成、有机合成等. 而研究一些特殊化学链的拓扑指数及其在化学中的应用也成为化学图论的热点问题[5-13]. 如：WU等[5]计算了聚苯链、聚苯蜘蛛链的hyper-Wiener指数,得到上、下界;YANG和ZHANG[6]给出了随机聚苯链的Wiener指数的期望值;WEI等[12]给出了随机环辛烷链的 Wiener指数的期望值;ZHANG等[13]确定了随机聚苯链的Schultz指数、Gutman指数、度积Kirchhoff指数、度和Kirchhoff指数的期望值.

关于Kirchhoff指数的研究已经有比较多的成果. 如：YANG和JIANG[14]给出了单圈图的Kirchhoff指数的极大、极小值;GUO等[15]确定了全负荷单圈图的Kirchhoff指数的极大、极小值;FENG等[16]刻画了具有极大、极小度Kirchhoff指数的全负荷单圈图;FEI和TU[17]刻画了具有最大、第二大度Kirchhoff指数的双圈图. 关于更多介绍Kirchhoff指数的性质及其应用的文献可参考文献[18-21]. 在文献[12-13]的启发下,本文首先确定了随机环辛烷链的3类Kirchhoff指数(Kirchhoff指数、度积Kirchhoff指数、度和Kirchhoff指数)的期望表达式,再由该式得到了具有n个八边形的环辛烷链的3类Kirchhoff指数的极大值与极小值,并刻画了相应的极图.

1 预备知识

在 Wiener 指数的定义中用电阻距离替代距离,则可得到 Kirchhoff 指数[4]：

度积Kirchhoff指数Kf*(G)[23]与度和Kirchhoff指数Kf+(G)[24]是2类加权版的Kirchhoff指数,分别定义为:

图1为一条具有n个正八边形的环辛烷链COCn,可以看成是将环辛烷链COCn-1通过一条割边连接一个新的终端正八边形On所构成的.

图1 n个正八边形的环辛烷链COCn

设COCn=O1O2…On为具有n(n≥2)个正八边形的环辛烷链,其中Ot(t=2,3,…,n)为图COCn中通过割边ut-1vt与Ot-1相连的第t个正八边形. 在Ot中,与点vt距离为1、2、3、4的点分别记为ot、mt、wt、lt. 例如:图1中vn=z1;on=z2,z8;mn=z3,z7;wn=z4,z6;ln=z5.

在具有n个正八边形的环辛烷链COCn中,有一些特殊类的COCn. 例如:对任意的2≤t≤n-1,若均有ut=ot,则将该环辛烷链COCn记为COn;若ut=mt,则将其记为CMn;如ut=wt,则将其记为CWn;若ut=lt,则将其记为CLn.

图2 环辛烷链的4种连接方式

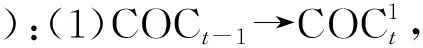
特别地,COC(n;1,0,0)、COC(n;0,1,0)、COC(n;0,0,1)、COC(n;0,0,0)分别为链COn、CMn、CWn、CLn.

2 随机环辛烷链的Kirchhoff指数

引理1设COCn为具有n(n≥1)个正八边形的环辛烷链,则

Kf(COCn)=Kf(COCn-1)+8r(un-1|COCn-1)+

148(n-1)+42.

(1)

对于任意顶点vV(COCn-1),由图1知r(zi,v)=r(zi,un-1)+r(un-1,v),且

(2)

对于zkV(On)(1≤k≤8),有

从而

(3)

进而

8r(un-1|COCn-1)+148(n-1)+42.

故式(1)成立. 证毕.

记Un=E[r(un|COCn)],下面给出Un的表达式.

引理2设COC(n;p1,p2,p3)为具有n(n≥1)个正八边形的随机环辛烷链,则

(4)

证明分以下4种情况来计算Un.

由情形1至情形4及式(3),可知

Un=r(z2|COCn)p1+r(z3|COCn)p2+r(z4|COCn)p3+

r(z5|COCn)(1-p1-p2-p3)=

(1-p1-p2-p3)[r(un-1|COC(n-1;p1,p2,p3))+

而E[Un]=Un,则

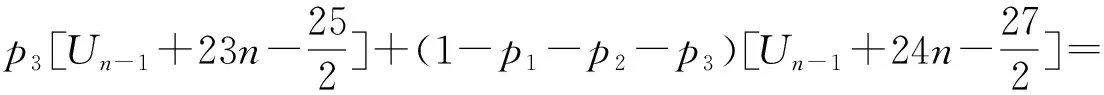
(5)

由引理1和引理2,易得随机环辛烷链的Kirchhoff指数的期望值.

定理1设COC(n;p1,p2,p3)为具有n(n≥1)个正八边形的随机环辛烷链,则

E[Kf(COC(n;p1,p2,p3))]=

(6)

证明对式(1)两边取期望,由式(4),有

E[Kf(COC(n;p1,p2,p3))]=

E[Kf(COC(n-1;p1,p2,p3))]+

8E[r(un-1|COC(n-1;p1,p2,p3))]+

148(n-1)+42=E[Kf(COC(n-1;p1,p2,p3))]+

8Un-1+148n-106.

从而

E[Kf(COC(n+1;p1,p2,p3))]=

E[Kf(COC(n;p1,p2,p3))]+(96-36p1-16p2-4p3)n2+

(136+36p1+16p2+4p3)n+42.

(7)

将初始值E[Kf(COC(1;p1,p2,p3))]=42代入式(7),递归可得式(6)成立. 证毕.

由于COC(n;1,0,0)、COC(n;0,1,0)、COC(n;0,0,1)、COC(n;0,0,0)分别为链COn、CMn、CWn、CLn. 将(p1,p2,p3)=(1,0,0)、(p1,p2,p3)=(0,1,0)、(p1,p2,p3)=(0,0,1)、(p1,p2,p3)=(0,0,0)分别代入定理1的期望表达式,易得下面的推论.

推论14种特殊环辛烷链COn、CMn、CWn、CLn的Kirchhoff指数为

Kf(COn)=20n3+56n2-34n,

Kf(CLn)=32n3+20n2-10n.

下面给出环辛烷链的Kirchhoff指数达到上、下界的极图刻画.

定理2在所有具有n(n≥3)个正八边形的环辛烷链中,CLn是具有最大Kirchhoff指数的惟一的环辛烷链,CMn是具有最小Kirchhoff指数的惟一的环辛烷链.

证明设COC(n;p1,p2,p3)是具有n(n≥3)个正八边形的随机环辛烷链. 由定理1,有

f(p1,p2,p3)=E[Kf(COC(n;p1,p2,p3))]=

当n≥3 时,有

而0≤p1,p2,p3≤1,0≤p1+p2+p3≤1,所以f(p1,p2,p3)≤32n3+20n2-10n,等号成立当且仅当p1=p2=p3=0,即CLn是具有最大Kirchhoff指数的惟一的环辛烷链.

另一方面,有

f(p1,p2,p3)=(-12n3+36n2-24n)(p1+p2)+

显见

(8)

3 随机环辛烷链的度积 Kirchhoff 指数

在有n(n≥2)个正八边形的环辛烷链COCn中:第1个和第n个正八边形中恰有1个3度点,其余7个点都是2度点;在其余的n-2个正八边形中,恰有2个3度点,其余都是2度点;在On中,d(z1)=3,d(zi)=2(2≤i≤8). 所以

且在On中,

(9)

下面求Kf*(COC(n;p1,p2,p3))的期望值. 记V=V(COCn),V1=V(COCn-1),V2=V(COCn-1){un-1}.

定理3设COC(n;p1,p2,p3)为具有n(n≥1)个正八边形的随机环辛烷链,则

E[Kf*(COC(n;p1,p2,p3))]=

(10)

证明令Kf*(COCn)=A1+B1+C1,其中

由式(2)、(9)及对称性,类似地,有

38(18n-19),

因此,

684n-533.

(11)

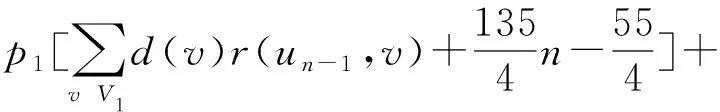
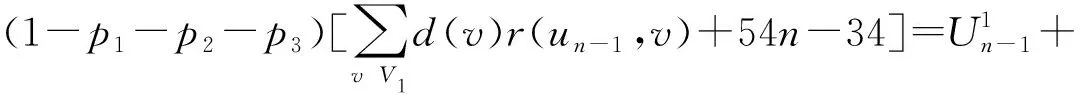
(12)

再由式(11)、(12)可得

E[Kf*(COC(n+1;p1,p2,p3))]=

导入初始值E[Kf*(COC(1;p1,p2,p3))]=168,递归可得式(10)成立. 证毕.

将(p1,p2,p3)=(1,0,0),(0,1,0),(0,0,1),(0,0,0)代入式(10),易得下面的推论.

推论24种特殊环辛烷链COn,CMn,CWn,CLn的度积Kirchhoff指数为

Kf*(CMn)=135n3+117n2-83n-1,

Kf*(CLn)=162n3+36n2-29n-1.

下面给出环辛烷链的度积Kirchhoff指数达到上、下界的极图刻画.

定理4在所有具有n(n≥3)个正八边形的环辛烷链中,CLn是具有最大度积Kirchhoff指数的惟一的环辛烷链,CMn是具有最小度积Kirchhoff指数的惟一的环辛烷链.

证明设COC(n;p1,p2,p3)为具有n(n≥3)个正八边形的随机环辛烷链. 由定理3,有

f1(p1,p2,p3)=E[Kf*(COC(n;p1,p2,p3))]=

当n≥3时,有

而0≤p1,p2,p3≤1,0≤p1+p2+p3≤1,所以f1(p1,p2,p3)≤162n3+36n2-29n-1,等号成立当且仅当p1=p2=p3=0,即CLn是具有最大度积Kirchhoff指数的惟一的环辛烷链.

另一方面,有

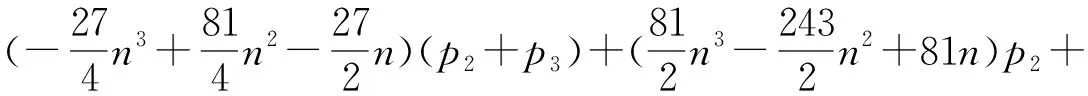
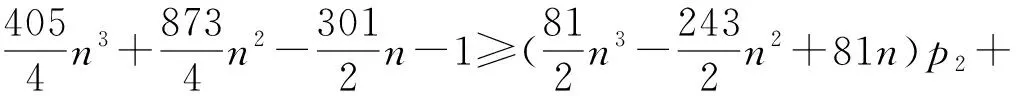
显见

(13)

的等号成立当且仅当p1+p2=1,p2+p3=1且0≤p1+p2+p3≤1,即(p1,p2,p3)=(0,1,0). 将p2=1代入式(13)可得f1(p1,p2,p3)≥135n3+117n2-83n-1,等号成立当且仅当(p1,p2,p3)=(0,1,0),即CMn是具有最小度积Kirchhoff指数的惟一的环辛烷链. 证毕.

4 随机环辛烷链的度和Kirchhoff指数

本节求Kf+(COC(n;p1,p2,p3))的期望值. 仍记V=V(COCn),V1=V(COCn-1),V2=V(COCn-1){un-1}.

定理5设COC(n;p1,p2,p3)为具有n(n≥1)个正八边形的随机环辛烷链,则

E[Kf+(COC(n;p1,p2,p3))]=6(24-9p1-4p2-p3)n3+

(14)

由式(2)、(9),类似地,有

Kf+(COCn-1)+r(un-1|COCn-1),

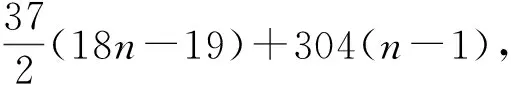
因此,

Kf+(COCn)=Kf+(COCn-1)+18r(un-1|COCn-1)+

(15)

r(z5|COCn)(1-p1-p2-p3)=

(16)

由式(15)、(16),可得

E[Kf+(COC(n+1;p1,p2,p3))]=

E[Kf+(COC(n;p1,p2,p3))]+18(24-9p1-4p2-p3)n2+

代入初始值E[Kf+(COC(1;p1,p2,p3))]=168,递归可得式(14)成立. 证毕.

将(p1,p2,p3)=(1,0,0),(0,1,0),(0,0,1),(0,0,0)分别代入式(14),易得如下推论.

推论34种特殊环辛烷链COn,CMn,CWn,CLn的度和Kirchhoff指数为

Kf+(COn)=90n3+223n2-145n,

Kf+(CMn)=120n3+133n2-85n,

Kf+(CWn)=138n3+79n2-49n,

Kf+(CLn)=144n3+61n2-37n.

下面给出环辛烷链的度和 Kirchhoff 指数达到上、下界的极图刻画.

定理6在所有具有n(n≥3)个正八边形的环辛烷链中,CLn是具有最大度和 Kirchhoff 指数的惟一的环辛烷链,CMn是具有最小度和 Kirchhoff 指数的惟一的环辛烷链.

证明设COC(n;p1,p2,p3)为具有n(n≥3)个正八边形的随机环辛烷链. 由定理5,有

f2(p1,p2,p3)=E[Kf+(COC(n;p1,p2,p3))]=

(-54n3+162n2-108n)p1+(-24n3+72n2-48n)p2+

(-6n3+18n2-12n)p3+144n3+61n2-37n.

当n≥3 时,有

而0≤p1,p2,p3≤1,0≤p1+p2+p3≤1,所以f2(p1,p2,p3)≤144n3+61n2-37n,等号成立当且仅当p1=p2=p3=0,即CLn是具有最大度和Kirchhoff指数的惟一的环辛烷链.

另一方面,有

f2(p1,p2,p3)=(-54n3+162n2-108n)(p1+p2)+

(30n3-90n2+60n)p2+(-6n3+18n2-12n)p3+

162n3+144n3+61n2-37n≥(30n3-90n2+60n)p2+

(-6n3+18n2-12n)p3+90n3+223n2-145n=

(-6n3+18n2-12n)(p2+p3)+(36n3-108n2+72n)p2+

90n3+223n2-145n≥(36n3-108n2+72n)p2+84n3+

241n2-157n.

显见

f2(p1,p2,p3)≥(36n3-108n2+72n)p2+

84n3+241n2-157n

(17)

的等号成立当且仅当p1+p2=1,p2+p3=1且0≤p1+p2+p3≤1,即(p1,p2,p3)=(0,1,0). 将p2=1代入式(17)，可得f2(p1,p2,p3)≥120n3+133n2-85n,等号成立当且仅当(p1,p2,p3)=(0,1,0),即CMn是具有最小度和Kirchhoff指数的惟一的环辛烷链. 证毕.

5 随机环辛烷链的3类Kirchhoff指数的平均值

定理7环辛烷链集n的3类 Kirchhoff 指数的平均值分别为

我们发现

Kf*(CWn)+Kf*(CLn)),

Kf+(CLn)).

这意味着可以用这4条特殊的链COn、CMn、CWn、CLn的Kirchhoff指数(度积Kirchhoff指数、度和Kirchhoff指数)的平均值来表示n的Kirchhoff指数(度积Kirchhoff指数、度和Kirchhoff指数)整体的平均值.