强一致收敛下弱几乎周期点和周期序列跟踪性的研究

冀占江， 张更容

(1. 梧州学院大数据与软件工程学院∥广西高校图像处理与智能信息系统重点实验室∥广西高校行业软件技术重点实验室， 梧州 543002; 2. 湖南第一师范学院数学与计算科学学院， 长沙 410205)

周期序列跟踪性和弱几乎周期点是动力系统中非常重要的概念，与系统的混沌有着密切的联系，在计算机领域也有着重要的应用.

本文在文献[5]的基础上得到弱几乎周期点集的拓扑结构，并研究了强一致收敛下的周期序列跟踪性，以期促进强一致收敛下弱几乎周期点和周期序列跟踪性理论的发展.

1 基本概念

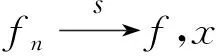
定义1[1]设(X,d)是度量空间，对∀n+，fn:X→X连续，f:X→X连续. 称序列映射{fn}在X上强一致收敛于f，如果∀ε>0，∃n0+，当n>n0时，∀xX，∀m≥0，有记作

定义2[5]设(X,d)是度量空间，f:X→X连续，xX． 若对∀ε>0，∃N>0，对∀n≥0，有#({r:fr(x)B(x,ε),0≤r

定义3[14]设(X,d)是度量空间，f:X→X连续． 若对∀ε>0，∃δ>0,使得当{xi}i≥0是X中f的δ-周期伪轨时，∃yP(f)，∃{ni|ni+1>ni,ni踪则称f具有周期序列跟踪性．

定义4[14]设(X,d)是度量空间，f:X→X连续． 若对∀ε>0，使得当{xi}i≥0是f的ε-周期伪轨时，∃yP(f)，∃{ni|ni+1>ni,ni踪则称f具有fine周期序列跟踪性．

2 主要结论

证明因为f是等度连续的，所以∀ε>0，∃0<δ<ε/3，当d(z1,z2)<δ时，∀l≥0，有

(1)

(2)

结合引理1，可知xm是f的弱几乎周期点，因此,对ε/3>0，∃q>0，∀n≥0，有

#({r:fr(xm)B(xm,ε/3),0≤r

令An={r:fr(xm)B(xm,ε/3),0≤r

(3)

由式(2)、(3)，可得

d(fr(x),x)

则rBn，An⊂Bn，故#Bn>#An≥n. 因此，点x是极限映射f的弱几乎周期点.

证明因为f是等度连续的，故∀ε>0，∃0<δ<ε/4，当d(z1,z2)<δ时，∀l≥0，有

(4)

(5)

设zlimsupW(fn)，则∃m>N1(m+)，使得

W(fm)∩B(z,δ)≠∅.

取yW(fm)∩B(z,δ). 由于yW(fm)，故对ε/4>0，∃q>0，对∀n，有

(6)

则由yB(z,δ)和式(4)，有

(7)

再由式(5)～(7)，可得

则rBn，An⊂Bn，故#Bn>#An≥n，因此，zW(f)，从而可得limsupW(fn)⊂W(f).

注1在强一致收敛下，即使满足定理2的条件，也存在limsupW(fn)≠W(f)的情况.

例1设I=[0,1]，对n+，定义fn:X→X

定义f:X→X

f(x)=x(x[0,1])，

则limsupW(fn)≠W(f).

(8)

若x当k≥1时，有

若x当k≥2时，有

若x当k≥3时，有

依此类推，若x则∃m=m(n,x)+，当k≥m时，有

故式(8)成立. 设x(0,1]. 下面证明xW(fn). 假设xW(fn)，则∀ε>0，∃m0>m,使得B(x,ε). 由式(8)可得故0B(x,ε)，这与ε的任意性矛盾，故xW(fn). 又0W(fn)，则W(fn)={0}. 故limsupW(fn)={0}，因此limsupW(fn)≠W(f).

d(f(xi),xi+1)<δ.

(9)

(10)

取m>N1并固定m，根据式(10)，当i≥0时，有

d(fm(xi),f(xi))<δ.

(11)

再由式(9)、(11)，可得

由于映射fm具有fine周期序列跟踪性，则∃xP(fm)，∃{ni|ni+1>ni,ni当i≥0时，有

(12)

再由式(10)可得：当i≥0时，有

(13)

结合式(12)、(13)可得：当i≥0时，有

下面证明xP(f). 因为xP(fm)，所以，∃k>0，使得根据式(10)可得

故

由于ε是任意小的，则fk(x)=x，故xP(f)，从而可得f具有周期序列跟踪性.

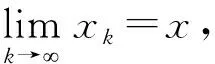
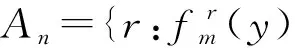
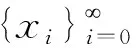
3 总结