带变号格林函数的三阶三点边值问题的正解的存在性

雷策宇， 韩晓玲

(西北师范大学数学与统计学院, 兰州 730070)

三阶常微分方程边值问题由于在工程、物理和流体力学等领域的显著应用而受到广泛关注. 学者们运用单调迭代法、上下解方法、Guo-Krasnosel’skii不动点定理和 Leray-Schauder 非线性抉择等,研究了三阶三点边值问题在格林函数非负的情况下的单个或多个正解的存在性[1-7]. 近年来,学者们在格林函数变号的情况下也得到了很多结果[8-17]. 如:LI等[9]使用Guo-Krasnosel’skii不动点定理讨论了变号格林函数的三阶三点边值问题

正解的存在性,其中,α[0,2),η

GAO和SUN[10]运用Avery-Henderson不动点定理,在格林函数变号时讨论了问题

正解的存在性,其中,α[0,2),η

ZHAO和LI[11]运用迭代法讨论了变号格林函数的三阶三点边值问题

正解的存在性, 其中,α[0,2),η[2/3,1).

受文献[11]的启发,本文将运用迭代法,研究如下具有变号格林函数的三阶三点边值问题

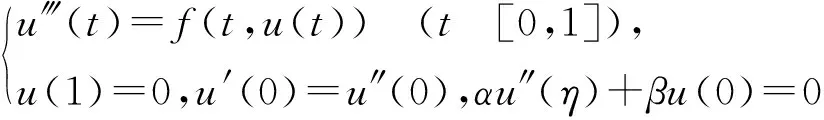
(1)

正解的存在性,其中,α[2/3,1). 在本文中,总是假设fC([0,1]×[0,∞),[0,∞)),且f满足下列2个条件:

(H1) 对于每一个u[0,+∞),映射tf(t,u)是递减的；

(H2) 对于每一个t[0,1],映射uf(t,u)是递增的.

1 预备知识

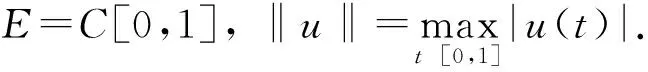
引理1 对任意的yC[0,1],边值问题

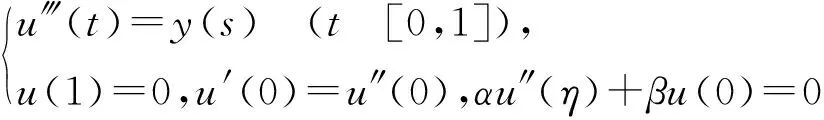
(2)

有唯一解

其中:

G(t,s)=g1(t,s)+g2(t,s)+g3(η,t,s);

证明对u‴(t)=y(t)在[0,t]上两边积分,得

由边界条件可得

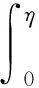
从而有

故边值问题(2)的解为

证毕.

引理2G(t,s)具有如下性质:

(1)当0≤s≤η时,G(t,s)≥0;

(2)当0≤η≤s时,G(t,s)≤0.

证明当0≤s≤η时,有

G(t,s)=

分以下2种情况讨论:

(1)当 0≤t≤s≤1 时,有

(2)当 0≤s≤t≤1 时,有

综上可知,G(t,s)关于变量t单调递减. 从而有

min{G(t,s),t[0,1]}=G(1,s)=0,

max{G(t,s),t

故当0≤s≤η时,G(t,s)≥0.

同理可证得:当0≤η≤s时,G(t,s)关于变量t单调递增. 则有

max{G(t,s),t[0,1]}=G(1,s)=0,

min{G(t,s),t

从而G(t,s)≤0. 证毕.

设M=max{|G(t,s)||t,s[0,1]},则

设K={yE|y(t)在[0,1]上非负且递减},则K是E中的一个锥,且在E中定义一个序关系“≤”,u≤ν当且仅当ν-uK.

定义算子T:K→E

显然,若u是T中的不动点,则u是边值问题(1)的递减非负解.

引理3算子T:K→K是全连续的.

证明设uK,当t[0,η]时,有

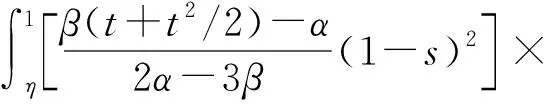
f(s,u(s))ds.

由条件(H1)、(H2),可得

(Tu)′(t)=

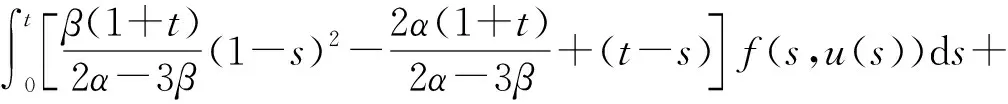
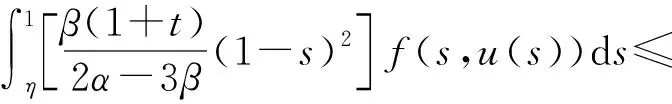
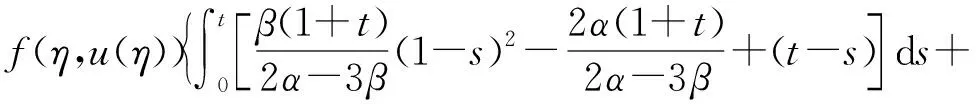
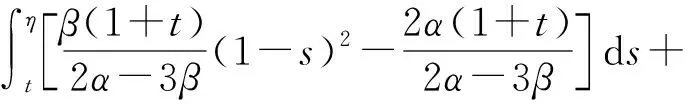
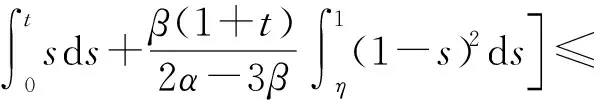
当t[η,1]时,有

f(s,u(s))ds,

则

(Tu)′(t)=

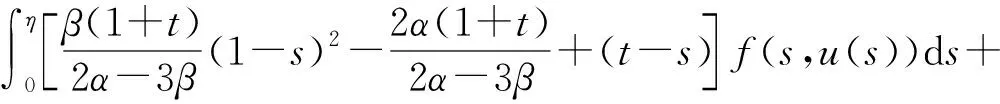
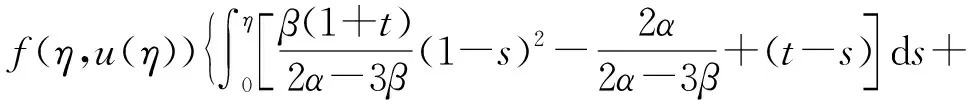
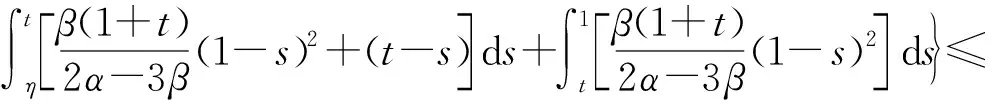
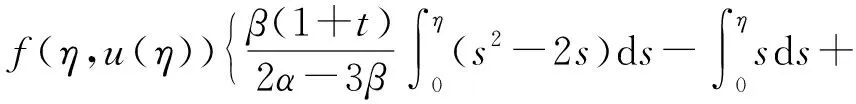
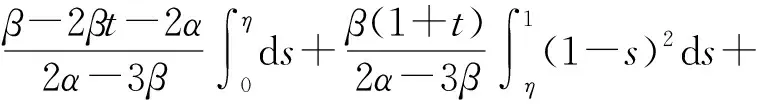
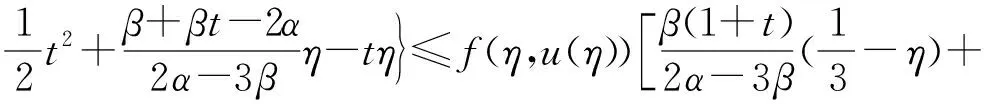
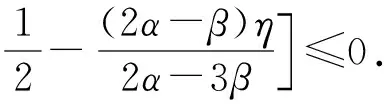
综上可知,(Tu)(t)在[0,1]上单调递减. 又由于(Tu)(1)=0,故(Tu)(t)在[0,1]上非负,从而TuK. 假设D⊂K是有界集,则存在一个常数C1>0,使得‖u‖≤C1(uD). 下证T(D)是相对紧的.

设C2=sup{f(t,u)|(t,u)[0,1]×[0,C1]}. 对∀yT(D),∃uD,使得y=Tu,则对∀t[0,1],有

MC2,

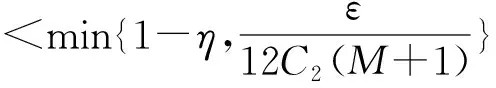
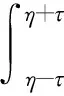
(3)

因为G(t,s)在[0,1]×[0,η-τ]和[0,1]×[η+τ,1]上一致连续,故∃δ>0,使得对∀t1,t2[0,1],当|t1-t2|<δ时,有

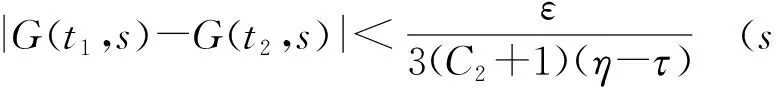
(4)

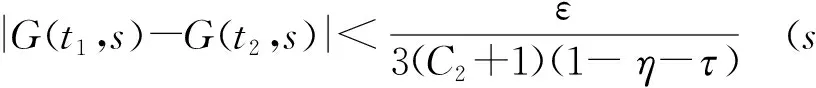
(5)

由式(3)～(5)及对∀yT(D),∀t1,t2[0,1]和|t1-t2|<δ,有

|y(t1)-y(t2)|=|T(t1)-T(t1)|=

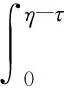
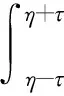
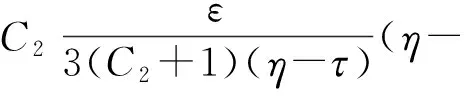
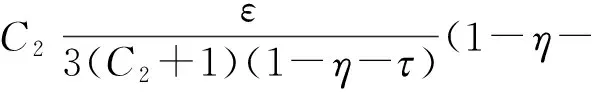
故T(D)是等度连续的,从而由Arzela-Ascoli定理[18]知T(D)是相对紧的. 因此,T是紧算子.

最后,证明T是连续的. 设un(n=1,2,…),u0K,‖un-u0‖→ 0(n→ 0),则∃C3>0,使得对∀n,‖u‖≤C3.

设C4=sup{f(t,u)|(t,u)[0,1]×[0,C3]}. 对∀n,t[0,1],∀s[0,1],有

G(t,s)f(s,un(s))≤MC4.

由Lebesgue控制收敛定理[19],对∀t[0,1],有

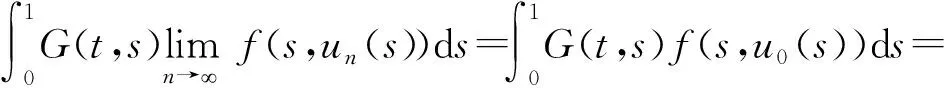
(Tu0)(t),

这表明T是连续的. 因此,T:K→K是全连续的. 证毕.

2 主要结果及证明

定理1假设条件(H1)、(H2)成立,且对于f(t,0)≠0,∀t[0,1],存在2个正实数a和b,满足以下条件：

(H4)b(u2-u1)≤f(t,u2)-f(t,u1)≤2b(u2-u1) (0≤t≤1,0≤u1≤u2≤a).

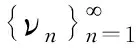
证明设Ka={uK|||u||≤a}. 由引理3可知TuK,且由条件(H3)得到

从而有‖Tu‖≤a,故T:Ka→Ka.

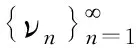
事实上,对于ν0Ka和T:Ka→Ka,有νnKa,n=0,1,2,…. 由于集合是有界的且T是全连续算子,所以集合是相对紧的. 接下来,通过归纳法证明是单调的. 首先,很明显有ν1-ν0=ν1K,这表明ν0≤ν1. 接下来,假设νk-1≤νk. 从而由条件(H4)可得

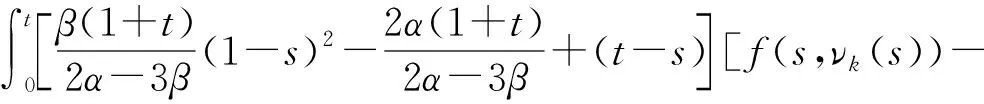
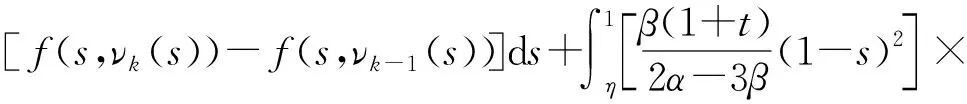
[f(s,νk(s))-f(s,νk-1(s))]ds≤b[νk(η)-νk-1(η)]×

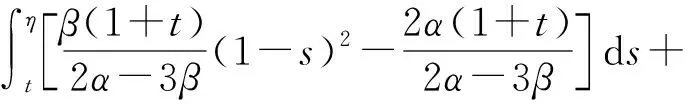
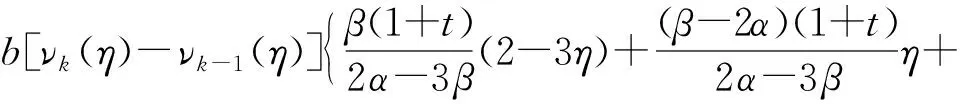
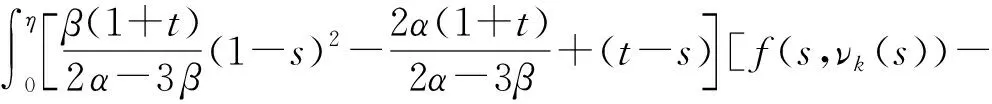
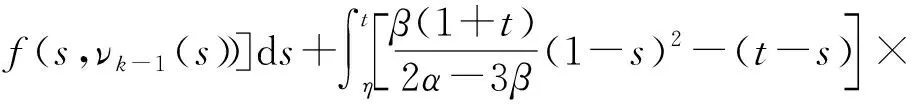
[f(s,νk(s))-f(s,νk-1(s))]ds+

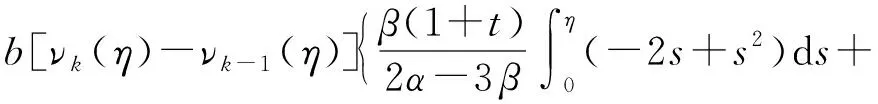
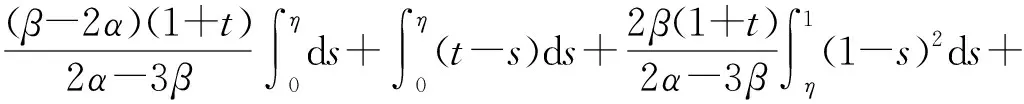
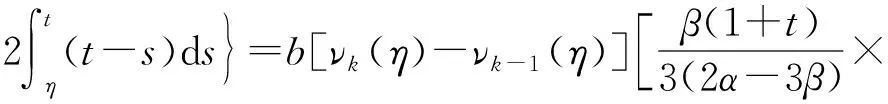
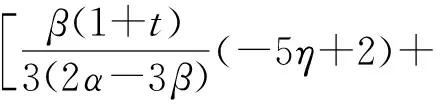
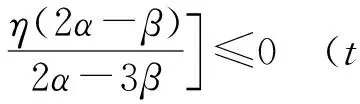
因此,

(6)

即νk+1(t)-νk(t)在[0,1]上单调递减. 与此同时,易得

(7)

从而νk+1(t)-νk(t)≥0(t[0,1]).

由式(6)和式(7)可知νk+1-νkK,则νk+1≤νk(n=0,1,2,…). 由于是相对紧集,并且是单调的,因此,必存在一个ν*Ka,使得再由T的连续性以及νn+1=Tνn可知ν*=Tν*. 这表明ν*是边值问题(1)单调递减的非负解. 此外,根据f(t,0)≠0 (t[0,1])知,0不是边值问题(1)的解,从而ν*是边值问题(1)的正解. 证毕.