焊接结构对某型金属波纹管使用寿命的影响分析
2021-04-22王升林冯震刘士杰马晓秋王慧
王升林 冯震 刘士杰 马晓秋 王慧
焊接结构对某型金属波纹管使用寿命的影响分析
王升林1冯震1刘士杰2马晓秋2王慧2
(1 北京航天动力研究所,北京,100076;2 北京航天动力研究所,低温液体推进技术实验室,北京,100076)
针对某补偿器波纹管出现的疲劳泄漏问题,开展了焊接结构对波纹管使用寿命的影响分析研究。首先,利用微结构分析的方法研究焊接结构形貌特性,并分析裂纹扩展机理,建立焊接结构的有限元模型;然后,利用子模型方法,对不同厚度焊缝的工作应力进行了计算分析,并提出波纹管焊接结构优化方案;最后,基于计算结果和疲劳寿命理论,对原始、改进波纹管焊接结构抗疲劳能力进行了分析。结果表明:1)原始焊接状态下,波纹管上封头连接环处易出现焊接缺陷,厚、薄焊缝处最大应力分别为462.84MPa和816.81MPa,超出了材料的疲劳极限,是波纹管低周疲劳破坏的主要原因;2)理想无焊接缺陷状态下,该型波纹管上封头连接环焊缝区的最大应力大约为260MPa,安全系数约为2;3)改进型波纹管连接环焊缝焊趾区最大应力为113MPa,安全系数约为4。本文的研究可为金属类波纹管的焊接结构优化和耐久性分析提供参考。
焊接结构;金属波纹管;裂纹扩展;使用寿命;仿真分析
0 前言
金属焊接波纹管是某环境控制系统补偿器的关键部件之一,它直接影响了补偿器的工作可靠性,决定了卫星中环境控制系统温控调节的成败。疲劳是焊接结构的一种典型失效模式,但目前关于波纹管类产品的焊缝、焊接工艺的分析理论还不完备,焊接结构使用寿命的评估方法还不健全。因此,开展该类金属波纹管焊接结构使用寿命的分析工作具有重要的理论与工程应用价值。
2006年,娄路亮等[1]利用有限元方法对焊接波纹管的强度、刚度和稳定性问题进行了研究,采用材料半硬化状态时拟合的本构模型和接触算法,分析发现焊接波纹管的刚度非线性主要是由材料非线性和膜片接触造成的,波纹管的最大应力出现在焊接环处,经交变载荷作用,此处最容易出现疲劳裂纹。之后,多位学者研究发现[2-5],在膜片内圆焊接处应力集中严重。2012年,Stephen等[6]利用有限元方法对金属波纹管在循环载荷作用下的失效问题进行了分析,研究发现,屈服和循环的交互作用是导致波纹管早期失效的主要原因。为了研究复杂波形焊接波纹管的设计方法,2017年,龙俞伊等[7]也对焊接波纹管的刚度、承压能力进行了分析,并利用S-N寿命曲线对焊缝的疲劳寿命进行计算,计算结果与实测值符合较好。同年,Kumar等[8,9]根据工作应力范围选择利用沉淀硬化不锈钢AM350制造波纹管,并试验优化了波纹管的焊接参数和焊接工艺,通过对波纹管的工作应力和寿命进行分析发现,优化设计后波纹管的使用寿命得到显著提升。2018年,Pavithra等[10]利用有限元方法对某U型液压波纹管的疲劳问题进行了研究,结果表明与室温相比高温下波纹管的循环寿命提高了25%,这是由于材料性质在高温下的变化导致的,而压力的增加会使波纹管循环寿命的急剧下降。
综上所述,国内外对波纹管疲劳寿命的研究较为广泛,但关于焊接结构对波纹管疲劳寿命影响的研究还较缺乏。本文针对某环境控制系统补偿器焊接疲劳泄漏问题开展研究,首先,通过观测焊缝的微结构,分析裂纹产生机理;然后,对原始波纹管进行振动环境下的应力应变分析,分析焊接结构对疲劳寿命的影响,进而提出改进方案;最后,对改进波纹管的焊接结构进行有限元计算,分析改进波纹管的安全裕度。本文的研究可为金属类波纹管的焊接结构优化和耐久性分析提供参考。
1 研究方案
本文通过试验与有限元仿真相结合的方法对波纹管疲劳泄漏问题进行了研究,分析了焊接结构对波纹管疲劳寿命的影响,提出了焊缝结构改进方案,并与原始焊接结构作了进一步的仿真对比,给出了具有针对性的建议。本文的具体研究流程,如图1所示。
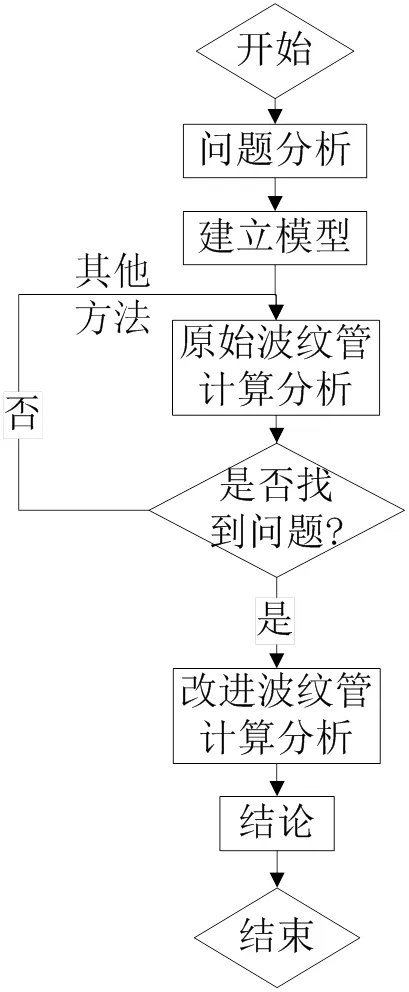
图1 研究流程
由图1可知,本文关于焊接结构对波纹管焊缝疲劳寿命影响的研究主要由三部分组成
1)泄漏机理分析
利用电镜扫描技术对原始波纹管泄漏部位的微形貌进行观测,分析裂纹附近焊接结构特点。利用高倍电镜对裂纹断口形貌观测,分析导致波纹管泄漏的机理。
2)原始波纹管建模与仿真计算
通过压痕试验确定焊缝区材料维氏硬度,预估各区材料的力学性能参数,并根据疲劳极限与强度极限的关系,获得材料的疲劳性能参数。利用三维绘图软件建立波纹管0.2°的循环对称模型和失效部位的分区子模型。利用有限元方法对不同的焊缝结构进行计算应力应变分析,研究焊缝结构对疲劳寿命的影响。
3)改进波纹管建模与仿真计算
基于(2)的结果,提出波纹管焊接结构改进方案。利用有限元方法对改进波纹管结构进行应力应变分析。对比分析原始、改进波纹管的计算结果,给出针对性建议。
2 泄漏机理分析
2.1 焊接结构观测
某环境控制系统补偿器波纹管(图2(a))随机振动力学试验中发现,在试验状态下(气—液双向压力平衡,波纹管上封头下移19mm),波纹管在66Hz附近出现相对较大的位移响应,幅值为1mm。在随后波纹管的检测当中发现焊缝处发生泄漏,泄漏位置如图2(b)所示。利用扫描电子显微镜对波纹管漏点附近区域进行了微结构观察,如图3(a)所示。同时,观测了与泄漏位置相对应的未断裂区的微结构,如图3(b)所示。
由图3可知,(1)断裂区膜片与上封头间连接的焊缝较薄,裂纹出现在焊缝上;(2)未断裂区膜片与上封头间连接的焊缝较厚,焊接部位的焊趾处存在明显的焊接缺陷;(3)焊接部位存在明显的分区,调查发现这主要是由于加工过程中的一次焊接和二次补焊引起的。这样的焊接结构容易发生疲劳断裂,王俊等[11]采用扫描电镜观测波纹管裂纹断口,发现波纹管裂开表面有明显的贝纹线,证明波纹管开裂是一种疲劳失效。为了分析造成波纹管泄漏的原因,本文开展了断口形貌观测分析。
2.2 断口形貌分析
为了对图3(a)所示的断裂区的失效机理做进一步分析,利用高倍扫描电镜对裂纹区进行观测,观测结果如图4所示。通过图4的条带宽度和裂纹深度可知,裂纹的扩展经历了大约400个当量载荷(引起可观测疲劳条带扩展的载荷),属于疲劳断裂。为了研究裂纹条带产生的时机,对原始波纹管的受载历程进行了分析,失效波纹管在整个寿命周期中经历了:16次的压并验收考核试验;24次的半程压缩热循环试验;1次力学环境考核试验。

图4 疲劳条带
通过前文分析可知,力学环境考核试验最有可能造成波纹管的疲劳断裂,这是因为:(1)验收与热循环载荷数目少,不能与疲劳条带数量对应;(2)验收和热循环试验是准静态试验,且整个过程中波纹管受压,不会造成图4所示的疲劳条带;(3)力学环境考核试验中,波纹管在66Hz附近产生1mm的位移响应。所以,本文以力学环境考核试验条件作为典型计算工况,分析波纹管焊接结构的疲劳泄漏问题。
3 波纹管建模与仿真
3.1 物性参数预估
3.1.1力学性能参数
通过压痕技术确定材料硬度,根据硬度与强度的关系确定图3(a)中各区对应的材料力学性能参数,见表1。由于波纹管在正常的工作过程中,膜片和焊缝会承受循环载荷,且结构相对较薄,会产生较大的变形和应力,因此需要膜片和焊缝具有较高的屈服强度和极限强度。
3.1.2疲劳性能参数
由设计手册[12]知,材料疲劳极限与极限强度存在的近似关系为,
焊接会导致材料疲劳强度极限降低,同时,考虑应力集中、表面加工质量,以及工艺等因素对结构疲劳强度的影响,取波纹管失效区的疲劳缺口系数为1.18。则波纹管失效区的疲劳极限为
由公式(6)、(7)得到与表1对应的各区结构的疲劳极限,如表2所示。由文献[13]可知,AM350光滑试棒的材料疲劳极限是σ-1=550MPa,与表2对比可知,所估算的焊接区材料疲劳强度极限相对合理,可用于焊接波纹管的寿命分析。
3.2 有限元建模
由图3可知,焊接部位存在明显分区。窦政平[14]的研究表明,波纹管焊缝处的确存在区别较大的分区,且各区的材料力学参数相差较大,建模应考虑各区的差异。为了降低计算量,建立了0.2°扇形焊接分区模型,如图5所示。通过瞬态计算,确定计算工况下缺陷口端A、B点的位移差,以此作为焊缝缺陷端口处的边界条件,确定该状态下焊缝的细节应力大小。
由图3可知,第一次试验中,薄焊头处发生断裂,厚焊头未发生断裂。为了对比两种类型焊头的差异,将对两种情况分别进行计算,图6分别为原始波纹管厚焊头和薄焊头形式。
其中,厚焊头包含136425个SOLID186四面体实体单元;薄焊头包含136860个SOLID186四面体实体单元。如图7所示,SOLID186是高阶3维10节点四面体单元,具有二次位移模式,可以更好的模拟不规则模型。
为了简化建模,薄焊头在厚焊头模型的基础上,仅改变焊头大小,与实物有一定偏差,但计算结果足以反映焊头厚度对疲劳寿命的影响趋势。

图5 原始波纹管焊接分区模型

表1 波纹管焊接区材料力学性能数据

表2 焊接各区疲劳强度极限

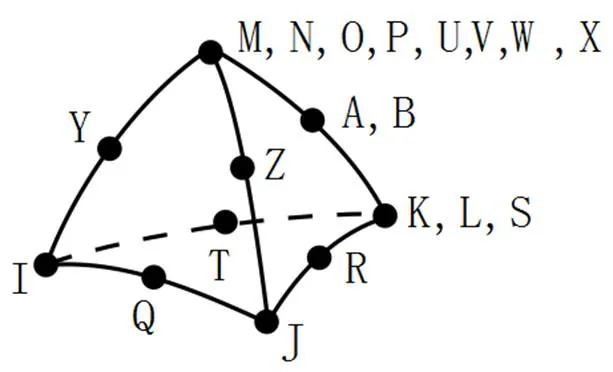
图7 SOLID186单元
3.3 问题求解
本文研究的波纹管是具有有限个自由度的弹性系统,其运动微分方程如公式(3)所示

本文不考虑结构阻尼对波纹管瞬态力学分析的影响,因此,公式(3)简化为
利用伽辽金方法对公式(4)进行离散,得到波纹管离散模型。将波纹管离散为有限个三维实体单元,分别求出每个单元的刚度矩阵为
式(6)中,为形函数矩阵,为单元质量密度。
对单元刚度矩阵和质量矩阵进行组装,得到

选取波纹管在66Hz时的一个振动周期的位移响应,将其分成多个时间段,如图8所示。
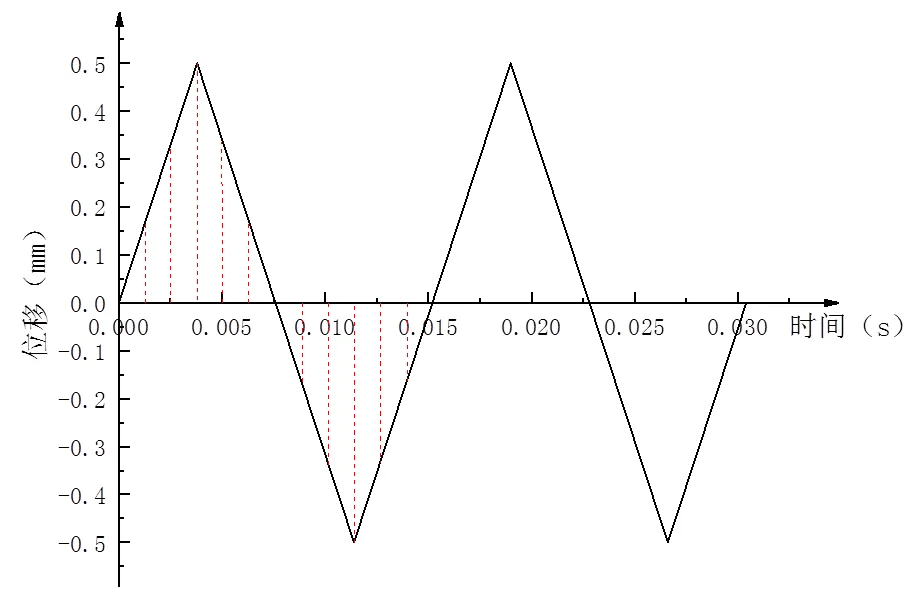
图8 66Hz下波纹管的位移响应
在每个时间段内,利用平衡迭代法计算,设置初始迭代步数为15,最小迭代步数为10,最大迭代步数为20,残差为10-5,求解考察位置的位移,图9为对应考察点的位移曲线示意图。
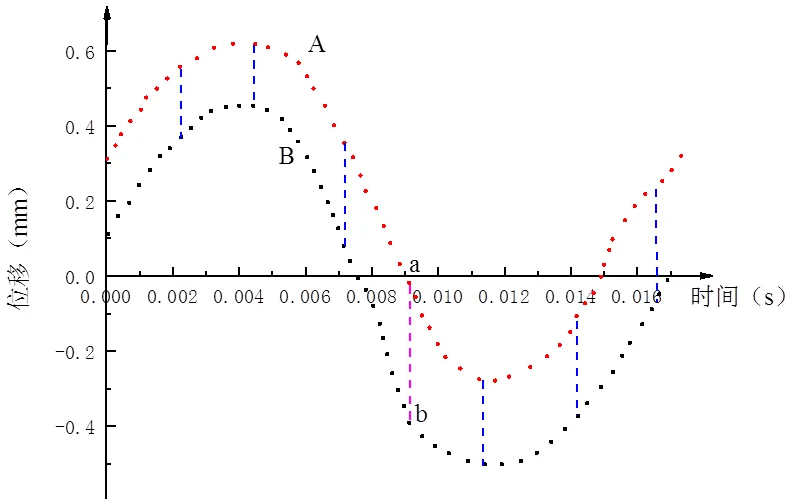
图9 A、B两点位移示意图
计算每个时间段内的A、B点位移差,取结果最大值|ab|为波纹管缺口处最大位移差。
4 结果分析
4.1 缺陷口端位移差分析
利用ANSYS软件,采用瞬态计算的方法计算图5中波纹管缺陷口端A、B点的位移差。根据振动试验条件,波纹管预压缩19mm,在66Hz的时候发现波纹管振幅为0.5mm,振动激励为13g,可计算出上封头最大速度大约为1.9m/s。由于上封头与第一道波纹管是相对运动,边界条件的施加方法是在19mm变形的基础上,给上封头一个1.9m/s的速度,波纹管和下封头保持静止状态。计算出原始波纹管A、B点的最大位移差为0.766μm。
4.2 焊缝细节力学分析
以A、B点的位移差作为焊缝缺陷口处的边界条件,计算该状态下两种焊缝的细节应力大小。原始波纹管两种类型焊头的位移与应力计算结果,见图10。
由图10可知,原始波纹管厚焊头最大应力为462MPa,略高于结构的疲劳强度极限。薄焊头局部应力高达800MPa,远高于结构的疲劳强度极限,易发生低周疲劳破坏。实际出问题焊接部位与薄焊头情况类似,所以需要引起注意。
原始波纹管不带缺陷焊接接头的计算结果,如图11所示。由图11可知,无缺陷原始波纹管焊接区最大应力为260MPa,疲劳安全系数(定义为疲劳极限与实际应力的比值)约为2。同时,在随后的波纹管力学性能试验中发现,该型波纹管可以经受2次考核试验,第3次试验中同样出现了疲劳泄漏问题。这在一定程度上反映本文的计算结果具有一定参考价值。
5 波纹管焊接结构改进与仿真计算
王战生[15]的研究表明,当焊接处膜片不水平,与封头存在倾角时,焊缝相当于存在裂纹源,会降低接头的疲劳寿命。基于此提出波纹管焊接结构改进方案,减小焊接处膜片的倾角,如图12所示。
采用图12(b)形式后,波纹管膜片与上封头连接环可以实现更好地焊接,如图13所示。
由图13可知,改进波纹管焊缝一次成型,焊接部位不存在分区,且焊缝饱满圆滑,不存在尖角等缺陷,结构更加牢固。根据改进后波纹管的结构形式,建立焊接区子模型,其模型与网格细节,见图14。共生成2130541个SOLID186四面体实体单元。
图14(a)中的数值代表区号,各区的材料属性与表1对应。振动试验条件不变,计算得改进波纹管波A、B点的位移差为2.2μm,这是由于改进波纹管焊接臂较长造成的。改进后的第一道波纹管焊接区细节应力计算结果见图15,最大应力为113MPa。
表3给出了原始、改进波纹管的Mises应力计算结果。
由表3可知,带缺陷原始波纹管缺陷区应力高于结构的疲劳强度极限,在该部位疲劳裂纹容易萌生与扩展,但试验中焊缝没有立刻被拉断的原因可能是
1)带缺陷薄焊头模型(图6(b))存在一定的建模误差,计算模型不能完全代表实物,计算结果存在偏大的情况,但对趋势分析具有借鉴意义。
2)原始波纹管在2、3焊接界面附近最大应力超过结构的疲劳强度极限,但断裂截面处的名义应力低于焊接区的疲劳强度极限,且本文未考虑塑性变形效应,应力存在一定的过估计,焊接部位具有一定的抗变形能力。
改进波纹管由于制造加工工艺较好,焊接部位应力集中现象得到明显改善,对应的细节区应力低于结构的疲劳强度极限,疲劳安全系数约为4。综上可知,在设计焊接波纹管时,应保证焊缝的厚度和形状,避免结构中存在尖角,焊缝应圆滑成形,且焊缝根部的微量间隙有助于焊缝背面成形,提高焊缝疲劳强度。

6 结论
本文利用仿真与试验结合的方法对某环境控制系统波纹管焊接结构试验后出现的泄露问题进行了研究:首先,通过扫描电镜观测到的焊接结构的微形貌特性,分析了裂纹扩展机理,在此基础上建立了不同形式的焊接结构有限元模型;然后,利用有限元方法,对不同形式焊缝的工作应力进行了计算分析,通过结果对比分析提出了波纹管焊接结构优化方案;最后,基于计算结果和疲劳寿命理论,对原始、改进波纹管的抗疲劳性能进行了分析。
通过本文的研究得出如下结论
1)波纹管的最初焊接结构厚薄不一,差异性较大。波纹管焊接结构泄漏区域观测到大约400个疲劳条带,属于低周疲劳寿命问题;
2)带缺陷原始波纹管厚、薄焊头的最大工作应力分别为463MPa和817MPa,均高于对应焊接区的疲劳极限。理想无焊接缺陷状态下,焊接区的工作应力大约为260MPa,疲劳系数约为2;
3)改进波纹管的结果和制造工艺后,焊缝的焊趾区最大应力为113MPa,安全系数约为4。
本文的研究可为该类波纹管的焊接结构优化和耐久性分析提供参考。
[1] 娄路亮, 胡晓军, 隋国发, 等. 焊接波纹管的非线性力学分析与试验研究[C]. 第九届全国膨胀节学术会议, 安徽: 中国压力容器学会膨胀节委员会、合肥通用机械研究院, 2006: 13-19.
[2] OmanS, Fajdiga M, Nagode M. Estimation of air-spring life based on accelerated experiments [J]. Materials and Design, 2010, 31 (8): 3859-3868.
[3] 王占彬, 周浩洋, 石朝锋, 等. 一种U型波纹管强度及稳定性分析方法研究[J]. 强度与环境, 2012, 39 (4): 19-24.[Wang Zhanbin, Zhou Haoyang, Shi Zhaofeng, et al. Research on the analytical method of U-shape bellows strength and stabilization[J]. Structure & Environment Engineering, , 2012, 39 (4): 19-24.]
[4] 马克, 尼加提·玉素甫, 买买提明·艾尼, 等. 大尺寸S型焊接金属波纹管刚度及薄板焊接接头应力分析[J]. 润滑与密封, 2012, 37 (12): 65-68.[Ma Ke, Nijat Yusup, Mamtimin Geni, et al. Ma Ke, Nijat Yusup, Mamtimin Geni, et al. Analysis on large-size s-shape welded metal bellow stiffness and sheet welded joint stress[J].Lubrication Engineering, , 2012, 37 (12): 65-68.]
[5] 刘江, 殷明霞, 周宏, 等. 多层波纹管结构参数与轴向刚度关系研究[J]. 强度与环境, 2016, 43 (6): 24-28.[Liu Jiang, Yin MingXia, Zhou Hong, et al. Effects of multi-layer bellows structural parameters on the axial stiffness[J]. Structure & Environment Engineering, 2016, 43 (6): 24-28.]
[6] StephenO, Jeffrey L. Failure analysis of a metal bellows flexible hose subjected to multiple pressure cycles [J]. Engineering Failure Analysis, 2012, 22: 11-22.
[7] 龙俞伊, 柴宝华, 冯波. 体积补偿用大尺寸焊接波纹管有限元分析[J]. 科技视界, 2017, 8: 51-52.
[8] Kumar Krovvidi S C S P, Sreedhar B K, Mahendran N, et al. Manufacturing experiences of large stroke welded disc bellows for nuclear applications[C]. 2017 International Conference on Advances in Mechanical, Industrial, Automation and Management Systems (AMIAMS), India, 2017: 239-244.
[9] Kumar Krovvidi S C S P, Padmakumar G, Raghupathy S, et al. Design, development and experiential validation of large stroke welded disk bellows for nuclear industry [J]. International Journal of Design Engineering, 2018, 8 (1): 57-72.
[10] Pavithra E, Senthil Kumar V S. Experimental Investigation and Numerical Analysis on Fatigue Life of Bellows [J]. Materials Today: Proceedings, 2018, 5 (9): 18848-18856.
[11] 王俊. 波纹管开裂原因分析[J]. 理化检验(物理分册), 2013, 49 (9): 632-636. [Wang Jun. Analysis on cracking cause of corrugated pipe[J]. Physical Testing and Chemical Analysis(Part A:Physical Testing), , 2013, 49 (9): 632-636.]
[12] 赵少汴. 抗疲劳设计手册[M]. 北京: 机械工业出版社, 2015: 43.
[13] AM 350 Stainless Steel: Precipitation Hardening[S]. Allegheny Technologies Incorporated, 2012.
[14] 窦政平, 姜云波, 谢志强, 等. 三层波纹管焊接与制造技术[J]. 原子能科学技术, 2005, 39: 67-72. [Dou Zhengping, Jiang Yunbo, Xie Zhiqiang, et al. Welding and manufacture technology of three-layer bellows [J]. Atomic Energy Science and Technology, 2005, 39: 67-72.]
[15] 王战生. 焊接波纹管接头设计分析[J]. 机械制造文摘(焊接分册), 2019, 3: 23-27. [Wang Zhansheng. Analysis of welded bellows joint design[J]. Welding Digest of Machinery Manufacturing, 2019, 3: 23-27.]
Analysis of the Influence of Welding Structure on the Service Life of a Certain Metal Bellows
WANG Sheng-lin1FENG Zhen1LIU Shi-jie2MA Xiao-qiu2WANG Hui2
(1 Beijing Aerospace Propulsion Institute,Beijing, 100076;2. Beijing Aerospace Propulsion Institute & Laboratory of Science and Technology on Cryogenic Liquid Propulsion, Beijing, 100076)
For the fatigue leakage problem of a certain compensator bellows, the influence of welding structure on the service life of bellows is studied in the current work. First, the microstructure analysis method is used to study the morphology of the welded structure, and the crack propagation mechanism is analyzed to establish the finite element model; Then, the working stress of the weld with different thickness is calculated and analyzed by using the sub-model method, and the optimization program of the welded structure is developed; Finally, based on the numerical results and fatigue theory, the fatigue resistance of the original and new welded structure is analyzed. The results show that: 1) Under the original welding condition, the welding defects are easy to appear at the upper joint ring of the bellows. The maximum stresses of the thick and thin welds are 462.84 MPa and 816.81 MPa respectively, both of which exceed the fatigue limit of the material and are responsible for the low cycle fatigue of the bellows; 2) Under no welding defects condition, the maximal stress at the joint zone is around 260 MPa, and the safety life coefficient is less than 2; 3) The maximum stress in the weld toe of the improved bellows joint is 113 MPa, and the safety life coefficient is 4. This research provides a reference for the welding structure optimization and durability analysis of metal bellows.
Welding structure; metal bellows; crack propagation; service life; simulation analysis
V444.3
A
1006-3919(2021)01-0032-08
10.19447/j.cnki.11-1773/v.2021.01.005
2021-01-03;
2021-01-22
王升林(1995—),男,硕士生,研究方向: 液体火箭发动机振动与热环境研究;(100076)北京市9200信箱11分箱5室.
