考虑面元转弯纤维横向约束效应的编织复合材料修正模型
2021-04-22马斌捷徐孝诚梁吉鹏周畅
马斌捷 徐孝诚 梁吉鹏 周畅
考虑面元转弯纤维横向约束效应的编织复合材料修正模型
马斌捷1徐孝诚2梁吉鹏1周畅1
(1 北京强度环境研究所,北京 100076;2北京航天长征飞行器研究所,北京 100076)
针对编织复合材料计算模型横向力学性能误差大和强度试验数据缺乏的研究现状,补充了纵横方向的刚度和强度试验数据,基于简单的刚度体积加权模型,考虑面元转弯交叉纤维的横向刚度约束效应,本文引入刚度调整因子——编织致密度,提出了面元刚度横向约束修正模型,纵横刚度和泊松比的计算误差在10%以内;结合层合板Tsai-Hill强度准则的修正模型,其纵横强度的计算误差在20%以内,获得了方法简单、较高精度的理论分析成果。
编织复合材料;强度;刚度;转弯纤维;横向约束;编织致密度;修正模型
0 引言
铺层复合材料由于高性能比和可设计性以及生产工艺方便等优点,成为高价值产品中广泛应用的先进材料之一。然而由于铺层复合材料在厚度方向缺乏高性能纤维,层与层之间只有低性能树脂粘接,在多向载荷和低能冲击条件下,容易产生分层缺陷扩展,导致承载能力降低,一定程度上影响了铺层复合材料在主承力结构上的应用。在铺层复合材料厚度方向增加穿刺纤维,可提高材料层间性能和抗分层能力,而在20世纪80年代出现的整体编织复合材料,由于存在大量斜向纤维,大大提高了编织平面的法向强度,分层问题不再存在,而且编织纤维基本为连续纤维,结构完整性大大提高,呈现出优异的抗冲击和抗疲劳性能,在工程中得到了一定的应用和发展。但编织复合材料存在两方面不足之处,一是制造工艺复杂、生产周期长、成本高,二是编织复合材料面内刚度和强度性能相比铺层材料偏低,影响了结构承载能力和工程应用范围。
要充分利用编织复合材料整体性好和性能可设计的特点,就要建立与复合材料性能和编织参数有关的编织复合材料力学性能分析模型,而编织复合材料的力学性能是结构强度分析的基础,因此该问题的研究已成为复合材料学科领域的一个热点。目前,编织复合材料力学性能研究基本上采用三种方法:1)细观力学方法以若干种典型构形单胞作为研究对象,在均匀化和直纤维假设条件下,分析不同编织参数对应的刚度性能;2)有限元方法,利用周期性边界条件,建立细观尺度的精细模型,用不同的加载形式求出对应的变形,预测材料宏观刚度参数;3)试验方法,由于理论方法还不能准确地描述编织复合材料的力学行为,试验方法更为重要,可以评价材料的基本力学性能,为理论模型提供验证。两类理论计算方法对于纵向弹性模量均比较有效,但对其它性能或是误差较大,或者缺乏试验数据的验证。从使用的方便性看,经典的细观力学方法有较大的优势,便于在工程中推广应用,在采用适当的修正系数或经验曲线后有望成为被广泛应用的方法。
编织复合材料技术目前还处于应用研究阶段,重点主要在材料力学性能的计算和预测方面,对编织复合材料的基本组成结构——单胞结构进行细观力学分析,由此分析结果才能对结构件进行宏观分析。国内外有许多学者对此问题进行了研究,Walrath[1]针对三维碳—碳材料给出了有限元分析模型;Ma[2]建立了材料性能的结构力学模型;Yang[3]和Whitney[4]提出了基于二维层合板理论的斜纤维计算模型;Hatta[5]提出了等效夹杂法的计算模型;Lei[6]基于三维桁架有限元提出了有限单胞模型;吴德隆[7-8]提出了三细胞模型,可以考虑双模量、弹塑性和损伤的影响,并且可用于五向编织材料;Mohajerjasbi[9-10]建立了编织材料力学性能和热膨胀的有限元模型;Zhong[11]提出了采用四点弯曲试验获得拉伸和压缩的应力/应变曲线,并给出了试验数据处理方法,可适用于非线性和拉、压性能不同的材料;徐孝诚[12-13]分析了细观结构的几何特征,采用空间角变换和刚度体积加权假设,纵向拉压模量计算误差在10~20%;刘振国[14-15]采用米字型模型,利用有限元方法对三维四向材料的纵、横向拉伸和剪切性能进行了数值预报;徐孝诚[16-17]对四步法编织复合材料筒壳和锥壳的外压临界载荷进行了计算和试验,试验结果与计算结果的比值在0.85~0.90之间。郑锡涛[18]采用刚度体积平均概念和体胞与面胞模型,给出了拉压模量的细观力学性能计算结果,与试验值的误差在15%以内;杨振宇[19]对面胞模型进行了修正,采用刚度体积加权平均方法,纵向模量误差在10~15%,泊松比误差超过35%;王迎娜[20]根据纤维体积含量和交叉纤维转弯特征对横向性能进行修正,提高了横向模量的计算精度,但泊松比的误差仍在20~30%;马忠辉[21]采用刚度和柔度平均方法预计了纵向模量和泊松比,误差在15%左右;徐焜[22]考虑了空间纤维束相互扭结和挤压造成的纤维束转弯和截面形状变化,纵向模量的计算精度较高,泊松比的精度也有提高,最大误差在20%左右;蔺晓明[23]分析了面胞对刚度性能的影响,仍认为纵向模量一致性较好,泊松比精度也有提高,但数据量偏少。董纪伟[24]研究了大编织角时的非线性本构关系,采用有限元细观应力分析和刚度折减方法,基于Tsai-Wu强度准则的非线性纵向强度计算误差在10%以内。卢子兴[25]分析了轴向纤维对纵向模量的增强效果,但与试验结果的误差偏大。孙颖[26]采用遗传算法对编织角和节距长度进行优化设计,获得了与测试结果一致的纵向模量,并指出了横向性能的影响因素。严实[27]考虑了纤维束的空间转弯效应,同时引入纤维束填充因子来描述纤维束截面形状对材料弹性常数的影响,纵向模量误差15%,但泊松比误差偏大。李典森[28]采用细观力学的分析方法结合桥联模型,纵向模量精度在5%以内,采用Hoffman失效准则,预报了编织复合材料的纵向拉伸强度,误差在20%以内。张芳芳[29]采用规则六面体单元建立了参数化的三维四向编织预制件网格模型,归纳出的单元切割情况共有36种,得到了与试验结果一致的纵向模量。刘振国[30]考虑了相邻纤维束之间的界面粘结效应,纤维束截面为平行六边形,有限元计算的纵向模量与试验结果一致,但泊松比误差仍在30%。姜黎黎[31]考虑空间纤维束相互挤压和扭结而造成纤维束转弯和截面形状变化,应用多相有限元法和Tsai-Wu准则,得到的编织复合材料纵向拉伸强度与试验结果的误差为15%。许善迎[32]采用刚度平均和有限元方法计算了编织复合材料的全部弹性常数,并测试三种编织角材料的纵向和横向模量及泊松比,纵向模量精度较高,横向模量误差超过25%,泊松比的误差达到20%,有限元数值方法的精度略高于刚度平均理论方法。
从编织复合材料力学性能的理论和试验研究成果看,在三个方面还存在一定的差距:一是试验数据不充分、不完全,编织方向的性能数据有一些,而横向和剪切性能数据比较少;二是分析模型与试验的一致性还不能令人满意,纵向性能基本一致,横向性能还不理想,与试验数据有差异较大;三是对刚度的研究相对较多,而对强度的研究无论从理论上还是试验上均比较少。针对编织复合材料横向刚度理论模型误差大的问题,本文以刚度体积加权模型[13]为基础,考虑编织表面转弯交叉纤维的横向约束效应,增强了面元横向刚度,并考虑编织致密度对等效弹性常数的影响,建立了一种能兼顾纵向性能和横向性能的刚度修正模型,比较了预示结果与试验结果[13]的误差,特别是与泊松比试验值的误差,并补充多种编织参数试验件的纵、横向性能刚度和强度试验数据,进一步检验修正模型的适用性,并引入应力分析和Tsai-Hill强度准则,以期获得比较准确的编织复合材料力学性能的全面预示结果。
1 考虑面元转弯交叉纤维横向约束的修正模型

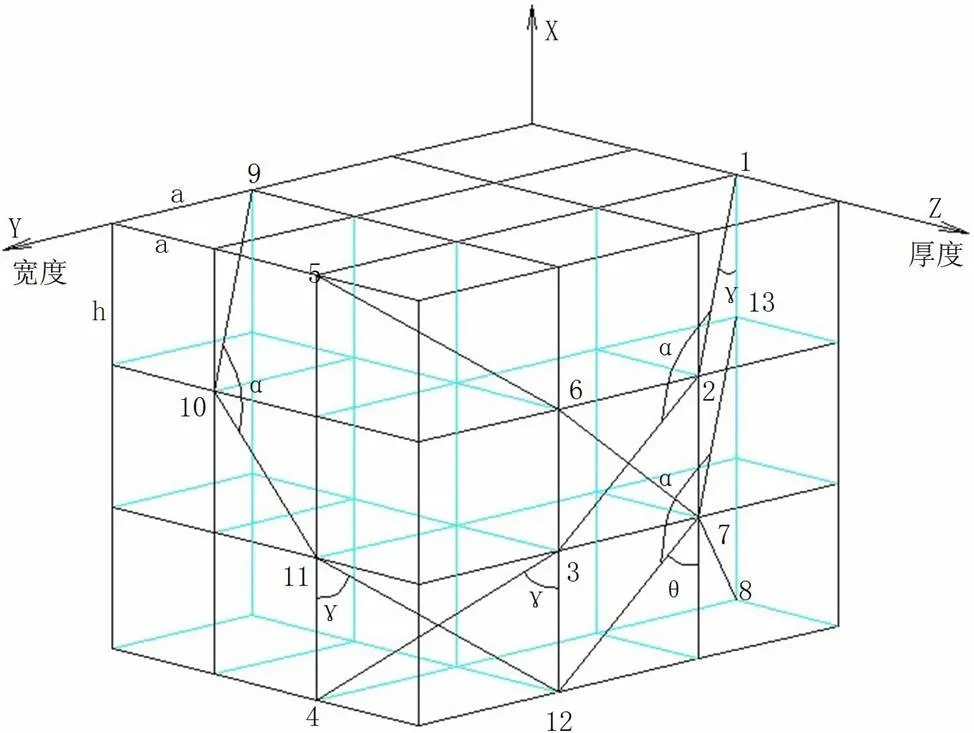
图1 纤维转弯交叉示意图

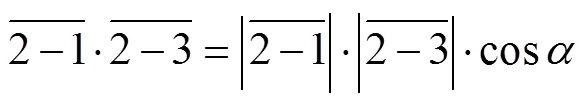

椭圆弧的外切三角形斜边的长度为

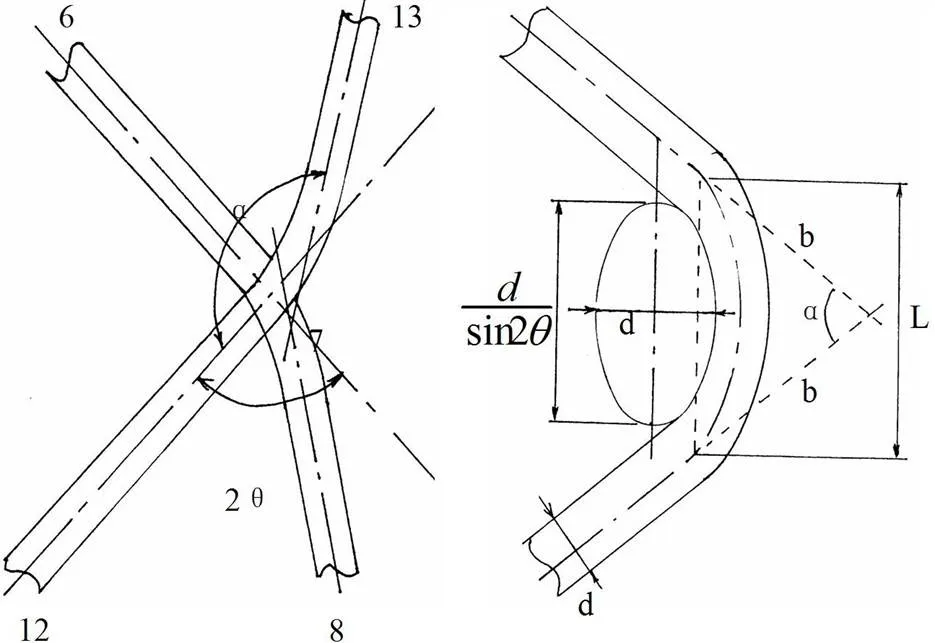
图2 面元角点处纤维交叉示意图
在7点处,13-7-12纤维和6-7-8纤维交叉在一起,这种交叉会产生对应变偏张量的约束,即对于表面角的变化有反向作用;当方向单向受拉时,、方向由于泊松效应产生收缩,使角减少,引起两束纤维互相挤压,产生反向作用力,阻止减少。从图形上看,交叉纤维受拉时,夹角减少,当交叉点无约束时,将形成图3所示的纤维转动,在方向伸长,、方向缩短,使得泊松比较大;当交叉点有约束时,横向(、方向)的缩短受到限制,形成图4所示的方向伸长、横向缩短较少的变形,使得泊松比减少,向实测值靠近。为体现出此效应,在此做一假设,将弦长为的转弯纤维投影到、方向,按投影长度将折算为平行于、轴的纤维,以增加横向刚度,减少变形,降低泊松比计算值。平行于平面的面元转弯纤维的投影长度为

平行平面的面元转弯纤维的投影长度为


设C、C为坐标轴、方向的单位长度纤维的刚度矩阵,则面元的刚度矩阵修改为
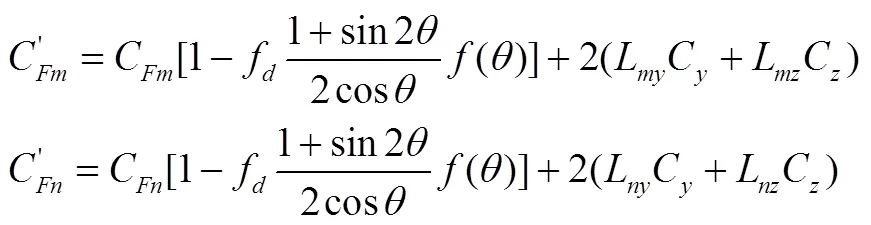

图3 交叉点无约束纤维变形
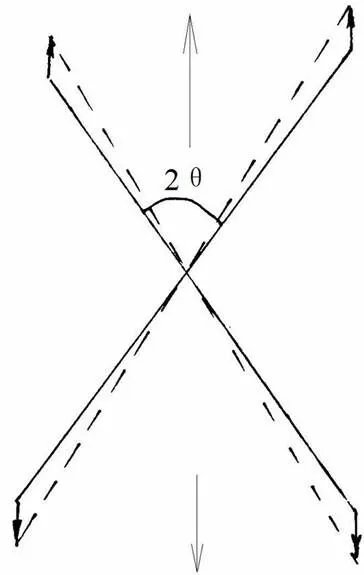
图4 交叉点有约束纤维变形
2 修正模型的刚度计算结果
为考察修正模型的效果,与试验数据[13]进行比对,试件由天津工业大学编织、北京材料工艺研究所复合并进行力学性能测试,试件采用T300(9K)碳纤维和环氧树脂制成,纤维性能参数为:f1=230GPa,f2=13.8GPa,f12=9.0GPa,f12=0.28,f23=0.44,树脂的性能为:m=4.55GPa,m=0.34,采用复合材料单向板细观力学方法[34-35],计算对应纤维体积含量的单向板弹性常数,纤维方向模量和泊松比采用并联算法,其它参数采用Halpin-Tsai公式。对刚度体积加权模型[13]按上节方法进行修正,可得出各种试件的工程弹性常数计算结果(见表1)。与试验结果相比可以看出,修正模型的E值对于32°和21°试件更接近于试验值,37°和25.5°试件的计算值与体积加权模型相当。修正模型的泊松比与试验值基本一致,比体积加权模型的精度高的多,说明转弯纤维的交叉挤压效应对材料横向刚度的影响必须考虑,各种参数的计算误差在10%以内。从横向弹性模量E看,修正模型对于各种试件的预示精度都有所提高,体现出对横向性能的增强,编织角增大,增强量也增大。从剪切模量G看,修正模型的预示值比体积加权模型稍降低一些,编织角大的降低稍多一些。这种结果也说明面元对横向刚度的贡献大一些,面元刚度矩阵的修正对泊松比和横向刚度的影响比较明显,基元对剪切刚度的贡献比面元大,修改面元对剪切刚度影响不明显。
为验证修正模型对编织复合材料横向性能的适用性,并补充横向性能的试验数据,设计生产了两种宽度的纵向和横向编织复合材料切边试件,均是从宽板上切割而成的,即侧面面元数2=0,进行了纵向和横向的拉伸和压缩试验;为比较弯曲时拉、压区性能的差异,进行了四点弯曲试验;为研究单种结构细胞元素的特性,将试件表面的面元铣切去除,进行了纯基元的拉伸试验。补充试件仍由天津工业大学编织、北京材料工艺研究所复合并进行力学性能测试,材料和工艺未变。补充试验结果(表2)的分散性与铺层复合材料相比偏大一些,相当一部分参数的变差系数在10~15%之间,拉伸与压缩模量略有差别,拉压泊松比也有一定的差异,宽试件的模量和强度略高于窄试件,由于数据分散性较大,宽度的影响不显著。表2中四点弯曲和纯基元拉伸的试件与表1中的拉伸试件编织参数相同,但不是同批次生产的,纤维排列比较紧密,单位长度内的纤维编织花节数高于切边试件,即编织致密度有差异,经试算切边试件取f=0.35的计算结果与试验是一致的(表3),纵横模量和泊松比的计算误差在10%以内,只有四面铣切的基元拉伸试件的泊松比有一定的差异,其原因是试件的基元未完全铣掉,约束了泊松效应。此结果从纵向和横向性能两个方向验证了修正模型对于三维四向编织复合材料刚度预测的适用性,修正模型在不同的编织角、纤维含量、编织致密度、载荷方向等条件下均得到了与两批次试验一致的计算结果。

表1 几种试件的试验结果和修正模型刚度计算结果
注:表中“/”后的百分数为试验结果的变差系数

表2 补充的编织复合材料试验结果统计表
注:1)表中“/”后的百分数为试验结果的变差系数;2)序号9的试验结果前为拉伸区数据,后为压缩区数据

表3 补充试件刚度试验和修正模型的计算结果
* 弯曲状态下拉伸区试验数据;** 弯曲状态下压缩区试验数据
3 编织复合材料的强度分析
编织复合材料的强度分析需要三个方面的条件,一是应力计算,二是单向板强度参数,三是适当的强度准则。应力计算的基础就是修正模型和刚度矩阵C或柔度矩阵S=C-1,由应力张量可得出总应变为[13]
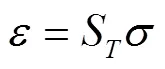

设编织材料中的斜向纤维的空间角[13]为和,斜纤维自身坐标系中的应力与总体坐标系中的应力变换矩阵为(),假设编织材料的应变是均匀的,则斜纤维在自身坐标系中的空间应变张量为[34-35]
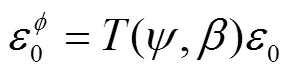
空间总应变为

由单向杆在自身坐标系中的刚度矩阵可得[13],斜纤维在自身坐标系中的空间应力张量为
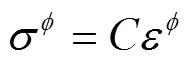
编织材料的强度与复合材料单向板的强度密切相关,由于编织材料的纤维体积比V受编织角影响,其变化范围比单向板大,一般单向板的V在60%左右,强度数据是对于60%体积比试件的,而补充试件的V为55~62%,使用60%的数据会引入误差,本文按单向板数据[34]和强度预测关系式近似给出不同V下的单向板强度值(MPa)为T=1360V/0.6,X=1130f/0.6,Y=42.3V/0.6,Y=187f/0.6,=62V/0.6,为单向板剪切强度,对应的应力为12、13,23对应层间剪切强度S,假设90°层间剪切强度为0°的一半,S与层间夹角是余弦关系,即
取45°夹角时的S作为23对应的强度,则S=0.8535S。由于编织材料的纤维均处于三维应力状态,不能采用一次强度准则,应采用二次强度准则。单向板在二向应力状态下目前还没有令人满意的强度准则,因此对编织材料不能奢望准确的强度准则,应采用比较简单的形式,本文选用层合板复合材料的Tsai-Hill准则进行强度校核,将平面内的准则,推广到空间三维状态,强度准则为
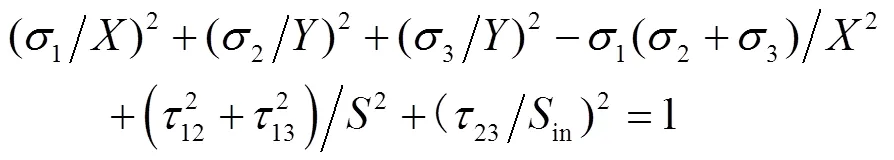
按以上方法对补充试件进行计算,以正应力的符号确定各个方向的强度是拉伸强度还是压缩强度,补充试件的强度试验结果与计算值比较一致(表4)。

表4 补充试件的编织复合材料强度试验和计算结果
* 弯曲状态下压缩区试验数据
各种试件的纵、横强度与计算值均比较接近,差异基本在20%以下,仅两种宽度切边试件试验结果只有纵向拉伸强度相差超过25%,说明强度测试结果和计算方法是可信的。结合层合板Tsai-Hill准则的刚度修正模型,根据单向板强度数据和编织参数,可以用于三维四向编织复合材料的各项强度性能预测。
4 结束语
力学性能计算模型是编织复合材料应用的基础,本文补充了目前文献中缺乏的横向模量和强度试验数据,依据最为简单的体积加权模型[13],考虑到表面纤维转弯交叉效应对横向刚度的贡献,引入层合板复合材料中的应力计算方法和Tsai-Hill强度准则,得出了与试验结果一致的强度和刚度计算结果,方法简单,概念明确,结果正确,综合效果高于大部分理论模型,可以用于编织复合材料力学性能的细观力学分析和性能预测。由于试验数据相对较少,有一定的离散性,参数变化范围有限,本文方法的有效性有待于今后更多的试验数据的验证,还需要补充剪切模量和强度数据进行进一步的验证或修正。试验结果的分散性说明材料编织和复合的工艺质量稳定性有待提高,应重视工艺过程对材料性能的影响,以促进编织复合材料在工程结构中的广泛应用。
[1] Walrath D E, Admas D F. Finite Element Micromechanics and Mini-mechanics Modeling of a Three-dimensional Carbon-carbon Composite Material[R]. AD-A168050, 1985.
[2] Ma C L, Yang J M, Chou T W. Elastic stiffness of three-dimensional textile structural composite[C]. ASTM STP 893, Composite Materials-Testing and Design, 1986: 402-421.
[3] Yang J M, Ma C L, Chou T W. Fiber inclination model of three dimensional textile structural composites [J]. J. Comp. Mat., 1986(20): 472-483.
[4] Whitney T J, Chou T W. Modeling of 3-d angle-interlock textile structural composite [J]. J. Comp. Mat., 1989: 890-911.
[5] Hatta H. Elastic moduli and thermal expansion coefficients of three dimensional fabric composites[J]. J. of the Japan Society for Composites Materials, 1988, 14(2): 73-80.
[6] Lei C, Cai Y J, Ko F. Finite element analysis of 3-d braided composites[J]. Advances in Engineering Software, Elsevier Science Publishers, 1992: 187-194.
[7] 吴德隆,郝兆平.五向编织结构复合材料的分析模型[J]. 宇航学报,1993,14(3):40-51.[Wu Delong,Hao Zhaoping.5D braided structural composites[J].Journal of Astronautics,1993,14(3):40-51.]
[8] Wu D L. Three-cell model and 5-D braided structural composites[J]. Composites Science and Technology, 1996, 56(3): 225-233.
[9] Mohajerjasbi S. Prediction for coefficients of thermal expansion of three-dimensional braided composites[J]. AIAA Journal, 1997, 35(1): 141-144.
[10] Mohajerjasbi S. Fiber Architecture of three-dimensional braided composites[J]. AIAA Journal, 1998, 36(4): 613-617.
[11] Zhong Y,Sikarskie D L.On a Technique for generating stress strain curves from flexural data[J]. J.Comp. Mat., 1996, 30(9): 966-983.
[12] 徐孝诚, 孙德海, 黄小平. 三维编织复合材料细观结构的几何学分析[J]. 强度与环境, 1999(2): 37-43. [Xu Xiaocheng, Sun Dehai, Huang Xiaoping. Geometry analysis on microstructure of 3-D braided composite. [J]. Structure & Environment Engineering , 1992(2): 37-43.]
[13] 徐孝诚, 黄小平, 孙德海. 三维编织复合材料力学性能分析与预估[J]. 强度与环境, 2000(4): 22-29. [Xu Xiaocheng, Huang Xiaoping, Sun Dehai. Analysis and predication on the mechanical properties of 3D braided composite. [J]. Structure & Environment Engineering, 2000(4): 22-29.]
[14] 刘振国, 陆萌, 麦汉超, 等. 三维四向编织复合材料弹性模量数值预报[J]. 北京航空航天大学学报. 2000, 26(2): 182-185.[Liu Zhenguo, Lu Meng, Mai Hanchao. Numerical prediction of moduli of 3-D and 4-step braided composites [J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(2): 182-185.]
[15] 刘振国, 卢子兴, 陆萌, 等. 三维四向编织复合材料剪切性能的数值预报[J]. 复合材料学报. 2000, 17(2): 66-69.[Liu Zhenguo, Lu Zixing, Lu Meng, et al. Numerical prediction of the longitudinal and transversal moduli of three dimensional and 4-step braided composites[J]. Acta Materiae Compositae Sinica, 2000, 17(2): 66-69.]
[16] 徐孝诚, 马斌捷. 三维四向整体编织复合材料圆筒壳体临界外压计算及试验验证[J]. 复合材料学报, 2002, 19(4): 92-95.[Xu Xiaocheng, Ma Binjie. Critical external pressure calculation and test validation of 3D 4-step braided composite cylindrical shell [J]. Acta Materiae Compositae Sinica, 2002, 19(4): 92-95.]
[17] 徐孝诚, 孙鹏军, 马斌捷, 等. 三维四向整体编织碳/环氧复合材料圆锥壳体的外压稳定性研究[J]. 强度与环境, 2002, 29(1): 17-19, 34.[Xu Xiaocheng, Sun Pengjun, MA Binjie, et al. External pressure stability research of 3D 4-Step braided carbon/epoxy composite conical Shell[J]. Structure & Environment Engineering , 2002, 29(1): 17-19, 34.]
[18] 郑锡涛, 叶天麒. 三维四向编织复合材料弹性性能细观分析[J]. 机械强度, 2003, 25(5): 504-508.[Zheng Xitao, Ye Tianqi. Microstructure analysis on the elastic behavior of 3D braided composites[J]. Journal of Mechanical Strength, 2003, 25(5): 504-508.]
[19] 杨振宇, 卢子兴. 三维四向编织复合材料弹性性能的理论预测[J]. 复合材料学报, 2004, 21(2): 134-141.[Yang Zhenyu, Lu Zixing. Theoretical prediction of the elastic properties of three-dimensional and four-directional braided composites[J]. Acta Materiae Compositae Sinica, 2004, 21(2): 134-141.]
[20] 王迎娜, 王玉林, 万怡灶. 三维四向编织复合材料体胞模型的修正[J]. 复合材料学报, 2004, 21(2): 128-133.[Wang Yingna, Wang Yuling, WAN Yizao. Modifying of global-cell model of 3-D and 4-Step braided composites[J]. Acta Materiae Compositae Sinica, 2004, 21(2): 128-133.]
[21] 马忠辉, 孙秦. 三维四向编织复合材料有效弹性模量的预测[J]. 机械科学与技术, 2004, 23(11): 1334-1337.[Ma Zhonghui, Sun Qin. Prediction for effective elastic moduli of three-dimensional braided composites[J]. Mechanical Science and Technology, 2004, 23(11): 1334-1337.]
[22] 徐焜, 许希武, 汪海. 三维四向编织复合材料的几何建模及刚度预报[J]. 复合材料学报, 2005, 22(1): 133-138. [Xu Kun, Xu Xiwu, Wang Hai. On geometrical model and stiffness prediction of 3D 4-Directional braided composites [J]. Acta Materiae Compositae Sinica, 2005, 22(1): 133-138.]
[23] 蔺晓明, 刘振国, 卢子兴. 三维编织复合材料弹性性能的表面胞体效应[J]. 复合材料学报, 2006, 23(6): 168-173.[Lin Xiaoming, Liu Zhenguo, Lu Zixing. Effect of surface cell on elastic properties of 3D braiding composites[J]. Acta Materiae Compositae Sinica, 2006, 23(6): 168-173.]
[24] 董纪伟, 孙良新, 洪平. 三维四向大编织角复合材料的细观强度分析[J]. 材料科学与工程学报, 2006, 24(4): 539-542. [Dong Jiwei, Sun Liangxin, Hong Ping. Micro strength analysis of 3D 4-Directional braided composites with large braiding angle[J]. Journal of Materials Science and Engineering, 2006, 24(4): 539-542.]
[25] 卢子兴, 刘子仙. 三维五向编织复合材料的弹性性能[J]. 北京航空航天大学学报, 2006, 32(4): 455-460.[Lu Zixing, Liu Zixian. Elastic properties for 3 dimensional and 5 directional braided composites[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(4): 455-460.]
[26] 孙颖, 李嘉禄. 三维四向编织复合材料刚度的细观力学设计[J]. 纺织学报, 2007, 28(5): 70-73.[Sun Ying, Li Jialu. Stiffness optimization of 3-D braided composites with micromechanical method[J]. Journal of Textile Research, 2007, 28(5): 70-73.]
[27] 严实, 吴林志, 孙雨果, 等. 三维四向编织复合材料有效性能的预报[J]. 复合材料学报, 2007, 24(1): 158-166. [Yan Shi, Wu Linzhi, Sun Yuguo, et al. Evaluation of elastic properties of 3D 4-directional braided composites[J]. Acta Materiae Compositae Sinica, 2007, 24(1): 158-166.]
[28] 李典森, 卢子兴, 卢文书. 三维四向编织复合材料刚度和强度的理论预测[J]. 应用数学和力学, 2008, 29(2): 149-156. [Li Diansen, Lu Zixing, Lu Wenshu. Theoretical prediction of the stiffness and strength of three-dimensional and four-directional braided composites[J]. Applied Mathematics and Mechanics, 2008, 29(2): 149-156.]
[29] 张芳芳, 姜文光, 刘才. 三维四向编织复合材料参数化单胞模型建立及弹性规律数值预测[J]. 机械工程学报, 2014, 50(8): 87-94. [Zhang Fangfang, Jiang Wenguang, Liu Cai. Numerical Prediction of Elastic Properties Law for 3D Four-directional Braided Composites with Parametric Unit Cell Model[J]. Journal of Mechanical Engineering, 2014, 50(8): 87-94.]
[30] 刘振国,商园春, 董阿鹏, 等. 三维四向编织复合材料改进模型弹性性能计算[J].北京航空航天大学学报, 2014, 40(1):1-5. [Liu Zhenguo, Shang Yuanchun, Dong Apeng, et al. Elastic properties computation for three-dimensional and four-directional braided composites based on an improved model[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(1):1-5.]
[31] 姜黎黎, 徐美玲, 王幸东, 等. 复杂载荷作用下的三维编织复合材料力学性能分析[J]. 哈尔滨理工大学学报, 2018, 23(4): 108-112. [Jiang Lili, Xu Meiling, Wang Xingdong, et al. Mechanics analysis of 3D braided composites under complex loadings[J]. Journal of Harbin University of Science and Technology, 2018, 23(4): 108-112.]
[32] 许善迎, 谭焕成, 关玉璞, 等. 三维四向编织复合材料力学性能预测及实验验证[J]. 材料工程, 2018, 46(6): 132-140.[Xu Shanying, Tan Huancheng, Guan Yupu, et al. Predication and experimental verification on mechanical properties of three-dimensional and four-direction braided composites[J]. Journal of Materials Engineering, 2018, 46(6): 132-140.]
[33] 北京矿业学院高等数学教研组. 数学手册[M]. 北京: 煤炭工业出版社, 1976.
[34] 张骏华, 盛祖铭, 孙继桐. 复合材料结构设计指南[M]. 北京: 宇航出版社, 1999.
[35] 航空航天工业部科学技术研究院. 复合材料设计手册[M]. 北京: 航空工业出版社, 1990.
Modified Model of Braided Composites Considering Transverse Restraint Effect of Turning Fibers on Surface Cell
MA Bin-jie1XU Xiao-cheng2LIANG Ji-peng1ZHOU Chang1
(1 Beijing Institute of Structure and Environment Engineering, Beijing 100076, China;2 Beijing Institute of Space Long March Vehicle, Beijing 100076, China)
On account of the research status of braided composites, large errors of transverse mechanical properties in calculation model and lacking of strength test data, the stiffness and strength test data in longitudinal and transverse directions are supplemented, based on the simple stiffness volume weighted model, the transverse stiffness constraint effect of turning fibers on surface cell is considered, stiffness adjustment factor-braiding density is introduced in this paper, modified model of the surface cell stiffness with transverse constraint is proposed, and the calculation errors of longitudinal and transverse stiffness and Poisson's ratio are within 10%. Combined with modified model of Tsai-Hill strength criterion, the calculation error of longitudinal and transverse strength is less than 20%, and the theoretical analysis results with simple method and high accuracy are obtained.
Braided composites; strength; stiffness; turning fibers; transverse constraint; braiding density; modified model
V415
A
1006-3919(2021)01-0001-09
10.19447/j.cnki.11-1773/v.2021.01.001
2021-01-03;
2021-01-22
自然科学基金(11502024)
马斌捷(1961—),男,研究员,研究方向: 结构强度;(100076)北京市9200信箱72分箱11号.
