复杂应力状态下7085铝合金失效破坏试验与数值研究

刘彦杰 高小青 李明强

复杂应力状态下7085铝合金失效破坏试验与数值研究

刘彦杰 高小青 李明强

（航空工业第一飞机设计研究院 西安 710089）

本文在损伤力学和金属延性断裂理论的框架下，通过设计多种局部细节特征的元件级试验件，研究7085铝合金材料在不同应力状态下的破坏性能。通过试验与有限元分析相结合，建立7085铝合金材料断裂塑性应变与应力状态参数（应力三轴度）间的关系，作为金属材料失效判据。最后，通过接头结构破坏试验，验证失效判据的预测精度，试验与数值仿真结果表明通过本文设计的元件级试验件获取的材料应力三轴度-断裂应变失效判据能有效预测复杂应状态下接头结构的失效行为。

复杂应力状态；接头结构；延性断裂；断裂应变失效准则；有限元分析

0 引言

现代飞行器日益复杂的结构形式和载荷作用，对飞行器结构精细化设计提出了极高的要求。对金属主承力结构，诸如关键接头、加强框等实体结构的极限承载能力以及破坏形式进行高精度数值预测是金属主承力结构精细化设计与验证的关键。然而，现行工程设计手段主要依赖经验公式以及标准材料断裂性能进行粗定量分析，难以对具有复杂细节特征的结构进行高精度失效破坏分析。

金属实体结构的失效破坏属于金属材料在复杂应力状态下的破坏行为。试验与理论研究表明，金属材料在复杂应力状态下的破坏行为有别于单一应力状态下材料的破坏行为，呈现出与应力状态强相关的特性。因此研究金属材料在复杂应力状态下的破坏行为，建立复杂应力状态下金属失效模型是进行金属结构失效破坏数值分析的关键。

国内外试验和理论研究表明应力三轴度是影响金属延性断裂性能最重要的应力状态参数[1-15]。早期试验研究揭示了静水应力（或应力三轴度）对金属材料的塑性演化以及破坏应变有着重要的影响，基于单一曲线假设的J2强度理论并不能准确描述材料在复杂应力状态下的失效行为。在试验研究的基础上，Johnson和Cook提出了Johncon-Cook断裂模型（J-C模型）[1]，该模型虑及了应力三轴度、应变率以及温度对塑性演化及破坏的影响。J-C模型认为材料断裂应变随应力三轴度的增加单调递减。Wilkins[2]以及Wierzbicki等人[3-5]在总结前人试验基础上发现应力三轴度并非单调地影响材料破坏应变，从而提出了多种新型的考虑应力状态参数影响的金属延性断裂模型。但上述研究大多通过三维拉伸应力状态下的元件试验进行，缺少更为广范围的应力三轴度试验及破坏数据，导致上述模型对材料在某个应力三轴度范围内的断裂行为有很高的预测精度，对其它应力三轴度范围的预测精度则不好。所以，深入地研究应力三轴度对金属材料破坏行为的影响仍十分必要。

本文对航空航天领域常用的7085铝合金材料在复杂应力状态下的失效破坏行为进行了试验与数值分析，研究7085铝合金材料的破坏行为随应力三轴度的变化规律，并进行相应有限元数值破坏分析与验证。主要研究内容包括以下三方面：（1）设计不同应力三轴度范围的元件级试验件，并针对7085铝合金材料，获取不同应力三轴度下材料的破坏试验数据；（2）根据获取的不同应力状态下的材料破坏试验数据，建立材料断裂应变与应力三轴度的关系曲线；（3）结合试验与有限元手段，将材料断裂应变与应力三轴度的关系曲线作为材料失效判据进行有限元失效分析；（4）通过典型接头破坏试验，对比破坏试验与有限元失效分析结果，验证本文方法预测接头结构极限承载能力与断裂位置的有效性。

1 元件级试验研究

试验研究表明应力三轴度参数对金属材料破坏行为具有重要影响。本文以应力三轴度为应力状态表征参数，根据不同应力三轴度范围区间，设计了三类元件级试验件，用于获取材料在不同应力状态下的破坏性能数据，用以建立7085铝合金材料的延性断裂模型。

元件级试验件包括三大类构型，分别为圆柱单轴压缩试验件、板材剪切试验件以及光滑、缺口圆棒单轴拉伸试验件。各类试验件所对应的应力三轴度参数范围如图1所示。应力三轴度参数的定义如公式1所示，即平均应力与等效应力（即Mises应力）之比。

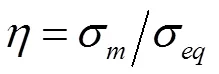
通过这些试验并结合有限元数值分析，获取材料在不同应力三轴度下的破坏性能数据，由此可进一步获得可用于分析金属在复杂应力状态下破坏的延性断裂曲线。

1.1 试验件设计

根据应力三轴度范围的定义（见图1），本节选取圆柱压缩、板材拉剪、光滑/缺口圆棒拉伸试验分别用于获取压剪复合（低应力三轴度）、拉剪复合（中应力三轴度）以及三维拉伸（高应力三轴度）下的材料破坏性能。

1.1.1圆柱单轴压缩试验（低应力三轴度情况）

低应力三轴度范围主要指应力三轴度从-1/3 到 0 的应力状态范围。该试验在材料万能试验机上进行。采用4种不同直径—长度比的短圆柱试件进行轴向压缩试验（如图2所示）。每种试件直径Φ均为12mm，试验件长度分别为24mm、15mm、12mm和8mm。

图2 单轴压缩试验件实物图

1.1.2 板材剪切试验（中应力三轴度）

中应力三轴度范围主要指应力三轴度从0到1/3的应力状态范围。该试验在拉伸试验机上进行。试验件采用整体尺寸为 150mm×35mm×2mm 带有一定缺口角度的平板试件（如图3所示）。当缺口轴线与试件拉伸轴线重合时（缺口角度定义为0°），缺口部分的受力状态接近于纯剪切应力状态，应力三轴度接近于0。

初始缺口角度会影响拉伸时缺口部分的受力状态，一般地随着初始缺口角度的增大，受力状态由纯剪切向拉剪复合状态转变。因此为了丰富不同应力状态的试验数据，本试验采用初始缺口角度为0°、30°和60°三种剪切试件。

图3 板材拉剪试验件实物图

1.1.3 光滑/缺口试件单向拉伸试验(高应力三轴度)

高应力三轴度范围主要指应力三轴度在 1/3 以上的应力状态范围。该试验在拉伸试验机上进行。试件分为光滑试件和缺口试件两类（如图4所示）。光滑拉伸试件有效尺寸为Φ9×90，用于获得材料标准应力—应变曲线。缺口拉伸试件选用了四种试件，即缺口半径分别为3mm，5mm，7mm 和 9mm，并保持每种试件的最小截面直径为6mm。

图4 光滑圆棒和4种缺口圆棒元件级试件实物图

1.2 试验结果

7085铝合金材料元件级试验的主要试验结果包括：材料应力应变曲线以及各构型试验件断裂时刻位移结果。前者作为有限元弹塑性分析的输入条件，后者结合有限元分析获取各构型试验件断裂塑性应变与应力三轴度数据，最终用于材料失效模型的建立[6, 13]。

1.2.1 材料应力应变曲线

表1 7085铝合金材料弹塑性常数

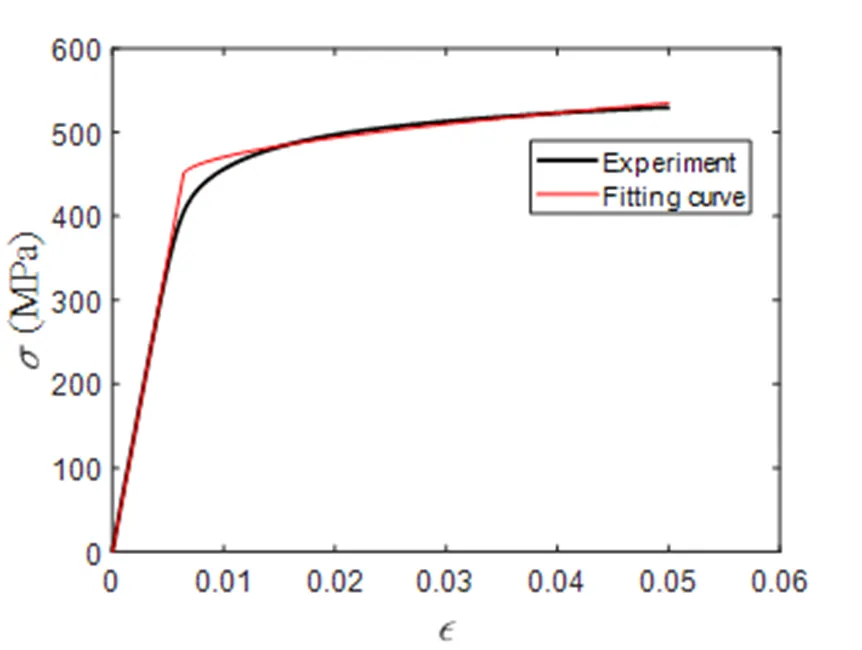
图5 7085铝合金材料应力应变曲线

1.2.2试验件断裂时刻位移结果

根据各类元件级试验件载荷—位移曲线的斜率突变来判断试验在加载过程中发生断裂的时刻。7085铝合金材料各类元件级试验件断裂时刻位移如表2所示。

2 材料断裂失效模型建立

2.1 试验件断裂应变与应力三轴度数据获取

对各类元件级试验进行有限元建模，将光滑圆棒试验获得的材料应力应变曲线代入各类元件级试验件有限元模型中计算，参考试验过程中的断裂位移（或虚拟引伸计），提取有限元模型中断裂发生时刻的塑性应变和平均化的应力三轴度，得到各试验件应力三轴度—断裂应变关系，见表3（表中应力三轴度为平均应力三轴度）。

平均应力三轴度由积分求得，积分路径为塑性起始时刻到断裂失效发生时刻的应变路径，即

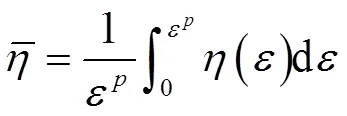
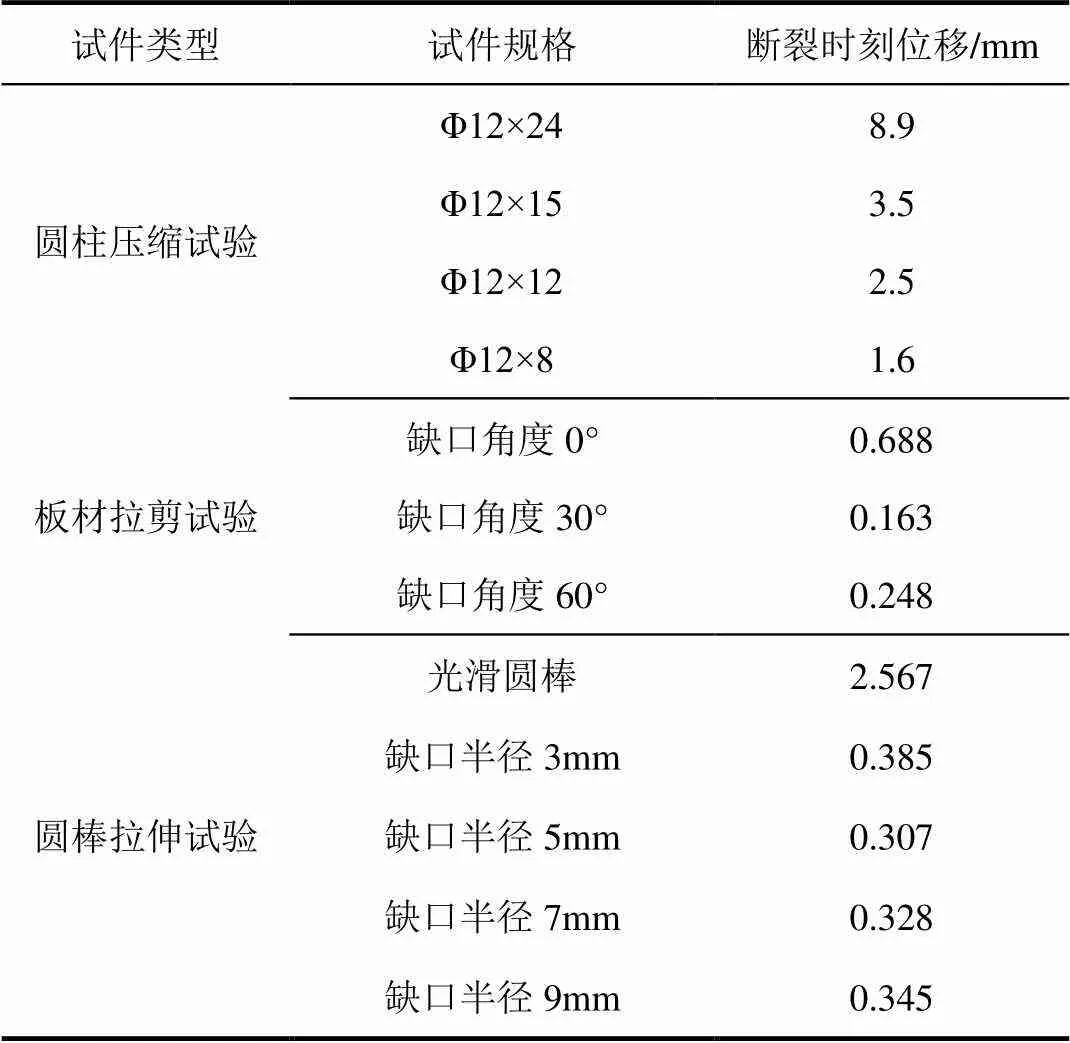
表2 7085铝合金元件级试验断裂时刻位移结果

表3 7085铝合金元件级试验应力三轴度-断裂应变关系

2.2 材料断裂应变与应力三轴度关系拟合

由试验结果可知，7085铝合金材料呈现明显的拉伸脆性、压缩塑性的特性，其低应力三轴度下的断裂应变比中、高应力三轴度下的断裂应变高，这种情况下可利用J-C失效模型对所有数据点进行拟合

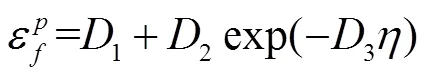
图6 7085铝合金应力三轴度-断裂应变曲线

Fig. 6 The traxiality-fracture strain curve of AL 7085

3 接头结构破坏试验与有限元数值验证

3.1 接头破坏试验结果

为验证7085铝合金材料失效模型的预测精度，本文对典型接头试验件进行拉伸破坏试验。通过典型接头破坏试验与数值分析的对比研究，验证本文建立的结构失效有限元数值分析方法以及其在预测裂纹萌生位置和破坏载荷等方面的精度。试验件结构如图7所示，整体尺寸约为160mm×140mm×80mm。

试验件通过夹具连接并放置于试验机上进行单轴拉伸加载。试验加载时，按图7中所示的坐标系，从原点处加载，加载方向在XOZ平面内，且与X轴呈20度角斜向上。试验件夹具及加载如图8和图9所示。铝合金接头破坏试验共有3个相同规格试验件进行重复试验。破坏试验结果显示各试验件的破坏形貌一致（如图10所示），破坏载荷基本一致。各试验件拉伸载荷—位移曲线如图11所示，每个试件的最大载荷和断裂位移统计结果如表4所示。

3.2 接头破坏试验有限元验证

本文采用ABAQUS/Explicit显式求解器进行准静态求解，通过单元删除法模拟裂纹产生与扩展[6,7,12]。具体而言，首先建立典型接头及夹具的有限元模型，然后将7085铝合金材料的弹性模量、泊松比以及弹塑性本构曲线赋给接头模型，并在材料属性设置时选择延性断裂失效模型（ductile fracture），将图6所示的应力三轴度—断裂应变曲线作为材料失效判据赋给接头有限元模型，最后设置约束与载荷（本文选取位移加载方式）进行显式动力学准静态求解。求解过程中需控制加载速率，保证模型总动能占总能量比值不超过10%，以满足准静态求解的精度。

图7 接头试验件示意图

图8 接头试验件夹具及加载示意图

表4 7085铝合金典型接头破坏试验参数

图9 接头试验件及夹具现场安装图

图10 铝合金典型接头试验件断裂后照片

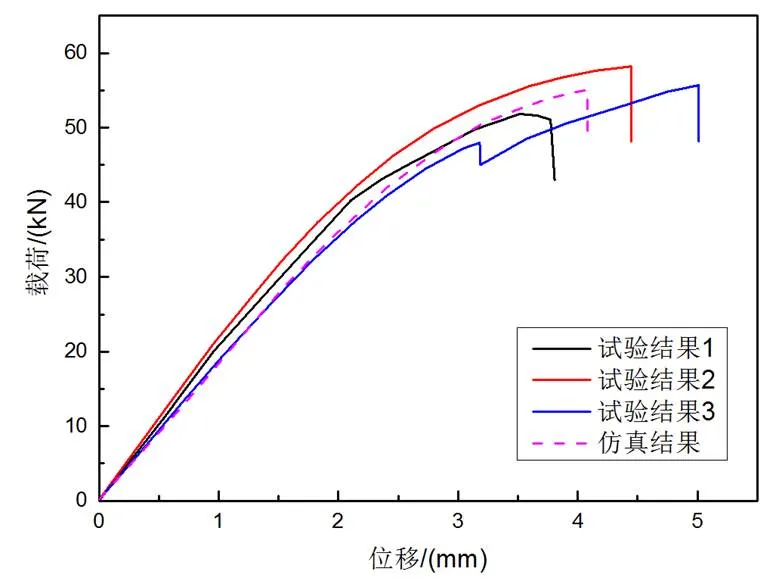
图11 铝合金接头破坏试验与数值仿真载荷—位移曲线

接头计算模型的有限元网格全部采用四面体二次单元（C3D10M），网格尺寸0.9mm，在孔边处局部加密至0.5mm，网格剖分如图12所示。

模型边界条件按照试验真实条件施加，如图13所示，夹具上部施加位移边界条件，夹具下部固支约束，试验件与夹具连接处设置接触。

图12 典型接头网格示意图

图13 含工装有限元模型边界条件示意图

7085铝合金典型接头数值计算结果的支反力随拉伸位移变化曲线见图11虚线。计算结果可知破坏载荷为52.93kN，与试验对比结果见表5，平均误差为4.7%。

表5 7085铝合金典型接头破坏载荷试验与分析结果对比

接头初始破坏位置位于耳片孔边，耳片断裂后裂纹扩展路径见图14，与试验结果（见图10）吻合。

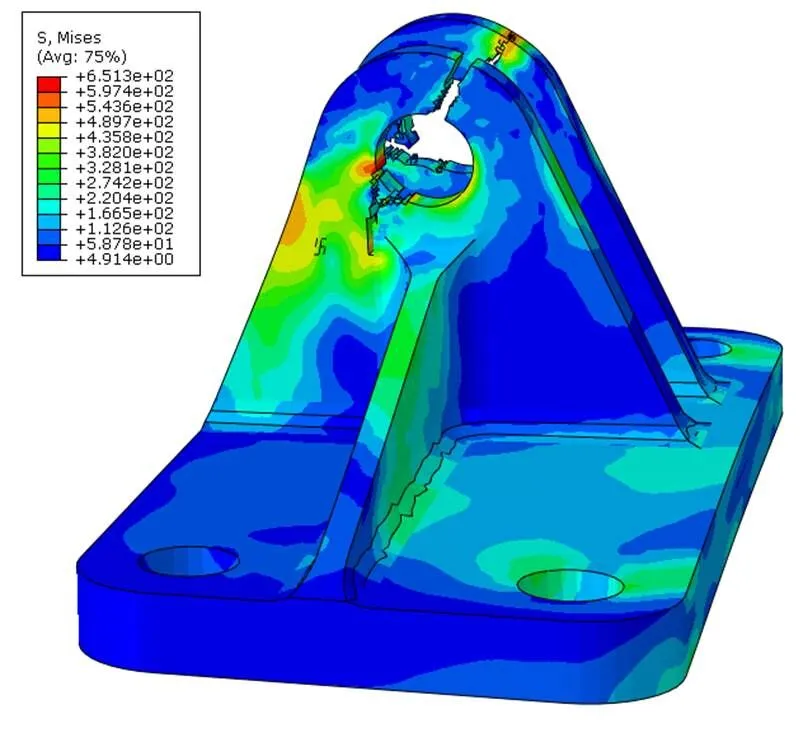
图14 铝合金典型接头破坏后裂纹扩展图

4 结论

本文通过试验与数值分析相结合的方法，对7085铝合金材料的断裂失效性能及数值预测方法进行了研究。首先，本文给出了一种研究不同应力状态下金属材料破坏性能的元件级试验方法，设计了不同规格的元件级试验件，包括圆柱压缩、平板（带角度缺口）剪切试验件以及圆棒（带缺口）拉伸，研究了7085铝合金材料在不同应力三轴度范围下的破坏性能。然后，结合有限元分析，获得了7085铝合金材料应力三轴度与断裂塑性应变的数据。通过数据拟合发现，7085铝合金材料的断裂失效基本符合失效模型的规律，以此作为该材料的延性断裂准则。最后，应用该模型对典型接头试验件进行破坏试验与数值分析对比研究，结果表明利用本文获取的材料破坏准则能够很好地预测接头破坏形式（裂纹起始点、裂纹扩展路径）以及极限承载能力。

[1] Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]. Proceedings of the 7th International Symposium on Ballistics. 1983, 21: 541-547.

[2] Wilkins ML, Streit RD, Reaugh JE. Cumulative-strain-damage model of ductile fracture: simulation and prediction of engineering fracture tests[R]. Technical Report UCRL-53058, Lawrence Livermore National Laboratory; 1980:8.

[3] Wierzbicki T, Bao Y, Lee Y W, et al. Calibration and evaluation of seven fracture models[J]. International Journal of Mechanical Sciences, 2005, 47(4/5): 719-743.

[4] Bai Y, Wierzbicki T. A comparative study of three groups of ductile fracture loci in the 3D space[J]. Engineering Fracture Mechanics, 2015, 135:147-167.

[5] Xue L, Damage accumulation and fracture initiation in uncracked ductile solids subject to triaxial loading [J]. International Journal of Solids and Structures, 2007,44: 5163-5181

[6] Liu Y J, Sun Q, et al. A stress-invariant based multi-parameters ductile progressive fracture model [J]. Materials Science and Engineering A, 2013, 576(4): 337-345.

[7] Liu Y J, Sun Q. A dynamic ductile fracture model on the effects of pressure, Lode angle and strain rate[J]. Materials Science and Engineering A, 2014, 589(2): 262-270.

[8] 谢伟, 齐紫玉, 吴建国. 复杂应力状态下30CrMnSiA材料低周疲劳性能试验研究[J]. 强度与环境, 2019,46(6):51-58. [Xie Wei, Qi Ziyu, Wu Jianguo. Experimental study on low-cycle fatigue of 30CrMnSiA high strength steel under multiaxial stress states[J]. Structure & Environment Engineering, 2019, 46(6): 51-58.]

[9] 陈爱国, 王开明, 邢佶慧, 等. 单调荷载下Q345钢焊缝金属的延性断裂性能研究[J]. 工程力学, 2020, 37(1):96-105.[Chen Aiguo, Wang Kaiming, Xing Jihui, et al. Ductile fracture behavior of weld metal for Q345 steel under monotonic loading[J]. Engineering Mechanics, 2020, 37(1): 96-105.]

[10] 刘亚宁. 基于微观机理的钢材及焊缝金属延性断裂研究[D]. 北京交通大学, 2018.

[11] 李非凡, 雷丽萍, 方刚. 镁合金塑性变形及延性断裂预测研究进展(下)—延性断裂模型的开发及应用[J]. 塑性工程学报, 2020, 27 (2):7-18.[Li Feifan, Lei Liping, Fang Gang. Research advances of plastic deformation and ductile fracture prediction of magnesium alloys. Part Ⅱ: Development and application of ductile fracture models[J]. Journal of Plasticity Engineering, 2020, 27 (2): 7-18.]

[12] 姜薇, 李亚智, 苏杰, 等. 2024-T3铝合金拉伸及剪切断裂行为[J]. 固体火箭技术, 2015(3): 426-432. [Jiang Wei, Li Yazhi, Su Jie, et al. Tensile and shear failure mechanisms of 2024-T3 aluminum alloy[J]. Journal of Solid Rocket Technology, 2015(3): 426-432.]

[13] 于思淼, 蔡力勋, 姚迪,等. 准静态条件下金属材料的临界断裂准则研究[J]. 力学学报, 2018, 50(5):1063-1080.[Yu Simiao, Cai Lixun, Yao Di, et al. The critical strength criterion of metal materials under quasi-static loading [J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(5):1063-1080.]

[14] Roth C C , Mohr D . Ductile fracture experiments with locally proportional loading histories[J]. International Journal of Plasticity, 2016: 328-354.

[15] Cao T S, Bobadilla C, Montmitonnet P, et al. A comparative study of three ductile damage approaches for fracture prediction in cold forming processes [J]. Journal of Materials Processing Tech, 2015, 216: 385-404.

Experimental and Numerical analysis of Ductile Failure of AL7085 under Complex Stress States

LIU Yan-jie GAO Xiao-qin LI Ming-qiang

（AVIC the First Aircraft Institute, Xi’an 710089, China）

In this paper, the ductile failure of AL7085 under complex stress state is researched by coupon experiment and numerical analysis in the frame of damage mechanics and ductile fracture theory. By the combination of experiment and FEM simulation, the relation of triaxiality-fracture strain is built as fracture criterion. In order to verify the accuracy of fracture criterion of AL7085, experiment of joint structure is conducted as well as the fracture simulation. The comparison of experiment and simulation shows that the fracture criterion established by coupons under complex stress state can describe the failure of joint structure in a good accuracy.

Complex stress state; joint structure; ductile failure; fracture criterion; FEM simulation

V216.5

A

1006-3919(2021)01-0040-07

10.19447/j.cnki.11-1773/v.2021.01.006

2020-10-14；

2020-12-04

中国飞机强度研究所创新基金（BYST⁃CKKJ⁃20⁃027）

刘彦杰（1988—），男，博士，工程师，研究方向：飞行器结构优化/计算固体力学；(710089)陕西西安市72信箱303分箱.