改进的动态差分优化网络的室内分级定位方法
2021-04-22陆雯霞
鄢 松,吴 飞,朱 海,陆雯霞
改进的动态差分优化网络的室内分级定位方法
鄢 松,吴 飞,朱 海,陆雯霞
(上海工程技术大学 电子电气工程学院,上海 201620)
针对指纹定位方法中单一指纹信息特征有限,以及在提升定位精度时,因增大指纹库造成指纹匹配复杂度增加,导致定位效率不高等问题,提出一种改进的动态差分优化网络的室内分级定位方法:离线阶段,在无线保真(WiFi)指纹中引入三轴地磁强度特征,增加定位区域的局部特征信息,并将指纹样本通过均值聚类算法(-means)进行聚类切分,形成区域指纹库,各区域指纹库分别利用改进的动态差分优化埃尔曼神经网络(IDDE-ENN)模型,训练得到每个区域的精细定位模型;在线定位阶段,根据用户的定位数据与区域指纹库的聚类中心匹配,在减少指纹搜索复杂度的同时,实现了区域级定位,然后通过该区域的定位模型对用户进行精细定位。实验结果表明,该方法在线定位阶段的平均定位误差为1.67 m,验证了该室内定位模型的有效性。
分级定位;动态差分;埃尔曼神经网络;地磁导航
0 引言
随着室外定位技术的不断发展,人们对定位服务的依赖越来越多,对基于位置服务的需求也日益增长。目前,室外定位技术已逐渐发展成熟,基本满足民用需求,但是在室内定位方面,由于定位场景的多样性、室内环境复杂性以及一些定位技术的局限性等原因,尚未形成一套统一的、稳定成熟的解决方案。
针对日常生活中不同的室内定位场景和定位需求,人们提出了不同的定位方法,其中主要包括行人航迹推算(pedestrian dead reckoning, PDR)[1-4]、超宽带(ultra wide band, UWB)[5]、射频识别(radio frequency identification, RFID)[6-7]、蓝牙[8]、无线保真(wireless fidelity, WiFi)等室内定位方法。然而,这些定位技术都存在着各种各样的问题,其中基于惯性传感器的PDR定位方法,惯性传感器的累积误差会逐渐地降低定位的精度;虽然UWB的定位精度较高,但高精度且定位时延低的UWB定位系统,价格相对较贵,并且传输距离也受限,一般多用于室内的小范围定位场景;此外,采用RFID定位和蓝牙定位方法时,均需要在定位场景中部署大量的定位标签设备,无疑增加了定位成本。由于WiFi在人们日常生活中使用广泛,布设范围也较广,因此,采用WiFi进行室内定位可有效地降低定位成本,同时其定位精度也可达到室内定位的需求。
目前在基于WiFi的室内定位方法当中,利用WiFi指纹进行定位的研究比较多,WiFi指纹定位主要分为两个阶段:1)离线指纹库采集阶段,需要对定位区域内的定位信号进行大量采集并形成指纹库;2)在线定位阶段,根据定位设备实时采集的信号,与指纹库进行匹配来获取位置信息。相关学者也提出了各自不同的WiFi指纹定位方法,文献[9-10]为采用近邻(-nearest neighbor, KNN)进行在线指纹匹配的室内定位算法,但由于KNN算法在在线定位时,需要与指纹库的所有指纹进行匹配计算,当指纹库较大时,无疑带来了较大指纹匹配复杂度,影响了在线定位效率,并且单一的指纹特征也限制着定位精度的提升。文献[11]提出一种均值聚类算法(-means clustering algorithm)与加权近邻(weighted-nearest neighbors, WKNN)相结合的室内定位方法:首先在离线阶段对指纹库进行聚类;然后在线定位时,仍需要对聚类后的指纹库进行搜索匹配,该方法虽采用了分级定位的思想,但是在线定位时,仍需要对聚类后的指纹库的所有指纹进行搜索匹配,并未有效地降低在线定位阶段的指纹匹配复杂度。文献[12]采用一种基于卷积神经元网络的室内定位算法,将无线接入点(access point,AP)指纹样本转换为灰度图像指纹样本后,再利用卷积神经网络进行训练,但未对指纹库进行有效划分,在较大区域定位时,直接使用整个指纹库训练也会在一定程度上影响定位精度。因此,目前WiFi指纹定位方法主要存在两个问题: 1)在较大区域的定位场景中,指纹库的体积往往也较大,从而使在线定位阶段进行指纹搜索匹配的复杂度增加,降低了在线定位效率;2)当增大指纹采集密度时,相邻指纹采集间隔较小,从而导致单一的WiFi指纹特征相似度较高,影响定位精度。
此外,在基于差分进化算法的室内定位研究中,文献[13]提出一种基于差分进化算法的指纹库定位方法,利用差分进化算法对AP的放置位置进行优化,以得到较好的指纹信息,但是也并未考虑WiFi指纹库体积导致的指纹匹配复杂度及WiFi指纹特征相似问题。文献[14]提出一种混合粒子群融合差分进化算法的室内多边定位方法,利用差分进化算法对混合粒子群算法进行优化,但由于WiFi信号的多径效应带来的距离估计误差及锚点的位置测量误差,使得该种方法定位误差比指纹库匹配定位方法的误差要大很多。文献[15]提出一种利用差分进化算法结合灰狼优化(grey wolf optimizer,GWO)算法,进行优化支持向量回归(support vector regression, SVR)的射频识别(radio frequency identification, RFID)指纹定位方法,由于SVR算法一般只适合解决小样本问题,对于定位区域比较大的指纹库定位,并不能够得到很好地解决;文献[16]提出一种利用差分进化改进贝叶斯压缩感知的定位算法,由于贝叶斯模型也是在小规模的数据集上表现较好,在较大规模的指纹数据集中性能并不佳。
针对上述问题,本文提出一种改进的动态差分优化网络的室内分级定位方法,在WiFi指纹中增加指纹点属地的三轴地磁强度,有助于降低在增加指纹采集密度后的指纹相似度;又考虑在离线阶段,将定位区域所采集的指纹利用-means算法进行聚类,形成每个聚类中心所对应的区域指纹库,然后由本文所提出的改进的动态的差分进化算法优化埃尔曼(Elman)神经网络(improved dynamic differential evolution-Elman neural network, IDDE-ENN)模型,利用各区域指纹库,分别训练出每个区域的定位模型;在线阶段,首先根据定位设备所采集的WiFi和三轴地磁强度信息与聚类中心进行匹配,实现区域级定位,然后再利用该区域的定位模型实现精细定位,在提升定位精度的同时,有效地解决了随着指纹采集密度增加导致指纹库体积增大所带来的指纹搜索匹配时间复杂度增加、在线定位效率不高的问题。
1 差分进化算法
差分进化算法[17]与遗传算法、粒子群算法相似,都是一种基于群体的随机并行优化算法,利用模拟生物种群内个体的合作和竞争关系进行群体内的优化搜索,通常用于求解非线性、不可微问题,具有速度快和鲁棒性好等特点。
差分进化算法的详细步骤如下:
1)种群初始化。在解空间中随机均匀地产生个个体,组成初始种群,即:


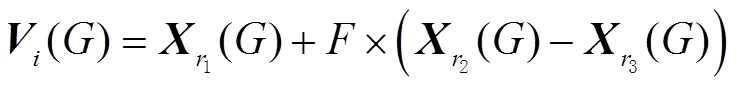
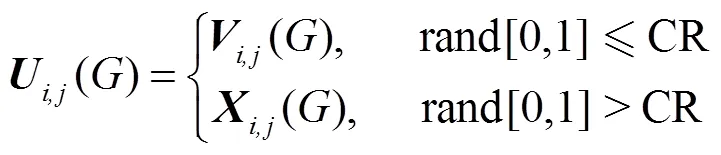

2 Elman神经网络
Elman神经网络是一种典型的动态反馈型递归神经网络[18],在反向传播(back propagation,BP)神经网络的结构基础上,在隐含层上增加一个承接层作为延时算子而达到记忆的目的,从而使该网络具有适应时变特性的能力,增强网络的全局稳定性,在计算能力、稳定性方面,Elman 神经网络比BP神经网络更优,能够快速解决寻优问题。Elman神经网络的结构主要分为四层,分别为输入层、隐藏层、承接层和输出层,其网络结构如图1所示。

图1 Elman神经网络结构
1)输入层。信号传输,将学习样本输入到网络;
2)隐含层。将输入层的输出和网络中与隐含层相连接的承接层的输出,一起作为隐含层的输入,其表达式为

3)承接层。主要用来存储隐含层各单元前一时刻的输出,可以看作一个时延算子,其表达式为

4)输出层。为隐含层单元的加权输出,其表达式为
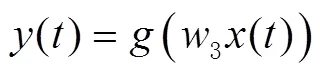
3 改进的动态差分优化网络的室内分级定位方法
3.1 基于改进差分进化算法融合Elman神经网络
由于Elman神经网络与BP神经网络类似,都是采用梯度下降法进行网络优化,容易出现训练速度慢以及局部最优解的缺陷,对该网络的训练较难达到全局最优。而差分进化算法,具有快速寻优、擅长解决多变量的非线性函数优化问题等特点,因此,考虑采用差分进化算法对Elman神经网络进行优化,但现有的差分进化算法对算法后期,随着种群个体差异减小会陷入局部最优问题的解决效果不佳,因此,本文首先提出一种改进的动态的差分进化(improved dynamic differential evolution,IDDE)算法,对差分进化算法中的缩放因子和交叉概率因子CR进行动态改进,然后将改进的差分进化算法与Elman神经网络融合进行优化,提出一种IDDE-ENN算法,这样可以有效地克服Elman神经网络的收敛速度慢和局部最优问题,IDDE-ENN算法原理如图2所示。
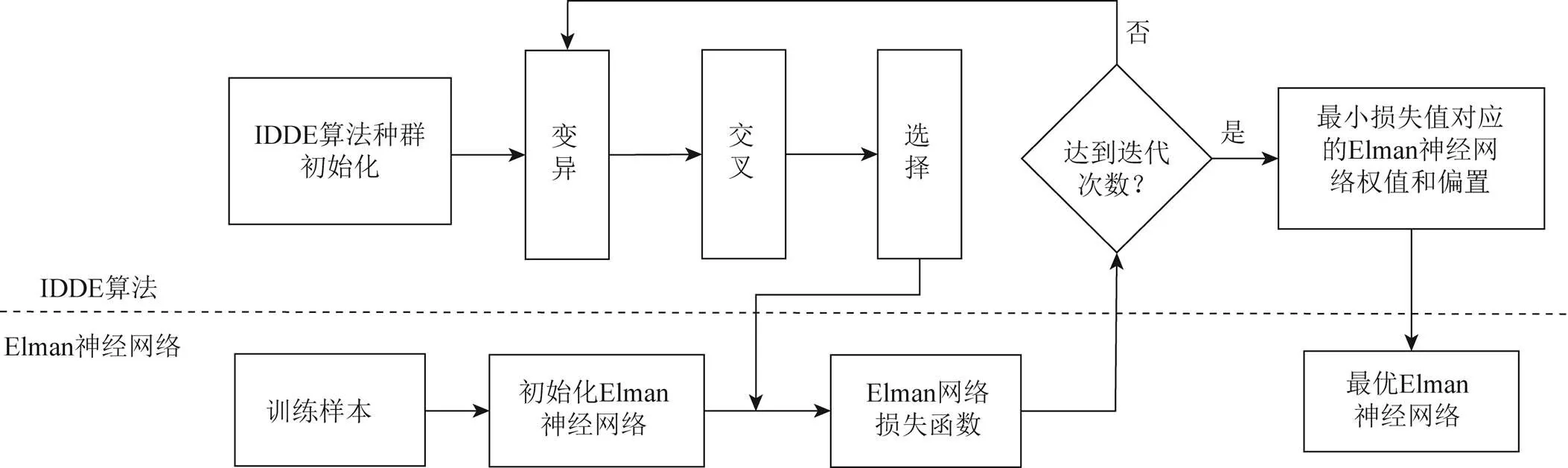
图2 本文IDDE-ENN算法原理
3.1.1 改进的动态差分进化算法优化原理
针对现有的差分进化算法并没有很好地解决算法后期随着种群个体差异的减小,算法收敛速度会变慢,容易陷入局部最优问题。本文提出一种IDDE算法,具体改进原理为:
1)对差分进化算法中的缩放因子进行改进。由差分进化算法原理可知,缩放因子的特性是:当较大时,种群能够以较快速度进行更新迭代;较小时,收敛速度也会变慢。因此,相较于固定的,本文的IDDE算法是使缩放因子能够跟随迭代次数进行动态更新,即在迭代前期,由于种群差异较大,可使较大,从而以较快速度进行迭代;而在种群个体迭代后期,随着迭代次数增加,种群个体差异减小逐渐趋于最优个体,因此使缩放因子根据迭代次数也逐渐减小,从而使种群能够在较小的范围内寻找到最优个体。
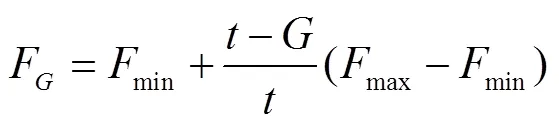
然后,由动态更新的缩放因子进行个体变异,即

2)对交叉过程中的交叉概率因子进行改进。在种群交叉过程中,将Elman神经网络的损失函数作为自适应度函数,即由自适应度函数得到的自适应度值越大,其损失函数值也越大。由式(4)可知,当交叉概率因子CR较大时,实验个体能够保留变异个体中更多的元素,当CR较小时,则会淘汰变异个体中的大部分元素。因此,合理地对CR进行取值,能够使算法达到更优效果。本文提出的IDDE算法为:首先在种群中随机选择三个个体,由自适应度函数得到每个个体的自适应度值后,由小到大进行排序;然后根据变异个体的自适应度值与随机选择的个体中的最大自适应度值之间的差值来动态更新CR,从而使CR能够根据当前迭代过程中变异个体的优劣来进行动态更新,从而使得在交叉过程中得到的实验个体也更优。具体改进原理为:
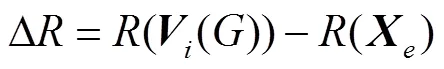
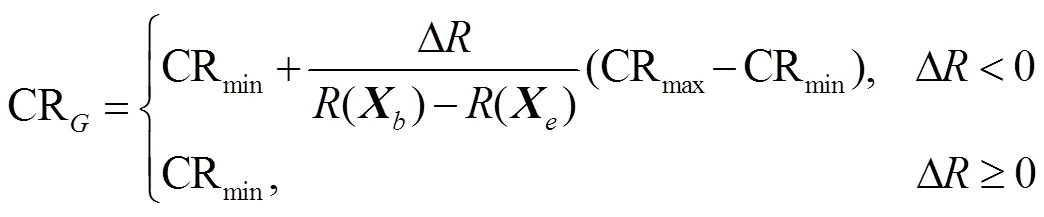
进行交叉后为
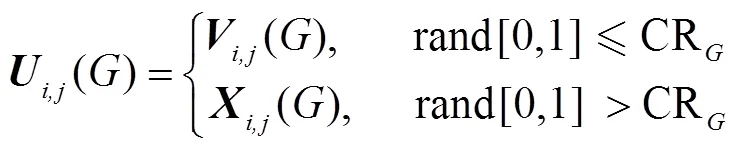
3.1.2 本文IDDE算法对Elman神经网络进行优化
针对Elman神经网络采用梯度下降法进行训练时,易出现收敛慢、局部最优解的缺陷,本文将提出的IDDE算法与Elman神经网络进行融合优化,将Elman神经网络的权值和偏置作为IDDE算法种群个体,将Elman神经网络的损失函数作为IDDE算法选择过程中的自适度函数,从而改善Elman神经网络在训练过程中陷入局部最优的缺陷,以达到最优解,实现对Elman神经网络的优化。
本文提出的IDDE-ENN算法的具体步骤如下:
1)计算Elman神经网络的损失函数,即均方根误差函数,并将其作为IDDE算法的自适应度函数,在时刻,Elman网络的隐含层输出为
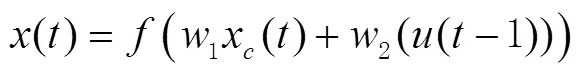
则得在时刻,其输出层的输出为
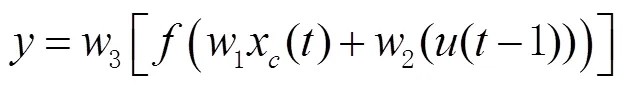

式中为Sigmoid函数。
因此可得Elman神经网络的损失函数RMSE(,),将其作为IDDE-ENN模型的自适应度函数,即

2)种群初始化。在解空间中随机均匀地产生个个体,组成初始种群,即:

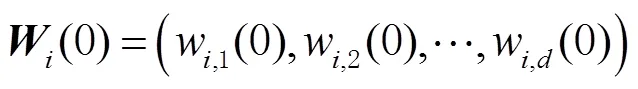
然后进行变异,即
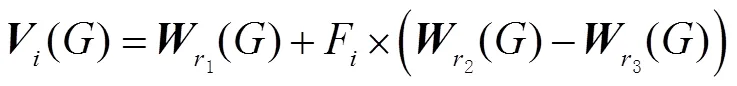


进行交叉后为
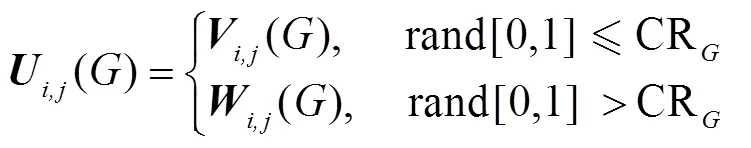

3.2 基于IDDE-ENN算法的室内分级定位方法
本文基于IDDE-ENN算法,提出一种改进的动态差分优化网络的室内分级定位方法,该定位方法主要分为两个阶段,离线阶段和在线阶段。
1)离线阶段。在离线阶段主要分为两部分:一是构建区域指纹库,首先实验人员利用采集设备,在定位区域内采集每个指纹点的WiFi和三轴地磁场强度的样本数据,然后利用基于密度聚类的-means算法,对采集的样本进行聚类,再将聚类后得到的每个类的聚类中心与该类数据做映射,形成每个区域指纹库;二是进行区域定位模型训练,将聚类形成的每个区域指纹库分别利用本文提出的IDDE-ENN模型进行训练,得到每个对应区域的室内定位模型。
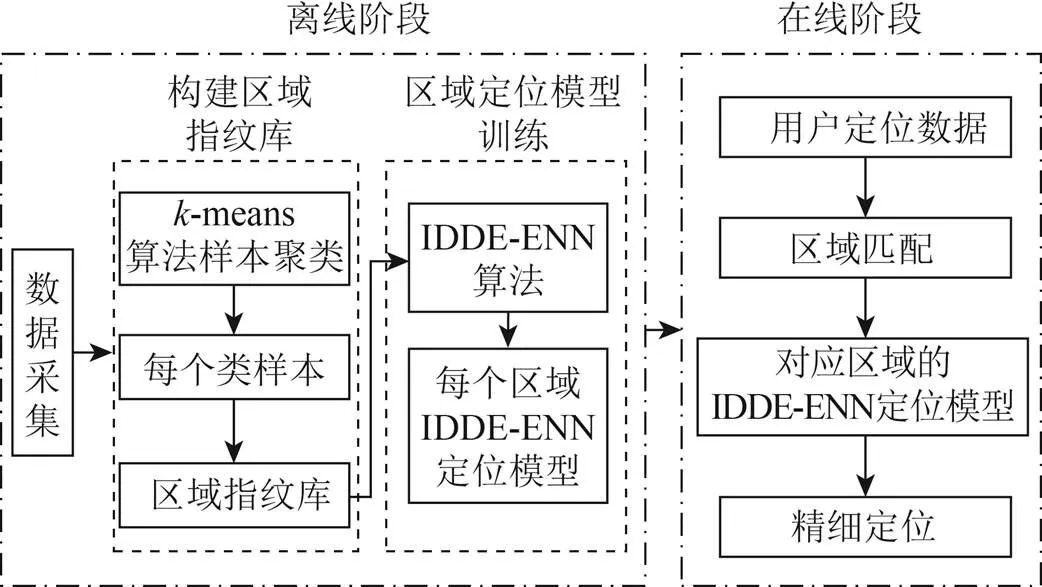
图3 改进的动态差分优化网络的室内分级定位方法
2)在线阶段。首先根据定位区域内用户设备实时采集到的WiFi和三轴地磁强度数据,与每个区域指纹库对应的聚类中心,利用欧氏距离进行搜索匹配,找到最相近的聚类中心,实现区域级定位,然后利用该区域的IDDE-ENN室内定位模型,再进行精细定位。
4 实验与结果分析
4.1 实验环境与数据采集
为验证本文提出的改进的动态差分优化网络的室内分级定位方法的定位性能,本文选取了学校实训楼二楼中的走廊和空旷的大厅区域作为实验场地,指纹点采集面积约为411 m2,在场地中使用7个实验AP,实验场地中采集数据示意图如图4所示,为便于数据采集,将实验场地分成1 m×1 m的网格。对指纹采集过程中未收集到的AP,则将其接收信号强度赋值为-100 dB·m。
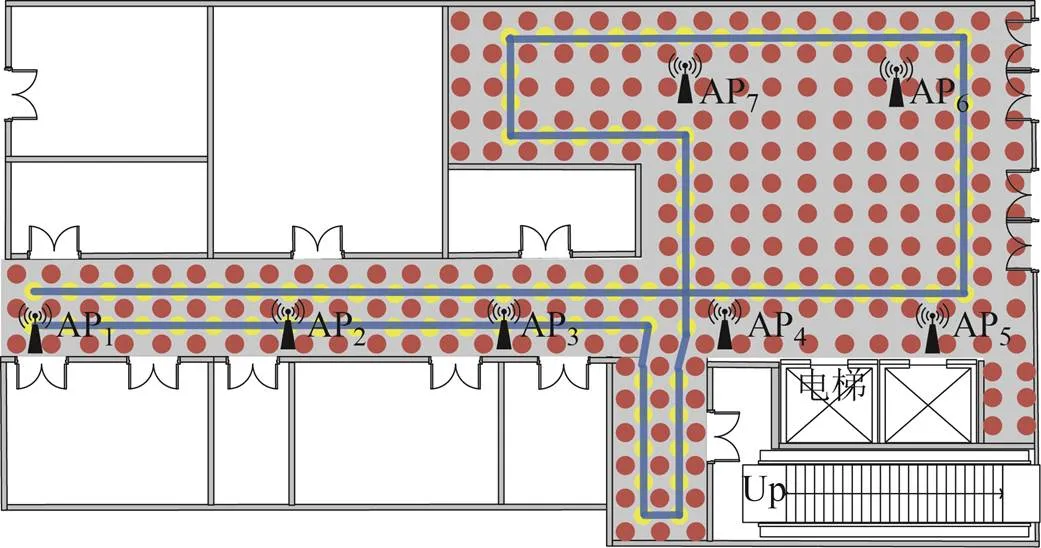
图4 实验场地中采集数据示意图
1)指纹库数据采集。采集设备为荣耀magic2手机,在每个划分的网格的中心,以2 Hz的频率采集WiFi和地磁数据的采集,分别在每个网格中心的东、南、西、北四个方向上采集20 s,即每个网格的采集总时长为80 s,共采集指纹点415个,指纹数目共66400条。
2)测试指纹数据集采集。在试验场地中设计一条测试数据集的采集路径,如图4中的蓝色线所示,蓝色路径上的黄色点为测试指纹数据采集点,实验人员手持手机采集设备,在每个采集点进行测试数据采集,每个采集点的间隔为1 m,在每个网格中心的东、南、西、北四个方向上分别采集20 s,共采集测试指纹点170个,采集的测试指纹数目共为27200条。
4.2 本文方法性能分析
1)每个区域的IDDE-ENN定位模型性能分析。在模型离线训练阶段,首先根据在实验场地中所采集的每个指纹点的WiFi和三轴地磁强度数据,利用-means算法进行样本聚类,以欧氏距离作为相似性度量。根据聚类的实验结果,当聚类算法中的参数=6时,定位性能最佳,然后将每个类的样本数据作为每个聚类中心所映射的区域指纹库。根据聚类得到每个区域指纹库,按照7:3的比例进行划分,分别得到每个区域定位模型的训练数据集和测试数据集,由每个区域的训练数据集分别进行训练,得到每个区域的IDDE-ENN定位模型。通过指纹聚类,将整个定位区域内的指纹样本聚为6个类,分别对应区域1至区域6的区域指纹库,每个区域的定位模型性能如表1所示。

表1 每个区域定位模型性能分析
每个区域定位模型的定位误差的累积分布函数(cumulative distribution function, CDF)如图5所示。由表1分析可知,除区域5和区域6以外,其他区域的平均定位误差在2 m以下。

图5 每个区域定位模型的定位误差CDF
由图5可知,当CDF不小于70%时,区域1至区域6的定位误差在2 m以内。
2)采用WiFi指纹与WiFi/地磁指纹,对整个定位模型性能进行对比分析。为了分析三轴地磁强度与WiFi指纹结合有助于增强定位指纹特征,从而减小随着指纹采集密度增加而导致的较大的指纹相似度,首先采用WiFi的指纹样本、WiFi和三轴地磁强度融合的指纹样本,分别进行训练得到各自的IDDE-ENN模型,然后分别利用4.1节中的测试指纹数据集进行对比测试分析,WiFi与WiFi/地磁的指纹定位性能对比如表2所示,定位误差的CDF对比如图6所示。

表2 WiFi与WiFi+地磁的指纹定位性能对比 单位:m

图6 WiFi指纹与WiFi+地磁指纹定位误差CDF对比
通过表2对比可看出,只有WiFi数据训练得到的定位模型,其平均定位误差为2.04 m,而WiFi融合三轴地磁强度信息的指纹样本,训练得到的定位模型的定位误差为1.67 m,平均定位误差相比降低了18.1%。由图6可知,当CDF为80%时,WiFi融合三轴地磁强度的指纹样本训练模型的定位误差为1.96 m,而WiFi样本训练的模型定位误差为2.34 m,相比较于只有WiFi特征的指纹样本训练得到的室内定位模型,WiFi与地磁特征融合的指纹样本对单独的WiFi指纹有一定的改善效果,从而使得定位模型的性能得到了一程度的提升。
3)与其它定位算法对比分析。将本文将提出的改进的动态差分优化网络的室内分级定位方法与基于其它算法的室内定位模型,分别进行了采用分级方法的定位实验和未采用分级方法的定位实验做对比分析。未采用分级方法时,各定位算法的定位性能对比如表3所示,各算法的CDF对比结果如图7所示。

表3 未采用分级方法时本文IDDE-ENN模型与其它定位方法性能对比 单位:m
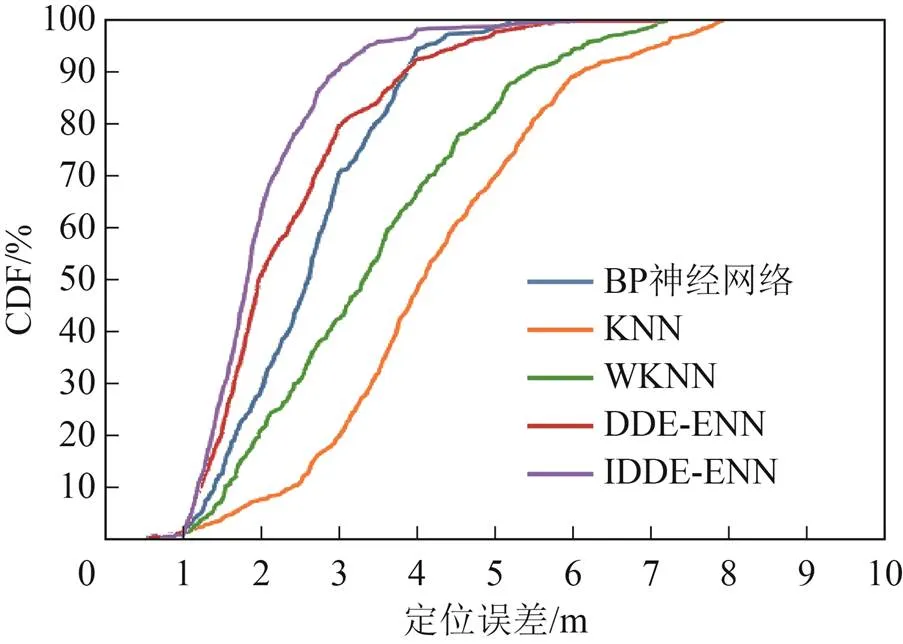
图7 未采用分级时各定位算法的定位误差CDF对比
由表3可知,当未采用分级方法时,本文IDDE-ENN定位模型的平均定位误差为2.01 m,小于未改进的动态差分进化算法优化Elman神经网络(dynamic differential evolution-Elman neural network, DDE-ENN)的定位模型的平均定位误差,采用BP模型的平均定位误差为2.63 m,基于WKNN算法的定位模型的平均定位误差在3 m以上,而KNN算法定位模型在=5达到最优定位效果时,其平均定位误差则为4.24 m。由图7可知,在未使用分级情况下的IDDE-ENN定位模型,在3 m以内定位误差的CDF达到90%,优于DDE-ENN和BP模型、以及基于KNN、WKNN算法的定位模型,因此,本文所提出的IDDE-ENN定位模型相比于基于DDE-ENN、BP、KNN以及WKNN算法的室内定位模型,在定位性能上有一定的提升效果。
采用分级方法时,首先将本文中利用-means算法聚类好的区域指纹库分别与基于DDE-ENN、BP神经网络、KNN、WKNN算法结合作为分级定位定位模型,然后与本文的IDDE-ENN分级定位模型进行对比试验,各定位模型的定位性能对比如表4所示,不同CDF定位误差对比如图8所示。

表4 采用分级方法时本文IDDE-ENN模型与其它定位方法性能对比 单位:m

图8 采用分级方法时各定位算法的定位误差CDF对比
当参数=4时,使用分级方法后的KNN算法模型定位误差最小。由表4可知,在使用分级方法时,本文IDDE-ENN模型的平均定位误差为1.67 m,而基于DDE-ENN、BP、KNN、WKNN的模型的平均定位误差均在2 m以上。由图8可知,定位误差CDF为80%时,IDDE-ENN模型的定位误差为1.96 m,而基于BP、KNN以及WKNN的定位模型的定位误差均在3 m以上。与未采用分级方法时的IDDE-ENN模型相比,采用分级后的IDDE-ENN模型,其定位误差相对降低16.9%,与采用分级后的DDE-ENN模型相比,其定位误差降低17.3%。因此,通过对比分析可知,分级定位的方法对本文的提出的IDDE-ENN定位模型的定位精度也具有一定的提升效果。
4)与其它定位方法的指纹库以及指纹匹配复杂度对比分析。为说明本文提出的IDDE-ENN定位模型在提高定位精度的同时,也降低了在线定位阶段指纹匹配的复杂度,将本文IDDE-ENN模型与其它定位方法所使用的指纹库容量、指纹匹配时间复杂度以及模型训练时长这三个方面进行对比,其对比结果如表5所示。

表5 各方法的指纹库以及在线定位指纹匹配的复杂度对比分析
为便于分析,设指纹点总数为个,KNN和WKNN算法是取每个指纹点每个采集方向上的指纹强度的均值作为一条指纹,则可得KNN和WKNN所使用的指纹数量为4,而BP、DDE-ENN和IDDE-ENN算法的指纹数量则为160;采用常采用衡量算法时间复杂度的大O符号表示法,对各定位算法的指纹匹配复杂度进行对比分析,设利用-means聚类算法将指纹库分为个区域指纹库,由于在使用KNN和WKNN算法时,不管将指纹库分为多少个类,在线定位时其总是需要遍历所有指纹库才能找到最相近的个指纹,因此可得KNN和WKNN定位算法的在线定位指纹匹配的复杂度为O(4),而BP、ENN和IDDE-ENN算法则只需要与个聚类中心进行比较即可,所以BP、DDE-ENN和IDDE-ENN算法的在线定位指纹匹配复杂度为O(),其中远小于4,指纹匹配复杂度相对更低;在模型训练时长方面,KNN和WKNN算法不需要进行训练,由表5可知,IDDE-ENN模型训练时长与BP和DDE-ENN网络相比,也较长。通过对采用分级方法时,各定位方法的平均定位误差对比可知,虽然IDDE-ENN模型的所使用的指纹库较大,离线阶段训练时长也较大,但由于IDDE-ENN模型的定位误差更小,且在线定位时指纹匹配复杂度也相对较低,在模型训练完后,在线定位时只需加载训练好的模型即可,所以IDDE-ENN模型相对更优。
5 结束语
为了提高室内定位的精度并降低指纹库匹配的复杂度,本文提出一种改进的动态差分优化网络的室内分级定位方法,首先通过聚类算法将定位区域内、包含WiFi和三轴地磁强度的指纹样本进行聚类,然后根据聚类中心,将每个类样本作为区域指纹库,再将每个区域指纹库分别利用本文提出的IDDE-ENN模型进行训练,生成区域定位模型。在线定位阶段,首先利用用户设备采集的WiFi和三轴地磁强度数据,根据欧氏距离找到最相近的聚类中心进行区域定位,然后通过该聚类中心对应的区域定位模型实现精细定位。通过实际环境试验,本文提出的室内分级定位算法的平均定位误差为1.67 m,在提升定位精度的同时也降低了指纹匹配复杂度,证明了本文所提出的定位方法的有效性。
[1]FAN Q G, ZHANG H, PAN P, et al. Improved pedestrian dead reckoning based on a robust adaptive Kalman filter for indoor inertial location system[J]. Sensors, 2019, 19(2): 294-315.
[2]YU J G, NA Z Y, LIU X, et al. WiFi/PDR-integrated indoor localization using unconstrained smartphones[J]. EURASIP Journal on Wireless Communications and Networking, 2019(1): 1-13.
[3]石柯, 宋小妹, 王信达, 等. 多传感器辅助的WiFi信号指纹室内定位技术[J]. 软件学报, 2019, 30(11): 3457-3468.
[4]宋世铭, 王继, 韩李涛. 一种基于改进粒子滤波算法的室内融合定位方法[J]. 导航定位学报, 2020, 8(1): 99-106.
[5]张宝军, 田奇, 王珩, 等. 基于CNN和在线学习的UWB室内定位算法[J]. 传感技术学报, 2020, 33(4): 511-516.
[6]李丽, 郑嘉利, 王哲, 等. 基于异步优势动作评价的RFID室内定位算法[J]. 计算机科学, 2020, 47(2): 233-238.
[7]邓昀, 朱彦, 杨逸夫, 等. 基于BP神经网络的RFID室内定位算法研究[J]. 小型微型计算机系统, 2019, 40(8): 1707-1712.
[8]武涛. 基于WiFi和蓝牙融合的室内定位算法的研究[D]. 芜湖: 安徽工程大学, 2019.
[9]羊宗灏, 程凯, 周宝定, 等. 基于RSS相关性的位置指纹室内定位方法[J]. 智能计算机与应用, 2017, 7(2): 8-13.
[10]吴泽泰, 蔡仁钦, 徐书燕, 等. 基于K近邻法的WiFi定位研究与改进[J]. 计算机工程, 2017, 43(3): 289-293.
[11]王亚涛, 王新珩, 董育宁, 等. 基于Kmeans和动态WKNN的两层Wi-Fi改进定位方法[J]. 南京邮电大学学报(自然科学版), 2017, 37(5): 41-47.
[12]李志, 赵大哲. 一种基于卷积神经元网络的室内定位算法[J]. 小型微型计算机系统, 2019, 40(3): 533-537.
[13]LIU J L, XU B G, WAN Y H, et al. A rang-free location method based on differential evolution algorithm[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Cross Strait Quad-regional Radio Science & Wireless Technology Conference. Chengdu: IEEE, 2013: 381-384[2020-05-28].
[14]吴斌, 金洁丽. 混合粒子群和差分进化的定位算法[J]. 通信技术, 2020, 53(4): 873-879.
[15]徐杨杰, 王艳, 严大虎, 等. 基于Newton插值与混合灰狼优化SVR的RFID定位算法[J]. 系统仿真学报, 2017, 29(9): 1921-1929.
[16]李文浩. 矩阵填充结合贝叶斯压缩感知的位置指纹定位[D]. 沈阳: 辽宁大学, 2016.
[17]STORN R, PRICE K. Differential evolution - a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.
[18]ELMAN J L. Finding structure in time[J]. Cognitive Science, 1990, 14(2): 179-211.
Indoor hierarchical positioning based on dynamic differential optimization network
YAN Song, WU Fei, ZHU Hai, LU Wenxia
(School of Electronic and Electrical Engineering, Shanghai University of Engineering Science, Shanghai 201620, China)
Aiming at the problems of limited single fingerprint information features in fingerprint positioning methods, and high fingerprint matching complexity and low positioning efficiency due to the increase of fingerprint database when improving positioning accuracy, the paper proposed an indoor hierarchical positioning method based on dynamic differential optimization network: at the offline stage, three-axis geomagnetic features were introduced into Wireless Fidelity (WiFi) fingerprints to increase the local feature information of the positioning area, and the fingerprint samples were clustered and segmented to form a regional fingerprint database by the-means algorithm, then the fingerprint database of each region was trained to obtain a fine positioning model for each region by using the Improved Dynamic Differential Evolution-Elman Neural Network (IDDE-ENN) algorithm; at the online positioning stage, the location data of the user were matched with the cluster center of the regional fingerprint database, and the region-level positioning was achieved with reducing the complexity of fingerprint searching, then the user was finely positioned through the regional positioning model. Experimental result showed that at the online positioning stage, the average positioning error of the proposed method would be 1.67 m, indicating the validity of the indoor positioning model.
hierarchical positioning; dynamic difference; Elman neural network; geomagnetism navigation
P228
A
2095-4999(2021)02-0012-09
鄢松,吴飞,朱海,等.改进的动态差分优化网络的室内分级定位方法[J].导航定位学报, 2021, 9(2): 12-20.(YAN Song, WU Fei, ZHU Hai,et al. Indoor hierarchical positioning based on dynamic differential optimization network[J].Journal of Navigation and Positioning, 2021, 9(2): 12-20.)
10.16547/j.cnki.10-1096.20210203.
2020-06-19
国家自然科学基金青年科学基金项目(61902237);上海市“科技创新行动计划”高新技术领域项目(18511101600);上海市科委青年科技英才“扬帆计划”项目(19YF1418200)。
鄢松(1993—),男,河南信阳人,硕士研究生,研究方向为室内定位。
吴飞(1968—),男,上海人,博士,教授,研究方向为计算机并行处理与节能控制,信息物理融合系统,室内定位技术等。
