基于基线解算精度的GNSS多系统组合平差权比模式分析
2021-04-22陈正宇崔浩猛朱号东赵祥伟
陈正宇,崔浩猛,朱号东,赵祥伟
基于基线解算精度的GNSS多系统组合平差权比模式分析
陈正宇1,崔浩猛2,朱号东1,赵祥伟1
(1. 中国能源建设集团江苏省电力设计院有限公司,南京 211102;2. 武汉大学 测绘学院,武汉 430079)
为确定全球卫星导航系统(GNSS)加权组合解算中可行的定权方式,提高多系统组合定位精度,选用澳大利亚多卫星系统实验(MEGX)网中,15个均匀分布的跟踪站、2019年1月的实测数据,对4个GNSS单系统进行基线解算和网平差,在评定和对比各单系统独立解算结果后,提出利用单日解基线的标准化均方根(NRMS)的三种定权模式进行定权,分析比较这三种定权模式和等权定权模式,在双系统和四系统组合网平差中对定位结果的影响。计算结果表明,全球定位系统(GPS)基线解的NRMS平均值为0.168,北斗卫星导航系统(BDS)次之,为0.186,格洛纳斯卫星导航系统(GLONASS)最低,为0.227;在这四种定权模式下,GPS 与其它GNSS系统组成的双GNSS系统加权组合平差的结果,同四GNSS系统加权组合平差的结果比较接近,各测站水平方向的平均绝对误差小于0.5 cm,高程方向的平均绝对误差均在1 cm以内;以单日解NRMS平方值定权模式,相比于等权、以单日解NRMS定权、和以平均NRMS定权三种模式,据有更高的解算精度,且相比于BDS、伽利略卫星导航系统(Galileo)、GLONASS 单系统平差的结果有明显的提升,与GPS 单系统在水平方向的平差结果较为接近,但在高程方向要优于GPS 单系统的解算精度。
全球卫星导航系统;基线解算;标准化均方根误差;定权模式;组合平差
0 引言
随着美国的全球定位系统(global positioning system, GPS)、俄罗斯的格洛纳斯卫星导航系统(global orbiting navigation satellite system, GLONASS)、欧盟的伽利略卫星导航系统(Galileo satellite navigation system, Galileo)及中国的北斗卫星导航系统(BeiDou navigation satellite system, BDS)的现代化建设及各国卫星导航定位技术的蓬勃发展,国内外越来越多的高精度卫星解算软件,具备了处理全球卫星导航系统(global navigation satellite system, GNSS)多系统数据的能力[1-3];其中,由美国麻省理工学院(Massachusetts Institute of Technology, MIT)与美国斯克里普斯海洋研究所(Scripps Institution of Oceanography, SIO)共同研制的高精度数据后处理软件加米特(GAMIT)/格洛布克(GLOBK),从10.61 版本开始,逐步实现了对包含GPS、BDS、Galileo、GLONASS在内的多系统观测数据的解算功能[4-5]。很多学者对此也展开了相关的研究分析:文献[6]选取了卫星截止高度角、天顶对流层延迟和测站约束值三个控制参数,对BDS长基线解算精度进行响应测试;文献[7]从可见卫星数、分布及其空间结构等方面,对比分析了BDS和GPS的基线解算质量差异;文献[8]利用GAMIT软件进行GPS和BDS的基线解算,其结果显示GPS和BDS单时段基线解的标准化均方根(normalized root mean square, NRMS)满足高精度基线解算要求,且GPS基线解算在、、三个方向上的精度优于BDS;文献[9]着重分析GAMIT在BDS长、短基线解算方面的精度差异,结果表明,相对于GPS,BDS短基线的解算结果,各向分量差值优于3 mm,且BDS长基线解算的水平分量和高程分量差值分别优于6 mm和1.3 cm;文献[10]利用GLOBK软件对GPS和BDS基线分别进行了单独网平差和联合网平差,结果显示,单GPS解算结果略优于单BDS,而GPS/BDS组合解与单GPS较为吻合;文献[11]选取不同的国际GNSS服务组织(international GNSS service, IGS)站,对比分析软件GLOBK平差时测站坐标和速度的精度,结果表明,当与斯克里普斯轨道和常驻阵列中心(Scripps Orbit and Permanent Array Center, SOPAC)提供的全球解h文件一起平差时,所得到的测站坐标和速度的精度最高。考虑到对于GNSS四系统综合解算的研究仍有欠缺,本文以均匀分布在澳大利亚及其周边地区的15个多GNSS实验计划(multi-GNSS experiment, MEGX)跟踪站、在2019年1月期间的观测数据为例,分别对GPS、BDS、Galileo和GLONASS四大卫星导航系统的观测数据进行基线解算,统计其各自的NRMS和基线重复性,评估比较各系统的基线解算质量和单独网平差精度,进而基于各系统的单时段基线解算精度,重点探讨和对比不同权比模式下,GPS/BDS、GPS/Galileo和GPS/GLONASS双系统组合网平差和四系统组合网平差的定位精度,最后给出了组合平差精度最优的定权方式。
1 单系统的基线解算及网平差的结果分析
1.1 基线解算模式
本文采用了澳大利亚及周边地区的15个MEGX跟踪站的连续观测资料,测站分布如图1所示。
在基线解算前,首先利用数据格式转换、元数据编辑及数据质量检查(translation, editing and quality checking, TEQC)软件进行数据的预处理和检核,以确保数据质量。基线解算采用双差模式[12],观测方程为

图1 15个MEGX跟踪站的分布

在基线解算过程中,本文所选用卫星的高度截止角为10°,数据采样间隔为30 s,观测值模式为无电离层组合(LC auto clean, LC-AUTCLN)模式,天顶延迟改正模型选择全球气温气压(global pressure/temperature, GPT2)模型,海潮模型和固体潮模型分别采用有限元解(finite element solution,FES2004)模型和国际地球自转和参考系服务(The International Earth Rotation and Reference Systems Service, IERS03)模型。根据以上基线解算模式,分别对GNSS四系统的观测数据进行求解。
关于基线解算流程,在文献[13]中已有详细介绍,本文对此不再赘述。
1.2 四系统基线解的对比分析
基线解算精度的评价指标包括NRMS、坐标重复性和基线向量的相对重复性等[14]。其中,NRMS为单时段解算出的基线值偏离其加权平均值的程度,其计算公式为

图2绘制了四系统单日NRMS值变化曲线。

图2 四系统单天基线解的NRMS
从图2可以看出,GPS、BDS和Galileo基线解的NRMS小于0.3,满足高精度基线解算要求。其中,GPS基线解的NRMS平均值最小,为0.1683,其整体波动也最小,即最为稳定;BDS次之,NRMS平均值为0.1861,其单日NRMS略低于GPS,但明显优于另外两个系统;Galileo基线解的NRMS平均值为0.2170;而GLONASS单日解NRMS波动幅度最大,且有个别天的解不满足精度要求,剔除后,其NRMS平均值为0.2272。
提取NRMS值满足高精度要求的解算结果文件,进而计算相应的坐标重复性和基线重复性。剔除损坏基线后,首先,以基线长度为横轴,分别以四系统基线解在、、三个方向上的坐标重复性和基线向量的相对重复性为纵轴,绘制其解算结果示意图如图3、图4所示;其次,统计基线解重复性的平均值,结果如表1所示。

表1 四系统基线解的坐标重复性和基线向量的相对重复性的均值统计

图3 四系统单天基线解的坐标重复性
结合图3和表1可知,四系统在水平方向上的解算精度高于高程方向。在水平方向上,GPS坐标重复性明显小于另外三个系统,且其值小于0.01 m;BDS和Galileo在、方向的坐标重复性分别小于0.03和0.06 m,在、方向的坐标重复性的平均值分别为0.0129、0.0198 m和0.0109、0.0111 m,整体而言,Galileo基线解精度优于BDS;GLONASS基线解的坐标重复性变化范围较大,个别基线甚至超过0.1 m。在高程方向上,GPS基线解的坐标重复性小于0.02 m,BDS、Galileo和GLONASS基线解算精度相对较差,且波动较大。GPS基线向量的相对重复性基本小于5×10-9,基线解算质量较高;BDS和Galileo基线向量的相对重复性基本小于2×10-8,且平均值达到1×10-9量级;GLONASS由于个别测站(如PARK站)的观测数据质量相对较低,导致整体解算质量较低,其基线向量相对重复性的平均值为13.86×10-9,若剔除PARK站的数据,其基线向量相对重复性的平均值为5.96×10-9。
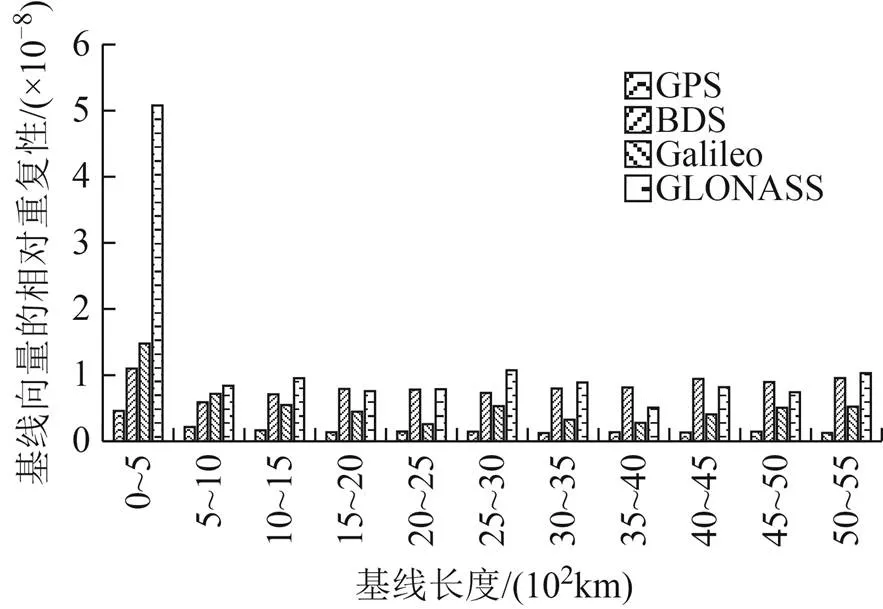
图4 四系统基线向量的相对重复性
1.3 单系统网平差结果的对比分析
对满足基线解精度要求的年积日,选择相应单天解结果文件进行单系统网平差,解算得到15个测站在各单系统下的最终坐标。以SOPAC网站发布的测站坐标作为真值,计算各测站31天的坐标误差,并由此计算15个测站坐标的绝对误差平均值(简称Ave.)和均方根误差(root mean square error, RMSE)如表2所示。

表2 单系统下15个测站的坐标误差的平均值和RMSE 单位:cm
从表2可以看出,GPS各向解算精度最高,其坐标平均绝对误差基本小于0.5 cm;BDS次之,其、方向平均绝对误差分别为0.74、2.18 cm,高程方向平均绝对误差较大,为4.91 cm;Galileo和GLONASS解算精度相对较低,在水平方向上,GLONASS略优于Galileo,但在高程方向上低于Galileo。
2 多系统加权组合网平差的结果对比分析
2.1 四种定权模式
利用多系统的基线解进行组合平差时,可以在h文件的清单列表文件(*.gdl)中,对各h文件添加不同的参数,来设置其权重因子。考虑到基线解算的质量对平差的结果有直接的影响,而NRMS作为衡量基线解算结果的一个重要指标,其值越小,基线精度越高,平差结果越理想,因此,本文以单日解NRMS值为依据,提出并对比了组合平差的四种定权模式,它们分别是:
1)等权组合平差;
2)根据单日解NRMS的比值定权,即

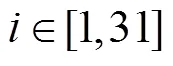
3)根据单日解NRMS平方的比值定权,即

4)根据所有参与解算的年积日的平均NRMS的比值定权,即

根据上述四种权比模式,本文将分别对GNSS双系统和四系统组合网平差结果进行精度分析。
2.2 双系统加权组合网平差
图5中给出了BDS、Galileo和GLONASS分别与GPS组合网平差的解算结果。
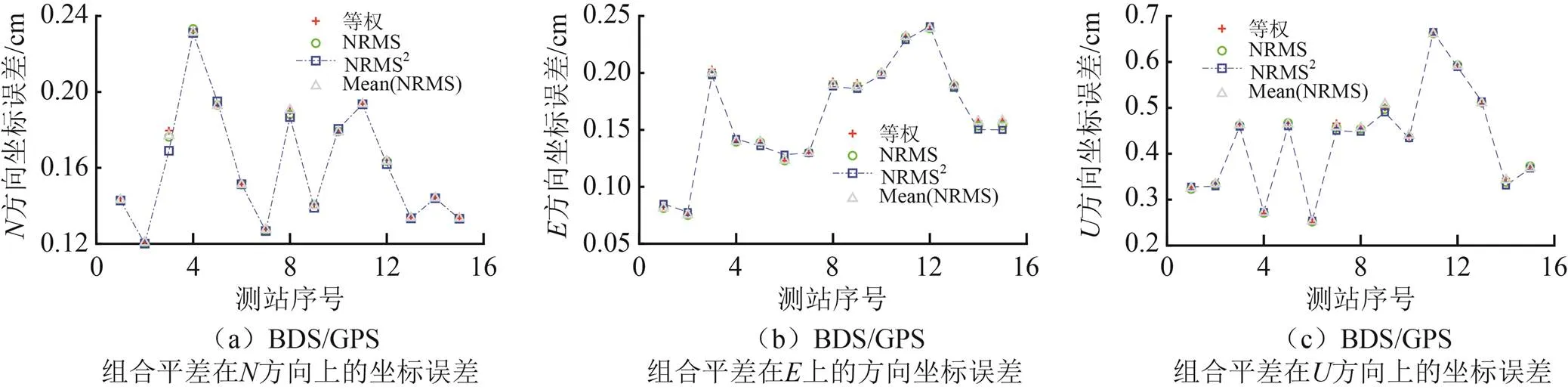
从图5可以看出,三个系统分别与GPS组合进行网平差的精度,相比于其单独网平差均有所提升,且在四种权比模式下,双系统组合平差的结果较为接近。但总体而言,根据单日解NRMS平方的比值定权的方式(模式3),解算精度更高;其中,在模式3的定权方式下,通过BDS/GPS组合平差,15个测站在、、三个方向的平均绝对误差分别为0.16、0.16和0.42 cm,相比于另外三种定权方式的结果,其坐标精度提升为0.01~0.1 mm;与BDS/GPS类似,Galileo/GPS和GLONASS/GPS采用模式3定权进行组合网平差,15个测站在三个方向上的坐标平均绝对误差分别为0.15、0.16和0.40 cm,以及0.17、0.16和0.40 cm。
为了更好地比较不同权比模式下,组合网平差与单系统网平差的精度差异,采用计算不同方向相对误差的方法进行比较,计算方法为

式中:Error为测站平均绝对误差;上标为参与平差的卫星系统,下标为坐标误差的三个方向。
由式(6)计算得到双系统组合平差相比于BDS、Galileo和GLONASS单系统平差在各向坐标精度的提升率,结果如表3所示。
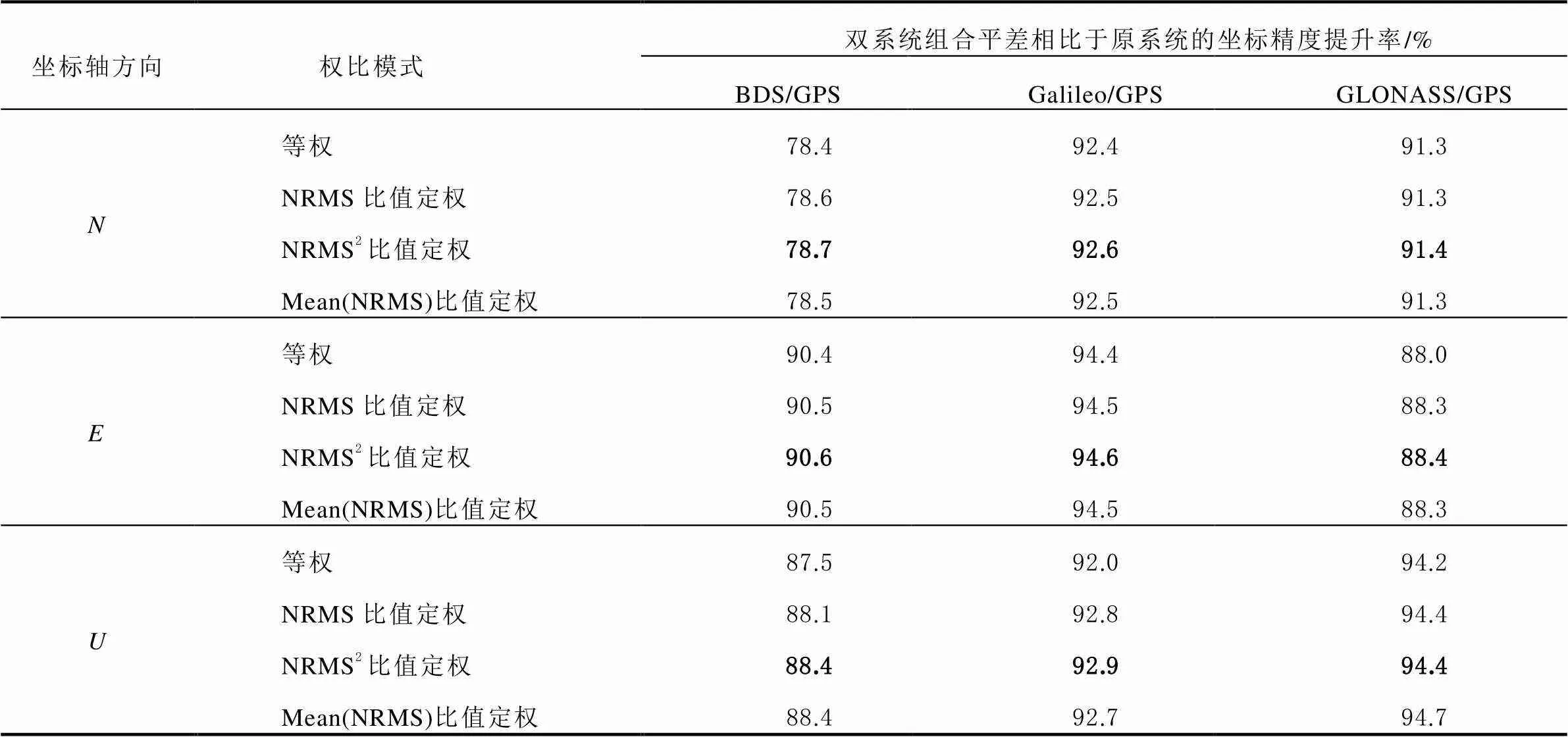
表3 不同定权模式下,双系统组合网平差的坐标精度提升率
从表3中可以看出,三种双系统组合平差的精度相比于原系统的提升在75%~95%范围为,除GLONASS/GPS的方向外,对于其余双系统组合进行网平差,采用模式3定权模式对结果精度的提升幅度最高,而以等权模式的双系统组合网平差结果相对较差。
2.3 四系统加权组合网平差
采用不同定权模式进行四系统组合网平差,其各测站的平均绝对坐标误差如图6所示。
由图6可以看出,四种权比模式下的四系统组合网平差,15个测站在水平方向的平均绝对坐标误差在2.5 mm以内,而高程方向小于6.5 mm,这与双系统组合网平差结果相近,且多数测站在模式3的定权模式下精度最高,模式2和模式4次之,等权模式下的平差精度最低。
此外,本文还统计了四种组合模式下,GNSS四系统加权组合网平差坐标的平均绝对误差,并与GPS单系统网平差的结果进行了比较,结果如表4所示。

表4 由四系统加权组合平差得到的15个测站平均绝对坐标误差 单位:cm
从表4中可以看出,相比于其它三种定权模式,采用模式3定权的四系统加权组合网平差得到15个测站在、和三个方向上的坐标绝对误差减小0.02~0.14 mm,且整体平差精度与单GPS基本一致;在水平方向上,与单GPS有0.01~0.04 mm的差距,在高程方向,定位误差比单GPS小1.14 mm。
综上所述,在四种权比模式下,四系统加权组合平差结果较为接近,但利用单日解NRMS平方的比值定权方式,相比于其他三种的结果精度更高,在水平方向上,其定位精度基本与GPS一致,但在高程方向则要优于GPS。
3 结束语
本文利用均匀分布于澳大利亚及周边地区的15个MEGX跟踪站31天的实测数据,首先进行了四系统基线解算和单系统网平差,进而基于各单日解基线NRMS值,提出了四种不同定权模式,同时对比分析双系统加权组合平差和四系统加权组合平差的结果,得到如下结论:
1)基线解算中,GPS基线解的NRMS值最小,BDS次之;从坐标重复性和基线相对重复性两方面看,BDS基线解在三个方向的坐标分量重复性平均值分别为0.0129、0.0198和0.0411 m,基线相对重复性均值为7.96×10-9,满足高精度基线解算要求。
2)单系统网平差中,BDS网平差的水平方向解算精度较高,其平均误差分别为0.74和2.18 cm,但高程方向误差较大,平均误差达到4.91 cm,整体精度略低于GPS,但优于Galileo和GLONASS。
3)四种不同权比模式下,双系统组合平差结果较为接近,但相比于原单系统的平差精度,则有明显提升,其中,采用单日解NRMS平方的比值定权方式,其解算精度最高;四系统在不同权比下的组合平差结果与双系统的类似,且以单日解NRMS平方的比值定权的解算结果要优于另外三种模式,其在水平方向解算结果与单GPS的基本一致,但在高程方向上,定位误差比GPS单系统小1.14 mm。
本文对比分析四系统基线解的质量,并提出以单日解NRMS值为依据的三种定权模式,系统地比较了GNSS双系统和四系统加权组合网平差结果精度,最终确定了GNSS多系统组合网平差的最佳定权方案,可为多系统组合精密导航定位的研究和实际应用提供参考。
[1]杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测: 试验验证数据分析[J]. 中国科学: 地球科学, 2018, 48(5): 584-594.
[2]PAN Lin, ZHANG Xiaohong, LI Xingxing, et al. Satellite availability and point positioning accuracy evaluation on a global scale for integration of GPS, GLONASS, BeiDou and Galileo[J]. Advances in Space Research, 2019, 63(9): 2696-2710.
[3]张小明. BERNESE与GAMIT的GNSS数据解算结果比较[J]. 测绘与空间地理信息, 2019, 42(7): 208-210.
[4]高志钰, 李建章, 刘彦军, 等. 利用BDS数据反演大气可降水量及其精度分析[J]. 测绘通报, 2019(5): 35-38, 47.
[5]DAI Peipei, YANG Xuhai, QIN Weijin, et al. Analysis of BDS-2+BDS-3 combination real-time time transfer based on iGMAS Station[C]//中国卫星导航学术年会组委会. 第十届中国卫星导航学术年会论文集. 北京: 中国卫星导航学术年会组委会, 2019: 1[2020-06-12].
[6]李建涛, 朱兰艳, 李永梅, 等. 基于GAMIT的不同参数对北斗长基线精度的影响分析[J]. 全球定位系统, 2018, 43(5): 23-28.
[7]于龙昊, 丁克良, 周命端, 等. 基于GAMIT-北斗的基线解算方法与实践[J]. 黑龙江工程学院学报, 2019, 33(1): 30-35.
[8]刘洋洋, 党亚民, 许长辉. 基于GAMIT对国家GNSS基准站进行的北斗基线解算分析[J]. 测绘工程, 2019, 28(3): 25-29.
[9]张双成, 王倩怡, 刘奇, 等. BDS精密相对定位精度的GAMIT分析[J]. 测绘科学, 2018, 43(12): 92-97.
[10]刘邢巍, 蒲德祥, 高翔, 等. 基于GAMIT10. 61的高精度GPS/BDS数据处理及精度对比分析[J]. 全球定位系统, 2018, 43(5): 77-83.
[11]王健, 刘宗强, 朱亚兵. 不同解算策略下的GNSS区域网平差分析[J]. 导航定位学报, 2018, 6(1): 97-102.
[12]张双成, 海洋, 李海英. 基于GAMIT的GPS长基线解类型分析及应用[J]. 工程勘察, 2011, 39(10): 42-45.
[13]赵建三, 杨创, 闻德保. 利用GAMIT进行高精度GPS基线解算的方法及精度分析[J]. 测绘通报, 2011(8): 5-8, 35.
[14]李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009.
[15]武曙光. 区域CORS站坐标时间序列特征分析[D]. 武汉: 武汉大学, 2017.
Research on weighting schemes of each GNSS in their combinatorial adjustment based on the accuracy of baseline solutions
CHEN Zhengyu1, CUI Haomeng2, ZHU Haodong1, ZHAO Xiangwei1
(1.Jiangsu Power Design Institute Co. Ltd. of China Energy Engineering Group, Nanjing 211102, China;2.School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China)
In order to determine the optimal weight ratio of each Global Navigation Satellite System (GNSS) in their combinatorial adjustment and improve the accuracy of positioning results, we firstly calculate baseline solutions of single GNSS including Global Positioning System (GPS), BeiDou navigation satellite System (BDS), Galileo navigation satellite system (Galileo) as well as GLObal Navigation Satellite System (GLONASS), and then respectively generate their each positioning results by 3D network adjustment using the measurements from 15 tracking stations evenly distributed in the Australia Multi-GNSS EXperiment (MGEX) network during the January of 2019. Furthermore, we comparatively analyzed the positioning solutions estimated by dual-system weighted combinatorial adjustment and four-GNSS weighted combinatorial adjustment, where the weighting factor of each GNSS is predetermined by four different schemes based on Normalized Root Mean Square (NRMS) of each single-day solution. The results indicate that, the average of the NRMS of BDS baseline solutions is 0.186, that of GPS is 0.168, and that of GLONASS is 0.227; the results respectively estimated by the dual-system weighted combinatorial adjustment and four-GNSS weighted combinatorial adjustment are basically consistent with each other, and specifically, the errors of coordinate component in the horizontal and vertical direction are less than 0.5 cm and 1 cm, respectively. In addition, according to the results by combinatorial adjustment with apposite weighting factor predetermined using the square of NRMS, which is better than that by other weighted combinatorial adjustment where the weighting factor of each GNSS is equal to 1 or respectively given based on NRMS-only and the average of NRMS, it can be found that the accuracy of the horizontal component is almost the same as that by GPS-only while the accuracy of the Up component is better than the latter. However, the results by the aforesaid weighted combinatorial adjustment are all better than that respectively estimated by BDS-only、Galileo-only and GLONASS-only.
global navigation satellite system; baseline solutions; normalized root mean square; weighting strategy; combinatorial adjustment
P228
A
2095-4999(2021)02-0067-08
陈正宇,崔浩猛,朱号东,等.基于基线解算精度的GNSS多系统组合平差权比策略分析[J].导航定位学报,2021,9(2): 67-74.(CHEN Zhengyu,CUI Haomeng,ZHU Haodong,et al.Research on weighting schemes of each GNSS in their combinatorial adjustment based on the accuracy of baseline solutions[J].Journal of Navigation and Positioning,2021,9(2): 67-74.)
10.16547/j.cnki.10-1096.20210211.
2020-07-15
陈正宇(1982—),男,江苏南京人,硕士,高级工程师,研究方向为GNSS在电力工程中的应用。
崔浩猛(1994—),男,河北邯郸人,博士研究生,研究方向为卫星大地测量。
