改进卡尔曼滤波的行人导航算法

钟启林，衷卫声，熊 剑，郭 杭

改进卡尔曼滤波的行人导航算法

钟启林，衷卫声，熊 剑，郭 杭

（南昌大学 信息工程学院，南昌 330031）

针对使用传统白噪声卡尔曼滤波算法实现行人导航时，存在因惯性测量单元（IMU）的有色噪声影响，而使得行人导航位置精度过低的问题，提出一种基于有色噪声改进卡尔曼滤波的行人导航算法：采用自回归模型对微机电型IMU的有色噪声进行建模；然后根据建模结果对卡尔曼滤波算法进行改进；最后构建基于改进卡尔曼滤波的行人导航算法。实验结果表明，该法相对于采用白噪声模型的行人导航算法具有更好的定位精度，定位精度可以提高24.21%。

有色噪声；惯性测量单元；卡尔曼滤波；行人导航；步态检测

0 引言

随着人类生活方式的改变，人们生活和工作基本都在大的建筑物里面，遇到突发情况断电时，基于无线射频信号的无线保真（wireless fidelity, WIFI）、红外线、超宽带等定位方式都无法正常使用。惯性测量单元（inertial measurement unit, IMU）的数据输出不易受环境的影响、具有自主性，根据IMU可推算出行人位置[1-2]。基于IMU的惯性行人导航方法，按照原理可划分为行人航位推算（pedestrian dead reckoning,PDR）和捷联惯性导航系统（strapdown inertial navigation system, SINS）[3]解算。SINS根据IMU输出的加速度进行积分并与零速检测相结合，解算得到位置。PDR主要根据IMU输出数据、步频等特征计算得到步长值，准确估计则需要采集行人的身高、性别、行走习惯等才能确定[4-5]，行走模式比较单一。因此本文采用SINS方法。

由于IMU器件输出存在随机噪声，导航算法存在误差累积[6]等问题，使得IMU的行人导航算法获得的总体定位效果并不理想。陀螺仪、加速度计的输出误差均存在有色噪声[6]。卡尔曼滤波要求量测噪声和系统噪声模型已知，且为白噪声，然而IMU的量测噪声，行人导航系统噪声均不是白噪声，故需要对卡尔曼滤波进行改进。有色噪声建模的方法，通常有成型滤波器法和时间序列分析法；常用的滤波器模型有向量扩充法[7]、一阶马尔科夫模型[8]、随机模型补偿法[9]等。文献[3,5]将这些有色噪声进行简单的线性化后，按照白噪声进行处理，这样会产生较大的误差，有时会导致推算异常[10]。文献[11]采用扩充法，将过程噪声和量测噪声变为白噪声，使用神经模糊网络作为误差估计器，得到卡尔曼滤波的估计误差，对预测结果进行修正。实际上，有色噪声不一定都能表示成白噪声的函数，这些方法很难消除有色噪声的影响，精度有限且容易造成滤波发散。有色噪声在时间上存在相关性[12-13]；文献[14]根据有色噪声相邻历元间噪声相关的特点，在系统噪声和观测噪声均为有色噪声的条件下，对噪声的协方差矩阵进行了改进；文献[15]利用协方差传播定律，改进滤波的估计状态协方差和增益矩阵，来提高滤波精度；文献[16]通过时间序列分析法，对有色噪声进行建模，改进量测噪声为有色噪声情况下的扩展卡尔曼滤波算法。这些方法都是假设相邻历元噪声相关，忽略了不相邻序列的噪声相关性。因此采用基于时间序列分析法的自回归模型（autoregressive model, AR）对噪声进行建模，推导出有色噪声的改进卡尔曼滤波算法；零速区间IMU的计算速度作为改进卡尔曼滤波的量测值，将改进卡尔曼滤波得到的估计值与惯性导航系统（inertial navigation system, INS）解算相结合构建行人导航算法，来提高定位精度。

1 改进的有色噪声卡尔曼滤波模型

1.1 有色噪声及其模型的建立

白噪声是一种理想化的噪声，实际工程中十分少见，历元间互不相关，协方差为零。在工程项目中经常遇到的是有色噪声，有色噪声具有噪声序列中、任意一个时刻与另外一个时刻相关的特性[8,15]。在某些特定情况下，有色噪声可以直接采用白噪声进行简化替代，以减少计算复杂程度。成型滤波器具有通用性，且精度有限，由于采用时间序列分析法，可以直接对噪声进行高精度建模，故本文采用时间序列分析法进行建模。

根据文献[7，13]对基于微机电系统（micro-electro-mechanical systems,MEMS）型IMU的误差分析，IMU的噪声包含随机常数、白噪声和有色噪声，即输出噪声可以描述为

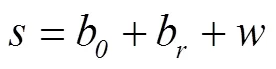
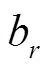
表1 AR(1)、AR(2)、AR(3)及AR(4)的AIC值

1.2 改进的有色噪声卡尔曼滤波算法

将非线性离散系统的状态方程和观测方程表述为

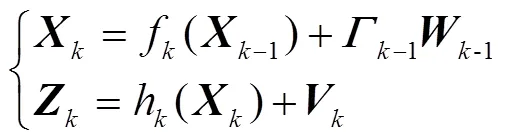
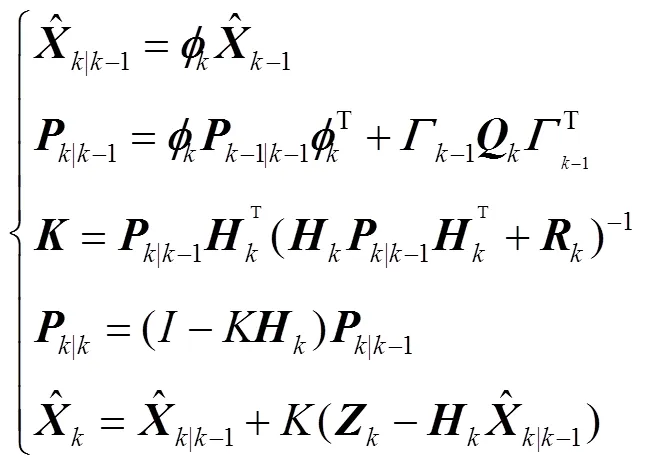
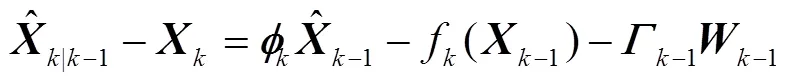
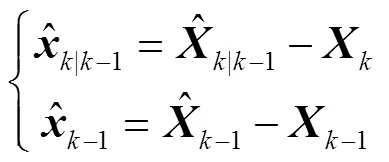
将式（8）代入式（7）可得

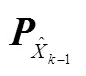
因为

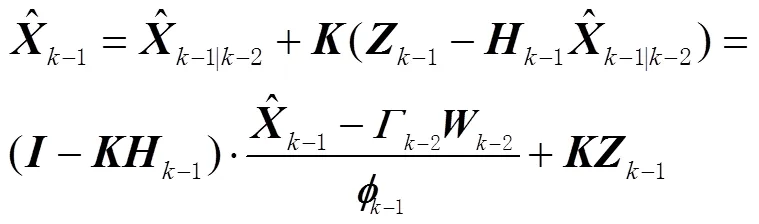
根据协方差传播律[15]可得

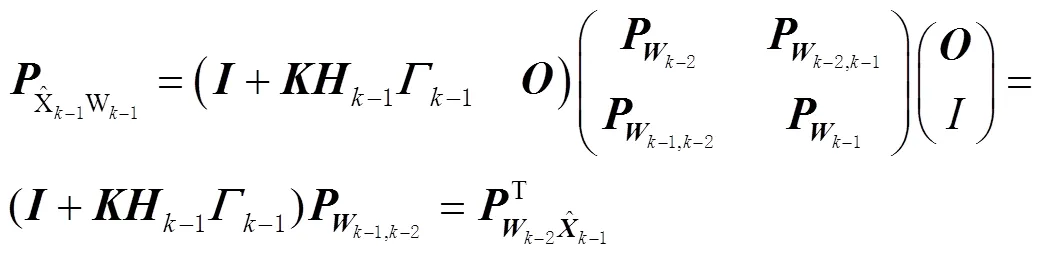
式中为零矩阵。

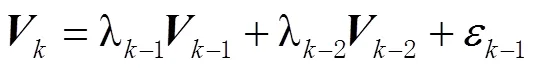
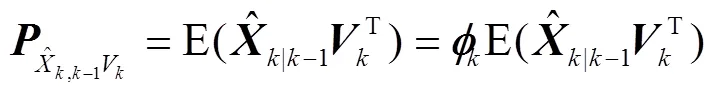
因为

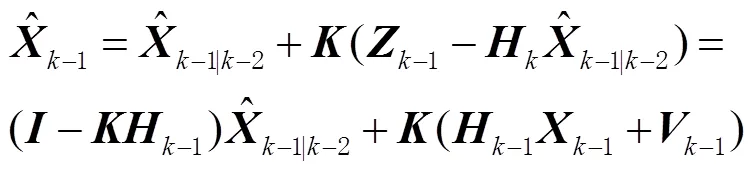
根据协方差传播律[15]可得

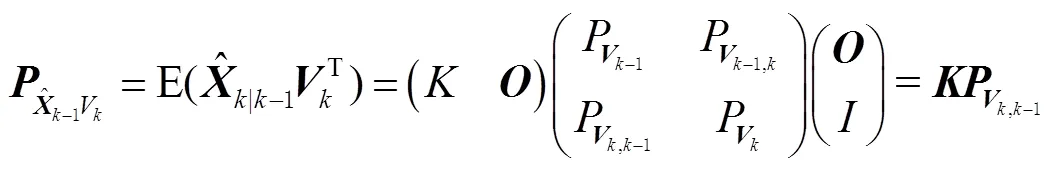
将式（16）代入式（14）可得

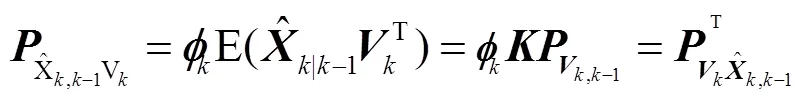
根据文献[15]中的极大后验估计计算式，建立改进的状态估值方程为

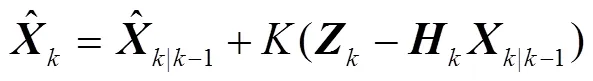
其中：

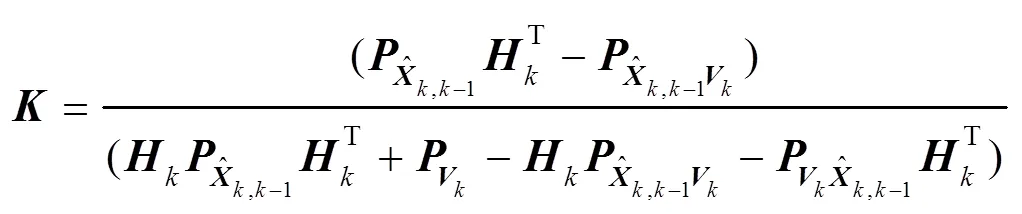
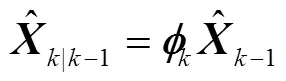
结合传统扩展卡尔曼滤波协方差更新公式，并考虑有色噪声的影响，则改进后的协方差公式为

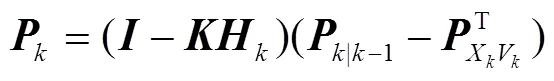
其中

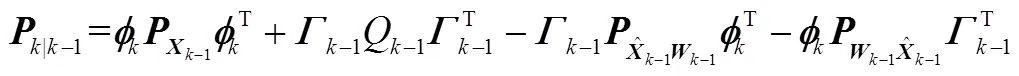
式（12）、式（17）至式（22）为改进后的基于有色噪声的扩展卡尔曼滤波公式。

2 行人导航系统的设计

2.1 系统框架

根据已知初始静止位置信息及使用IMU的磁力计、加速度计、陀螺仪进行静态初始对准，获得初始姿态信息。利用IMU输出的加速度、角速度进行步态检测，即零速区间的判断。若检测结果为零速区间，则对速度进行零速修正，同时将IMU计算得到的速度作为改进型卡尔曼滤波的量测值；用输出的状态误差对惯性导航算法进行修正，以此推算出后一时刻的位置、速度、姿态等信息。行人导航系统如图1所示。

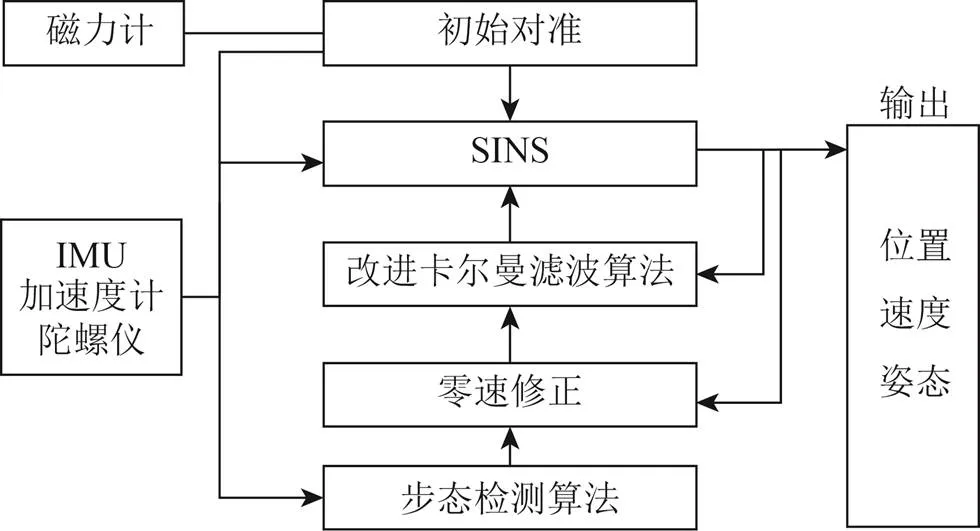
图1 行人导航系统框图

2.2 步态检测

行人连续行走时具有明显的周期性和规律性，两脚交替着往前跨步，本文将左右脚各往前迈一步视为一个复步运动，即两步，行走步态图[18]如图2所示。从图2中可知：中脚跟着地①到中脚跟离地④期间，右脚均未离开地面，这期间被称为支撑期；脚尖离地⑤后，右脚开始往前摆动，直到右脚脚跟着地⑦，这期间称为摆动期；③和⑥分别为右脚支撑左脚往前跨步、左脚支撑右脚往前跨步的某一时刻步态。右脚刚接触地面，逐渐产生摩擦力，到右脚掌着地时，摩擦力最大，右脚速度为零；同时在步骤③至步骤④期间，右脚速度为零，因此将该区间称为零速区。

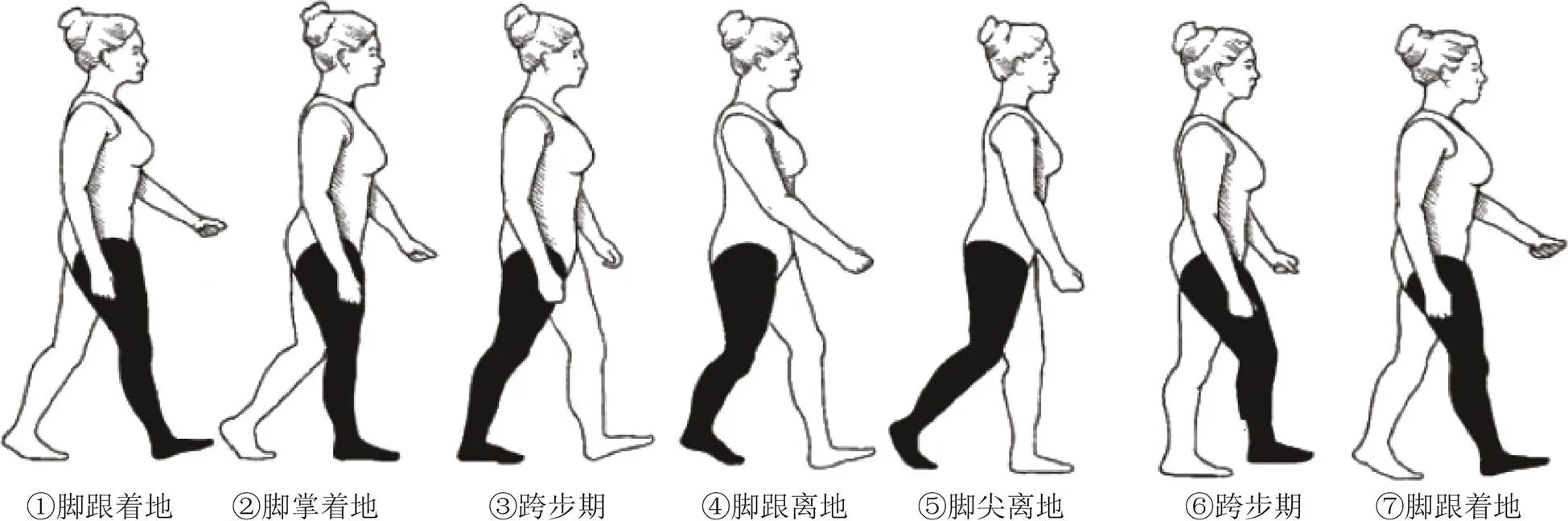
图2 行走步态图[18]

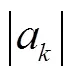
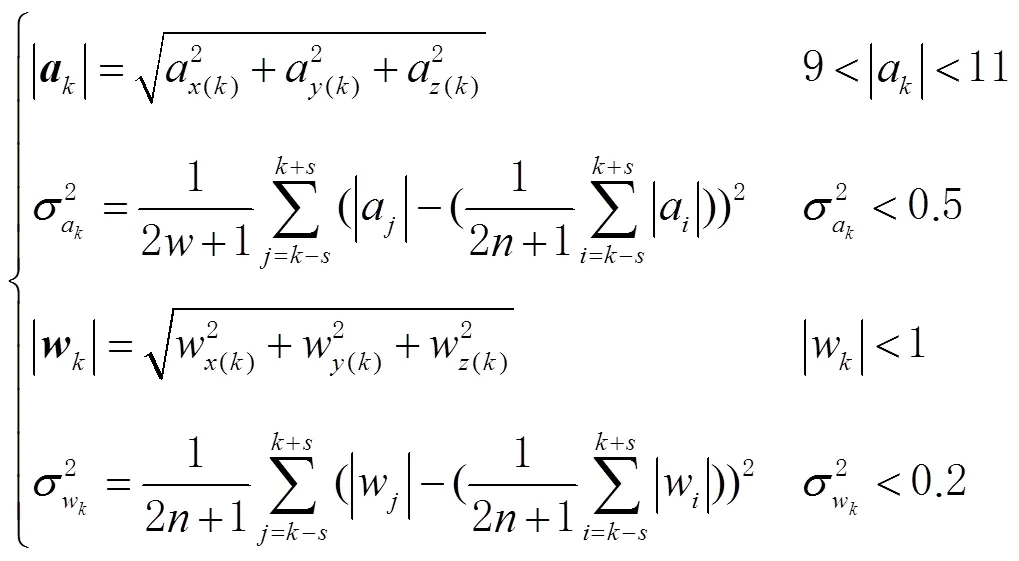
2.3 行人导航算法

在静止状态下，初始的位置已知、速度为零，利用加速度计和磁力计求得IMU的初始姿态角[19]；在静止60 s后，采用加速度计和磁力计的输出值，计算IMU的初始姿态、加速度计和陀螺仪的初始误差。由于方法比较固定，不展开详细叙述，详细论述见文献[17]。

在已知当前时刻的位置、速度、姿态信息的前提下，根据陀螺仪和加速度的输出以及卡尔曼滤波的状态误差估计，可推算出下一时刻的信息，主要有以下4个步骤：

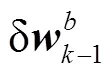
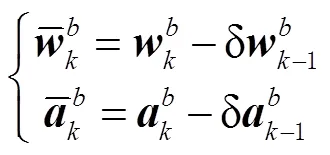
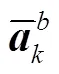
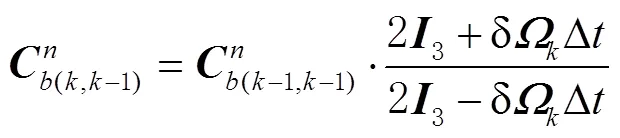
3）消除本地重力的影响，即

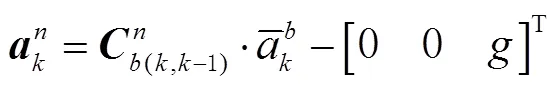
4）估计时刻的位置、速度、姿态。时刻的速度、位置的估计值为

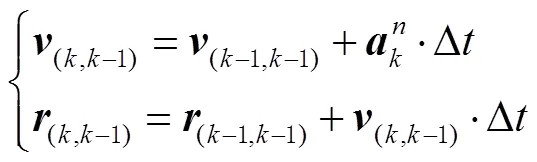
2.4 改进型卡尔曼滤波的应用

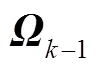
3 实验验证

实验采用克森斯（XSENS）公司的运动跟踪模块（motion tracking module, MTi），其主要器件包含有三轴陀螺仪、加速度计和磁力计，其传感器性能如表2所示。

表2 传感器的性能指标

将MTi绑在实验员的脚背上，实验员围绕事先已经测量好的长方形走廊正常行走并进行数据采集。MTi的采样频率设置为100 Hz，初始对准时间为60 s，实验员通过数据线将实时采集到的数据上传到电脑。为了验证本方法在长距离方面的优势，实验选取的路线比较长，实验场景及器材如图3所示。

图3 实验场景及器材图

实验场地位于信工楼6楼的B区环形走廊，实验路径为38 m×60 m的闭合矩形。实验员沿着靠近建筑内侧的走廊中间进行数据采集，共进行6组。实验轨迹设计的直角转弯处，行人运动状态发生变化，误差也会随着发生改变，这有利于验证算法的性能。

图4为第三次实验结果路径对比图，图4中的实线为真实轨迹，传统算法（图中为多段线）为使用基于白噪声卡尔曼滤波模型的行人导航算法，改进算法（图中为点线）为基于有色噪声模型的改进卡尔曼滤波算法下的行人导航算法。从图4可以看出，在第一个直角转弯之后，两种算法的轨迹都开始偏离真实轨迹，这是由于行人运动状态在转弯处发生了变化引起误差增大的后果；而基于有色噪声的改进卡尔曼滤波行人导航算法，对位置误差具有更加优秀的修正效果；改进卡尔曼滤波行人导航算法的轨迹终点，较普通白噪声卡尔曼滤波行人导航算法更接近于实际终点（0,0），这进一步说明，改进的卡尔曼滤波算法能提高行人轨迹的位置精度。

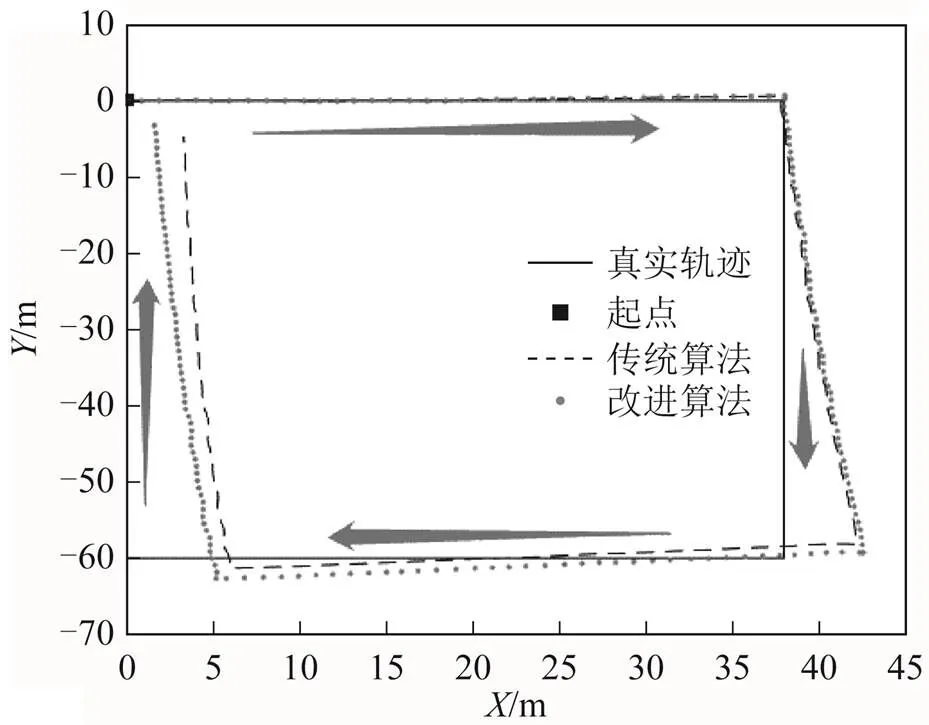
图4 实验轨迹对比图

通过对同一行走路线的多次实验，定位误差结果分布如表3所示。表3中的传统算法，是指基于白噪声卡尔曼滤波模型的行人导航算法，改进算法是指基于有色噪声模型的改进卡尔曼滤波算法的行人导航算法；用解算所得的终点坐标与实际终点坐标（0,0）的距离值表示定位误差；定位误差提高比例是改进算法的定位误差与传统算法的定位误差的差值占传统算法的定位误差的比例。

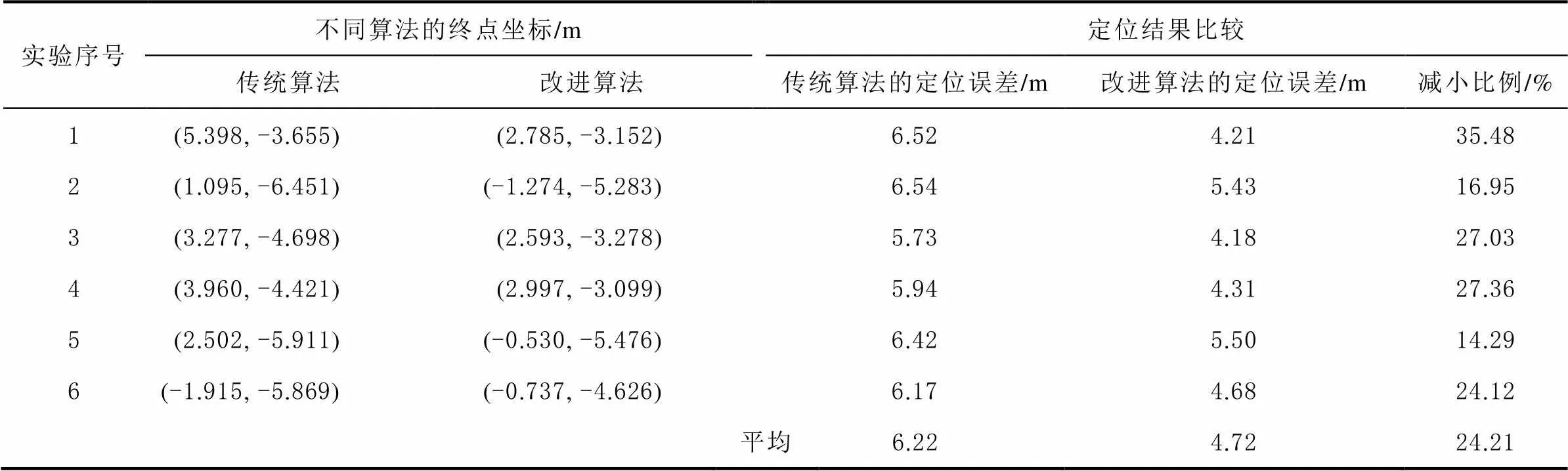
表3 定位误差结果分析表

为便于观察，绘制了如图5所示的定位误差对比柱形图。

图5 位置误差对比图

从图5中6组算法的对比数据可以看出，改进的算法定位误差更小；第2组和第5组数据相对来说误差比较大，经过分析发现，主要原因是这两组行走的步频比正常行走高出了很多。基于有色噪声的改进卡尔曼滤波行人导航算法的平均误差为4.72 m，基于白噪声的传统卡尔曼滤波行人导航算法的平均误差为6.22 m，改进卡尔曼滤波行人导航算法的定位误差减小比例为24.21%，这一结果充分说明了改进卡尔曼滤波的行人导航算法具有更加优异的性能。

4 结束语

根据MEMS型IMU的噪声特点，以及有色噪声不相邻时刻的噪声也存在相关性，采用基于时间序列分析法的二阶AR模型，对有色噪声进行建模，根据该模型对卡尔曼滤波进行改进，基于步态检测、零速修正构建了基于改进卡尔曼滤波的行人导航算法。在长距离矩形路径中进行了6组实验，实验表明，该方法相对于传统白噪声卡尔曼滤波行人导航算法，能提高约24.21 %的定位精度。

[1]DAVIDSON P, PICHE R. A survey of selected indoor positioning methods for smartphones[J]. IEEE Communications Surveys & Tutorials, 2017, 19(2): 1347-1370.

[2]ZHUANG Yuan, HUA Luchi, QI Longning, et al. A survey of positioning systems using visible LED lights[J]. IEEE Communications Surveys & Tutorials, 2018, 20(3): 1963-1988.

[3]赵红宇. 惯性行人导航系统的算法研究[D]. 大连: 大连理工大学, 2015.

[4]田晓春, 陈家斌, 韩勇强, 等. 多条件约束的行人导航零速区间检测算法[J]. 中国惯性技术学报, 2016, 24(1): 1-5.

[5]ZHOU Zebo, MO Shanhui, WU Jin, et al. Behaviors classification base distance measuring system for pedestrians via a foot-mounted inertial sensor[EB/OL]. [2020-04-08]. https: //hal. inria. fr/hal-01929624/document.

[6]宋海宾, 杨平, 徐立波. MEMS传感器随机误差分析及处理[J]. 传感技术学报, 2013, 26(12): 1719-1723.

[7]秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2012, 128-129.

[8]刘俊钊, 林旭, 刘奕凡. 一步相关卡尔曼滤波估计[J]. 测绘, 2018, 41(5): 200-203.

[9]孙强, 惠晓滨, 黄鹤. 一种色噪声下的自适应Kalman跟踪滤波器[J]. 火力与指挥控制, 2011, 36(3): 49-51.

[10]熊雪, 郭敏华, 李伟杰, 等. 基于有色噪声的改进卡尔曼滤波方法[J]. 中国惯性技术学报, 2017, 25(1): 33-36.

[11]宋国东, 姜守达, 林连雷. 复杂有色噪声广义系统信息融合Kalman滤波器[J]. 仪器仪表学报, 2013, 34(5): 1195-1200.

[12]XIA Youshen, WEI Qingquan. An effective Kalman filtering method for enhancing speech in the presence of colored noise[C]//The Institute of Electrical and Electronic Engineers (IEEE). Processing of 2016 International Conference on Audio, Language and Image. Shanghai: IEEE, 2016: 469-474[2020-04-08].

[13]吴永亮, 王田苗, 梁建宏. 基于小波变换的MIMU随机误差建模[J]. 中国惯性技术学报, 2010, 18(6): 660-664.

[14]陈方, 吴小役, 刘文逸, 等. 有色噪声条件下的卡尔曼滤波[J]. 西安邮电大学学报, 2014, 19(2): 56-59.

[15]张奇正, 黄雪梅, 蔡述江. 有色噪声条件下扩展卡尔曼滤波算法研究[J]. 计算机仿真, 2019, 36(6): 273-276.

[16]NASSAR S, SCHWARZ K P, NOURELDIN A, et al. Modeling inertial sensor errors using autoregressive (AR) models[J]. Navigation, 2004, 51(4), 259-268.

[17]CHANG Guobin. On Kalman filter for linear system with colored measurement noise[J]. Journal of Geodesy, 2014, 88(12): 1163-1170.

[18]钱伟行, 周紫君, 谢非, 等. 基于机器学习与步态特征辅助的行人导航方法[J]. 中国惯性技术学报, 2019, 27(4): 433-439, 447.

[19]殷红. 基于foot-mounted的IMU室内行人航迹推算研究[D]. 南昌: 南昌大学, 2013.

Pedestrian navigation algorithm based on improved Kalman filtering

ZHONG Qilin, ZHONG Weisheng, XIONG Jian, GUO Hang

（School of Information Engineering,Nanchang University, Nanchang 330031,China）

Aiming at the problem that the position accuracy of pedestrian navigation is low due to the influence of the colored noise of the Inertial Measurement Unit (IMU) during pedestrian navigation using the traditional white noise Kalman filter algorithm, the paper proposed a pedestrian navigation algorithm based on colored noise improved Kalman filter: the auto-regressive model was used to model the colored noise of the Micro-Electro-Mechanical System (MEMS) IMU; and the Kalman filter algorithm was improved according to the modeling results; finally the pedestrian navigation algorithm based on the improved Kalman filter was constructed. Experimental result showed that the proposed algorithm would havehigher positioning accuracy than the pedestrian navigation algorithm using the white noise model, and the final positioning accuracy could be improved by 24.21%.

colored noise; inertial measurement unit; Kalman filtering; pedestrian navigation; gait detection

P228

A

2095-4999(2021)02-0028-07

钟启林，衷卫声，熊剑，等. 改进卡尔曼滤波的行人导航算法[J]. 导航定位学报,2021,9(2): 28-34.（ZHONG Qilin, ZHONG Weisheng, XIONG Jian, et al. Pedestrian navigation algorithm based on improved Kalman filtering[J]. Journal of Navigation and Positioning, 2021, 9(2): 28-34.）

10.16547/j.cnki.10-1096.20210205.

2020-04-09

国家自然科学基金项目（41764002）。

钟启林（1994—），男，江西赣州人，硕士研究生，研究方向为行人导航及数据融合算法。

衷卫声（1967—），男，江西宜春人，硕士，教授，硕士生导师，研究方向为组合导航、仪器仪表及智能控制。