模态质量参数测试方法研究

杨正玺，常洪振

(1.北京机电工程研究所，北京100074；2.北京强度环境研究所，北京100076)

0 引言

结构动力学方程包括结构的质量矩阵、刚度矩阵和阻尼矩阵。其中,质量矩阵储存着结构各部分的动能,刚度矩阵存储着结构各部分的势能,阻尼矩阵则代表能量在结构的各部分之间的转移(例如机械能转化为内能),结构的总能量通过这三个矩阵进行相互转换,由此形成结构持续的运动(振动),结构共振时的形态,称之为模态。

结构动力学中的模态对应实际物理意义上的振动形态,在数学意义上则对应非齐次微分方程的特征值问题。结构动力学模型对应的方程在物理坐标系下,质量矩阵和刚度矩阵均是非对角的对称正定矩阵,若直接求解方程难度较大。通常的做法是,借助模态向量基的正交性将结构实际的非对角质量矩阵和刚度矩阵转换为对角矩阵,这样就可以将结构在物理坐标系下的多自由度系统解耦为n个单自由度组成的系统,由此方程求解可大为简化。上述解耦过程得到的模态坐标系下的对角质量矩阵和刚度矩阵就称为模态质量阵、模态刚度阵,每个对角元素称为结构该阶模态质量、模态刚度。

模态质量和模态刚度是为了数学计算的方便在模态坐标系下的定义,不再具有实际的物理意义和量纲。不过由于其也是对实际结构的一种描述,在模态坐标系下得到的这些参数也可通过广义反变换的方式转化为实际物理系下的力学参量[1],即具有实际物理意义。例如在航空航天领域可利用模态质量和模态振型参数来计算飞行器飞行过程的结构动力学方程系数以及动载荷,为控制系统的设计和载荷环境条件的设计提供重要依据[2-5]。由此看来,模态质量和模态刚度等动特性参数在航空航天领域的结构动力学设计中占据着重要的地位。基于此,一些学者已经提出基于有限元模型获取模态质量和模态刚度的方法[6-9],但该方法的测试结果极依赖于所建立有限元模型精度,对于一些复杂结构的完整的有限模型难以建立,因此该方法有很大局限性。由于模态质量和模态刚度可以通过结构固有频率相互导出,本文仅研究模态质量获取方法,其中重点研究试验测试方法。

1 公式法

根据定义,模态质量矩阵等于结构物理坐标系下真实的质量矩阵左乘模态振型矩阵的转置,右乘模态振型矩阵为

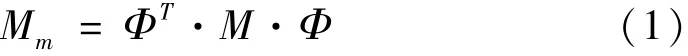
式中:Mm为模态质量矩阵;M为物理坐标系下真实的质量矩阵;Φ为模态振型;ΦT为模态振型矩阵的转置。

式(1)中,需已知结构物理坐标系下真实质量矩阵,对于复杂结构,需先建立有限元模型,物理坐标系下真实质量矩阵、模态振型均可通过有限元模型提取。考虑到有限元模型与结构相比有一定误差,获取的模态振型也会有误差,并且直接通过完整的有限元模型提取的参数容量一般较大,不便于直接计算。工程中通常使用的方法是利用试验实测振型数据和有限元模型提取的物理坐标系下真实质量矩阵配合进行计算,公式中的模态振型矩阵由试验来给出,真实质量矩阵通过有限元模型缩聚到试验测点处的缩聚模型给出,这样就极大减少计算量,同时提高结果的准确性,但该方法仍需要建立结构的有限元计算模型,因此,该方法对于复杂结构存在一定使用局限性。

2 基于频响函数的试验方法

2.1 方法原理

根据模态理论,在比例粘性阻尼假设下,n自由度系统用模态参数表示的加速度频响函数矩阵为

式中:ω为固有频率;{φ}i为第i阶模态的振型为第i阶模态振型的转置;Mi为模态质量;Ki为模态刚度;Ci为阻尼系数。

简单的单点激振情况下,上述矩阵的第l行第p列分量即在p点激振,l点测量的加速度传递函数为

上述频响函数式子包含了各阶模态参数,对于一般的小阻尼系统,若在模态密度不是很高、相邻模态相互影响不大的情况下,式(3)可简化为

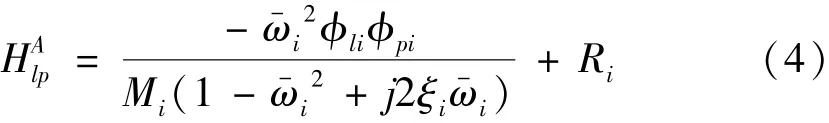
式中:Ri为复常数,表示第i阶以外其他各阶模态影响总和。

将式(4)的实部和虚部分开

当Ri=0时,根据式(5)和式(6)绘制实频、虚频曲线;当Ri≠0,曲线将上移RiR和RiI。这时可直接由图解识别法快速检索求得模态参数,分别确定该阶模态的固有频率ωi和模态阻尼比ξi。

2.2 锤击法

若试验采用锤击法,振型测量可由频响函数矩阵中一行的虚部峰值得到。若将余项Ri当做小量忽略,再令即在共振频率处,则由式可得传递函数虚部峰值点的值为

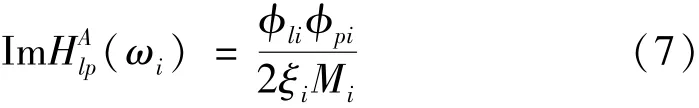
锤击法为响应点l固定,激振点p=1,2,3…n时,令其中m点为归一化参考点,即φmi=1,参考点m的频响函数虚部峰值为

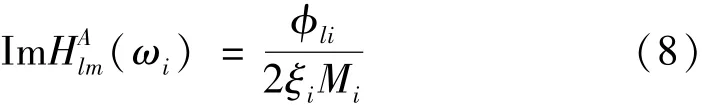
第p点的归一化后振型为

整理可得锤击法中该阶模态质量计算公式为

当响应点与归一化点一致时,模态质量计算公式为

2.2 激振器法

若试验采用激振器法,推导过程与锤击法类似,激振器法中模态质量计算公式为

当激振点与归一化点一致时,计算公式(12)与式(11)一致。

2.3 模态质量的修正

由式(10)～(12)可以看到,模态质量的测试精度直接取决于阻尼比ξ和频响函数H的测量精度。对于阻尼比的精度,影响因素主要包括各阶模态的分离程度、测试中所使用窗函数以及测试设备本身的频率分辨力。在测试中可通过优化激振位置尽量使各阶模态分离,使分析频段内仅为单一模态,以提高阻尼比识别的准确性。对于测试设备的频率分辨力则要求每次测试分析频率上限值根据各阶模态频率分别设定,并且尽可能选择低的上限。

频响函数是有量纲的,虽然试验系统中的力和加速度传感器一般都要求使用提供的灵敏度标定值,但通常计量部门所做的标定是在静载下或特定频率下的。频响函数测试是一个动态过程,频率范围广,传感器灵敏度将会发生变化,特别对于力传感器,锤击法中所测得的力值是锤头和传感器之间的力,并不是直接作用于结构上的力,它与所使用力锤的重量、锤头以及结构的材质都有关[10-11]。为保证频响函数测试的准确度,测试前需要先对所用的测试设备作组合动态标定。

通常采用文献中介绍的标准质量块绝对标定法。如图1所示,标定过程所使用的测试系统与模态测试系统相同,只是将结构试验件改换为标准质量块或砝码。

图1 修正方法示意图

将砝码用橡胶绳悬吊起来,在砝码的一个端面中心粘贴加速度传感器,另一端面中心作为锤击点或激振点,在锤击点或激振点位置粘贴一片与实际结构相同的材料。标定过程的分析仪频率上限取模态测试时可能采用的最高频率,窗函数甚至指标都应与模态测试时相同,会对标定结果产生较大影响。标定过程与模态测试相同也取多次测试平均,次数可适当增加。标定结果曲线为一条有小幅波动的水平直线,可在所标定的频率范围内取若干点的平均值作为最终标定值。根据牛顿第二定律,质量为m的砝码,自身频率足够高,在所标定的频率范围内,其频响函数应与静态时一致,为1/m,故系统的标定系数可写为

模态试验直接测得的频响函数值H试,可由式(13)修正为实际的频响函数值

将式(14)代入式(10)和(12),可得模态质量的修正结果。

3 基于频率变化率的试验方法

上述基于频响函数的试验法存在不足:一是要测定准确的阻尼比值,对于密集模态情况需要多次优化激振位置,工作量大且效果有限,阻尼比的准确度难以保证;二是测定准确的激振力和响应的幅值,要求传感器和测量仪器有准确的灵敏度标定值,传感器和测量仪器通常仅在计量部门所做的静载或特定频率下的标定值是不够的,需要在模态测试前对实际使用的测量系统作组合动态标定,较为繁琐。本节所介绍的基于频率变化率的试验方法不需要测量力幅和振幅的绝对值,避免了标定程序,更为简便可靠。

首先使试件处于某阶模态共振点,然后在试件上一点或若干点上逐级增附加质量,改变激振频率,重新建立共振,测量相应的共振频率移动量即可确定模态质量。假设附加质量后试件振型不变,则模态刚度也不变,即

对ωi求导可得

式中:ΔMi为各点附加质量mp与对应的p点规格化振型平方乘积的总和。

为避免偶然误差影响,提高测试准确度,可绘制一条质量变化-频率变化曲线,取得曲线起始点附近的斜率值,将其代入公式中计算模态质量。

由于该方法假设附加质量后试件振型不变,即模态刚度不变,因此附加质量的大小不应过大,参考飞行器相关模态试验标准[12]中对于边界支承工装所产生的附加质量要求的规定,本文定性给出该方法中附加质量的大小应小于试验件质量的1%,供使用中参考。

4 应用实例

采用梁结构进行试验测试方法验证,尺寸为长1500 mm×宽100 mm×厚3 mm,模态质量以右端部所在位置归一化,主要考虑梁的前三阶模态。首先建立有限元模型以利用公式法计算模态质量,并以此结果作为评定试验方法获取结果的基准。

进行锤击法自由模态试验,在右端部和中间位置布置两个响应测点,变换锤击点进行模态测量,梁结构实物如图2,有限无模型图3所示。

图2 梁结构实物图

图3 梁结构有限元模型

重点获取准确的传递函数曲线并识别模态阻尼比参数,并利用砝码对传感器和测试系统进行联合标定,如图4利用锤击方法计算模态质量。

图4 传感器和测试系统的联合标定

重新进行锤击法自由模态试验,在右端部即归一化点处逐级粘结不同质量的砝码(如图5),然后重新测量结构的共振频率,利用第3节介绍的方法作出质量变化-频率变化曲线,如图6所示,取得曲线起始点附近的斜率值代入第3节公式中,计算模态质量。

图5 梁结构上附加不同质量的砝码

图6 模态质量变化-频率变化曲线

两种试验方法得到的梁前三阶模态质量结果与公式法计算的基准的对比(括号内为误差百分比)见表1所示。

表1 两种测试方法与公式计算基准结果对比

由表可知,频响函数法得到的结果除一阶模态误差为15%外,二阶、三阶结果误差为30%,35%,误差较大;基于频率变化率的试验方法得到的结果各阶模态误差均可控制在20%左右,能够满足实际工程的需要。

5 结论

基于有限元模型的公式法获取模态质量在工程中仅局限于简单结构的使用,本文对基于频响函数、频率变化率获取模态质量参数的试验测试方法进行了研究,并应用于实际梁结构,对两种试验测试方法获得的结果与公式法计算的基准结果进行对比,表明基于频率变化率的试验方法得到的结果误差可控制在20%左右,能够满足实际工程的需要,为获取复杂结构模态质量参数提供了可行的方法。