转动惯量在线测量用涡卷弹簧的设计

仝哲旭，彭军

(航空工业北京长城计量测试技术研究所，北京100095)

0 引言

平面涡卷弹簧又称发条弹簧,使用时一端固定,另一端作用扭矩,在扭矩的作用下,弹簧在平面内发生扭转。平面涡卷弹簧根据相邻圈弹簧之间是否相互接触分为接触型和非接触型两种,接触型涡簧由于卷绕圈数多、变形角大,可在较小的体积内储存很大的能量,常用来做蓄能机构,比如作为力补偿装置、原动装置等;非接触弹簧常用来提供反作用力,可用来作扭摆法测转动惯量的动力源[1-2]。

转动惯量是表征刚体转动特性的一个重要物理量,在航天、航空、汽车、船舶、机械等多个领域经常需要测量物体的转动惯量。因此,转动惯量的准确测量具有十分重要的意义。转动惯量的测量方法有线摆法、落体法、扭摆法等,其中扭摆法测量精度较高,多用于测量大中型构件。

文章所要测量的正弦扭矩标准装置气浮轴系的转动惯量,精度要求高,且结构复杂不易拆下单独测量,因此设计非接触型平面涡卷弹簧(以下简称涡簧),应采用扭摆法在线测量其转动惯量[3]。

1 涡簧测转动惯量原理

采用扭摆法测量气浮轴系的转动惯量,因气浮轴摩擦阻力很小,在不考虑阻尼的情况下,可认为气浮轴作自由振动。分别在空载、加一块砝码、加二块砝码、加三块砝码和加四块砝码五种情况下进行测量,采用光栅测量并解算扭摆运动周期,从而计算得到涡簧弹性系数和空载时转动惯量的值。加载到气浮轴系上的砝码为标准砝码,其转动惯量和质量已用质量特性标准装置测量得到。测量原理如图1所示,扭转涡卷弹簧装在气浮轴的一端,另一端通过紧固机构固定在升降杆上。用外力将气浮轴旋转一定的角度后释放,整个轴系在扭簧的作用下做周期振动[4-5]。气浮轴系的转动惯量公式为

式中:T为振动周期,s;J为标准块惯量,kg·m2;J为轴系转动惯量,kg·m2;K为扭转刚度。

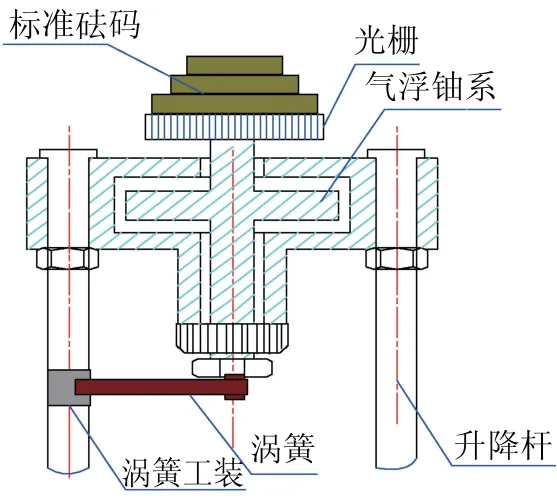
图1 扭摆法测转动惯量示意图

2 涡簧的设计

根据JB/T 7366-94《平面涡簧设计计算规程》进行涡簧设计,首先计算出该涡簧扭矩大小及预设的扭转角,再根据安装要求,确定允许的涡簧宽度及固定方式后来计算其他尺寸参数[6]。

涡簧的扭矩包含被测对象扭摆运动扭矩和阻力矩,扭摆运动扭矩通过气浮轴系空载时的理论值及预设的角加速度来计算,通过气浮轴系的设计结构和使用材料可计算出其质量和转动惯量的理论值,标准砝码的质量和转动惯量在安装之前通过试验测得,标准砝码的参数见表1。

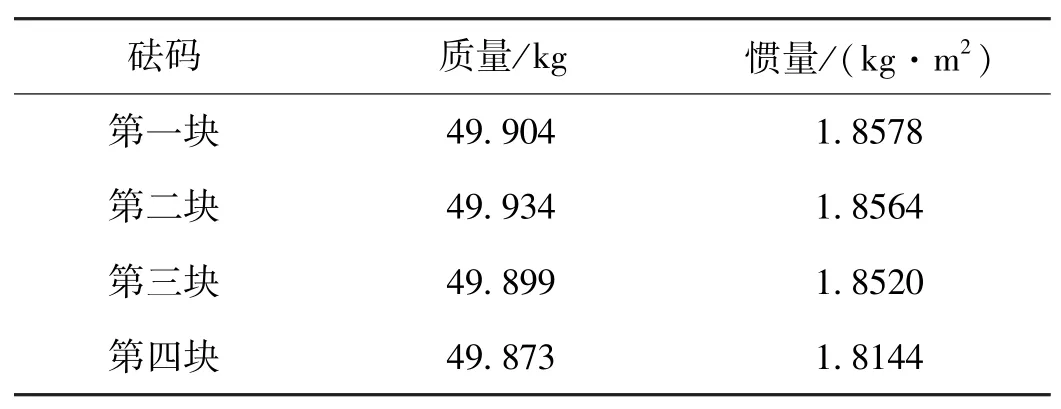
表1 标准砝码参数

取在加载四块标准砝码时的理论转动惯量来计算,预设扭摆运动的频率为0.5 Hz,振幅控制在5°以内,则角加速度为

根据刚体转动定理,气浮轴系在扭摆运动时产生的最大扭矩为J

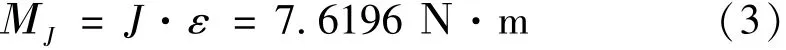
阻力矩包含摩擦力矩和空气阻力矩两个部分,气浮轴系气隙摩擦系数取f=0.0005,取最大加载质量,即加载四块砝码时的摩擦阻力矩大小为

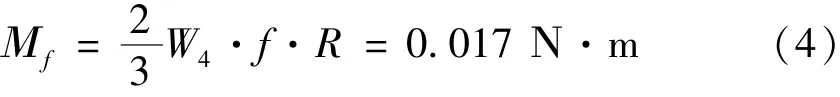
空气阻力矩Mv约为0.2 N·m,则涡簧需要提供的驱动力矩大小为

取涡簧的宽度b为40～60 mm,材料选用65MnI级热处理弹簧钢带,硬度为40～48 HRC,抗拉强度σb为1300 MPa,固定方式为外端固定[7-8],之后根据设计标准计算出涡簧的厚度涡簧工作长度l=内圈半径r=8～15 h。

考虑到涡簧厚度越厚、圈数越多,直径会越大,不便于加工,以及实际安装的限制,初步选择涡簧尺寸参数为宽度50 mm、厚度2 mm、圈数2.5圈、内径277 mm、总长度1956 mm,弹簧设计如图2所示。

图2 涡卷弹簧设计图

确定尺寸参数后,可计算出该涡簧的刚度为

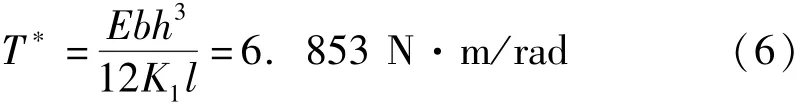
3 涡簧的仿真实验分析

涡簧提供的反作用扭矩的大小和扭转的角度在理论上呈线性关系,特性曲线如图3所示。

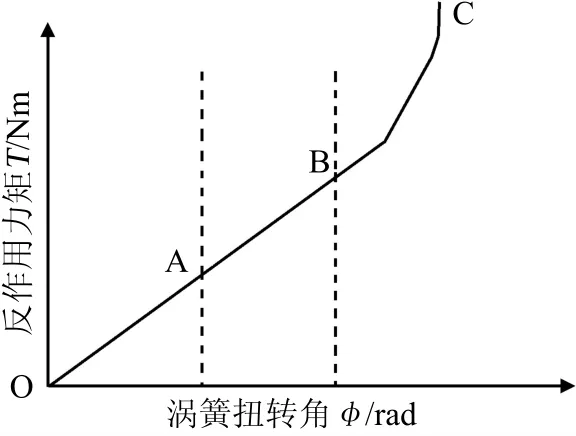
图3 理论特性曲线

图3 中,OA段是涡簧刚承受扭矩时,各圈依次卷紧发生形变;AB段是直至最后一圈发生形变,涡簧开始在全长范围内发生形变;BC段表示扭转角度超过最大许可值后,弹簧各圈全部卷紧,特性曲线变化为渐增型。OA段和AB段都是线性增长阶段,可认为到B点时涡簧在工作范围内已经全部卷紧,BC段为非工作范围。

本文所设计的涡簧圈数少,设计标准中所列出的强度和变形计算式以及相关导出式多为近似式,计算结果与实际情况有一定的误差,尤其是当弹簧圈数小于3时,误差更大,需要通过试验修正[7]。本节通过仿真实验的方法,来计算涡簧的刚度,并验证上文中设计的涡簧能否满足实验要求。

建立涡卷弹簧及其工装模型并把模型导入ANSYS WORKBENCH中,设置材料为弹簧钢,建立的模型及网格划分如图4所示。

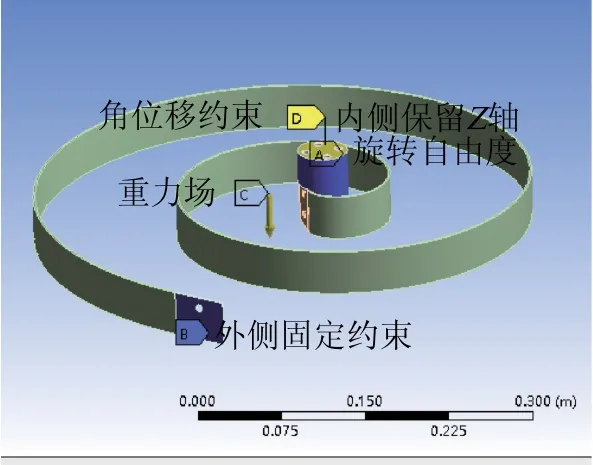
图4 涡簧仿真模型

接下来进行仿真分析,首先在圆柱坐标系下,对涡簧的外端施加固定约束,对内端工装施加递增的角位移约束使涡簧在内端产生同样大小的扭转角,为了接近实际测试情况,还需添加重力载荷;之后在结果处理中,使用探针工具获得涡簧因扭转而产生的反作用扭矩,由扭矩结果和旋转角度计算出涡簧的刚度。多次试验取平均值,数值结果见表2,特性曲线如图5所示。

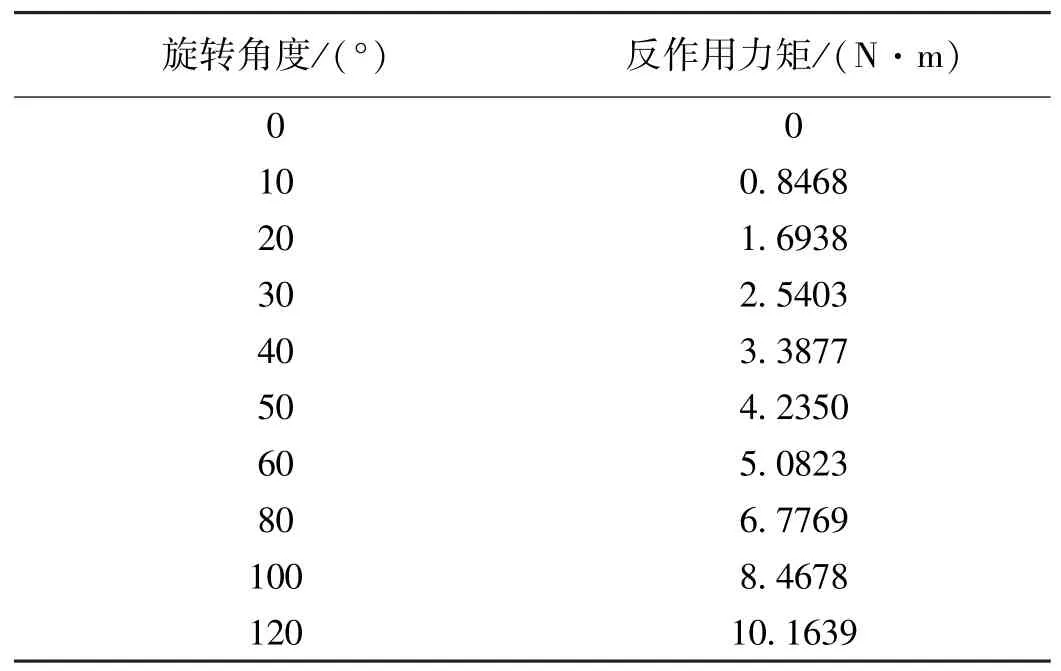
表2 涡簧反作用力矩仿真结果

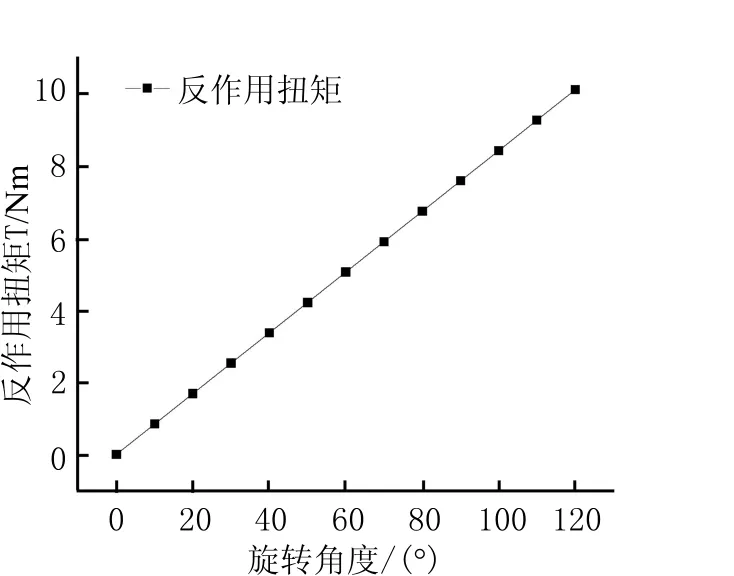
图5 涡簧仿真结果特性曲线

结果表明,本文设计的涡卷弹簧刚度为4.8528 N·m/rad,特性曲线在0°～120°范围内线性度良好;在线性范围内提供的反作用扭矩值能够满足气浮轴系最大加载情况时的反作用扭矩需求[8-10]。同时,仿真计算出的涡簧刚度理论计算结果差别较大,符合设计标准中对3圈以下涡簧计算出的参数误差较大的说明,可通过实际试验进一步测量涡簧刚度。

4 测试结果分析

涡簧的实物及测试安装图如图6所示。进行测试时,首先升起所有砝码,让气浮轴系处于空载状态,之后给气浮轴系一个初始角度,让其在涡簧的带动下作自由振动,测量10次,通过光栅记录振动的周期和幅值并保存;然后依次加载一块、两块、三块、四块砝码,重复上述步骤。涡卷弹簧每次振动的初始幅值均为60°。分别记录气浮轴系在加载不同数量砝码时自由振动的周期,重复四次,补偿砝码加载误差的影响。部分测量结果如表3所示。

图6 涡簧实物图及测试安装图

表3 加载不同砝码时扭摆周期测量结果/s

通过任意两组加载不同砝码时的数据,根据式(7),(8)可解方程得到一组弹簧刚度和气浮轴系空载转动惯量的值。

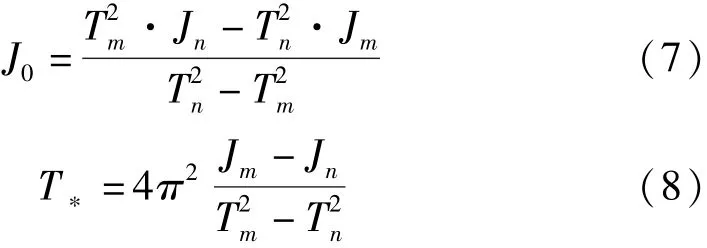
(m=1,2,3,4;n=1,2,3,4;m≠n)

式中:m,n为加载砝码的数量;Tm、Tn分别为加载m块、n块砝码时弹簧自由振动的周期;Jm、Jn分别为加m块、n块砝码的转动惯量之和。

本试验中为了求解两个未知数,每次实验数据可以列出10个方程组,此时方程组有冗余,为了使最可信赖值是在残余误差平方和最小的条件下求得的,可采用最小二乘法求解。最小二乘法是通过从包含误差的直接测试数据,通过数据处理的办法得到间接测量量的最可信赖估计值。最终计算结果为气浮轴系空载转动惯量1.479 kg·m2,测量精度为0.917%,满足1%以内的测量精度要求;涡簧刚度为4.902 N·m/rad,与仿真结果角为一致,符合设计标准中对少圈数涡簧理论值与实测值差异较大额说明。

5 结论

本文基于扭摆法测量原理,按照机械设计标准,设计了一平面涡卷弹簧,用于正弦扭矩标准装置气浮轴系空载时转动惯量的测量。针对设计标准中说明的少圈数涡簧理论参数与实际参数差别较大的问题,通过仿真软件分析了所设计涡簧的刚度,并在实际测试之后对比了理论刚度、仿真刚度和实测刚度,对比结果表明仿真与实测结果一致性良好且都与理论结果差别较大,说明对于少圈数涡簧可在加工之前通过仿真分析方法确定其能满足测量需求。最后,使用该涡簧进行了转动惯量测量实验,测量结果精度较高,说明该涡簧设计合理,测量方案可靠。