基于CFD技术的薄膜热电偶热阻修正模型研究

王玉芳，董素艳，常蕾

(1.航空工业北京长城计量测试技术研究所，北京100095；2.西业工业大学，陕西 西安，710072)

0 引言

表面温度关系到武器装备或试验系统的运行状态,与装备的安全和寿命息息相关,应用于武器装备的设计、生产、使用和维护中。近年来,薄膜热电偶已成为表面温度测量的常用选择之一[1]。薄膜热电偶是通过镀膜技术制备而成的沉积在特定表面上的微米级薄膜,具有热结点薄、质量小、热容量小、对快速变化的温度响应迅速、对原有工况环境温度场干扰小等优点,已广泛应用于表面瞬态测温领域,包括航空发动机内表面温度测试、汽轮机一级叶片表面温度测试、火箭燃气喷嘴壁面温度测试等[2-7]。

目前薄膜热电偶多用于各种异形表面温度的测试,比如弯曲表面、微小区域等,但由于粘贴胶层厚度、环境温度等变化,对薄膜热电偶的测试准确性提出了挑战,需要对这些影响因素导致的温度偏差进行修正。针对薄膜热电偶的现场校准问题,本文以选定的热电偶模型为研究对象,开展不同表面温度下由胶层厚度引入的测量误差的CFD数值仿真和试验研究[8-11],得到表面温度、胶层厚度与热阻修正之间的对应关系,并在此基础上建立热阻修正模型,为现场测量中薄膜热电偶的热阻修正提供技术依据。

1 薄膜热电偶几何模型及网格创建

在采用薄膜热电偶进行表面温度测量时,薄膜热电偶通过胶接工艺粘贴在被测物体表面,为减少对热传导的影响,理论上用于粘贴薄膜热电偶的胶层厚度越薄越好。受现场胶接工艺的影响,目前最薄胶层厚度为1 mm。热阻修正模型如图1所示。

图1 热阻修正模型

薄膜热电偶各膜层采用磁控溅射或电子束蒸镀方法溅射。镀制完成的热电偶结构如图2(a)所示,实物图如图2(b)所示。

图2 薄膜热电偶结构图及实物图

选择膜系材料时应满足:①基底层应厚度较薄、膜层致密并且可弯曲;②敏感层应具有良好的热电特性及导热性,在测温范围内具有良好的线性度;③保护层应具有一定电绝缘性,以避免热电偶在使用过程中受外界信号干扰,且保护层需结构致密。根据上述要求,设计的薄膜热电偶膜层结构及胶层厚度如图3所示。

图3 膜层结构及厚度

CFD数值仿真实验设计为:在环境温度为27℃(约300 K)的条件下,对表面温度分别为-30,0,50,100,150,200,250℃,胶层厚度为1,1.5,2,2.5,3 mm的薄膜热电偶进行数值仿真,共计几何模型五个,计算状态35个。

由于计算模型相对规则,故采用六面体网格划分,该方法划分的网格数量相较四面体或多面体划分的网格数量少3～5倍,能够在保证计算精度相同的情况下使数值计算收敛更快,节省计算资源。对壁面及热电偶附近进行网格加密,最小网格尺寸为最大网格尺寸的1/50。对整个计算区域以热电偶为中心进行网格加密,加密增长率为1.02,整个计算域的网格量约为117万。计算域网格整体及局部图如图4所示。

图4 计算域网格整体图及局部图

2 计算方法

湍流模型采用SST k-omega Model,壁面处理方式选用增强壁面类型,CFD数值仿真中介质为空气,在层流条件下流动,因此,需考虑气体可压缩性影响,同时,热容、导热系数、粘性系数均随温度的变化而变化,因此,空气的物性为:密度取理想气体密度值,比热采用分段多项式拟合,导热系数按动力学理论得到,粘度由sutherland公式计算得到。

导热系数设置如表1所示。

表1 导热系数

边界条件设置为:底板(同测量面接触的位置)设置为温度边界条件;薄膜热电偶的最外表面(同大气接触的位置)设置为对流换热边界条件(给出换热系数和环境温度);壁面边界条件设置为无滑移的绝热壁面。

设置操作压力为静压值,设置进口总压为动压值,以减少在低马赫数条件下理想气体可压缩流动截断误差过大的影响。

计算过程中的理论依据是傅里叶导热定律,采用有限体积法求解三维非定常导热方程式,离散格式采用二阶差分格式;计算过程中,当连续方程、动量方程、湍流方程的残差小于10-6,能量方程残差小于10-10,且监测测量截面平均总压不再变化时,则认为计算收敛。

3 计算结果与分析

假设一个表面的实际温度为300 K,当贴上薄膜热电偶后,由于胶层、接触热阻、绝缘层的作用,最终薄膜热电偶的感温端的实际温度为T,则测温偏差为(T-300)K,因此实际测量过程中,待测表面的实际温度为薄膜热电偶的测量温度与存在的测温偏差之和。薄膜热电偶的测温偏差不是常数,会随着测试工况及环境条件变化而变化。

计算几何模型:基底层、敏感层、保护层尺寸不变,胶层厚度分别为1,1.5,2,2.5,3 mm,如图5所示。

图5 计算几何模型

计算工况:静压101325 Pa;环境温度300 K,环境流速6 m/s。

边界条件:底板温度分别为-30,0,50,100,150,200,250℃。操作压力为101325 Pa。

图6 为环境温度为300 K,底板温度为-30℃时的温度云图。可以看出,在环境温度高于底板温度时,由于导热系数的存在,温度沿底板、聚酰胺基底层、热电偶敏感层、保护层逐层上升,测试温度高于底板温度,测试温差为正值。

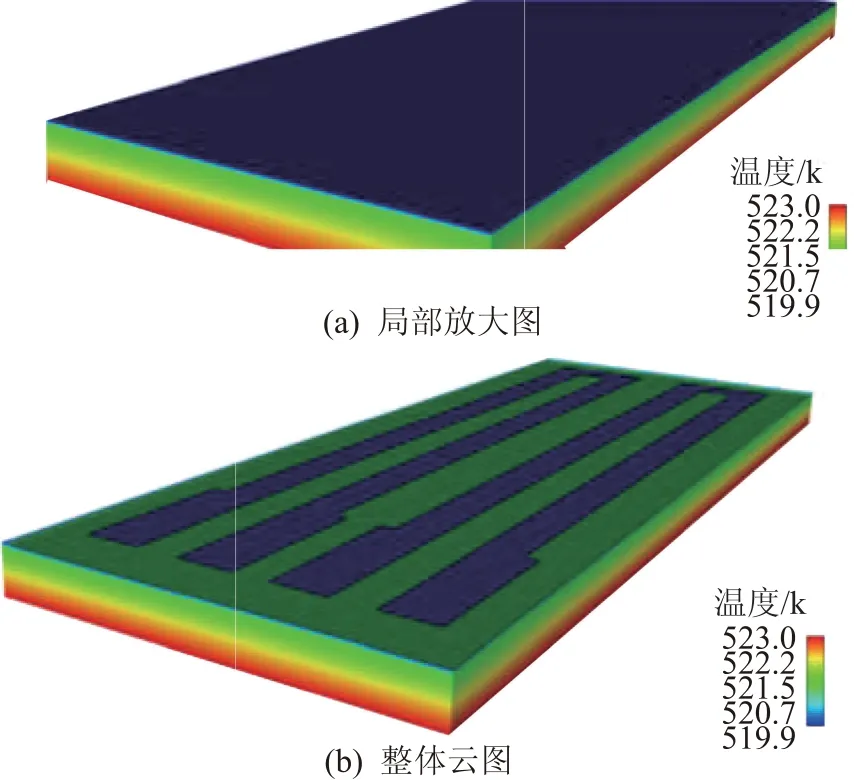
图6 底板温度为-30℃时的温度云图

图7 为环境温度为300 K,底板温度为250℃时的温度云图。可以看出,在环境温度低于底板温度时,由于导热系数的存在,温度沿底板、聚酰胺基底层、热电偶敏感层、保护层逐层下降,测试温度低于底板温度,测试温差为负值。

图7 环境温度为300 K,底板温度为250℃时的温度云图

图8 环境温度为300 K,底板温度为250℃时不同胶层厚度下热电偶敏感层温度云图。可以看出:当计算稳定时,敏感层温度分布基本均匀,随着胶层厚度的增加,测温偏差也随之增加。

定义测温偏差为:ΔT=T表面-T底板,得到相同环境温度下(300 K),不同胶层厚度对应底板温度的测温偏差,如表2所示。

图8 不同胶层厚度下热电偶敏感层温度云图

表2 不同胶层厚度对应底板温度的测温偏差

以热电偶的柔性基底层、敏感层、保护层、固体胶层形成的热阻效应为研究对象,建立热阻修正的CFD数值仿真模型,将表2中的数据绘制为图9。

图9 不同底板温度下测温偏差随胶层厚度变化规律图

由图9可以看出,标准柔性薄膜热电偶的热阻修正值不是常数,它会随着测试工况以及环境条件变化而变化。在相同胶层厚度下,表面温度与环境温度差值越大,薄膜热电偶热阻修正值的绝对值越大,整体变化规律呈线性,且热阻修正值约为温度差值的1%～1.5%;在相同表面温度下,胶层厚度越薄,热阻修正值的绝对值越小,整体变化规律呈线性,且热阻修正值绝对值的最大值出现在胶层厚度3 mm,环境温度250℃处。

4 热阻修正试验研究

开展柔性薄膜热电偶热阻修正试验研究,对薄膜热电偶粘贴到被测表面后的热阻性能进行修正。将薄膜热电偶测温敏感点及引线节点粘贴到表面温度校准器的表面中心位置,如图10所示。

图10 热阻修正试验

环境温度保持为24.6℃,分别在被测表面温度为-30,0,50,100,150,200,250℃的条件下测试标准柔性薄膜热电偶与表面温度校准器的温度值,建立测试温度与热阻修正值之间的对应关系。定义热阻修正值为ΔT=T偶-T底板,试验结果如表3所示。

表3 不同表面温度下热阻修正试验结果 ℃

试验结果表明:热阻修正受被测表面温度的影响较大,随着表面温度与环境温度差值增大,热阻修正值不断增大,这与CFD数值仿真得到的结论一致,但由于CFD数值仿真计算过于理想化,而实际试验中的影响因素较多(例如胶层厚薄不均、粘贴不牢等均会引入误差),试验中得到的修正值偏大,为改善这一状况,未来拟改善试验手段,提高胶接工艺,以得到更为理想的热阻修正模型。

5 结论

对标准薄膜热电偶的热阻修正进行CFD数值仿真研究,以热电偶的保护层、敏感层、柔性基底层、固体胶层形成的热阻效应为研究对象,建立热阻修正的CFD数值仿真模型,结果表明:在相同胶层厚度下,测温偏差大小随着表面温度与环境温度差值增大而增大,与试验结果一致;在相同表面温度下,胶层厚度越薄,测温偏差越小,与实际情况相符。本文的研究将对薄膜热电偶表面测温领域的发展起到推动作用,具有技术借鉴意义。未来将进一步研究表面粗糙度对薄膜热电偶测温性能的影响,以完善热阻修正模型。