基于划分融合的非平衡SVM分类算法
2021-04-21程凤伟
程凤伟
(太原学院 计算机科学与工程系,山西 太原,030032)
0 引言
随着计算机网络技术与通信技术的不断发展,人们能够更快捷、容易、廉价地获取大量的信息,并进行储存,通过分析与处理数据可有效解决分类、回归等预测问题,但如何从大规模数据集中获取有效的信息,成为一个难题。例如在医学诊断[1]、极端天气监测、基因检测、网络入侵检测[2]等领域中存在非平衡数据[3],在这类数据中,样本较少的类称为少数类,样本量大的类为多数类[4],而对于非平衡数据,人们关注的往往是所有记录中的少数数据,一旦将其错误分类,将会带来不可估量的代价。传统的分类方法在处理这类数据时,往往会忽略数据的非平衡性,将非平衡数据集中的少数类预测为多数类的类别,而忽略了重要的少数类,因此,如何对非平衡数据进行正确分类,提高少数类的分类精度,仍然面临很大的挑战。
由于传统机器学习算法在处理上述问题时效率低下,增量学习算法可以从数据集中挑选一部分样本来进行学习,通过学习,找出数据之间的联系,通过它们之间的联系,构建初始数据模型,通过初始模型对后续数据进行学习,通过学习,更新原有模型,通过反复学习,完善模型,使模型最优化。这种采用样本分批次的方式可以将大规模的复杂机器的学习问题转化为小规模的简单求解问题,增量学习对于动态数据和数据更新的处理有着良好的表现[5],目前,增量学习已被广泛用到非平衡数据的处理上。
对于不平衡数据集,我们一般将少数类样本当成正类样本,多数类样本当作负类样本。针对这类数据集的分类问题,已有国内外学者提出了两类优化模型:一类是基于训练样本采样的优化模型,其中又分为正类样本的上采样[6-7]、负类样本的下采样[8-9]以及二者相结合的混合采样[10-11]方法;另一类是权值调整模型,典型的方法有损失函数加权法[12]和样本权值调整法[13]。基于训练样本采样的优化模型,在处理非平衡数据集时,由于对数据进行盲目、随机采样,容易造成分类器的过拟合或样本信息的丢失;而传统的权值调整模型,人为调整权值参数容易造成分类结果的不可解释性,且实验结果随机性强,不易控制。
为了克服采样算法的随机性,本文将增量学习、粒计算、SVM进行结合,提出了基于划分融合的非平衡SVM分类算法,该算法旨在利用划分融合的思想[14]和分类超平面找出重要的、同时剔除冗余的负类样本,以达到平衡数据集的目的。算法首先用k-means对负类样本进行划分,得到一些粒,取粒中心与正类样本一起加入训练集,进行SVM训练,得到初始分类器,再根据负类中粒与分类器的关系,对负类样本进行划分融合,获取更有价值的增量样本,即每次选择最优的负类样本与全部正类样本加入训练集,以修正模型分类器,直到获得满意的泛化能力。
1 DFISVM算法模型
传统分类方法在处理非平衡数据集的分类时,得到的分类器往往会偏向正类样本,即错误地将正类样本预测为负类样本,无法对两类样本进行有效分类,忽略了正类样本的信息,使得到的分类器泛化能力较差。
DFISVM算法针对不平衡数据集中的负类样本进行优化取样,采用增量学习的策略,由于离分类超平面较近的样本有较大可能成为支持向量,而距离分类超平面较远的样本信息对分类几乎没有影响,因此,DFISVM算法通过划分融合的方式,对距离分类超平面近的粒进行深度划分,对距离超平面远的冗余粒进行融合,取划分融合后的样本信息作为增量集,加入训练集进行SVM训练,不断更新分类超平面,以获得最优分类超平面,本文提出的算法能够将参与训练的负类样本始终保持一个较小的规模,有效提高了SVM的训练效率。

由于粒的大小及粒中样本分布差异,密度大的粒中样本分布较为稠密、集中,包含更多的分类信息;密度较小的粒中样本分布稀疏,包含的分类信息相对较少。对于在超平面附近且密度较大的粒,进行再次划分;对于离超平面较远且密度较大的粒进行融合。为了衡量粒中样本的稠密程度,第i个粒的粒密度ρi定义如式(2):
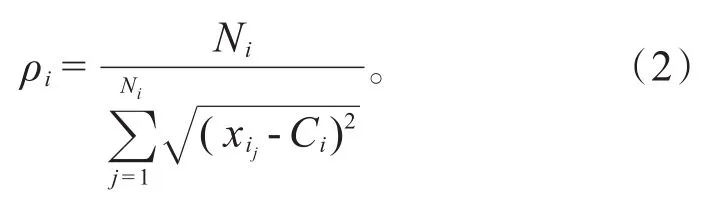
粒半径反映一个粒的大小,第i个粒的粒半径Ri定义如式(3):

经过初始粒划分,将负类样本集划分为E1、E2、E3、…、Ek个粒,提取每个粒的粒中心与全部正类样本一起加入训练集进行训练获得初始分类超平面
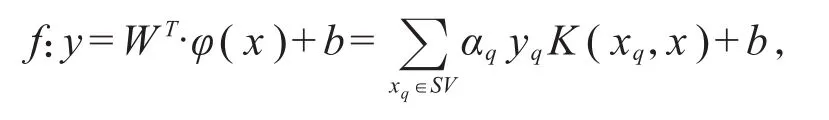
(其中SV是决定超平面的支持向量集,b为超平面的偏移量)。
在SVM训练过程中,增量集的选择主要通过粒到超平面的距离和粒密度两个指标选定粒进行划分融合,离超平面较近的粒更有可能成为支持向量。第i个粒到超平面的距离Di定义如式(4):
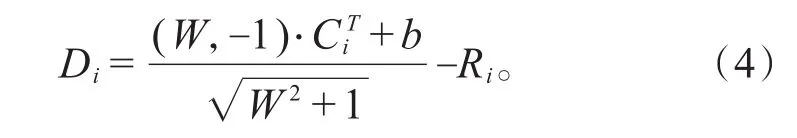
为了方便确定需要划分或融合的粒,给出粒划因子的概念Ki,它有由密度、半径、粒到超平面的距离和调和参数para共同决定,第i个粒的粒划因子Ki定义如式(5):

其中para决定粒需要划分融合的程度,由网格搜索得到,当Ki≥2时,代表第i个粒需要划分,当Ki<1时,代表第i个粒需要与其他粒进行融合。
综上所述,本文提出的DFISVM算法的主要步骤总结如下:
步骤1:用聚类方法将原始数据集中的负类样本集X-划分为k个粒:E1、E2、E3、…、Ek,根据公式(2)计算每个粒的粒中心。
步骤2:取粒中心与正类样本集X+一起放到训练集中进行SVM训练,得到初始分类超平面f。
步骤3:根据公式(2)(3)(4)计算出每个粒的密度、半径和粒到超平面的距离,通过公式(5)计算每个粒的粒划参数,根据粒划参数的值挑选出需要划分的粒进行深度划分,同时,挑选出需要融合的粒进行融合。
步骤4:计算划分融合后的信息粒的粒中心,作为增量集,与正类样本加入训练数据进行再次训练,得到分类超平面:f(x)=WT·φ(x)+b。
步骤5:重复Step3和Step4,直到满足停止条件。
步骤6:算法结束。
DFISVM算法相对于传统SVM分类器而言,考虑到两类样本集规模的差异,提取多类样本中的少量代表点进行训练,提高了SVM的分类效率,同时采用划分融合的方法对代表点进行筛选,使代表点包含更多的分类信息,进而获得更好的泛化能力。
2 实验结果及相关分析
为了验证本文提出的DFISVM算法的性能,将算法与SVM算法及同类的算法ISVM_IL[15]、GSVM[16]、CSVM算法进行比较,本文在7个典型的UCI数据集(见表1)上进行了测试。实验中采用高斯核函数,其中正则参数C取1000,核参数d取1.0。调和参数para由网格搜索算法计算取值为0.2,实验平台为Matalab2016a。
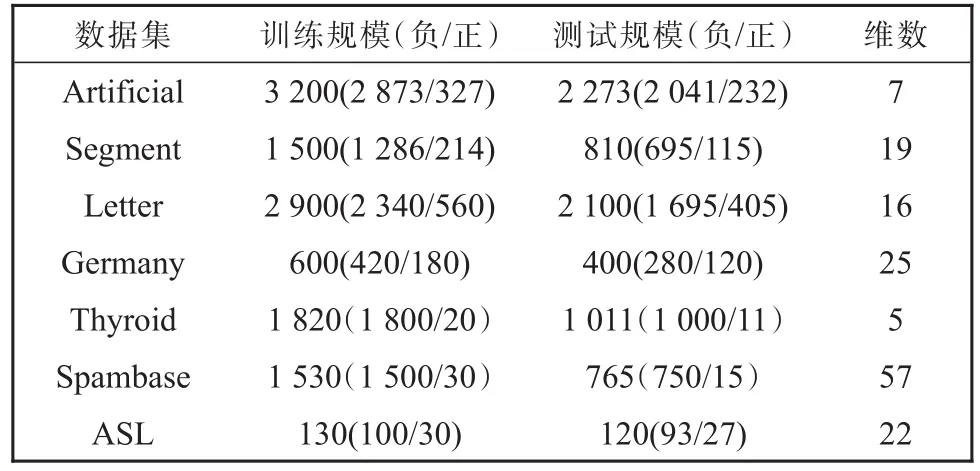
表1 实验采用的数据集Table 1 Datasets used in the experiment
考虑到非平衡数据集的特殊性和复杂性,本文采用非平衡数据问题的一般评价标准分类正确率accuracy、g_means、impor_rate和 sacri_rate[16]共 4 个指标来评价算法的性能。在Artificial、Segment、Letter、Germany数据集上,将本文的算法与SVM算法进行比较,初始粒划参数k取20。实验结果如表2所示。

表2 分类正确率,g_means,impor_rate和sacri_rateTable 2 Accuracy,g_means,impor_rate和sacri_rate
在表2中,本文的算法与传统的SVM算法比较,正确率在多个数据集上只有小幅度提高,且在Germany数据集上有所降低,这说明在提高少数类分类正确率的同时,多数类的正确率可能会有所下降。但相比于准确率,g_means、impor_rate和sacri_rate更能作为非平衡数据的分类评价指标,往往能够显示出一个方法在非平衡数据集的分类性能的好坏,从表2中给出的g_means,impor_rate和sacri_rate实验结果可以看出,DFISVM算法明显优于SVM算法。
为了对比算法的优势,在Thyroid,Spambase和ASl数据集上,将本文的算法与同类的算法进行比较,图1给出了CSVM,GSVM,ISVM_IL和DFISVM 4种算法分类正确率的比较。
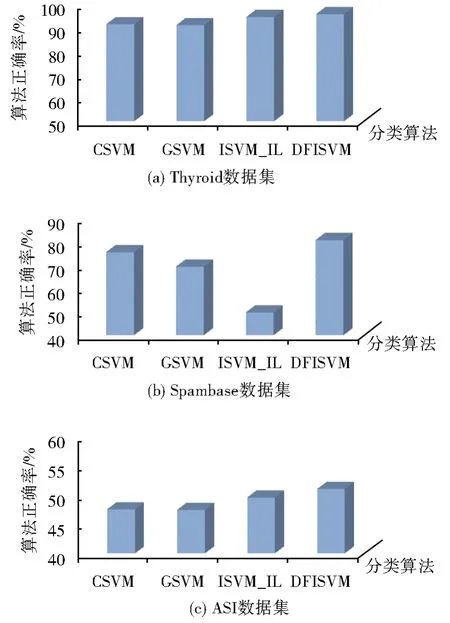
图1 DFISVM算法与CSVM、GSVM、ISVM_IL算法比较Fig.1 Comparison of results among DFISVM and CSVM,GSVM,and ISVM_IL
从图1可以看出,DFISVM算法的正确率在Thyroid和Spambase数据集上都比较高,说明本文采用划分融合的方式选取了更有价值的信息参与训练,取得了更好的分类效果,在ASL数据集上,由于数据集自身局限性,导致DFISVM的算法正确率有所降低,但仍然高于另外3种算法。
图2是CSVM、GSVM、ISVM_IL和DFISVM 4种算法在3个数据集上的实验结果趋势曲线,其中,横坐标为初始粒划参数k的取值,纵坐标为g_means的实验取值,不同颜色曲线代表不同的算法策略。

图2 g_means的变化曲线图Fig.2 Variation curve of g_means
从图2(a)可以看出,在k=10和k=30时,DFISVM算法的g_means的值分别略低于GSVM算法和ISVM_IL算法,在k取其他值的情况下,DFISVM算法的g_means的值都不低于其他3种算法;在Spambase数据集上,除了在k=15时,g_means的值低于CSVM算法,在k取其他值的情况下,DFISVM算法的g_means值都高于其他3种算法;在ASL数据集上,在实验给出的任何k值下,DFISVM算法的g_means值都高于另外3种算法;由此可以说明本文提出的DFISVM算法使少数类的分类性能有所提升;从总体曲线走势来看,DFISVM算法的曲线相对比较平稳,g_means的值受初始粒划参数k的影响较小,说明本文采用划分融合的方法可以有效提取分类信息,克服了算法在采样时的随机性,提高了算法的稳定性。
表3给出了在Thyroid数据集上,DFISVM、GSVM和CSVM 3种算法实验结果的比较,从表3可以看出,与CSVM算法相比,DFISVM算法的g_means和impor_rate两个指标的值都高于CSVM;DFISVM与GSVM算法相比,在k=10和k=20时,g_means和impor_rate两个指标的的值分别低于GSVM,但在k取其他值的情况下,两个指标的值都高于GSVM,从整体看,而且在k取不同的值时,DFISVM大多数情况下3个指标都比GSVM、CSVM要好,而且相对比较稳定。
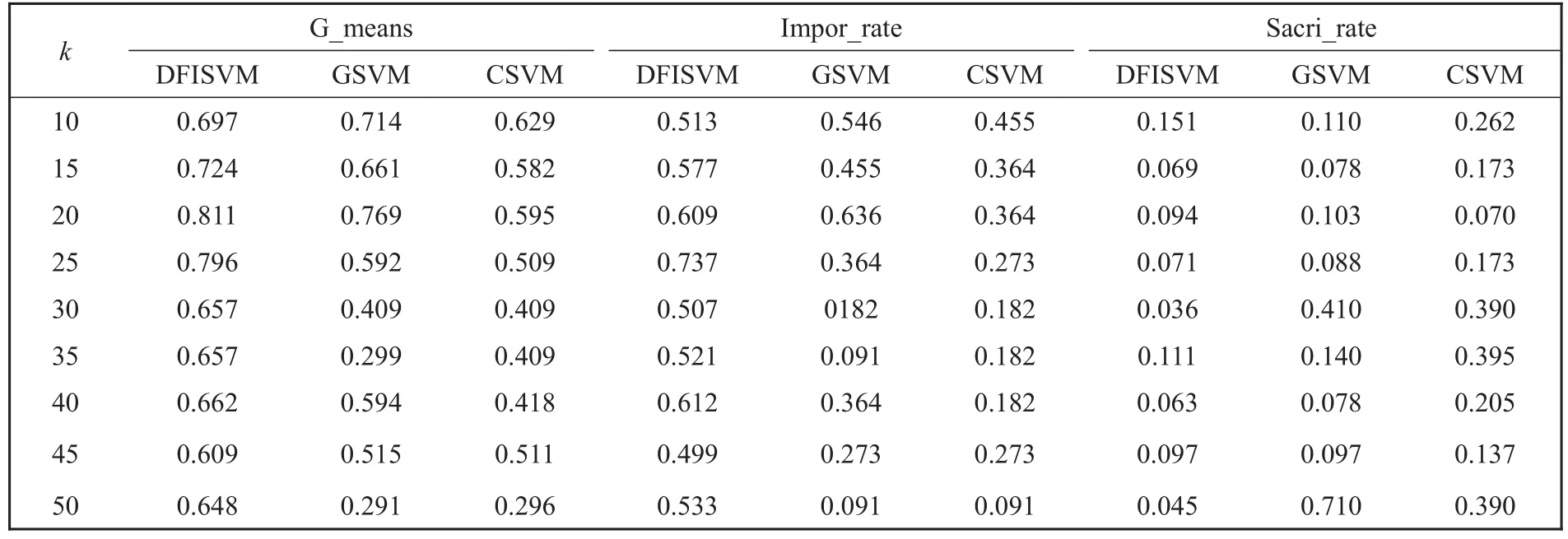
表3 Thyroid数据集上实验结果的比较Table 3 Comparison of experimental results on the Thyroid dataset
表4和表5分别给出了DFISVM和GSVM、CSVM在Spambase和ASL数据集上实验结果的比较。从表4和表5可以看出,DFISVM整体上都要优于GSVM和CSVM算法。
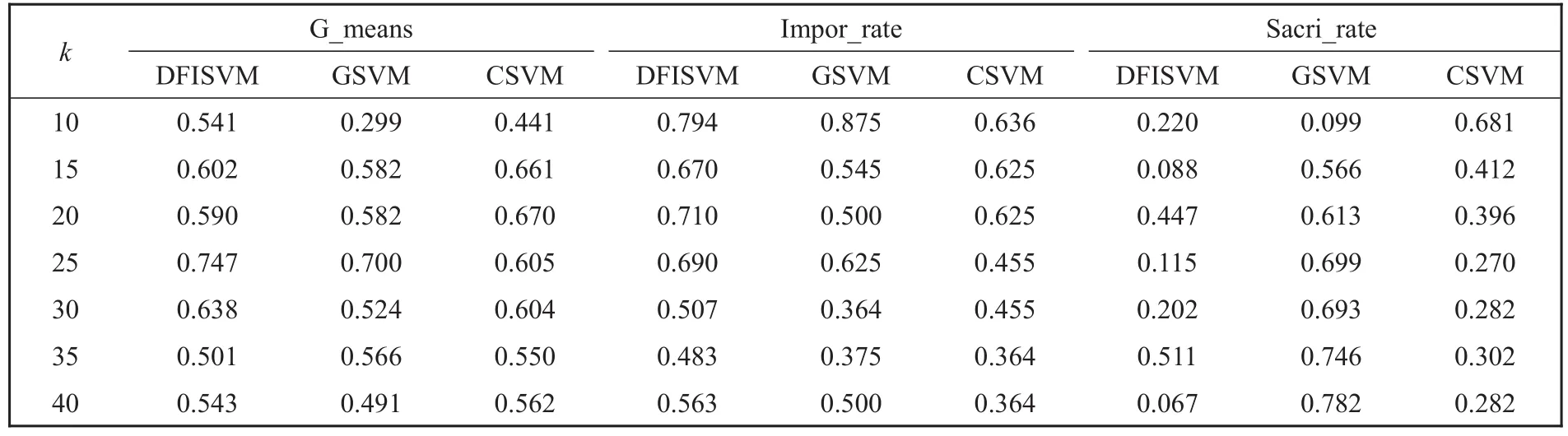
表4 Spambase数据集上实验结果的比较Table 4 Comparison of experimental results on the Spambase dataset

表5 ASL数据集上实验结果的比较Table 5 Comparison of experimental results on theASL dataset
上述实验结果表明,本文提出的基于划分融合的非平衡SVM分类算法,可以有效提取负类样本中有价值的增量样本,DFISVM算法通过划分信息粒,有效提取支持向量样本,通过融和冗余粒,删除大量对分类不起作用的样本,增强了样本分布的平衡性,提高了SVM对于非平衡数据集的分类性能。
3 结论
本文在增量学习的基础上结合划分融合的思想,扩展了SVM在非平衡数据集上应用的能力,通过信息粒再划分,提取更多有价值的信息,同时,冗余粒进行融合,保证了参与训练的负类样本的规模,使样本分布尽量保持平衡,逐步提取负类样本中重要的增量样本,迭代加入训练样本集,提高了非平衡数据集的分类性能,在未来的工作中,考虑将本文划分融合的思想和其他分类算法进行结合,应用到非平衡数据处理中。
