特征标的π-诱导

常学武，李晓娜

（山西大学 数学科学学院，山西 太原 030006）

0 引言

本文只考虑有限群，特征标定义在复数域上。为叙述本文的研究问题和背景，我们需要先概述Gajendragadkar[1]引入的两类重要特征标。

设G为π-可分群，π为素数集合，χ∈Irr(G)为G的一个不可约复特征标。如果χ(1)为π-数，并且对G的每个次正规子群S以及χS的不可约分量θ∈Irr(S)，均有θ的行列式阶o(θ)为π-数，则称χ为π-特殊的特征标，简称为Xπ-特征标，全体记为Xπ(G)。因为G同时也是π'-可分群，故可类似定义π'-特殊的 特征标 ，亦称 为 Xπ′-特征标，全 体记为Xπ′(G)。

下述乘积定理也许是π-特殊的特征标最为基本而重要的性质，亦可见Isaacs最新教材[2]中定理2.2。

Gajendragadkar乘积定理设G为π-可分群，如果α，α'∈ Xπ(G)，而β，β'∈ Xπ′(G)，则αβ∈Irr(G)，进而，如果还有αβ=α'β'，则α=α'，β=β'。

一般地，如果χ∈Irr(G)存在分解χ=αβ，其中α∈Xπ(G)而β∈Xπ′(G)，则称χ为G的一个π-可分解的特征标，简称为Fπ-特征标。G的所有Fπ-特征标的集合记为Fπ(G)。根据上述乘积定理，如果χ∈Fπ(G)，则其因子α和β均由χ唯一决定，分别称之为χ的π-特殊因子和π'-特殊因子。在本文中我们依次记为χπ和χπ'。

目前人们已经发现和证明了很多关于Xπ-特征标和Fπ-特征标的重要性质和定理，并且获得了广泛应用，特别是Isaacs据此创建了π-特征标的理论。仍设G为π-可分群，其中π为某些素数的集合，记为G0的G所有π-元素的集合，称G0上的复值类函数φ为G的一个π-部分特征标，如果存在G的特征标χ∈char(G)使得φ=χ0为χ在G0上的限制。如果一个π-部分特征标不能写成两个π-部分特征标的和，则称为不可约π-部分特征标，简称为Iπ-特征标，全体记为Iπ(G)。根据著名的FongSwan定理，当π=p'时，则Iπ(G)恰为 IBrp(G)，即不可约的π-部分特征标等同于关于素数p的Brauer特征标。此类研究可以参考相关文献[3-8]。

进而，对每个χ∈Irr(G)，Lewis[9]和 Isaacs[10-11]分别构造了共轭唯一的特征标对(W，γ)，满足γ∈Xπ(W)且γG=χ，称之为χ的原核。特别地，当γ∈Xπ(W)时，则称χ为G的一个Bπ-特征标，全体记为Bπ(G)。这是一类非常重要的不可约特征标，不仅可从Xπ-特征标诱导，而且给出了Iπ-特征标的一个典范提升，即特征标的π-限制χ↦χ0给出了一个双射：Bπ(G)→Iπ(G)，据此可将π-部分特征标的研究提升到复特征标情形。值得指出的是，当2∉π时，Dade也定义了一类所谓的Dπ-特征标，并证明了这些特征标也给出了Iπ-特征标的一个典范提升[12]，相关概念见本文第1节。

注意到Bπ-特征标的构造虽然很困难，但总可以从 Xπ-特征标诱导。1997年 Navarro[13]首先研究了这一类特征标，既χ∈Irr(G)满足性质χ=γG，其中γ∈Xπ(W)且W≤G，在奇数阶群中发现了关于Xπ-特征标不可约诱导的新现象，证明了下述三个定理。

Navarro定理A设G为奇数阶群，H是G的子群，并且α∈Xπ(H)使得αG不可约。如果β∈Xπ'(H)，则(αβ)G也是不可约的。

Navarro在该定理的证明中使用了Iπ-特征标的性质，关键是建立了下述重要结果。

Navarro定理B设G为奇数阶群，H≤G，α∈Xπ(H)使得αG不可约。如果J≤G且 |H：H∩J|为一个π'-数，则(αH∩J)G∈Irr(G)。

为了深入探讨Navarro定理A中给出的映射是否为单射Xπ′(H)→Irr(G)，β↦(αβ)G，Navarro考虑了Bπ-特征标，并在此情形下给出了肯定的解答。

Navarro 定理C设G为π-可分群，χ∈Bπ(G)。如果(H，α)是χ的一个原核且β∈Xπ′(H)，则(αβ)G不可约。进而，如果γ∈Xπ′(H)使得(αβ)G=(αγ)G，则β=γ。

本文的主要目标是分别推广Navarro上述三个定理，减弱其奇数阶群的条件，在π-可分群中获得相应的结论。因为Navarro举例说明上述定理均在π-可分群中未必成立，我们将使用特征标的π-诱导（相关定义和性质见本文第1节）代替通常的诱导，同样得到新的不可约诱导现象。本文主要结果如下：

定理A设G为π-可分群且2∉π，H是G的子群且α∈Xπ(H)。如果απG是不可约的，任取βXπ′(H)，则(αβ)πG也是不可约的。

类似地，下述定理是证明定理A的关键，但其本身也是重要的。

定理B设G为π-可分群，2∉π，H≤G，并且α∈Xπ(H)使得απG是不可约的。如果J≤G且|H：H∩J|为一个π'-数，则(αH∩J)πG∈Irr(G)。

最后，为了研究我们定理A中的映射是否为单射，本文在第1节引入了Dπ-特征标的Dπ-原核概念，据此获得了和Navarro定理C相类似的结果。

定理C设G为可分群且2∉π，(W，γ)是χ∈Dπ(G)的一个原核。如果δ1，δ2∈ Xπ′(W)使得

本文使用的群论和特征标理论的术语和符号，可分别参考文献[14-15]。

1 Dπ-特征标及其原核

设G为π-可分群，如果2∉π，则对任意子群H≤G，Isaacs均定义了的一个符号特征标δ(G，H)，即取值为±1的特征标，称为H在G中的π-标准符号特征标。鉴于其定义的复杂性，读者可参考相关文献[2]或[12]。

借助标准符号特征标，我们可给出π-诱导的概念。

定义1设G为π-可分群且2∉π，如果H≤G，且θ∈Irr(H)为H的一个复特征标，记

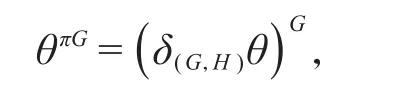
称之为θ到G的π-诱导。

本文采用一个简化记号。设(H，θ)和(K，ψ)均为G的特征标对且H≤G，如果ψ为θπK的一个不可约分量，我们记(H，θ)≤π(K，ψ)。使用特征标对的偏序关系，则等价于

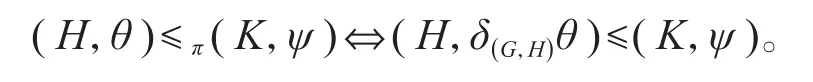
下述是π-诱导特征标的基本性质，本文将多次引用但不加说明。

引理1G设为π-可分群且2∉π，H≤G，θ∈Irr(H)且χ∈Irr(G)，则下述成立：

1）传递性：如果H≤K≤G，则(θπK)πG=θπG。

2）吸收性：θπGχ=(θχH)πG。

3）Mackey公式：如果K≤G使得G=HK，记D=H∩K，则(θπG)K=(θD)πK。

4）同一性：如果H⊲⊲G，则δ(G，H)=1H，从而θπG=θG，此时

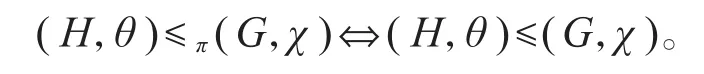
5）中介性：如果(H，θ)≤π(G，χ)，则对任意H≤K≤G，均存在ψ∈Irr(K)使得

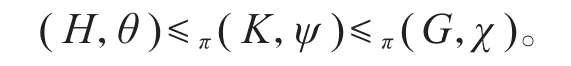
证明根据π-标准符号特征标的性质，可直接验证。或参考[16]中相关定理及证明。

下面是π-诱导的Clifford对应，本文将多次用到。

定理1设G为π-可分群且2∉π。如果N⊲G且θ∈Irr(N)，则特征标的π-诱导ξ↦ξπG定义了一个双射：Irr(Gθ|θ)→ Irr(G|θ)。

一般地，我们可将上述Clifford对应中的正规子群N替换为所谓的极大Fπ-对应，并证明其仍为诱导源（定义见[17]），本文称之为关于π-诱导的极大Fπ-对应。

定理2设G为π-可分群且2∉π，如果(S，η)、为G的一个极大次正规Fπ-对，令T=Gη，则特征标的π-诱导定义了一个双射

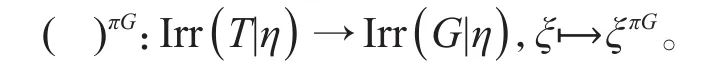
证明根据[2]中定理4.9，可知(S，η)为G的一个诱导源，即特征标的诱导

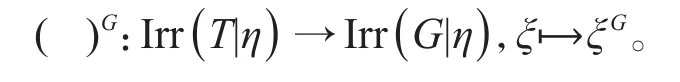
为双射。因为S⊲G，从π-标准符号特征标的性质（见[2]中引理 2.33（b））可得S＜Kerδ(K，T)。由此表明ξ↦δ(G，T)ξ给出了集合 Irr(T|η)到自身的一个双射，再与上述诱导双射合成，即得所证结论。

现在可给出Dπ-特征标的概念，具体背景和结论可见[18]。

定义2设G为π-可分群且2∉π，如果χ∈Irr(G)可从某个子群H的某个π-特殊特征标π-诱导，即存在H≤G及θ∈Xπ(H)使得χ=θπG，则称χ为G的一个Dπ-特征标。G的所有Dπ-特征标的集合记为Dπ(G)。

事实上，Dπ-特征标的概念是Dade在给Isaacs的一封信中首次提到的，作为Isaacs的Iπ-特征标的又一个典范提升，并证明了下述极为深刻的Dade定理，即[18]中的定理E。

定理3设G为π-可分群且2∉π，H≤G。如果θ∈Irr(H)满足θπG=χ∈Irr(G)，则χ∈Dπ(G)当且仅当θ∈Dπ(H)。

我们还需要Dπ-特征标的若干性质。

引理2设G为π-可分群且2∉π，则下述成立。

1）Xπ(G)=Dπ(G)∩ Fπ(G)。

2）Xπ(G)={χ∈Dπ(G)|χ(1)为π-数 }。

3）设χ∈Dπ(G)，H≤G，使得χH=θ∈Irr(H)，则θ∈Dπ(H)。进而，如果还有χ∈Xπ(G)，则θ∈Xπ(H)。

有了上述准备，现在给出Dπ-特征标的Dπ-原核概念。设χ∈Dπ(G)，其中G为π-可分群且2∉π。任取G的一个极大次正规的 Fπ-对(S，η)在(G，χ)的下方，令T=Gη，根据上述极大 Fπ-对应（即定理 2），存在唯一ξ∈Irr(T|η)的使得χ=ξπG，我们称(T，ξ)为(G，χ)的一个标准π-诱导对。根据 Fπ-特征标的性质（见[2]中4A），则(G，χ)的所有标准π-诱导对彼此共轭，即共轭唯一，并且(G，χ)=(T，ξ)当且仅当χ为 Fπ-特征标。

重复上述选取标准π-诱导对的过程：即任取(G，χ)的一个极大 Fπ-对(S1，η1)，得到第一个标准π-诱导对：

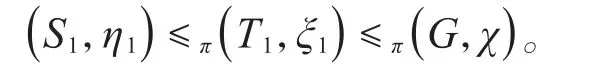
再任取(T1，ξ1)的一个极大 Fπ-对，又得到第二个标准π-诱导对：(S2，η2)≤π(T2，ξ2)≤π(T1，ξ1)。值得注意的是，虽然(S1，η1)是T1的一个 Fπ-对，但却未必是T1的极大Fπ-对，因为T1一般来说仅仅是G的子群，故T1的次正规子群在G中未必正规。现在(S2，η2)是T1的一个极大 Fπ-对，故(S1，η1)包含在(S2，η2)的某个T1-共轭中。不断重复上述过程，直到某个标准π-诱导对中出现Fπ-特征标，此时该过程自动结束。据此我们就得到了(G，χ)的一个标准π-诱导对序列：(G，χ)=(T0，ξ0)＞ (T1，ξ1)＞…＞ (Tk，ξk)，其中每一项均是前一项的一个标准π-诱导对，并且只有最后一项的ξk才是 Fπ-特征标。不难看出(G，χ)的标准π-诱导对序列也是共轭唯一的，我们称(Tk，ξk)为χ的一个Dπ-原核，简称为原核。

以下是Dπ-原核的简单性质。

引理3设G为π-可分群且2∉π，如果(W，γ)为χ∈Dπ(G)的一个原核，则下述成立。

1）γ∈ Xπ(W)且γπG=χ。

2）(W，γ)是共轭唯一的。

3）χ∈Fπ(G)当且仅当(W，γ)=(G，χ)。

4）如果(S，η)≤(G，χ)为的一个极大 Fπ-对，则(S，η)做适当的共轭替换后，可设(S，η)≤(W，γ)。

5）如果(T，ξ)为χ的一个π-标准诱导对，则ξ的每个原核均与(W，γ)在G中共轭。

2 主要结果及证明

我们先证明本文的定理B，方便起见，重述如下。

定理4设G为π-可分群，2∉π，并且α∈Xπ(H)使得απG。如果J≤G，且 |H：H∩J|为一个π'-数，则(αH∩J)πG∈ Irr(G)。

证明因为α∈Xπ(H)也是Dπ-特征标，并且απG不可约，从定理 2 可知απG也是Dπ-特征标，从而φ=(απG)0∈Iπ(G)，并且φ=(α0)G。注意到α0∈Iπ(H)具 有π-次 数α(1)，根 据[13]中 定 理 3.1，则（(α0)H∩J)J∈Iπ(J)。不难看出

故(αH∩J)πJ必然是不可约的。

借助定理B，我们可证下述本文的定理A。

定理5设G为π-可分群且2∉π，H是G的子群 且α∈Xπ(H)。 如 果απG是 不 可 约 的 ，任 取β∈ Xπ′(H)，则(αβ)πG也是不可约的。

证明我们将使用归纳法进行证明，首先对|G|归纳，再对|G：H|进行归纳。因为H=G时结论显然成立，故不妨设H＜G。

设L=CoreG(H)，选 取v∈Irr(L)在α下 方 ，θ∈Irr(L)在β下方，则v是π-特殊的，而θ是π'-特殊的。再设Gν为ν在G中的稳定子，而Gθ为θ在中G的稳定子，由π-诱导的Clifford对应，则存在ξ∈Irr(Hv|v)和τ∈Irr(Hθ|θ)使得ξπH=α且τπH=β。由于α(1)为π-数，β(1)为π'-数，故|H：Hv|为π-数，而|H：Hθ|为π'-数 ，据 此 可 知H=HvHθ。 再 令D=Hv∩Hθ，相关子群和特征标如图1所示。

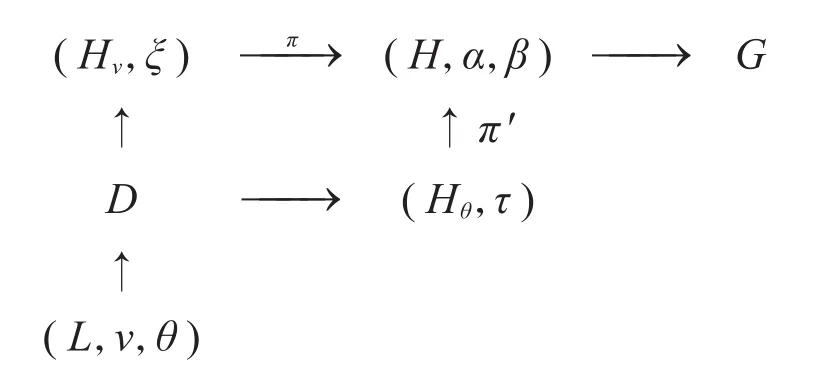
图1 子群和特征标Fig.1 Subgroups and characters

因为G为π-可分群，2∉π，根据[2]中推论2.38，从α是π-特殊的，可知ξ也是π-特殊的。又因为2∈π'，故π-标准符号特征标δ(H，Hθ)总是π'-特殊的，现在τπH=β，即（δ(H，Hθ)τ）H=β，仍从[2]中推论2.38可知δ(H，Hθ)τ也是π'-特殊的，迫使τ也是π'-特殊的。在使用Gajendragadkar限制定理（即[2]中定理2.10），从|Hv：D|=|H：Hθ|为π'-数，且|Hθ：D|=|H：Hv|为π-数，可知ξD∈ Xπ(D)且τD∈ Xπ′(D)。我们有

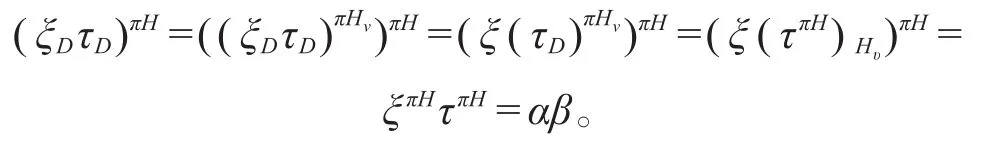
注意到ξπG=(ξπH)πG=απG，按假设不可约，故ξπGυ也不可约。简单计，令J=G(v，θ)=Gv∩Gθ，我们有Hv∩J=Hv∩ (Gv∩Gθ)=D，故 |Hv：Hv∩J|=|Hv：D|为π-数，即图2特征标图表恰为定理B的环境：所以(ξD)πJ不可约。

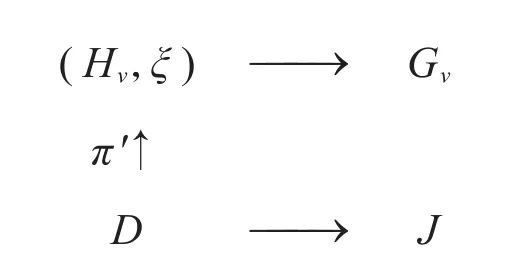
图2 特征标Fig.2 Characters

如果J＜G，即|J|＜|G|，由于τD∈Xπ'(D)，故由归纳假设，则 (ξDτD)πJ不可约。根据 Gajendragakar乘积定理（见[2]中定理2.2），可知J=Gv∩Gθ=Gvθ恰为正规子群L的不可约特征标vθ在G中的稳定子，而ξDτD显然在vθ上方，从而(ξDτD)πJ也在vθ上方，再使 用π-诱导的Clifford 对应 ，则 ((ξDτD)πJ)πG=(ξDτD)πG也不可约，等价于(αβ)πG也是不可约的，故所证结论成立。因此，我们以下可假设J=G，即v和θ都是G-不变的。

因为L⊲G且l≤H＜G，故存在G的一个主因子K/L。记U=KH且V=K∩H。由于G为π-可分群，故主因子K/L或者为π-群，或者为π'-群。以下分两种情形讨论。

先假设K/L为π'-群，因为α∈Xπ(H)，并且从已知条件απG不可约，推出απU也不可约，再从 Dade定理得到απU∈Xπ(U)。任取η∈Irr(K)在απU的下方，则η∈Dπ(K)。由于v∈Xπ(L)在α∈Irr(H)的下方，并且v为G-不变的，故v也在η的下方。进而，从K/L为π'-群，可知v在K上存在典范扩张，根据Gallagher对应，则η=σ，其中σ∈Irr(KL)=Xπ′(K/L)，表明η为Fπ-特征标，故η∈Dπ(K)∩Fπ(K)=Xπ(K)。此时，再使用Gajendragadkar限制定理，则ηL=v，并且η和v相互唯一确定，导致η也是G-不变的。但ηV也不可约，我们有限制对应：Irr(U|η)→ Irr(H|ηV)。显然α也在ηV的上方，故α也可扩张到U上，与απU不可约矛盾，表明该情形不能发生。

再假设K/L为π-群，类似上段证明，因为θ∈Xπ′(L)且为G-不变的，故存在典范扩张∈ Xπ′(K)。仍从θ的G-不变性，推出也是G-不变的。又因为V⊲H，则V必然是H-不变的，可令βV=eδ，其中δ∈Xπ′(V)必然也在θ的上方，迫使β也只能

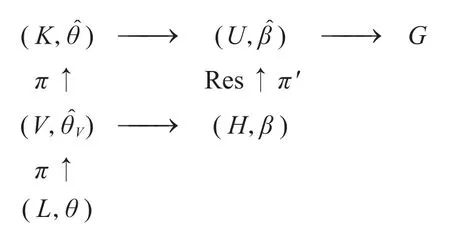
图3 限制对应Fig.3 Restriction Correspondence

既然β∈Xπ′(H)可扩张到U上，必然存在一个扩张β∈ Xπ′(H)。此时β'在的上方，故β'在K上的某个不可约分量θ'（自动是 Xπ′-特征标）也在的上方，根据 Gajendragadkar限制定理，迫使，从而。

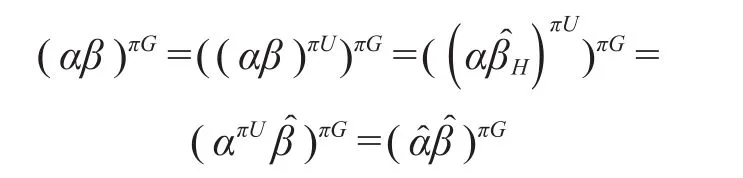
也不可约，至此完成证明。

最后我们将证明比本文定理C稍加一般化的结论。

定理6设G为π-可分群且2∉π，(Wi，γi)是χi∈Dπ(G)的一个原核，并且δi∈Xπ'(Wi)，其中i=1，2。 如果(γ1δ1)πG=(γ2δ2)πG，则存在x∈G使得(W1，γ1δ1)x=(W2，γ2δ2)。特别地，有χ1=χ2。

证明根据原核的构造定义，可取G的一个极大 Fπ-对 (Si，θi)≤(Wi，γi)，使得(Wi，γi)为的 一 个原核，其中Ii=Gθi，并且，此时

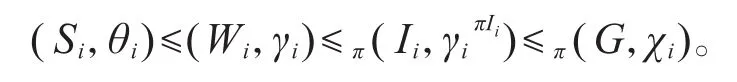
再任取βi∈Irr(Si) 使得(Si，βi)≤(Wi，δi)，令χ=(γ1δ1)πG=(γ2δ2)πG，则(Si，θiβi)均为χ下方的极大 Fπ-对，故存在x∈G使得

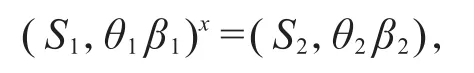
即θ1x=θ1，β1x=β1，以及S1x=S2。如果I2=G，则S2=G=S1，此时W1=W2=G，结论自然成立，以下不妨设I2＜G。

根据π-标准符号特征标的定义

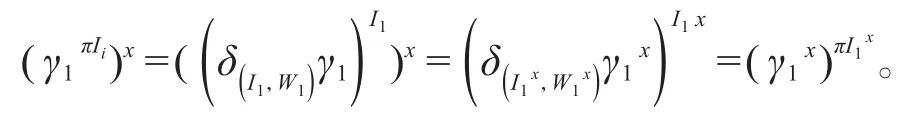
上述已证θ1x=θ1且S1x=S2，按定义有

所以

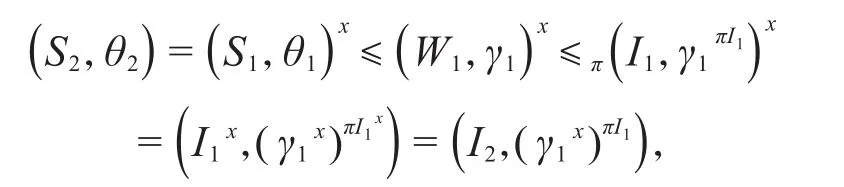
并且(W1x，γ1x)也是的一个原核。又因为

令T=G(θ2β2)=Gθ2∩Gβ2，则S2⊆T⊆I2显然成立，故存在v1∈Irr(T)使得

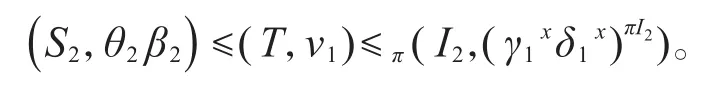
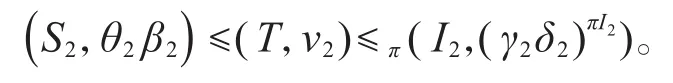
再由极大Fπ-对应定理可知viπG均不可约，故，从而

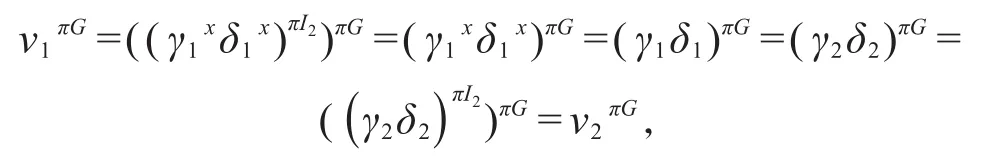
仍从极大Fπ-对应可知v1=v2，于是(γ1xδ1x)πI2=(γ2δ2)πI2。注意到|I2|＜|G|，我们对 |G|作归纳法，使用归纳假设即知存在某个元素y∈I2，使得，亦即

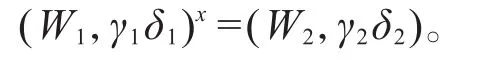
特别地，我们有

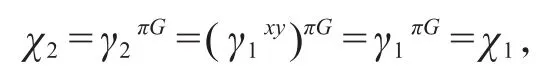
至此完成所证。作为应用，可直接得到下述本文定理C。

推论 1设G为π-可分群且2∉π，(W，γ)是χ∈Dπ(G)的一个原核。如果δ1，δ2∈Xπ'(W)使得(γδ1)πG=(γδ2)πG，则δ1=δ2。

证明根据上述定理，存在x∈G使得(W，γδ1)x=(W，γδ2)。 所以x∈NG(W)且γx=γ以 及δ1x=δ2。按定义γπG=χ不可约。从而也不可约，但x固定γ不变，只有x∈W。由此即得δ1=δ1x=δ2。