圆助攻,巧解三角形最值问题

广东省佛山市第四中学(528000) 黄 仪

解三角形中的最值问题,一般是利用正余弦定理,结合基本不等式,或三角函数的有界性,二次函数的最值等方法求解,但通常会推导过程繁冗,计算量大,容易出错,尤其是选择填空题,做题耗时过多,得不偿失.三角形中角度和边长的变化,其实就是平面几何中点和线的变化,能否跳出知识的局限,利用平面几何辅助解题? 平面几何中的圆,由于其半径和圆心角,圆周角的特性,往往成为一个很好的解题助力工具.

一、角的转化

三角形中,当点动而角不变时,如果定角所对的边也是定值,求最值问题时,可将角转化为同圆中同弧所对的圆周角或圆心角, 利用同弧所对的圆周角或圆心角不变的性质,化动为静.

例1(2014 高考新课标Ⅰ卷理科) 已知a,b,c分别为ΔABC的三个内角A,B,C的对边,a= 2 且(2 +b)(sⅰnA −sⅰnB) = (c −b)sⅰnC, 则ΔABC的面积的最大值为____.

解由正弦定理, (2 +b)(sⅰnA−sⅰnB)=(c−b)sⅰnC即(2+b)(a−b)=c(c−b),将a=2代入整理得b2+c2−a2=bc,所以cosA=边a为定长2,角A为定值, 构造ΔABC外接圆O, 则点A可看作圆O中所对的圆周角∠BAC的顶点,由垂径定理易知当AO⊥BC时,ΔABC的面积最大,为

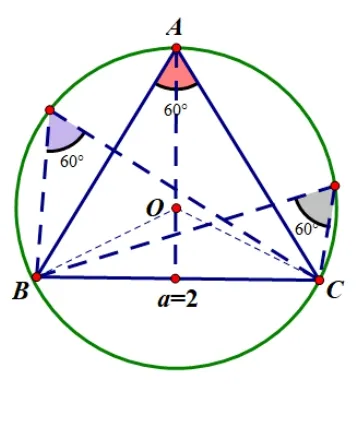
图1

评析这是一道求面积最值的经典题目,方法多样.构造圆,利用几何辅助解题是最灵活,计算量最少的解法.通过角度不变,点A可看作在圆周上运动,角A两边长的变化转化为三角形高的变化,求面积的最值即求高的最值.

例2ΔABC中, ∠ABC= 90°,AC= 2BC=P是ΔABC内一动点,∠BPC= 120°,则AP的最小值为____.

解以BC为x轴,BA为y轴建立平面直角坐标系, 构造圆O, 使BC为圆O的弦, ∠BPC为优弧BC所对的圆周角恒为120°, 则点P的运动轨迹为弧BC.线段AP的最小值就转化为点A到弧BC的距离的最小值.由BC=圆心角∠BOC= 120°易知O点坐标为, 圆O半径为2, 则AP的最小值=|OA|−|OP|=

图2

评析此处巧妙地用了平面几何与解析几何中圆的性质.首先由动点P形成的角为定值,将点动转化为角动,根据角度不变构造出同弧所对的圆周角,再将AP的值转化为点到圆的位置关系求解,利用坐标系大大简化了计算量.

二、边的转化

三角形中,点动,角变,而边不变,结合圆中的定长为半径或直径,可将三角形中的一条动边构造为圆的半径或直径,将点动转化为圆中半径位置的转动,进而引起其他顶点或角度的变化,再结合圆的性质,求出相应的取值范围.

例3在ΔABC中,AB= 1,BC= 2,求角C的取值范围.

解以B为圆心,AB= 1 为半径构造半圆, 当顶点A从点M沿着半圆弧运动到点N的过程中, 角C从零开始, 先逐渐增大,当CA与半圆B相切时,角C最大,为30°,然后又逐渐减小至零,得出角C的取值范围是(0,30°].

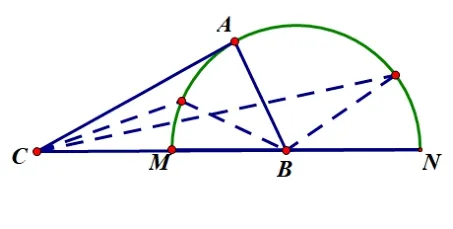
图3

评析本题中角C的对边为定值,以定长为半径构造圆,当角C变化时,点A在半圆周上运动,角C的值随着角A的变化而变化,由角A的取值范围得出角C的取值范围.这一招可谓“动中求变化,变中有方法”!

三、三角形的转化

平面四边形中,某动点在变化,带动其它的点也在对应变化(这两个称之为对应点),相当于整个图形在变化,其中蕴含着变化的三角形与不变的对应关系,将其中变化的三角形构造圆,对应点利用其对应关系也构造出相应的圆,两圆相结合辅助解题,事半功倍.

例4在平面四边形ABCD中,AD= 2,CD= 4,ΔABC为正三角形,则ΔBCD面积的最大值为____.

图4

解以点C为原点,CD为x轴建立平面直角坐标系, 则D(4,0), 由AD= 2,CD= 4 可知点A在圆D: (x −4)2+y2= 4 上, 因为是点A绕原点C旋转60°得到点B,所以点A的轨迹圆D绕原点C逆时针旋转60°所得点B的轨迹圆E,可求得所以点B(x,y)在圆E: (x −2)2+= 4 上,易知|y|≤所以有ymax=所以ΔBCD面积的最大值为

评析本题中点A,C在变化,带动点B也在动,其不变关系是等边ΔABC.构造出动点A作圆周运动的圆D,再根据等边三角形中的定角∠ACB及等边,得出动点B的运动轨迹圆E,相当于把ΔACD旋转到ΔBCE,动点B的的运动过程,就是ΔBCD高的变化过程,从而确定面积的变化.本题是“点(A)动——点(B)动——线(高)动”的变化过程,构思巧妙,技巧性强.

例5如图5 在凸四边形ABCD中,AB=1,BC=√AC⊥CD,AC=CD,当∠ABC变化时,对角线BD的最大值为____.

解以B为圆心,AB半径构造圆B,以C为圆心,将圆B旋转90°得到圆E,则∠BCE= 90°,BC=CE=BE=当点A在圆B上运动时,点D在以E为圆心,1为半径的半圆上运动,由图得BD的最大值即BE的长加圆E的半径,即√

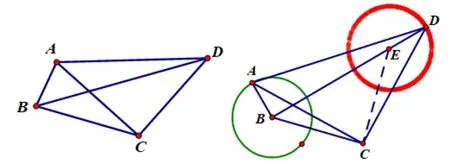
图5

评析本题与例4 异曲同工,也是构造双圆辅助解题.将ΔABC旋转变换到ΔDEC,即圆B变换到圆E,即利用点A的运动轨迹求出点D的运动轨迹,此时,即可眼前一亮,豁然开朗,进而结合圆的性质解出此题.

三角形的转化,其实就是边和角的转化,归根到底还是根据点的运动、点和线的变化,把点、线的运动与圆相结合,构造圆解题.借助圆这个工具,解题跳出知识的局限,回归平面几何与解析几何的本质时,则可以从几何要素点、线、角、三角形等角度,将问题转化为观察变化规律的几何问题,避免大量的三角运算,缩短解题时间,化繁为简.

在教学中,要求学生有较强的抽象思维能力以及平面几何,空间几何的想象能力,平时多观察,多思,多练,多画(图),跳出思维的框架,发挥想象的空间;还要善于将知识点融会贯通,综合运用,将三角函数与平面几何、解析几何综合运用,灵活转换,学生要有扎实的数学基础和培养良好的数学素养;最后要有模型意识,善于建立数学模型.与圆相结合的解三角形问题具有较高的特定性和技巧性,需要在实际解题过程中多体会模型的特征,提高解三角形问题的几何意识.