利用“齐次化法”求多元函数最值问题

北京市日坛中学(100020) 李妍华 徐小花 王树文

2020年高考、强基、竞赛中多元函数最值问题高频出现,多元函数问题形式复杂,解法灵活,能有效考察学生转化构造创新的能力.多元函数最值问题我们常用消元、重要不等式、三角换元等方法完成.“齐次化法”也是解答多元函数最值问题的常见策略之一, 此法有其普适性和广泛的应用性,笔者以2020年几个考题为例,将其“齐次化法”求解与读者交流.

例1(2020年北大强基计划第9 题)使得5x+a(x+y)对所有正实数x,y都成立的实数a的最小值为( )

A.8 B.9 C.10 D.前三个答案都不对

解析由于x,y为正实数,且5x+≤a(x+y),参变分离得√

设f=则fmax≤a.因此将问题转化为求二元函数最大值问题.对f进行变形,得f=设=t,(t ＞0),则f=于是,我们可以利用Δ 判断法求f的最大值.

由f的表达式得到: (5−f)t+−f= 0.我们可以把该式看成是一个关于的一个一元二次方程.由Δ ≥0,得122+4(5−f)f≥0,得f2−5f −36 ≤0,解得−4 ≤f≤9.因为t ＞0,f ＞0,所以0＜f≤9.当t=时(满足t ＞0),f取得最大值9.故选B.

点评参变分离是求参数取值范围的有效方法也是常规方法.本题困难的地方是参变分离后对二元函数求最大值.在本文我们利用“齐次化法”巧妙地将两个变量x,y整合为一个新变量将二元函数最大值问题转化为一元函数最大值问题,再利用Δ 判断法求得f的最大值为9,问题得到圆满解决.

例2(2020年复旦大学自主招生第2 题)已知实数x、y,满足x2+2xy −1=0,求x2+y2的最小值.

解析因为x2+2xy −1=0,所以x2+2xy=1,依题

点评“齐次化法”往往适用于分式结构,高中生比较熟悉的是此法在三角函数中的应用,例如: 已知tanα= 2,求的值.在本题中x2+y2是一个整式,先要对式子进行恒等变形转化成分式结构再“齐次化”,最后应用基本不等式、Δ 判定、换元求导方法快速解答.在这里我们给出的是利用基本不等式解答,读者也可以试一试Δ 判定、换元求导方法.

例3(2020年高考江苏卷第12 题)已知5x2y2+y4=1(x,y ∈R),则x2+y2的最小值是____.

解析设f=x2+y2,则

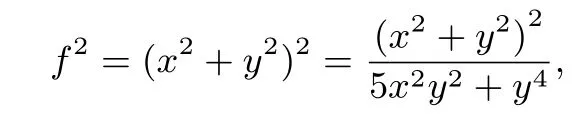
又

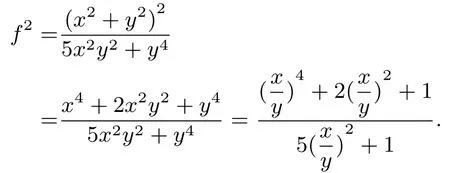
点评例3 和例2 有相同的地方也有区别,都可以将整式利用除“1”(在例2 中1=x2+2xy,例3 中1=5x2y2+y4)转化为分式, 但是例3 不能直接除“1”.这也是使用“齐次化法”需要注意的另外一个点, 分子分母次数要一致.分子f=x2+y2是二次齐次式,分母5x2y2+y4是四次齐次式,要想次数一致,首先要对分子进行平方.这种转化齐次式的构造方法,看似形式变复杂,实则巧妙地找到了解题途径,可谓独具匠心.

例4(2020年全国高中数学联赛(四川预赛)第6 题)已知正实数x,y满足:= 1,则x+y的最小值是____.

解析依题

设x+3y=m,2x+y=n,则x+y=所以

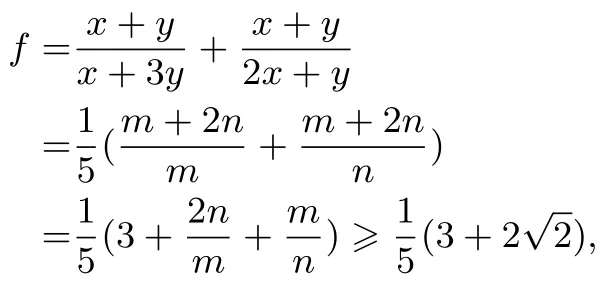
点评齐次转化、分母置换后,将其转化为应用不等式求最值的目标形式快速获解.由上述例题知,齐次“降元”转化改变函数结构后,易找到解题途径.

例5(2020年全国高中数学联赛(甘肃赛区)预赛第2题)设x,y均为正数,则的最小值为____.

解析设x+3y=m,则

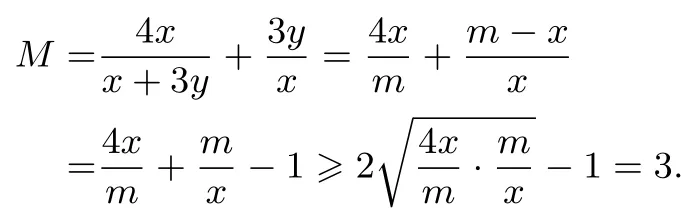
评析例5 的解法和例4 如出一辙,都利用到了将分母“简化”巧妙地将其转化为应用不等式求最值的目标形式快速获解.

许多重要不等式如基本不等式、柯西不等式自身就是齐次不等式,所以证明一些带条件的非齐次不等式时,利用所给条件对原不等式的结论进行恒等变形,转化为齐次不等式,最终化为易于证明的形式.