抛物线中两条垂直的焦点弦的几个优美结论

南京市栖霞中学(210046) 刘建国

近期,笔者整理有关圆锥曲线焦点弦的问题时,拜读文[1]后通过类比联想,将椭圆的有关两条垂直焦点弦的问题推广到抛物线中,得出了一系列结论,并对其进行整理.

结论1已知AB、CD是抛物线E:y2= 2px(p ＞0)中经过焦点F的两条相互垂直的弦, 抛物线在A,B两点处的切线交于点Q, 则直线CD必过Q点.

图1

证明如图1 所示: 设A(x1,y1)、B(x2,y2)(其中y1＜0,y2＞0),则A,B两点的坐标满足

x2=设直线AB的方程为:y=则直线CD的方程为:y=;在x轴上方所对应的抛物线方程为:y=则y′=在x轴下方所对应的抛物线方程为:y=−则y′=−则在A点的切线方程为:lA:y−y1=(x−x1),将①代入化简可得:lA:y=同理可得:B处的切线方程为:lB:y=将lA、lB联立的:解得:即将直线AB与抛物线E联立得:整理得:k2x2−(pk2+2p)x+=0,根据韦达定理可知:

将③代入Q点坐标得则点Q满足直线CD的方程,所以直线CD必过Q点.

结论2已知AB、CD是抛物线E:y2= 2px(p ＞0)中经过焦点F的两条相互垂直的弦, 抛物线在A,B两点处的切线交于点Q, 令s=则s+t=2u.

图2

证明如图2 所示, 设直线CD的方程为:y=C(x1,y1)、D(x2,y2),由结论1 可知:且C,D,Q三点共线, 所以:|QF|−|QC|=|CF|,|QD|−|QF|=|DF|,则:

同理可得:

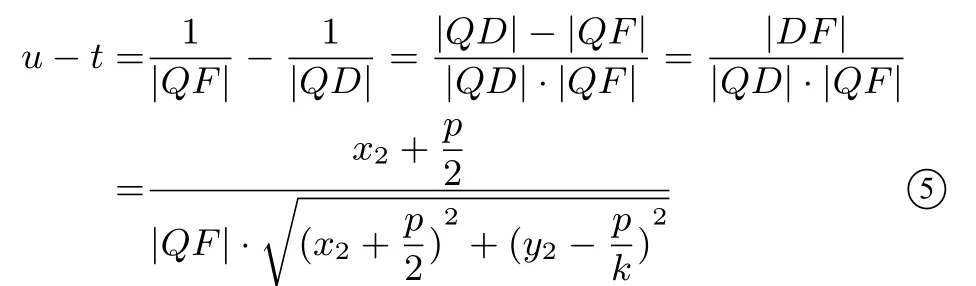
因为C,D满足直线CD的方程, 所以:y1=且将y1、y2代入④⑤可得:s −u=u −t=所 以s −u=u −t,即s+t=2u.

结论3已知AB、CD是抛物线E:y2=2px(p ＞0)中经过焦点F的两条相互垂直的弦,则(即为定值).

证明如图3,设A(x1,y1)、B(x2,y2)(其中y1＜0,y2＞0), 直线AB的方程为:因为AB⊥CD,则直线CD的方程为:y=所以|AB|=将②代入得:

图3

结论4已知AB、CD是抛物线E:y2= 2px(p ＞0)中过焦点F的两条相互垂直的弦,M、N分别是AB、CD的中点,则直线MN恒过定点

证明如图4, 设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4), 直线AB的方程为:y=k(x −则直线CD的方程为:y=由中点坐标公式得:由结论1 的证明中②式和③式可知:将直线CD与抛物线E联立得:整理得:x2−(p+2pk2)x+

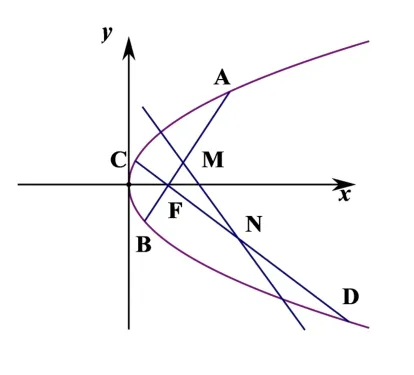
图4

根据韦达定理可得:x3+x4=p+2pk2,所以y3+y4=(x3+x4−p)=−2pk,所以当直线MN的斜率不存在时, 满足:所以k=±1, 直此时直线MN的方程为:直线MN过定点当直线MN的斜率存在时, 即:k /=±1, 由M,N两点的坐标可知直线MN的方程为:y+pk=化简得:即直线MN过定点综上所述:直线MN恒过定点

结论5已知AB、CD是抛物线E:y2= 2px(p ＞0)中过焦点F的两条相互垂直的弦,|AB|+|CD|存在最小值,且最小值为8p.

证明由结论3 的证明中⑥式可知:|AB|+|CD|=+2p(1+k2) = 4p+2p(k2+) ≥4p+2p×= 8p(当且仅当k=±1 时等式成立), 所以|AB|+|CD|的最小值为8p.

结论6已知AB、CD是抛物线E:y2= 2px(p ＞0)中过焦点F的两条相互垂直的弦, 则四边形ACBD的面积的最小值为8p2.

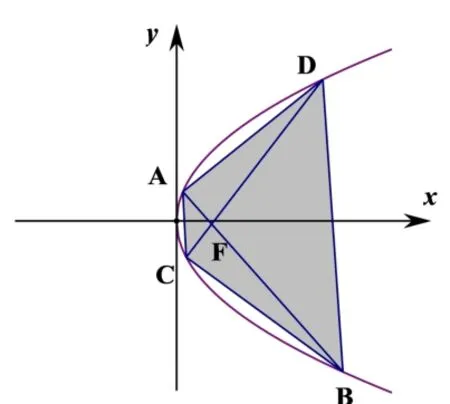
图5

证明如图5,因为AB⊥CD,由结论3 的证明中⑥式可知四边形ACBD的面积为:

(当且仅当k=±1 时等式成立),所以四边形ACBD的面积的最小值为8p2.