函数拐点偏移问题的探究

广东省中山纪念中学(528454) 邓启龙

函数极值点偏移问题是近几年高考的热点,也是高考复习中的重点和难点.类似地,函数也存在拐点偏移,处理极值点偏移和拐点偏移问题,有一些成熟有效的方法,比如构造对称函数、利用对数平均不等式等.文[1]通过对函数极值点偏移问题的本质进行探究,得到了处理函数极值点偏移问题的一种新方法.众所周知,函数的拐点也是导函数的极值点,那么函数的拐点偏移和导函数的极值点偏移之间有什么联系呢? 本文通过探究,得到了函数的拐点偏移和导函数的极值点偏移之间的关系.

1 极值点偏移

已知函数y=f(x)在(a,b)上连续,且在(a,b)内只有一个极值点x0.

定义1若对任意满足f(x1) =f(x2), 且a ＜x1＜x2＜b的x1,x2,都有x0＜则函数f(x)在(a,b)上极值点x0左偏;

定义2若对任意满足f(x1) =f(x2), 且a ＜x1＜x2＜b的x1,x2,都有x0＞则函数f(x)在(a,b)上极值点x0右偏.

2 拐点偏移

已知函数y=f(x)在(a,b)上连续,且在(a,b)内只有一个拐点x0.

定义3若对任意满足f(x1) +f(x2) = 2f(x0), 且a ＜x1＜x2＜b的x1,x2,都有x0＜则函数f(x)在(a,b)上拐点x0左偏;

定义4若对任意满足f(x1) +f(x2) = 2f(x0), 且a ＜x1＜x2＜b的x1,x2,都有x0＞则函数f(x)在(a,b)上拐点x0右偏.

3 深入探究

已知函数f(x)在(a,b)上单调递增且只有一个拐点x0,当x ∈(a,x0)时,f′′(x)＜0,当x ∈(x0,b)时,f′′(x)＞0,即函数f(x)在(a,b)内先上凸后下凸.函数f(x)的拐点x0也是导函数f′(x)的极值点,于是f′(x)在(a,b)上先递减后递增,且只有一个极值点x0.若f′(x)在(a,b)上极值点x0右偏,从直观图象上看,f′(x)的函数图象在x0右边部分比左边部分更陡峭, 即f′(x) 在(x0,b) 上比在(a,x0) 上变化快.因为f′(x)是f(x)函数图象上点的切线斜率,所以f(x)函数图象上点的切线斜率的变化速度越来越快,函数图象在x0右边部分比左边部分更陡峭,于是f(x)拐点x0右偏.若f′(x)在(a,b)上极值点x0左偏,同理可推出f(x)拐点x0左偏.

但是以上推导不能代替证明,笔者经过深入探究,得到以下定理并严格证明.

定理1已知函数f(x) 在(a,b) 上单调递增且只有一个拐点x0, 当x ∈(a,x0)时,f′′(x)＜0, 当x ∈(x0,b)时,f′′(x)＞0.若f′(x) 在(a,b) 上极值点x0右偏(左偏), 则f(x)在(a,b)上拐点x0右偏(左偏).

证 明设g(x) =f(x) +f(2x0−x), 则g′(x) =f′(x)−f′(2x0−x).

若f′(x) 在(a,b) 上极值点x0右偏, 则对任意满足f′(x1) =f′(x2), 且a ＜ x1＜ x2＜ b的x1,x2, 都有x0＞即2x0−x1＞x2＞x0.由f′(x)在(x0,b)上单调递增得f′(2x0−x1)＞ f′(x2) =f′(x1), 于 是f′(x1)−f′(2x0−x1)＜0.所以当x ∈(a,x0)时,g′(x)＜0,g(x) 在(a,x0) 上单调递减.同理可得g(x) 在(x0,b) 上单调递增.于是当x ∈(a,b) 且x /=x0时,g(x)＞g(x0), 即f(x)+f(2x0−x)＞2f(x0).

对任意满足f(x1) +f(x2) = 2f(x0), 且a ＜x1＜x2＜b的x1,x2, 有f(x1)+f(2x0−x1)＞2f(x0), 于是f(2x0−x1)＞2f(x0)−f(x1) =f(x2).因为f(x)在(a,b)上单调递增,所以2x0−x1＞x2,即x0＞则函数f(x)在(a,b)上拐点x0右偏.

若f′(x)在(a,b)上极值点x0左偏, 同理可得f(x)在(a,b)上拐点x0左偏.

定理1 给出了在(a,b)内先上凸后下凸的单调递增函数f(x)的拐点偏移情况的判定方法,若单调递增(减)函数f(x)在(a,b)内先下凸(上凸)后上凸(下凸),类似地,有以下定理(证明略):

定理2已知函数f(x) 在(a,b) 上单调递增且只有一个拐点x0, 当x ∈(a,x0)时,f′′(x)＞0, 当x ∈(x0,b)时,f′′(x)＜0.若f′(x) 在(a,b) 上极值点x0右偏(左偏), 则f(x)在(a,b)上拐点x0左偏(右偏).

定理3已知函数f(x) 在(a,b) 上单调递减且只有一个拐点x0, 当x ∈(a,x0)时,f′′(x)＞0, 当x ∈(x0,b)时,f′′(x)＜0.若f′(x) 在(a,b) 上极值点x0右偏(左偏), 则f(x)在(a,b)上拐点x0右偏(左偏).

定理4已知函数f(x) 在(a,b) 上单调递减且只有一个拐点x0, 当x ∈(a,x0)时,f′′(x)＜0, 当x ∈(x0,b)时,f′′(x)＞0.若f′(x) 在(a,b) 上极值点x0右偏(左偏), 则f(x)在(a,b)上拐点x0左偏(右偏).

文[1]通过对函数极值点偏移问题的本质进行探究,得到了判定函数极值点偏移的非常有效的方法.由于函数的拐点偏移和导函数的极值点偏移存在以上关系,于是可以得到判定函数拐点偏移的以下定理:

定理5已知函数f(x) 在(a,b) 上单调递增且只有一个拐点x0, 在(a,x0) 和(x0,b) 上f′′(x) 异号.若任意x ∈(a,b),f(4)(x)＞0(＜0)恒成立,则f(x)在(a,b)上拐点x0右偏(左偏).

证明1.若当x ∈(a,x0)时,f′′(x)＜0,当x ∈(x0,b)时,f′′(x)＞0, 则f′(x) 在(a,b) 内只有一个极值点x0, 当x ∈(a,x0)时,(f′(x))′ ＜0,当x ∈(x0,b)时,(f′(x))′ ＞0.由文[1]的定理1 得若任意x ∈(a,b),f(4)(x)＞0(＜0)恒成立,则f′(x)在(a,b)上极值点x0右偏(左偏).由本文的定理1 得f(x)在(a,b)上拐点x0右偏(左偏).

2.若当x ∈(a,x0) 时,f′′(x)＞0, 当x ∈(x0,b) 时,f′′(x)＜0, 则f′(x) 在(a,b) 内只有一个极值点x0, 当x ∈(a,x0)时,(f′(x))′ ＞0,当x ∈(x0,b)时,(f′(x))′ ＜0.由文[1]的定理2 得若任意x ∈(a,b),f(4)(x)＞0(＜0)恒成立,则f′(x)在(a,b)上极值点x0左偏(右偏).由本文的定理2 得f(x)在(a,b)上拐点x0右偏(左偏).

定理5 表明,对于单调递增函数,无论是先上凸后下凸还是先下凸后上凸,若f(4)(x)恒正(负),则拐点x0右偏(左偏).对于单调递减函数,类似地,有以下定理(证明略):

定理6已知函数f(x) 在(a,b) 上单调递减且只有一个拐点x0, 在(a,x0) 和(x0,b) 上f′′(x) 异号.若任意x ∈(a,b),f(4)(x)＞0(＜0)恒成立,则f(x)在(a,b)上拐点x0左偏(右偏).

4 典型例题

下面给出几个典型的函数拐点偏移问题,并结合本文的定理加以分析.

例1已知函数f(x) = ex −若x1/=x2, 且f(x1)+f(x2)=2,证明:x1+x2＜0.

证明易得f′(x) = ex −x ＞0 对任意x ∈R 恒成立,所以f(x)在R 上单调递增.由f′′(x) = ex −1 得f(x)在R 上只有一个拐点0, 且f′′(x) 在(−∞,0) 和(0,+∞)上异号.因为f′′′(x) = ex,f(4)(x) = ex, 所以任意x ∈R,f(4)(x)＞0 恒成立.由定理5 得f(x)在R 上拐点右偏,又f(x1)+f(x2)=2f(0),于是0＞得x1+x2＜0.

例2已知函数f(x) =x2+2 lnx+x,0＜x1＜x2且f(x1)+f(x2)=4.证明:x1+x2＞2.

证明易得f′(x)=2x++1＞0 对任意x ＞0 恒成立,所以f(x)在(0,+∞)上单调递增.由f′′(x)=得f(x)在(0,+∞)上只有一个拐点1,且f′′(x)在(0,1)和(1,+∞)上异号.因为f′′′(x) =所以任意x ＞0,f(4)(x)＜0 恒成立.由定理5 得f(x)在(0,+∞)上拐点左偏,又f(x1)+f(x2) = 2f(1),于是1＜得x1+x2＞2.

例3已知函数f(x) =x+−x2, 0＜x1＜x2且f(x1)+f(x2)=2.证明:x1+x2＞2.

证明易得

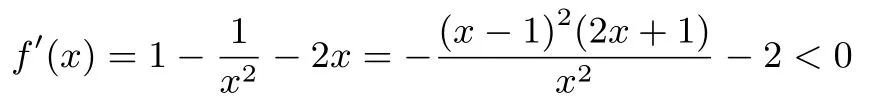
对任意x ＞0 恒成立,所以f(x)在(0,+∞)上单调递减.由f′′(x) =−2 得f(x)在(0,+∞)上只有一个拐点1,且f′′(x)在(0,1)和(1,+∞)上异号.因为

所以任意x ＞0,f(4)(x)＞0 恒成立.由定理6 得f(x)在(0,+∞) 上拐点左偏, 又f(x1) +f(x2) = 2f(1), 于是得x1+x2＞2.

例4已知函数f(x) =x2lnx −0＜x1＜x2＜e且f(x1)+f(x2)=−3.证明:x1+x2＜2.

证明易得f′(x) = 2xlnx −2x= 2x(lnx −1)＜0 对任意x ∈(0,e)恒成立, 所以f(x)在(0,e)上单调递减.由f′′(x) = 2 lnx得f(x)在(0,e)上只有一个拐点1,且f′′(x)在(0,1)和(1,e)上异号.因为f′′′(x) =所以任意x ∈(0,e),f(4)(x)＜0 恒成立.由定理6 得f(x) 在(0,e) 上拐点右偏, 又f(x1) +f(x2) = 2f(1), 于是1＞得x1+x2＜2.

函数极值点偏移和拐点偏移问题是考查导数的常见的题型,本文通过探究函数拐点偏移和导函数极值点偏移的内在联系,得到了判定函数拐点偏移的非常有效的方法.