“问题·账户·系统”学习法*

2021-04-21山东省实验中学250109张蕴禄

中学数学研究(广东) 2021年5期

山东省实验中学(250109) 张蕴禄

“让学生学会学习”是世界各国课程改革的永恒主题.“教会学生学习”已成为当今世界流行的口号.我国著名教育家陶行知先生早就指出:“我以为好的先生不是教书,不是教学生,乃是教学生学.”数学课程改革的一个显著特点就是要求关注学生的发展,激发学生学习数学的兴趣,促进学生数学学习行为和习惯的改善.然而目前学生数学学习中的低效表现呼唤高效数学学习方法.

1 数学学习中的低效表现

很多学生认为学习数学就是解题,解一道一道的具体题目.学生每天在书山题海中跋涉,做了大量的题目.说做题甚至都已经过时了,应该叫“刷题”(据说有的学校高中三年仅数学试卷摞起来竟达280cm 高).然而在很多情况下,学生的做题数量与取得的成绩是不相匹配的.经常听到家长说“孩子每天都熬夜到很晚,用了大量的时间做数学作业可是数学成绩仍鲜有提高”.很多学生,老师讲时也能明白,做过的题目过几天就忘了,于是反复练、重复练就成了家常便饭.经常听到老师们抱怨“这个题讲了n遍了,还是这么多学生出错”.种种迹象表明很多学生的数学学习是低效率的.

2 数学学习效率低的成因分析

美国数学家哈尔莫斯认为,问题是数学的心脏,数学的真正组成部分是问题和解.数学问题是数学学习的基本要素,学习数学就是“问题解决”, 而数学题是数学问题的一个载体,是数学问题的具体呈现.学习数学离不开解题,著名数学家华罗庚曾说过“学习数学不做题如入宝山而空手归”.但是如果解题只是就题论题、浅尝辄止,而看不到题目所蕴含的数学本质,面对稍微灵活一点的题目便会无所适从.究其原因是因为学生缺乏问题意识,仅靠多做题,只是就题论题,这种数学学习总是碎片化的,是缺乏逻辑性和系统性的,也一定是低效能的,因为没有整体系统的知识是容易丢失的,没有逻辑关联的知识是容易偏离的.

例1已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1 与该椭圆相交于A、B两点,且满足OA⊥OB,求椭圆的方程.

例2已知直线l过点且与椭圆相交于C、D两点,求证以CD为直径的圆过定点E(1,0).

例3已知椭圆= 1 外一点M(m,0)(m ＞倾斜角为的直线l交椭圆于C、D两点, 若点N(3,0)在以线段CD为直径的圆E的外部,求m的取值范围.

例4已知直线l过点且与椭圆相交于C、D两点,试问: 在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T? 若存在,求出点T的坐标;若不存在,请说明理由.

以上4 个题目都是围绕同一个问题编拟的, 即“垂直问题”.例1 设A(x1,y1),B(x2,y2) 根据OA⊥OB列出x1x2+y1y2= 0 而解答.例2 以CD为直径的圆过定点E,实质上还是EC⊥ED.例3 点N在以线段CD为直径的圆E的外部,等价于例4 与例2 的区别就是例2 中点E的坐标是已知的,而点T的坐标是未知的,理解到这一点,只要能求出点T的坐标(比如运用特殊值法)剩下的就应该与例2 相同了.尽管4 道题目围绕同一个问题,且题目与题目之间仅仅是细微的变化,但就是这每一次的细微变化,都会阻碍一些学生的脚步.由于4 道题目学生不会同时遇到,如果学习仅仅就题论题、碎片化的,等遇到后面的题目时前面的题目就已经忘记了,老师的每一次讲解都要另起炉灶、重新开始.即便是4 道题目全部做过,由于4 道题目分别在不同时段,且没有很好的整合,也很难认识到这类题目的本质规律.也就是说学生学习效率低的原因是在很大程度上是没有很好的发挥已做题目的作用.

3 “问题·账户·系统”学习法

“问题·账户·系统”学习法是指学生在数学学习过程中,从数学问题及其解法或者是定理、性质、结论等提炼出一般性的数学问题中,建立一个属于该一般性数学问题的账户,在后续的学习中围绕这一问题逐步进行积累、建构、进而形成一个完善的数学问题系统的数学学习方法.“问题·账户·系统”学习法有提炼问题、建立账户、积累构建、形成系统几大基本步骤.

“问题·账户·系统”学习法遵循建构主义原理,通过给数学问题建立账户的形式,不断积累与建构数学问题,逐步形成数学问题系统.完善的数学问题系统的形成意味着能从数学问题千变万化的具体呈现中洞察其来龙去脉、把握其本质规律.“问题·账户·系统”学习法强调在原有知识体系的基础上构建,重视旧知与新知的整合,最大限度的发挥已做题目的作用,真正做到“经历+总结=提高”,进而提高解题效率.

例1-例4 仅仅是“垂直问题”的几个变式而已,其实关于垂直问题的变式还有很多,如果每遇到一次变式,就把这一问题补充完善、梳理整合,积累到一定程度,认识到这类问题的本质规律也就是水到渠成的事了.

4 “问题·账户·系统”学习法的实施

4.1 提炼问题、建立账户

学习数学要有问题意识,要善于发现问题、提出问题、提炼问题,只有提炼出问题才有可能给所提炼的问题建立一个“账户”.也只有给问题建立起一个账户,才能围绕这一问题逐步进行构建,逐步存储一些有价值的东西.这就和银行存款一样,只有在银行建立一个账户,才能不断向这一账户存款.如果没有问题意识、账户意识,那么学习数学就只剩下解题了.

前文所述,如果解答例1 时就给垂直问题建立一个账户,解答例2-例4 时及时积累关于垂直问题的一些变式,那么就会对这一问题的认识越来越深刻,积累到一定程度,就会出现任其垂直问题千变万化总能透过现象看到本质的东西.再看下面的例子.

例5若0＜a ＜1,且函数f(x) =|logax|,则下列各式中成立的是

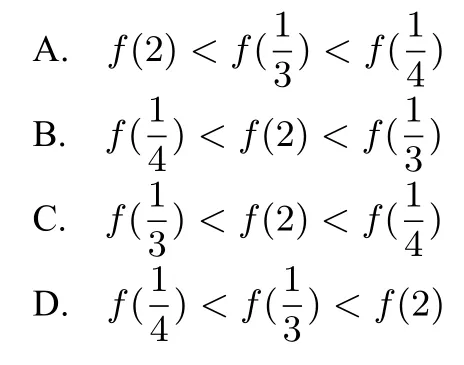
这是课本上的一道传统题目,运用数形结合(如图1),其本质就是f(a)=f(b),则ab=1.答案选A.

如果解答此题仅是就题论题,求解之后没有做过多思考,也没有进一步提炼出这道题目所涉及到的问题,那么解此题的效率就很低了.

例6(2010 高考全国新课标Ⅰ卷理科第10 题)已知函数f(x) =|lgx|,若0＜a ＜b,且f(a) =f(b),则a+2b的取值范围是

例7设方程3x=|lg(−x)|的两个根为x1,x2,则

A.x1x2＜0 B.x1x2=0 C.x1x2＞1 D.0＜x1x2＜1

例8已知函数f(x) =若0＜a ＜b ＜c,满足f(a) =f(b) =f(c),则的取值范围是_____.

分析对于例6,不难得到a+2b=a+然后再利用“对勾”函数的性质, 可得出答案选C.对于例7, 如图2, 此题就是在原来例5 的基础上进行了一些变化,但是无论如何变化,只需抓住y=|ln(−x)|的性质,就能体会变中的不变,答案选D.对于例8,只要理解好f(x)=|logax|(a ＞0,a/=1)的性质,就能得到ab= 1,然后只需求出的范围即可,答案为(1,2).

如果学生第一次遇到例5 时, 就提炼出函数f(x) =|logax|(a ＞0,a/=1)的性质,并及时给这一问题建立一个账户,在以后的学习中再碰到诸如例6-例8 中的问题,及时进行补充、完善,把前后问题整合在一起,那么这种学习就是围绕问题在学习.如果围绕这一问题不断积累,就会发生有量变到质变的飞跃,这就是我们经常所说的厚积薄发.

4.2 积累建构、形成系统

提炼问题、建立账户后,根据学习的进展,要逐步补充完善,每一个问题要有足够的题目或变式作为支撑,也就是说这个问题要有一个基本骨架,有了这样一个基本骨架,才叫有了“形”,进而形成一个有血有肉的有机整体,形成一个数学问题系统.尽管说问题和具体题目不是一回事,但是问题还需要具体题目来呈现.

例如前面围绕函数f(x) =|logax|(a ＞0,a /= 1)的性质所建立的账户,尽管存储了诸如例5-例8 等题目后已经不再是干巴巴的性质而是有血有肉的一个小的单元,或着具有了一个“雏形”,但仅有这几个题目还不足以支撑起这一问题的整个系统.

例9已知函数f(x)=若0＜x1＜x2＜x3, 满足f(x1) =f(x2) =f(x3), 则的取值范围是____.

例10已知函数f(x)=若−1＜a ＜b ＜c ＜d,满足f(a) =f(b) =f(c) =f(d),则a+b+c+d的取值范围是____.

例11(2018年全国高中数学联赛(B) 一试第10 题) 已知定义在(0,+∞) 上的函数f(x) 为f(x) =设a,b,c是三个不相等的实数,满足f(a)=f(b)=f(c),求abc的取值范围.

分析例9 就是把例8 中的函数进行了平移,由此变成了(x1+1)(x2+1)=1.理解了此种变化问题就不难解决了,答案仍为(1,2).例10 是把例9 中的分式函数变成了二次函数,(a+1)(b+1) = 1,c+d= 4,就可以求出a+b+c+d的取值范围是(4,+∞).例11 就是把函数y= log3x平移和翻折变换,此时f(a) =f(b)已不再是a,b互为倒数,而是ab=32=9,但本质上还是一样的,其具体解法如下:

解不妨设a ＜b ＜c, 则a ∈(0,3),b ∈(3,9),c ∈(9,+∞), 因为f(a) =f(b), 1−log3a= log3b −1, 所以ab=32=9,于是abc=9c.又因为0＜f(c)=4−所以c ∈(9,16),故abc ∈(81,144).

例5-例11 尽管都属于“函数f(x) =|logax|(a ＞0,a /=1)的性质”问题.题目考查点各有侧重,难度也各有不同,有课本题目、也有高考试题,还包括竞赛题目,但归根结底都与函数f(x) =|logax|(a ＞0,a /= 1)的性质有关.如果说例5-例8 是这一问题的雏形,积累到例9-例11,就构建起了一个比较完善的系统了.如果构建起了这样一个系统,那么学生对这一问题的认识就不会再是就题论题了,就能从千变万化中洞察和把握其中的本质规律.我们经常说题目万变不离其宗,此时学生就能够抓住这个宗.这类问题的宗就是无论题目怎么变化,都要围绕函数f(x) =|logax|(a ＞0,a /= 1)在“区间(0,1)上单调递减,在区间(1,+∞)上单调递增”以及的本质.当然题目变化之后,这一本质也会出现一些新的呈现方式(例如例9 中变成(a+1)(b+1)=1,例11 中f(a) =f(b)变为ab= 9),但是无论如何变化,都是围绕这一性质的变化.如果学生能抓住这一点,千变万化的一道一道的具体题目呈现在面前时,就能够不畏浮云遮望眼了,甚至学生都可以自己编题了.

当然不可否认,某些数学天分极高的学生在例5 的基础上就能直接上升到例11 的问题,甚至是有能力直接解答例11,但是据笔者多年的教学实践,如果仅仅是给问题建立了账户,而围绕问题的积累还非常单薄,还不具备足以构建起支撑起这一问题基本变化系统,还是不能游刃有余的解决此类问题的.任何一个问题系统都有构成这一问题系统的基本要素,也就是说这个系统应包含这类问题数学本质、以及数学本质的具体呈现形式,处理这一类问题的基本规律、技巧,以及学生在解决这类问题中容易出现的错误等等都属于这个问题系统的构成要素.当然构建起的系统也不是内容越多越好,整个建构过程应该是一个去粗取精、去伪存真的过程,也是一个因人而异的过程.“问题·账户·系统”学习法是要给所有的(既包括天分极高、也包括看似天分不高的)学生提供一种知识梳理与盘点的学习方法,只是面对同一问题,其梳理与积累的方法和耗费的精力因人而异罢了.

也许有人说,为什么老师讲解例5 时不把这些变换给学生讲清楚呢? 事实上,由于受时间、课时,以及学生接受能力的限制,围绕这一问题的诸多题目是不可能一下子给学生呈现的,因为这也违背了分层递进、螺旋上升的认知规律,以及够一够摘桃子的“最近发展区”理论.整个积累完善的过程应该是先由教师引导,最终要变成一个学生的自发行为.目的是让学生掌握一种梳理知识、总结反思的学习方法.另一方面如果仅仅看到问题的“终点”或是较高目标点,而忽视数学问题系统的构建过程结果也会适得其反.

例12(2012年高考山东卷理科第21 题) 已知函数(k为常数,e=2.71828···是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.

(1)求k的值;

(2)求f(x)的单调区间;

(3)设g(x) = (x2+x)f′(x),其中f′(x)为f(x)的导函数.证明: 对任意x ＞0,g(x)＜1+e−2.

分析例12 是2012年山东高考理科的压轴题,当时得分率很低,特别是(3)更是很少有考生问津,更不用说得分了.(3)实际上就是要证明当x ＞0 时,1 + e−2.而要完成此不等式的证明很多考生就会无所适从, 但是只要熟悉不等式“ex ＞ x+ 1(x ＞0) ”就可把不等式变形为(1−x −xlnx)＜1 + e−2, 而只需证明1−x −xlnx≤ 1 + e−2,或者说只需求出h(x) = 1−x −xlnx(x ＞0) 的最大值就可以了, 这就把压轴题变成一个十分简单的问题了.其实此题就是表达式的“变形与转化”问题中的一种情况,如果不把这种情况纳入到整个“变形与转化”系统中,按照由浅入深的原则进行积累与建构,即便是老师讲过了,再遇到类似问题学生还会无所适从.这就是老师们经常抱怨的“这种题该会的不讲也会,不会的讲了也不会”.一个主要原因是作为老师没有关于“变形与转化”的问题系统,更没有引导学生逐步积累与建构的意识,只是把目标定位在了问题的较高目标点.

5 “问题·账户·系统”学习法的成效

案例1课堂教学中笔者曾结合某些高考或模拟题讲过抛物线一个常用性质.有个名叫关乐萌的同学运用“问题·账户·系统”学习法,对此类问题不断积累、不断完善,完成了论文《一个久考不衰的抛物线的性质》.

案例2一次老师课堂上讲到巧妙利用对称性使圆锥曲线题目不再困难.一个名叫孔湛琦的同学对圆锥曲线中对称性的应用进行了积累和梳理,完成了《用对称性求解圆锥曲线高考题》.

案例3课堂教学中笔者讲过向量的拆分技巧.一个名叫朱静怡的同学在笔者所讲例题的基础上不断积累、拓展最后完成了论文《关于高中数学学习中万变向量的拆分》.

以上几个案例只是众多案例的几个典型代表,笔者的很多学生作品或发表于各类报刊、杂志,或在各级各类比赛中获奖.新课程已经将数学探究、数学论文写作提高到非常重要的地位,有很多教师还在为评职晋级没有论文发表而焦急的时候,我们的学生竟能在一些重要期刊上发表自己的论文,这不能不说这些学生掌握了一种高效的学习方法.每当看到自己学生的作品发表或获奖,心里都有一种溢于言表的自豪和幸福感.笔者感到高兴的绝不仅仅是学生取得的成绩,更重要的是看到学生已经掌握了一种行之有效的高效学习方法,真正实现了授人以鱼不如授人以渔.