夹逼法则在中学数学解题中的应用*

广东省中山市中山纪念中学(528454) 李文东

高等数学中的夹逼法则主要用来求极限,在初等数学中,我们也可以借助这一思想来解题.夹逼法则的常见模式如下:设g(x)≤f(x)≤h(x),若存在x0,使得g(x0)=h(x0)=m,则必有f(x0) =m.一些常见的特殊情况有: 设a ∈R, 若有a2≤0, 因为a2≥0, 则a= 0; 在三角函数中, 若有sⅰnα≥1(sⅰnx≤−1),因为−1 ≤sⅰnα≤1,则有sⅰnα= 1(sⅰnx=−1),下面举例说明夹逼法则在中学数学解题中的运用.

一、夹逼法则在三角函数中的应用

例1在ΔABC中,若cos(A −B) =证明:A+B=

解由题意易知cos(A −B)＞0,且

从而cos(A+B)=cos(A −B)[1−sⅰn(A+B)]≥0,于是A+B≤又

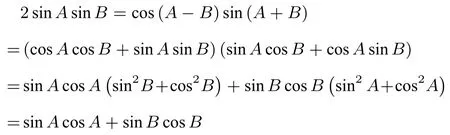
点评本题是一道难题, 先通过cos(A+B) ≥0 得到A+B≤然后通过y=sⅰnx的单调性构造出夹逼法则模式来证明A+B=

例2设α,β ∈

且 满 足cosα+ cosβ −求证:α=β=

证明由题意: (1−cosβ)cosα −sⅰnβsⅰnα+cosβ −= 0, 令cosα=x,sⅰnα=y, 则x2+y2= 1 且(1−cosβ)x−ysⅰnβ+cosβ−=0,即直线(1−cosβ)x−ysⅰnβ+cosβ−=0 与圆x2+y2=1 有交点,故圆心到直线的距离又≥0, 故cosβ=此时cosα=又,故α=β=

点评一个等式含有两个变量α,β,一般来说很难求出α,β.这里通过数形结合的思想构造出夹逼法则是求解的问题的关键.

例3在ΔABC中,A,B,C所对的边分别为a,b,c,若a2=3b2+3c2−则C=____.

解由余弦定理:a2= 3b2+ 3c2−b2+c2−2bccosA,根据基本不等式有b2+c2=bccosA=故=1,得A=此时b=c,从而C=

例4在ΔABC中,A,B,C所对的边分别为a,b,c,若a= 1,−sⅰn2A= sⅰnAsⅰnBsⅰnC, 求ΔABC面积的最大值.

解由正弦定理得:=bcsⅰnA,又根据余弦定理b2+c2−a2= 2bccosA,两式相减得:bcsⅰnA −2bccosA,由基本不等式于是bcsⅰnA −2bccosA≥从而sⅰnA −2 cosA≥即其中cosφ=因此sⅰn(A −φ) ≥1,又sⅰn(A −φ) ≤1,故sⅰn(A −φ) = 1,即sⅰnA −2 cosA=于是sⅰnA=而b2+c2−1 =≥2bc −1⇒bc≤于是即ΔABC面积的最大值为

点评以上两例都是运用基本不等式来产生出夹逼法则的模型,其实就是由等式如何构造出合适的不等式问题,仔细观察题中所给的等式的结构是关键.

二、夹逼法则在函数求值和求表达式中的应用

例5设二次函数f(x)=x2+bx+c,已知不论α,β为何实数恒有f(sⅰnα)≥0 和f(2+cosβ)≤0,求证:b+c=−1.

证明因为sⅰnα ∈[−1,1],2+cosβ ∈[1,3],由题意知:当x ∈[−1,1]时,f(x) ≥0,从而f(1) ≥0;当x ∈[1,3]时,f(x)≤0,从而f(1)≤0,于是f(1)=0,即1+b+c=0 得b+c=−1.

例6已知二次函数f(x) =ax2+bx+c的图象过点(−1,0), 问是否存在常数a、b、c, 使不等式x≤f(x) ≤对一切x ∈R 都成立?

解由题意:f(−1) =a −b+c= 0, 在x≤f(x) ≤中令x= 1 得: 1 ≤f(1) ≤1,从而f(1) = 1,即a+b+c= 1,与a −b+c= 0 联立得故f(x) =−a, 又不等式f(x) ≥x恒成立, 即ax2−−a≥ 0 恒成立, 于是a ＞0 且≤0, 即(4a −1)2≤0⇒a=于是f(x)=

点评在条件x≤f(x) ≤中怎么想到取x=1,我们只需要令x=(1+x2)解出x=1 即可.

例7已知t为常数,函数f(x) =x2−2x −t在区间[0,3]上的最大值为2,则t=____.

解由于函数y=x2−2x −t的对称轴为x=1∈[0,3], 故fmax(x)∈max{f(0),f(1),f(3)}= 2, 从而故t=1.

点评题目提示我们t的值唯一确定,通过对f(x)的最大值的可能性来确定缩小t的范围而求出t的值.

例8设定义在R 上的函数f(x),若f(0)=1 对任意的x,y都有f(x+2)−f(x)≤3·2x,f(x+6)−f(x)≥63·2x,则f(2016)=____.

解由题意有:f(x+2)≤3·2x+f(x),于是

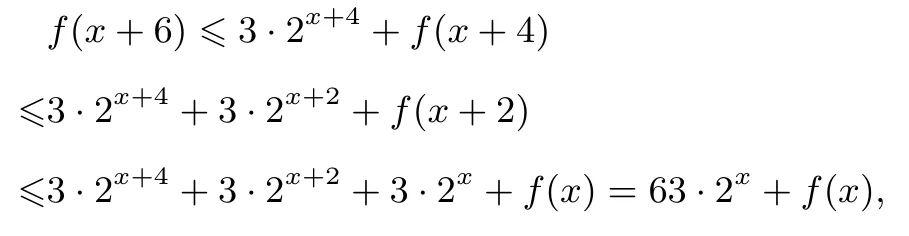
从而f(x) + 63·2x≤f(x+ 6) ≤f(x) + 63·2x, 故f(x+6)−f(x)=63·2x.f(6)−f(0)=63·20,f(12)−f(6)=63·26,··· ,f(2016)−f(2010) = 63·22010, 将以上等 式相加得:f(2016)−f(0) = 63·(20+26+···+22010)==22016−1,于是f(2016)=22016.

例9定义在R 上的函数f(x)满足条件f(x)+f(1−且f(0) = 0, 当0 ≤x1＜x2≤1时,f(x1)≤f(x2),则=____.

解在f(x)+f(1−x) = 1 中分别令x= 0 和x=可得:f(1)=1,中令x=1得:又当0 ≤x1＜x2≤1 时,f(x1) ≤f(x2),故x ∈时,f(x) =同理, 当x ∈时, 则于是即x ∈时,f(x) =按照这种做法继续下去可得: 当x ∈时,f(x)=.而当n=7 时,于是选B.

三、夹逼法则在恒成立问题中的应用

例10若实数x,y满足2x −3 ≤ ln(x+y+1) +ln(x −y −2),则xy=____.

解由于lnx≤x −1,等号当且仅当x= 1 时成立,故2x−3 ≤ln(x+y+1)+ln(x −y −2)≤x+y+x−y−3=2x −3, 于 是2x −3 = ln(x+y+1) + ln(x −y −2) 且x+y+ 1 = 1,x −y −2 = 1, 得x=故xy=

点评仔细观察条件后运用不等式lnx≤x −1 放缩是解决本题的关键.

例11若不等式ax−lnx≥a(2x−x2)对∀x ∈(0,+∞)恒成立,则a=____.

解由题意:a(x2−x)≥ lnx, 分离参数得: 当x ∈(0,1) 时,a≤从 而a≤当x ∈(1,+∞) 时,a≥从而a≥于是

点评本题是一道恒成立问题, 作为填空题, 它提示我们满足条件的a的值唯一确定, 分离参数后x ∈(0,1) 和x ∈(1,+∞)部分不等式方向相反,因此我们可以采用夹逼法则考虑x= 1 附近的值来迅速确定a,求a的值最后用了洛必达法则.

例12(2018 高考全国ⅠⅠⅠ卷第21 题)已知函数f(x) =(2+x+ax2)ln(x+1)−2x.

(1) 若a= 0, 证明: 当−1＜x ＜0 时,f(x)＜0; 当x ＞0 时,f(x)＞0;

(2)若x=0 是f(x)的极大值点,求a.

解(1)略.(2)由题意:

f′(x)=x= 0 是f(x) 的极大值点, 则存在充分接近于0 的δ, 使得当x ∈(−δ,0) 时,f′(x)＞0, 当x ∈(0,δ) 时,f′(x)＜0,对任意的x ∈(−1,+∞),都有2xln(x+1)＞0,进而有2xln(x+1) +＞0, 分离参数后有: 当x ∈(0,δ) 时,a ＜当x ∈(−δ,0) 时,从而根据洛必达法则有:

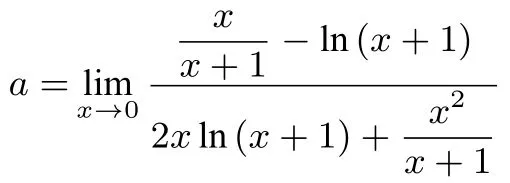
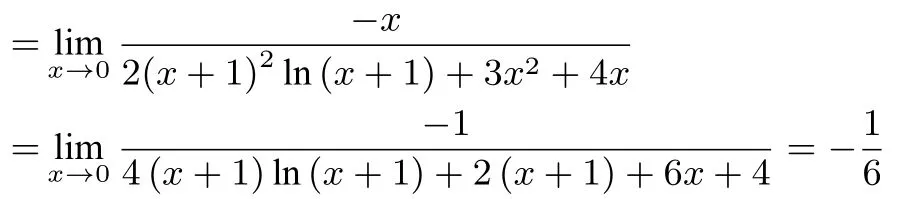
点评通过本题我们可以得到已知极值点求参数值问题的一般解法.以x=x0为函数f(x) 的极小值点为例, 且设f′(x0) = 0.根据极小值点的定义可知: 存在充分接近于x0的δ, 使得当x ∈(x0−δ,x0) 时,f′(x)＜0, 当x ∈(x0,x0+δ)时,f′(x)＞0.假设f′(x)经过变形后得到:当x ∈(x0−δ,x0)时,a·g(x)＜h(x); 当x ∈(x0,x0+δ)时,a · g(x)＞h(x).若当x ∈(x0−δ,x0)∪(x0,x0+δ)时, 有g(x)＞0(或g(x)＜0), 则 当x ∈(x0−δ,x0)时,a ＜而 当x ∈(x0,x0+δ) 时由于δ充分小, 故此时实数a的取值范围为:a=

借助夹逼法则解题,方法精巧,思路独特.它将不等与相等这对关系有力的统一起来,解题的关键是怎么样由等量关系产生不等关系,或者是根据不等关系得到等量关系,从而使得复杂的问题得到解决.