如何让核心素养在数学课堂上有效落地
——例说抛物线及其标准方程的教学
2021-04-16马德宇江苏省丰县中学221700
马德宇 (江苏省丰县中学 221700)
就数学学科而言,核心素养体现着数学学科的本质,具有普遍性,同时具有不可替代的育人价值.立足于提升核心素养,数学教学首先应当夯实学生的知识基础,引发学生的深度思维.文[1]提出数学认知的三个重要内容:数学理论的内化,数学技能的形成,数学经验、思想、观念的获得;并把这三个方面及其联系简化为“数学认知三角形”(图1).要确保数学课堂教学的有效实施,必须提高学生的智力参与程度,让他们亲身经历模式构建的过程.
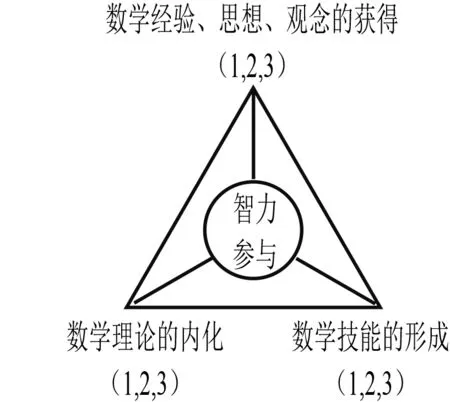
图1
1 课堂实录
1.1 探究规律,引入新课
师:请同学们回忆一下椭圆及双曲线的第二定义,然后以学习小组为单位交流一下,比一比,看哪个小组能够提出值得研究的新问题.
生1:当0
师:为什么不考虑e≤0的情况呢?
生2:因为e是两个距离之比,故不可能小于0,而e=0的情况作为特例已在学习椭圆的时候研究过.
师:非常好!谁能将条件e=1用文字描述一下?
生3:e=1 即指动点到定点的距离等于动点到定直线的距离.
师:这个动点的轨迹到底是什么呢?
学生们议论纷纷,有的说肯定是一条新的曲线,有的开始提笔演算着什么,还有的估计提前预习过,说是抛物线……教师打开电脑,学生的目光被吸引到大屏幕上.
师:屏幕中央有一个动点M、一个定点F、一条定直线l,左上角是两个度量值MF与MN(图2).我开始操作,请大家注意观察,拖动点M,你有什么发现?
生(众):MF及MN都在改变,但它们的长度总相等.
师:咱们追踪点M,同学们再看看有什么发现?(图3).
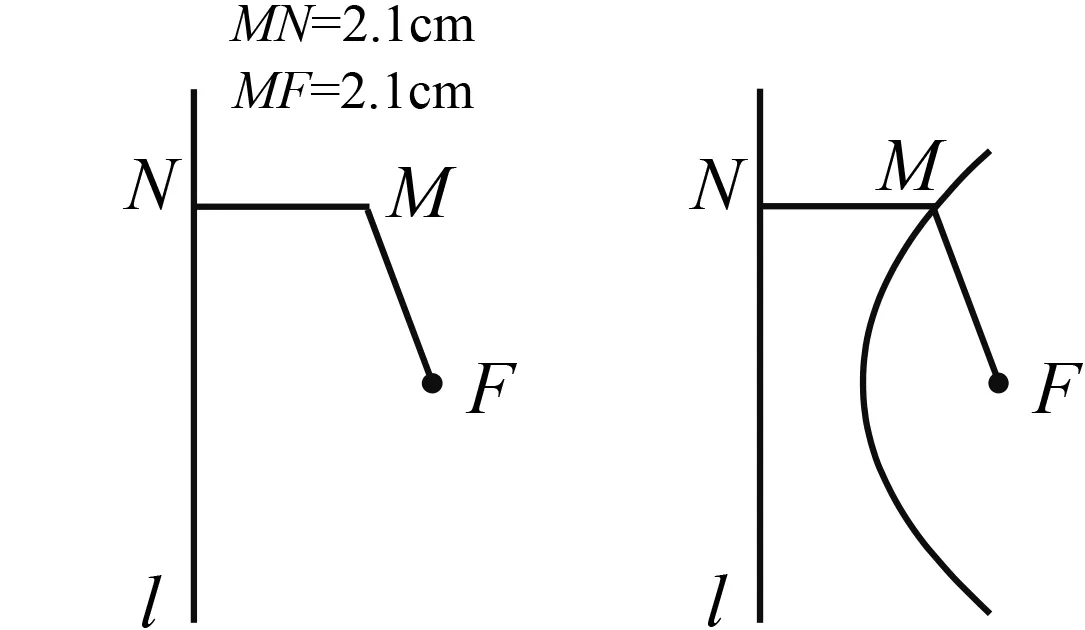
图2 图3
生(众):抛物线!
生4:不一定!也可能是双曲线的右支.
生5:不可能!因为双曲线上的点到定点的距离大于它到定直线的距离.
师:既然如此,咱们就把这支曲线叫做抛物线吧!但这仅是一个名称,我们能否给它下个科学的定义呢?
生(众):在平面内,到定点的距离等于到定直线的距离的动点的轨迹叫做抛物线,定点叫做抛物线的焦点,定直线叫做抛物线的准线.
1.2 合作交流,突破重难点
师:接下来该干什么呢?
生(众):求抛物线的标准方程.
(学生开始动手演算,生6突然举手)
师:你有什么发现?说出来让大家听听.
生6:在椭圆及双曲线的第二定义中,定点的坐标及定直线的方程是给定的,故不需要建立直角坐标,但这里该怎么办呢?
师:是呀,这里该怎样建立直角坐标系?
生7:因为点F和直线l分别是定点和定直线,所以点F到直线l的距离也应该是定值……
师:的确是这样.通常我们用字母p来表示这个定值,你准备怎么办?
生7:过点F作FK⊥l,垂足为K,并以KF所在直线为x轴,以点K为坐标原点建立直角坐标系.(部分学生点头认可)
生8:我也是这样选定的x轴,但我认为也可以选点F为坐标原点.(又有另一部分学生点头赞同)
生9:由抛物线定义可知,KF的中点也在曲线上,考虑到数学的对称美(学生们“哗”地大笑起来,因为这句话是我经常说的,想不到被生9借用了),我认为也可以选KF的中点为坐标原点.
师:大家先别争了.我们以学习班小组为单位,编号为A的用生7的方法,编号为B的用生8的方法,编号为C的用生9的方法,编号为D的自选一种方法.3分钟后以小组为单位进行交流讨论,然后咱们进行成果展示.
(3分钟之后)
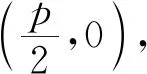
师:太棒了!谁来设计一道题?
生11:求抛物线y2=x的焦点坐标和准线方程.
1.3 引领反思,类比再探
师:下面,咱们来一段“经典影片”回放:你们的脑海中是否曾经有过抛物线的踪影呢?
生13:初三时学过的二次函数y=ax2的图象好像也叫做抛物线.
师:不是好像,而是肯定!那么,此抛物线与彼抛物线有何区别和联系呢?
生14:图形关于直线y=x对称.
师:太棒了!我们能否将抛物线在y2=2px(p>0)的基础上作一些必要的拓展呢?(学生思考3分钟之后)请同学们将大屏幕上展示的表1补充完整,并力争使自己头脑中的知识条理化、系统化.
1.4 简单应用,巩固新知
师:编几道题怎么样?

表1
生16:求抛物线y=ax2(a≠0)的焦点坐标与准线方程.
生17:芦沟桥的桥洞好像也呈抛物线型,我们也许可以从数学的角度设计几个关于芦沟桥的问题……(下课铃响了,有的学生略显遗憾)
师:同学们可以在课后继续讨论,下节数学课我们接着交流.
2 课后反思
2.1 教学特点
上面的教学过程具有如下几个特点:(1)抛物线及其标准方程用的是概念同化的方式.新概念的固着点是原有的椭圆与双曲线的理论.这不仅为新知识的内化找到了合适的固着点,而且使旧知识在新课的运用中得到巩固和发展.注重类比迁移,培养学生的推理能力.(2)在新课的设计中, 把抛物线的概念及其标准方程作为重点加以强化,抓住了抛物线的核心,对于提出和研究抛物线的性质做了较好的准备.注重了数形结合,培养了学生的模型思想.(3)学生积极参与教学活动,使得数学思维的训练此起彼伏,既放得开,又收得拢.这里的“放”与“收”都是在数学思想的指引下进行的.这对培养学生的数学意识是有益的.
2.2 教学体会
(1)学生只有通过自主探究学习,才会有深刻的感悟,在合作交流中有话可说,从而相互启发、相互借鉴、相互补充,迸发出绚丽多彩的创造火花.(2)学生是课堂的主人,学生能想的要让学生想,学生能做的要让学生做,学生能说的要让学生说.教师要给学生营造一个自主学习、勇于探索、合作交流的学习氛围.(3)学生的学习活动必须有足够的探索与交流的时间和空间.