基于建构主义数学学习观的“说数学”案例研究——以普通高中艺术特色学校为例*

吴荣燕 (广东省广州市美术中学 510060)

2020年10月中共中央、国务院印发的《深化新时代教育评价改革总体方案》(下称《总体方案》)指出：紧扣破除“唯分数、唯升学、唯文凭、唯论文、唯帽子”的顽瘴痼疾，立足基本国情，坚持积极、稳慎、务实，改进结果评价，强化过程评价，探索增值评价，健全综合评价．《普通高中数学课程标准(2017年版)》强调：评价不仅要关注学生对知识技能掌握的程度，还要更多地关注学生的思维过程，是否会用数学的语言表达世界．数学交流活动指在数学教与学过程中学生之间、教师与学生之间以提高数学交流能力为目的的活动，包括口头交流和书面交流两种形式．“说数学”是指个体用口头表达自己对数学问题的具体认识、理解,解决数学问题的思路、思想和方法以及数学学习情感、体会等的数学学习活动,是数学交流的重要形式之一.说数学可概括为“说知识”“说异见”“说过程”和“说体会”[1].

普通高中艺术特色学校是指招收和培养美术、音乐、舞蹈、传媒等专业方向的艺术生，以专业教学为办学特色，为艺术高校输送优秀生源的普通高中．以笔者任教的广州市美术中学为例，学生对专业学习有较高的主动性，但对文化课尤其是数学的学习缺乏自觉性．教师如何在数学教学中提高艺术生的数学口头交流能力，“说数学”活动能否激发其数学学习热情，这些问题值得深入研究．

1 案例呈现

笔者在讲授必修五“等差数列的前n项和(第1课时)”时，有一道练习题：已知数列{an}的前n项和Sn=2n2-3n(n∈N*)，则a4等于( ).

A.11 B.15 C.17 D.20

巡堂时发现不少学生都能较好地运用本节新授课的知识去解答，在讲评习题时先直接给出了常规解法：a4=S4-S3=(32-12)-(18-9)=11，然后询问学生还有没有其他的解法．由于平时我在课堂教学中经常鼓励学生大胆地“说数学”，这时生Y大胆举手说过程和知识．我一边请生Y走上讲台，一边将她的解答投影出来：

解法1 ①当n=1时，a1=S1=-1.

②当n≥2时，an=Sn-Sn-1=(2n2-3n)- [2(n-1)2-3(n-1)]=4n-5.

③经检验，当n=1时，an=4n-5也成立，故an=4n-5(n∈N*)．

因此a4=4×4-5=11.

生Y：这节课我们学了数列的前n项和与通项公式间的关系．已知Sn求an，就用这三步求解，得出数列通项公式后，可以求出数列任意一项的值．

师：很好，你觉得有哪些地方需要注意的吗？(激发学生“说体会”)

生Y：(补充)注意对通项公式的验证，就是当n=1时那个an的公式是否也成立．

在生Y说完后笔者及时进行了点评，表扬她的书面解答很好，非常规范，然后对她的“说”给予激励.

师：生Y的“说过程”和“说知识”都很不错，而且姿态大方，声音响亮，整个过程表述得非常清晰！

我原计划这道题讲到这里就结束了，突然，坐在教室后排的生L举手大声说：“老师，我有另一种解法，而且比生Y的更简便！”大部分的学生将目光移向生L，于是我请他上台分享，和全班同学一起听听他有什么新的“过程”．生L数学成绩中等，但思维比较活跃，他的解答如下：

解法2 因为a1=S1=-1，a2=S2-S1=3，所以d=a2-a1=4，故数列{an}的通项公式是an=a1+(n-1)d=4n-5，也可以算出a4等于11.

生L一说完，不少学生都惊呼这个方法非常好用，不用分两个步骤和验证了.但两三个反应快的学生说：“题目没说这是等差数列啊！”生L顿了一下说：“可我算的答案是对的啊！”看到学生们议论纷纷，情绪高涨，我又问：“生L的想法很好，得出的答案也是正确的，那么这个数列是不是等差数列呢？”生L在黑板上边演算边讲：“由生Y的解答，an= 4n-5(n∈N*)，a1=-1，a2=3,a3=7,a4=11，……且an-an-1=(4n-5)- [4(n-1)-5]=4，因此数列{an}是一个以-1为首项、4为公差的等差数列！”生L感到很高兴，我也对生L的积极发言给予鼓励.

师：生L敢于分享自己的解法，思路清晰，声音洪亮，很好！

师：如果我将题目稍稍改一下：已知数列{bn}的前n项和Tn=2n2-3n+1(n∈N*)，求bn呢？

(生L回到座位上，和同学们一起验算起来)

计算能力较强、平时不大爱说话、很少回答问题的女生Q主动举手展示了她的验算.

(生Q一气说完，有些脸红)

师：生Q的验算既快又准，并且分析得很好！确实如此，我在前n项和的式子后面加了个“1”，对应的数列就不再是等差数列了．

生L也陷入了沉思，提出了他的疑问：“有什么方法可以直接从前n项和Sn来判断一个数列是不是等差数列？”我对生L的大胆提问表示赞赏：“生L问得很好！同学们找找前面计算过的等差数列的通项公式和前n项和公式，观察一下an，Sn和n都有怎样的函数关系？请大家继续思考！”

过了几分钟，学生E分享她的看法.

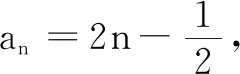
师：非常棒！生E找到了一些具体的数列，从一次函数、二次函数的角度解释了通项公式、前n项和公式的特征！

又过了两分钟，思维敏捷、数学成绩较好的数学课代表生F主动举手跃跃欲试．

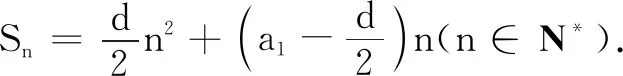
生F：(顿了一下，很惊喜)且常数项为零！

(学生们报以热烈的掌声)

师：非常厉害！生F能对等差数列的相关公式进行化简，进一步概括了等差数列的函数特性，表明他有很强的数学观察能力和探究能力，值得大家学习！

生L也很兴奋地再次举手，我示意让他来“说体会”.

生L：我明白了！练习题中的数列前n项和是一个关于n的二次函数且常数项为零，所以这个数列实际上就是一个等差数列，用我那个“简便”方法还是可以的．而老师给的变式，从前n项和的形式可以判断出这不是等差数列，就要用生Y的解法1规范解答．当然如果题目没有问通项公式，我们可以直接用an=Sn-Sn-1(n∈N*,n≥2)求解某一项的值．谢谢大家！

(学生们一边笑一边鼓掌，每个人都有收获)

这道练习题引申出来的“说数学”活动使得讲评的时间增加了近20分钟，导致原本的教学计划没有完成．

2 分析与讨论

以下从建构主义数学学习观出发，探讨在普通高中艺术特色学校开展“说数学”实践研究的教学策略．

(1)教师需搭建“说数学”的平台，成为艺术生数学学习活动的促进者

建构主义认为，学习是学习者的主动建构而非客观知识的被动接受.因此教师不应被看成“知识的授予者”，而应成为学生学习活动的促进者，应当努力调动学生学习的积极性．教师对于学生情况的了解事实上也是一个建构的过程，我们绝不应以自己的主观分析去代替学生的真实情况[2]．艺术生往往认为数学对专业学习起不到什么帮助作用，觉得数学枯燥无味，难以体会到学习数学带来的成功感．“说数学”属于“出声思维”模式，是传统的纸笔测验评价的有效补充.学生在主动构建论据与他人交流的同时逐步形成良好的数学素养[3].教师在课堂上开展“说数学”活动，对艺术生的数学学习会有积极的促进作用．

首先，“说数学”充分暴露了艺术生的思维过程，为教师获取了更及时的教学反馈．如果没有教师一直营造宽松、开放的课堂氛围，鼓励学生敢说敢疑，生L很难有机会或有胆量说出他错误的“简便方法”.教师通过“一言堂”顺利完成教学任务，却不知学生的思维中还暗藏着由等差数列产生的负迁移．

其次，教师给予的激励性评价提高了艺术学生学习数学的热情．在上述案例中，生L并不是一位成绩十分优秀的学生，在课堂练习中一开始也经历了艰难的解题过程，他主动向同学们“说过程”，在同学的“说异见”中苦苦思索自己的方法是否正确，在教师的举例和生F的证明中找到已知数列前n项和Sn去求an的一系列方法并“说体会”，其勇于表达、认真总结的精神得到了教师的高度赞扬和同学们的鼓掌激励．教师要重视通过“说数学”活动，加强对艺术生数学学习的明确知识和默会知识的评价，克服传统教学多重视明确知识而少关注默会知识的不足，多角度提高艺术生数学学习的自我效能感．

再次，教师可以将艺术生“说数学”的表现纳入学习综合素质评价之中．《总体方案》提出，深化新时代教育评价改革的重点任务是“改进结果评价，强化过程评价，探索增值评价，健全综合评价”．面对基础薄弱的艺术生，教师更应注重数学学习评价的多元性，更多地关注学生的平时表现、学习态度以及学习前后发生的变化.“说数学”是传统的测试成绩评价的有效补充，教师可将学生在“说数学”的表现纳入其学习综合素质评价之中．不论解题的结果是正确还是错误，生Y、生F在“说数学”的过程中所展现出的语言流畅、认真倾听、乐观自信，生L在数学问题解决困境中的不断尝试、善于追问和批判质疑等，都是他们在数学学习中形成的积极向上的情感、态度与价值观.

总之，教师需通过学生在“说数学”中展现出来的真实思维过程，研究学生已有的数学知识和活动经验在新的学习活动中的作用，在课堂中落实教育评价的革新理念，促进艺术生数学学习活动的有效开展．

(2)在艺术生“说数学”的过程中，教师应充分发挥“组织者”和“引领者”的作用

数学学习活动的一个重要特征就是“顺应”的过程，即认知框架的不断扩展或重组，后者也就是新的学习活动与主体原有的认知结构相互作用的结果．就数学教学而言，我们应更为明确地去提倡“数学地交流和互动”:教师应通过适当的提问和举例以促进学生反思，使学生清楚地认识到已有的方法和结论的不足之处，并使得相应的“优化”真正成为学生的自觉行为[2].对于数学基础薄弱、学习精力投入不足的艺术生来说，数学教师的主导作用显得尤为重要．

上述案例中，在教师的引导和学生的积极交流下，生L的认知结构的发展得到了非常详细的展示．一开始，生L依据在新的学习活动中学到的an=Sn-Sn-1(n≥2)和已有的对等差数列的认知d=an-an-1(n≥2)与an=a1+(n-1)d，认为通过练习中给的Sn可以求出a1和a2，进而求出d和an，表明生L善于将自身的“已有知识和经验”与教师授予的“新的学习内容”产生建构(即为“主动建构”)．教师并未直接地否定学生的解答，而是认真努力地去理解错误解答背后的合理性：可能是由于新的内容没有很好地得到消化，从而与已有的知识或经验产生冲突．若此时生L不能感受到冲突，则需要教师去“制造”这个认知冲突，“组织”学生进行自我反省．学生的“说异见”和教师设置的变式促使生L开始对两种解题思路进行比较,他的“说体会”实质上就是新的认知结构对于已有的认知结构的顺应和取代．

当学生在认知框架不断扩展或重组中遇到困难，不能自觉地去设定探索目标时，教师在学习活动中就必须成为“引领者”，否则学生的主动建构容易发展成一个十分漫长和事倍功半的过程．例如，当学生在探索如何根据数列前n项和Sn判断数列是否为等差数列时，教师没有充当从天而降的“救世主”，而是给予学生必要的导向：可以先从一些具体的数列实例出发，观察an和n之间、Sn和n之间的函数关系，再从公式上研究其中的一般规律，明确进一步努力的方向．

可见，数学教师在教学中需要发挥“教练”的作用，通过适当的提问、举例、示范等，促使艺术生在“说数学”中自觉地完成相对独立的建构活动，提高艺术生的元认知能力．

(3)教师需重视“说数学”对创建学习共同体的价值

“数学学习共同体”就是在一个教学班中，为了促进学生数学知识的增长和数学能力的提高，以及使学生形成一定的情感、态度和价值观，教师和学生结合成一个数学学习的团体[4]．学习并非是孤立的个人行为，而是学习共同体的共同行为．教师的一个重要责任，即为学生的学习创造良好的环境，包括努力培养出一个好的学习共同体[2]．

“说数学”活动强调每个成员的积极参与，促成整个班级在此过程中形成规范．“说者”要学习如何姿态大方、声音响亮、有条有理地说；“听者”要学会认真倾听，尊重他人，谦虚地提出自己的“异见”；教师需要营造民主和谐的课堂，把学生视为学习的主体，在学生的“说”当中发挥主导作用．再者，“说数学”活动强调了学习共同体不同成员间的积极合作，为学习成果的共享搭建了平台．任何真正的数学认识活动都必须是主体的主动建构，因此学生在认知上存在着个体特殊性．在讨论an,Sn和n之间的函数关系时，成绩中等、积极互动的生E最先从一些具体的数列例子中找到关联；思维敏捷的生F善于从抽象的公式中提炼出an,Sn与自变量n的函数关系式；然后由乐于总结的生L来进行归纳，展现出“不同的学生学到不同的数学”．最后，相对于传统的课堂中的教师问、学生答，回答正确与否由教师判定，“说数学”活动促进了个体之间的数学语言表述、交流、批评和自觉反思，使得数学学习共同体中的每个个体保持思维的开放性．学生判断真理的依据也不是教师的意见，而是理性的思考．

因此，“说数学”活动能够优化艺术生数学课堂教学环节，有效提高艺术生数学交流能力，在创建积极良好的艺术生数学学习共同体上有着重要的价值．

我国的教育发展正走入新时代，教师需对自身的数学观和教学观保持自觉反省与必要更新．以上基于建构主义数学学习观，对普通高中艺术特色学校的“说数学”活动展开案例探究，得出了一些结论．在新课改的背景下，“说数学”对于培育艺术生的核心素养具有怎样的作用，还有待进一步的研究．